Chebyshev多项式在PPP卫星钟内插计算中的应用研究

杨怀义，杨兴跃，王 帅

(1.中国建筑材料工业地质勘查中心山西总队，山西 太原 030000； 2.南阳市城乡规划测绘院，河南 南阳 473000)



Chebyshev多项式在PPP卫星钟内插计算中的应用研究

杨怀义1，杨兴跃2，王 帅2

(1.中国建筑材料工业地质勘查中心山西总队，山西 太原 030000； 2.南阳市城乡规划测绘院，河南 南阳 473000)

在精密单点定位中，卫星星历、观测值和卫星钟钟差需要达到时间上的同步。运用Chebyshev多项式对卫星钟差产品进行内插计算。4～10阶Chebyshev多项式内插结果可以达到亚纳秒级别，且9阶时精度最高，然后将内插结果应用到精密单点定位中。实验结果表明：利用Chebyshev多项式内插计算得到的钟差产品可以满足精密单点定位的需要。

精密单点定位；卫星钟差；Chebyshev多项式

卫星钟的钟误差和光速的乘积会对定位结果产生较大的影响，这是因为光速较大，每秒可以传播约3×105km[1]。因此对卫星钟误差需要慎重考虑并加以控制。在精密单点定位中，目前采用的策略大多是利用IGS发布的精密卫星钟钟差产品降低误差影响[2-3]。IGS发布的卫星钟差产品包括预报和事后钟差两种产品[4]，其中事后钟差中5 min间隔和30 s间隔的产品都可以满足精密单点定位的需要。但观测值的采样间隔大部分为30 s，甚至更密。卫星钟钟差产品需要和观测值在采样间隔上达到同步[5]，这需要内插一些间隔较大的钟差数据。

1 Chebyshev多项式拟合的数学模型

由于Chebyshev多项式适用于[-1,1]的区间，因此在进行星历拟合时要先对插值区间进行转化。在[t0,t0+Δt]内采用n阶Chebyshev多项式拟合时，完成转化的计算公式为

(1)

卫星坐标可以表示为

(2)

式中Ci为Chebyshev多项式的待求的未知系数。

利用递推关系

T0(τ)=1

T1(τ)=τ

(3)

在拟合时间[t0,t0+Δt]中选取m(m>n+1)个点，由式(2)可得m个时刻的拟合坐标x，将拟合坐标x和已知坐标X求差可得

Vm×1=xm×1-Xm×1

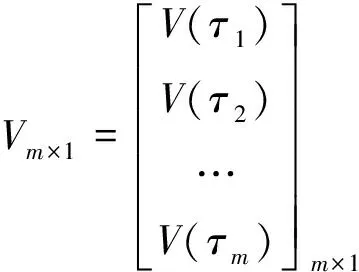
(4)

x=BC

(5)

式中B是T的m×n阶矩阵。

根据最小二乘法原理可知C=N-1BTPX，其中N=BTPB[6]。将求得的C代入式(2)，即可求出任意时刻的GPS卫星的坐标。

根据Chebyshev多项式Tn(τ)结构，可以看出在区间[-1,1]上多项式的曲线和Y轴的交点有n个，即n个零点：

(6)

和n+1个极值点:

(7)

这两组点称为切比雪夫点，它们是单位圆上等距分布点的横坐标，即插值区间的中点相互对称[7-8]。利用切比雪夫点插值，可以使插值区间的最大偏差达到最小[9-10]。

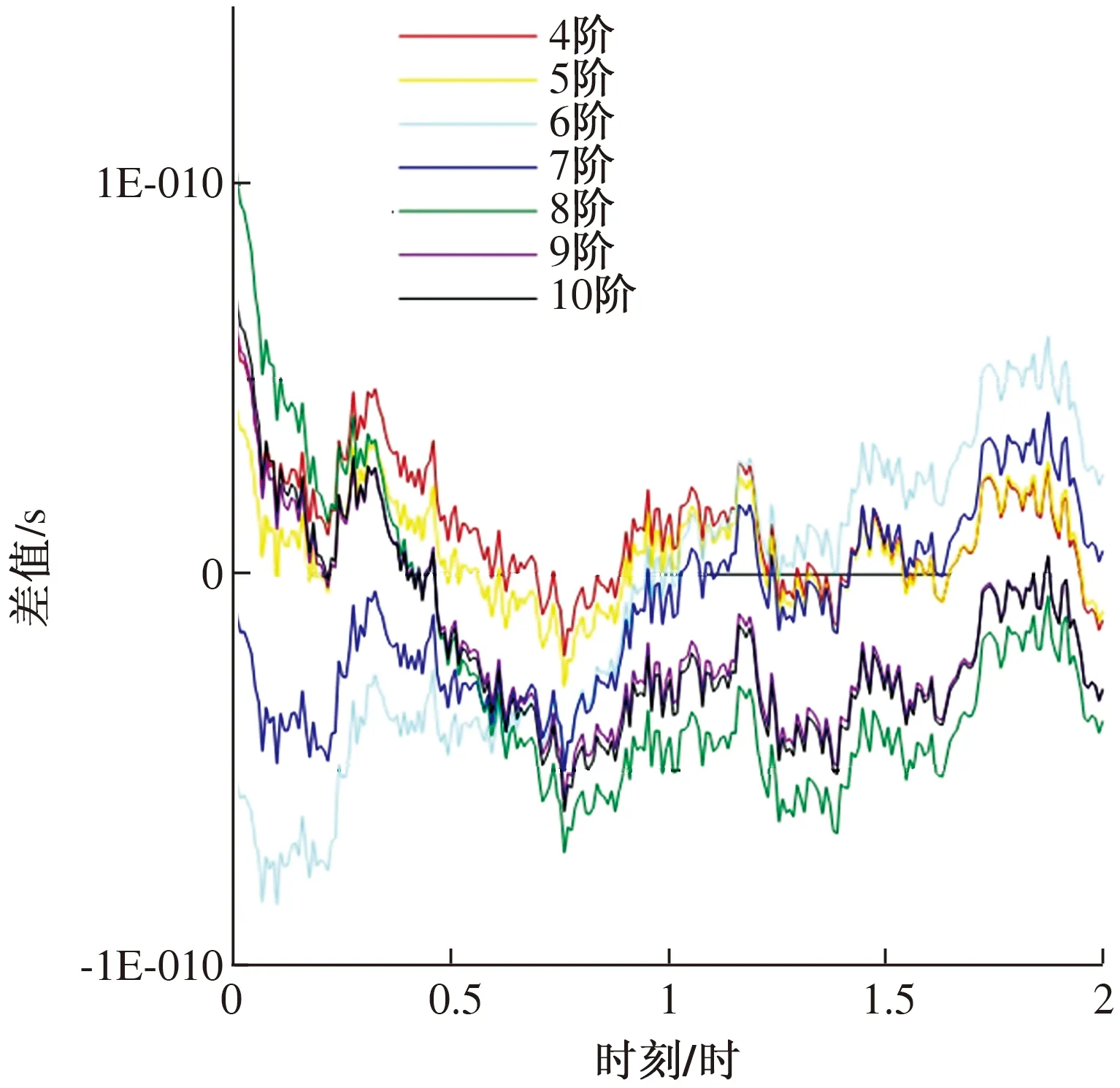
图1 4～10阶Chebyshev多项式内插5 min采样间隔钟差的结果数据和网站下载的30 s数据差值图

2 实验分析及结论

实验选取IGS公布的2012年1月1日0时至24时的PRN01卫星的5 min时间间隔的卫星钟钟差作为原始数据。利用4～11阶Chebyshev多项式内插计算得到间隔为30 s的卫星钟差数据。以IGS服务网站上下载的相应30 s间隔的卫星钟差数据作为参考值，对30 s间隔的卫星钟差数据的各个时间节点求差，评价每组内插结果数据的质量。

图1为4～10阶Chebyshev多项式内插PRN01卫星在当天0时到2时的5 min采样间隔的钟差产品，内插成30 s间隔的结果数据和网站下载的30 s间隔数据的差值图。可以看出，4～10阶Chebyshev多项式内插5 min采样间隔钟差的结果数据和网站下载的30 s数据差值很小，都在-1 ns至1 ns的区间内。

图2为4～10阶Chebyshev多项式内插PRN01卫星在当天全天的5 min采样间隔的钟差产品，内插成30 s间隔的结果数据和网站下载的30 s间隔数据的差值图。可以看出，在16时10阶Chebyshev多项式计算出的结果和网站下载结果相差越来越远。图3为11阶Chebyshev多项式内插PRN01卫星在当天全天的5 min采样间隔的钟差产品，内插成30 s间隔的结果数据和网站下载的30 s间隔数据的差值图。可以看出，11阶Chebyshev多项式不适合内插精密星历产品。

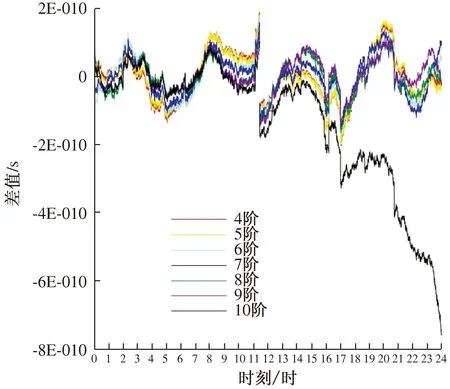
图2 4～10阶Chebyshev多项式内插5 min采样间隔钟差的结果数据和网站下载的30 s数据差值图

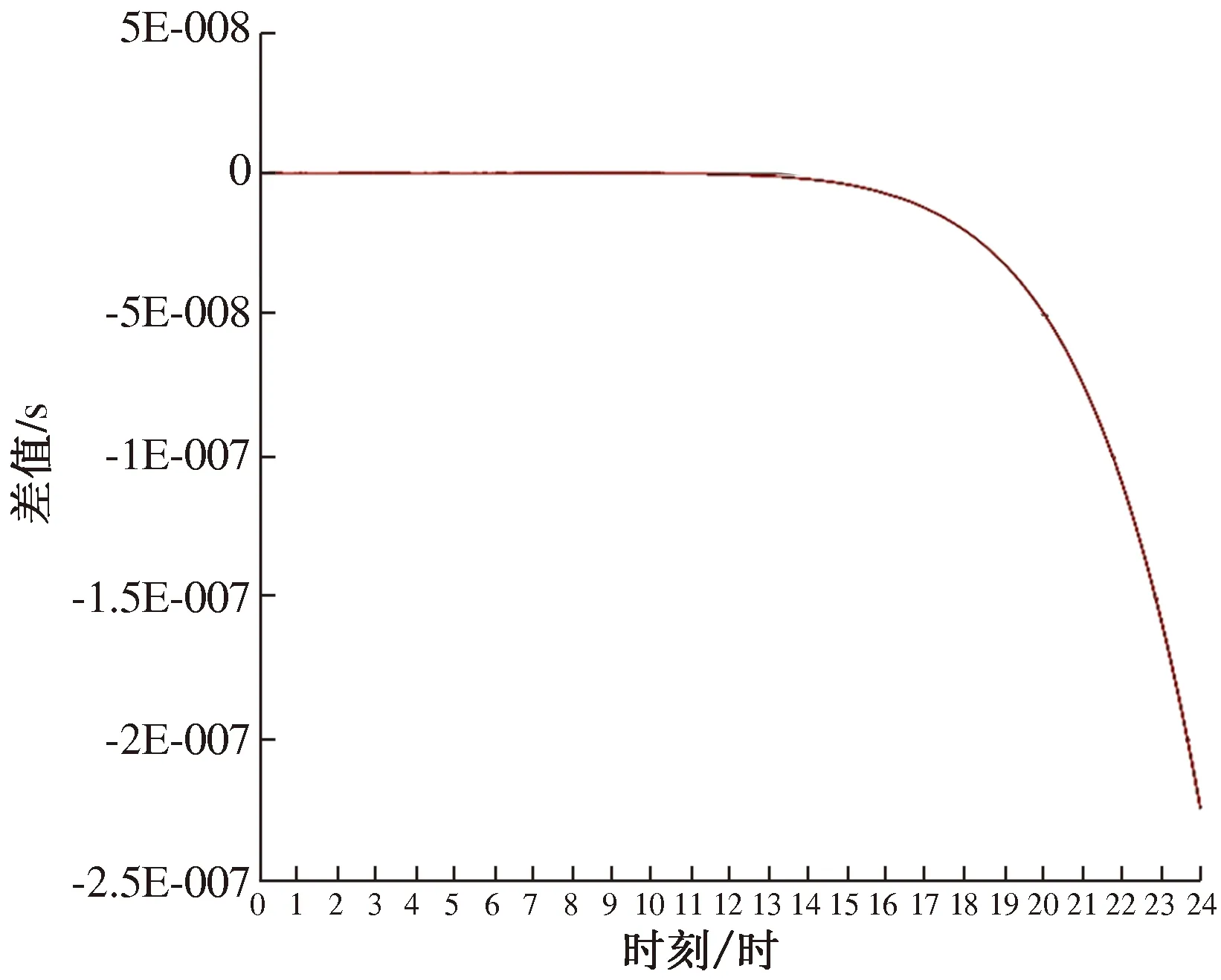
图3 11阶Chebyshev多项式内插5 min采样间隔钟差的结果数据和网站下载的30 s数据差值图

3～11阶Chebyshev多项式内插星历结果精度如表1所示。9阶Chebyshev多项式内插计算出的30 s钟差数据精度和准确度最高，最大值在亚纳秒级别，满足精密单点定位对卫星钟钟差的精度要求，在单个历元卫星钟钟差带来的距离误差控制在厘米级别。从4～10阶的平均值可以看出，用Chebyshev多项式内插采样间隔比较大的钟差数据从精度和质量的角度来看，完全可以满足要求。

表1 3～11阶Chebyshev多项式内插星历结果精度 ns

为了验证不同卫星钟钟差产品对精密单点定位的不同影响，方案一采用9阶Chebyshev多项式内插5 min间隔数据计算得到的30 s间隔数据，方案二采用IGS服务网直接下载的30 s间隔数据。

利用本文方法编写的PPP软件中观测值数据的预处理包括了剔除双频观测值不全、卫星高度角低于15度的数据和数据周跳探测和修复等工作。该软件实现了Hopfield 模型、Black 模型和Saastamoninen 模型。该软件包含了传统模型和Uofc模型。利用该软件进行了模拟试验，试验采用传统模型，参数估计策略为：测站参数采用参数估计和常数处理策略，接收机钟差采用参数估计和白噪声处理策略，对流层的天顶延迟采用参数估计和随机游走的策略，模糊度参数采用参数估计和常数处理，若发生周跳，则重置参数，重新估计。图4为该软件的主界面，图5为该软件的试验结果示意图。

图5 本文软件试验结果截图

两种方案的数据精度和收敛速度如图6、图7所示。两种方案的全天结果平均值比较如表2所示。

图6 方案一的结果精度

图7 方案二的结果精度

表2 方案一和方案二的全天结果平均值比较

试验结果显示，该软件定位精度不高。在定位的前期，定位结果偏差较大，随着时间的推移，定位误差就会徘徊在20 cm以内。这是因为试验选用了传统模型，组合模糊度破坏了单频载波模糊度的整数性质，固定起来比较复杂和费时，需要反复迭代才能达到伪固定，且精度不高，当数据量达到一定数量时，趋于稳定。但是总体看，单历元东、北以及天顶方向精度都在20 cm以内，结果数据的外符合精度达到预期的要求，而且两种方案在定位结果的收敛速度上和结果精度上都是相差不大的，在东、北和天顶方向相差都比较小。因此，Chebyshev多项式内插计算得到的钟差产品可以满足精密单点定位的需要。

[1]楼益栋. 导航卫星实时精密轨道与钟差确定[D].武汉：武汉大学，2008.

[2]晏新村.精密单点定位技术在海洋测量中的应用研究[D].郑州:解放军信息工程大学，2013.

[3]于合理,郝金明,宋超,等.卫星钟系统偏差对精密单点定位精度的影响[J].测绘科学技术学报，2013(2): 136-139.

[4]王宇谱,吕志平,宫晓春,等.几种卫星钟差预报模型预报效果的分析与比较[J].大地测量与地球动力学，2015(3): 373-378.

[5]李鹏. GPS精密单点定位若干关键问题研究[D].成都：西南交通大学，2008.

[6]崔希璋.最小二乘原理的进一步推广[J].测绘学报，1983, 12 (1) : 12-20.

[7]洪樱,欧吉坤,彭碧波.GPS卫星精密星历和钟差三种内插方法的比较[J].武汉大学学报(信息科学版),2006,31(6):516-518.

[8]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005.

[9]李明峰,江国焰,张凯.IGS精密星历内插与拟合法精度的比较[J].大地测量与地球动力学,2008,28(2):77-79.

[10]叶聪云,罗涛,陈远,等.精密卫星钟差的内插方法研究[J].测绘信息与工程,2008,33(1):11-13.

Analysis of Chebyshev polynomial fitting GPS satellite clock error product in precise point positioning

YANG Huai-yi1, YANG Xing-yao2, WANG Shuai2

(1.ShanxiTeamofChina’sBuildingMaterialsIndustryGeologicalProspectingCenter,Taiyuan030000,China; 2.NanyangUrban&RuralInstituteofPlanning&Mapping,Nanyang473000,China)

In precise point positioning, satellite ephemeris product, observations and satellite clock error product need to achieve synchronization of time. Using the chebyshev polynomial, we interpolate satellite clock error product, 4 to 10 order chebyshev polynomial interpolation results reach the level of nanoseconds, and when the order is 9, the precision is the highest. Then the interpolation results applied to the precise point positioning. Experiments show that the chebyshev polynomial interpolation to calculate the clock error product can completely meet the needs of precise point positioning.

precise point positioning；satellite clock error；Chebyshev polynomial

2015-07-16

广西空间信息与测绘重点实验室资助课题(桂科能130511407)

杨怀义(1988-)，男，陕西渭南人，助理工程师。

1674-7046(2015)05-0067-05

10.14140/j.cnki.hncjxb.2015.05.013

P22

A