基于粗集的面实体动态空间方向关系研究

冯弟飞，胡圣武

(1.中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081;2.河南理工大学 测绘与国土信息工程学院，河南 焦作 454000)



基于粗集的面实体动态空间方向关系研究

冯弟飞1，胡圣武2

(1.中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081;2.河南理工大学 测绘与国土信息工程学院，河南 焦作 454000)

为了研究不确定面实体与确定面实体之间的动态方向关系的性质，利用粗集理论和方向关系矩阵模型进行分析。分析结果表明：随着不确定面实体动态变化，其方向关系也是变化的。其结果更能表达客观的实际情况。因此，该成果可以完善方向关系研究的内容，具有一定的理论价值。

不确定性；粗集；动态方向关系；面实体

方向关系是拓扑关系的重要研究内容，也是地理信息系统学科中的一个重要的研究方向。在空间目标之间，方向关系是一种重要的和基本的关系，它在空间推理、空间查询和空间分析等过程中起着重要作用[1-3]。

目前空间方向关系研究是假设在空间实体是确定的，没有误差条件下进行的。由于地理实体的复杂性，不确定性成为地理实体的一种内在属性，是地理实体的一种本质特征。地理实体的不确定性是由很多因素引起的，很多学者对此进行了研究，如胡圣武、郭继发等。地理实体存在不确定性得到了认可，很多因素都可引起不确定性，如地理实体的数字化、管理以及变换等，具体可参阅文献[4-9]。面实体数据的存储处理也有可能出现偏差和不确定性[10-11]。因此，现有的方向关系模型不适用不确定性地理实体的方向关系研究。本文引入粗集理论，来研究面实体之间的方向关系。本文的研究仅局限于不确定的动态区域和确定区域之间的方向关系。

1 粗集理论

粗集理论是由Pawlak在1982年提出的，主要是研究不完整数据、不精确知识的表达、学习、归纳等的方法，直接从给定问题的描述集合出发，通过不可分辨关系和不可分辨类确定问题的近似域，找出问题内在规律[12-13]。

设U是一个有限元素论域，X是U上的元素集合，X⊂U，R是论域U上的元素等价关系，[x]R是R元素等价类，所有等价类集合记作IND(R)。

定义3 称BNR(X)是X⊂U的R边界，而且BNR(X)=R-(X)-R-(X)。Pos(X)=R-(X)称作X的R正域；NegR(X)=U-R-(X)称作X的R负域。

定义4 设X⊆U且X≠φ，则称αR(X)=card(R-(X))/card(R-(X))为X⊆U的近似精度，式中card(S)表示S的基数。αR(X)表示获得关于集合X的知识是否完全的程度。

2 不确定区域用粗集表示

粗集区域的变化有2种形式[3]：下近似集变化而导致粗集区域的变化；粗集近似精度αR(X)变化而引起粗集区域的变化，其公式为

(1)

有两种情况：(1)在近似精度αR(X)不变的情况下，当下近似集区域增大，即R-(X)增大、R-(X)也增大，当下近似集区域变小，R-(X)也变小。(2)在R-(X)不变的情况下，当αR(X)(范围是0到1)增大时，则R-(X)变小、上近似集区域也变小；当αR(X)变小时，上近似集区域变大。图1表示第一种情况的变化；图2表示第二种情况的变化。为方便研究，α取0.5、0.7、0.9，取0.5表示α减小，取0.9表示α增大，图1、图2所表达的结论是变化趋势更直观，并非某个取值(如0.5或0.9)所得到的结果。

图1 下近似集变化导致粗集区域的变化

图2 近似精度变化导致粗集区域的变化

3 动态方向关系

以确定区域A为参照物，不确定区域B为源目标，研究因α值的变化引起B的区域发生变化，从而引起方向关系的变化。针对A、B建立矩阵方向关系矩阵模型(见图3)，它们的方向关系为D={E,SE}。

3.1 当不确定区域B的α变大

(1)当下近似集变大，上近似集不变，精确度α值变大，α值变大说明目标对象B精度变大，由图3变为图4，A、B的方向关系仍为D={E,SE}，没有发生变化(见图4)。

图3 确定区域A和不确定区域B的方向关系模型

图4 近似精度α变大导致方向关系的变化

(2)下近似集与上近似集同时变大，但下近似集与上近似集的比值在增大，即近似精度α变大，因而目标区域B的区域变大，由图3变为图5，因此,它们的方向关系由D={E,SE}变为D={S,E,SE}。

(3)下近似集变小，上近似集变小，下近似集与上近似集同时变小，但下近似集与上近似集的比值在增大，即近似精度α变大，因而目标对象B区域变小，由图3变为图6，因此它们的方向关系由D={E,SE}变为D={SE}。方向关系矩阵如图6所示。

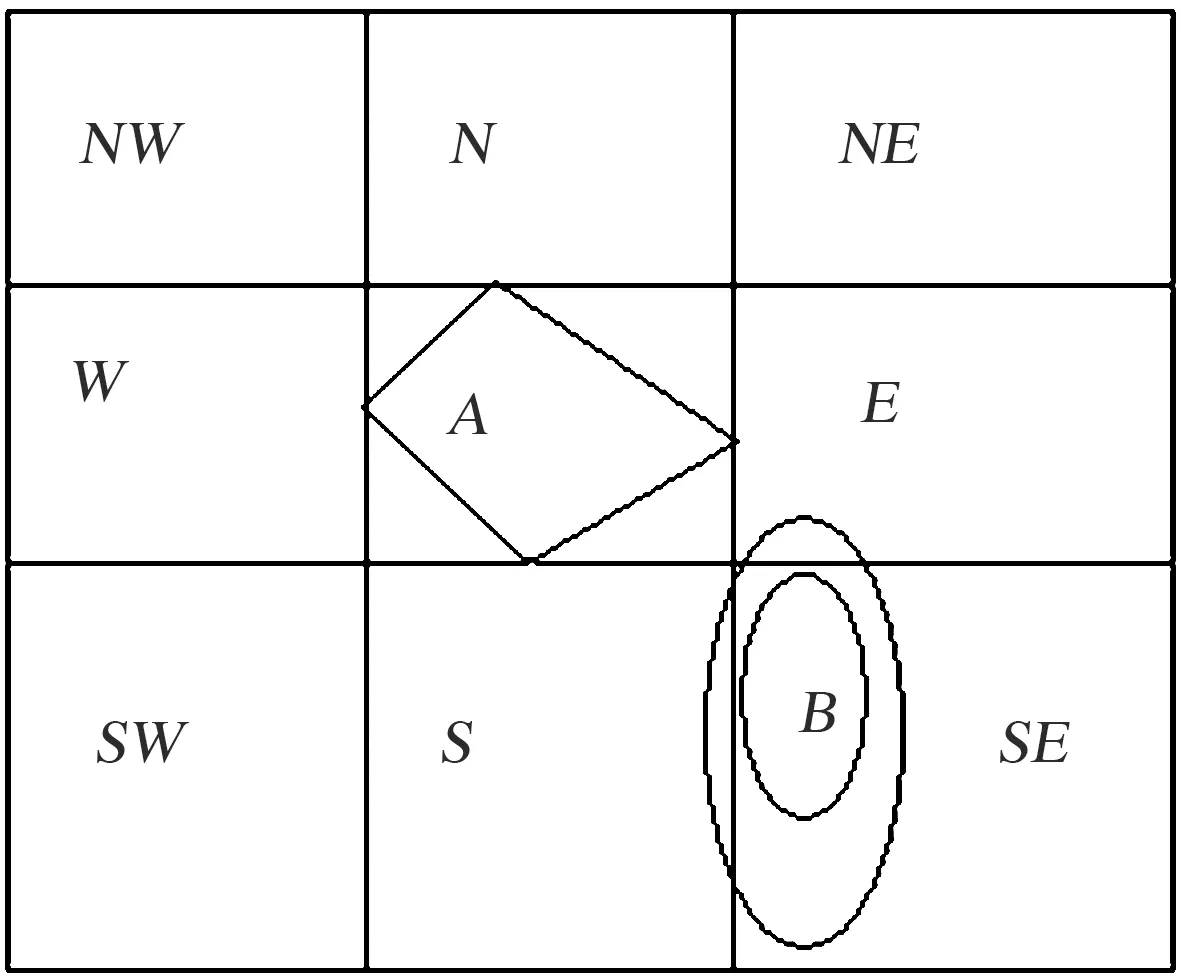
图5 不确定区域B变大导致方向关系的变化

图6 不确定区域B变小导致方向关系的变化

(4)下近似集不变，上近似集变小。这说明目标对象区域变小，精度提高，方向关系模型由图3变为图7。它们的方向关系由D={E,SE}变为D={SE}。

3.2 当不确定区域B的α变小

(1)当下近似集变小，上近似集不变时，精确度α值变小，不确定区域粗糙精度变低，方向关系模型由图3变为图8，A、B方向关系仍为D={E,SE}。

图7 B的上近似集变小和α变大导致方向关系的变化

图8 近似精度α变小导致方向关系的变化

(2)下近似集变小，上近似集变大，它们的相对精度变小，而不确定区域B的区域变大，方向关系模型由图3变为图9。在图9a中，它们的方向关系由D={E,SE}变为D={S,E,SE}；在图9b中，它们的方向关系由D={E,SE}变为D={O,S,E,SE}。

图9 不确定区域B变大和α变小导致方向关系的变化

(3)下近似集变小，上近似集变小, 它们的相对精度变小，但不确定区域B的区域变小，方向关系模型由图3变为图10，因此，它们的方向关系由D={E,SE}变为D={SE}。

(4)下近似集不变，上近似集变大,不确定区域B的区域变大，精度降低，方向关系模型由图3变为图11，它们的方向关系由D={E,SE}变为D={S,E,SE}。

图10 不确定区域B变小和α变小导致方向关系的变化

图11 B的上近似集变大和α变小导致方向关系的变化

4 结 语

本文研究了不确定区域与确定区域的动态方向关系，其结果更能体现客观实际的变化，因而是科学的。由于地理实体是变化的、不确定的，因此还需要进一步对方向关系进行研究。

[1]杜世宏，王桥，秦其明.空间关系模糊描述与组合推理[M].北京：科学出版社，2007.

[2]黄娟娟,周世健.粗糙集理论在GIS 数据处理中的研究与应用[J].江西测绘，2009，27(2)：2-4.

[3]胡圣武，谢歆.基于粗集的区域之间动态拓扑关系的研究[J].河南理工大学学报(自然科学版)，2015,34(3)：356-365.

[4]翟书礼,胡圣武.基于粗集的面实体之间拓扑关系[J]. 地理空间信息,2014,12(2):93-95.

[5]孙卫星,胡圣武.基于粗集的动态拓扑关系研究[J]. 地理空间信息,2015,13(3):25-28.

[6]关胜况,胡圣武.基于粗集的面实体方向关系的研究[J]. 地理空间信息,2015,13(2):98-101.

[7]胡圣武.GIS不确定性的基本理论及需解决的问题[J].测绘科学,2007,32(2):125-127.

[8]胡圣武,王新洲,潘正风,等.论GIS中的模糊不确定性以及处理方法[J].武汉大学学报(信息科学版),2005,30(5):12-16.

[9]谢振红,付博,王忠礼,等.地图数字化的不确定性分析及数据质量控制[J].吉林建筑工程学院学报,2010,27(6):6-9.

[10]胡圣武.GIS质量评价与可靠性分析[M].北京：测绘出版社，2006.

[11]郭继发,崔伟宏,刘臻,等.模糊地理实体不确定性综合描述研究[J].武汉大学学报(信息科学版),2010,35(1):46-50.

[12]裴海峰.Z.pawlak粗集推广与应用研究[D].济南：山东大学，2007.

[13]刘清. Rough集及Rough推理[M]. 北京：科学出版社，2001.

Dynamic spatial direction of spatial entities based on Rough set

FENG Di-fei1，HU Sheng-wu2

(1.GuiyangEngineeringCo.Ltd.,ChinaElectricPowerConstructionGroup,Guiyang550081,China; 2.SchoolofSurveying&LandingEngineering,HenanPolytechnicUniversity,Jiaozuo454000,China)

In order to study the nature of the relationship between the dynamic direction uncertain plane entity and determine surface entities, analysis was made by using rough set theory and direction relation matrix model. The results showed that with the dynamic changes of uncertain plane entity, the relationship is also changing its direction. The results are better able to express an objective reality. Thus, the results of research can improve the content of direction relations, which has some theoretical value.

uncertainty；Rough set；dynamic direction relationship；spatial entity

2015-06-28

国家自然科学基金委员会-河南省人才培养联合基金(U1304401)

冯弟飞(1976-)，男，贵州贵阳人，高级工程师。

1674-7046(2015)05-0050-04

10.14140/j.cnki.hncjxb.2015.05.010

P208

A