基于立体视觉技术的实时测距系统研究
2015-04-25韩峻峰
王 帅,韩峻峰
(1.桂林电子科技大学 电子工程与自动化学院,广西 桂林541004;2.钦州学院 物理与电子工程学院,广西 钦州541099)
测距系统在民用及军事方面有着广泛的应用,航天测距、汽车防撞、机器人视觉导航、军事勘测等都需要测距系统进行实时测距。现代测距方法主要有激光测距、超声波测距、雷达测距、立体视觉测距等,其中,激光、超声波、雷达测距由于是主动式测距,通过对其原理的分析可发现,这些测距方法较易实现实时测距。而立体视觉测距,则受制于图像匹配技术难点、计算量大、硬件水平等,较难实现实时测距。目前立体视觉技术的研究大都偏向于三维重建及各种静态测量的应用[1]。
但对于现代测距系统的发展方向趋向于智能化,为立体视觉测距提供了广阔的应用平台,作为被动测距,立体视觉技术无需向目标物发射任何信号,只需通过图像传感器采集到图像对,由于图像中包含的信息远大于以上传统测距方法,通过对图像信息的识别、监测,将能有效地提高测距系统的智能化。因此,研究基于立体视觉技术的实时测距系统具有一定的应用价值。
1 双目立体视觉原理
双目立体视觉通过平行放置的两台摄像机对同一目标物进行图像采集[2],由于所采集的两幅图像间会存在不同程度的像素差,即视差,再通过一定的方法将视差提取出来,结合三角测量原理,便可得到目标物相对于两摄像机的深度距离。为便于观察,采用简化的双目立体视觉测距原理如图1所示。
如图1所示,为双目立体平行俯视几何成像图[3],左右摄像机严格平行放置,OL和OR为左右两摄像机光心,IL、IR分别为左右摄像机的像平面,CL、CR为左右像平面上的主点位置,其到光心位置的直线距离即摄像机的焦距f(理论上左右摄像机采用同一焦距,但实际由于摄像机工艺问题,同型号的摄像机也不可能所有参数相同),PL、PR为空间点P映射到左右像平面的投影,T是两摄像机光心OL到OR之间的平移距离,即为两摄像机之间的相对距离,Z便是目标点P的深度信息,即目标物到立体摄像机之间的距离。由图可得ΔPPMPL相似于ΔPPNOL,ΔPPMPR相似于ΔPPNOR。

图1 双目立体平行俯视几何成像图
根据相似三角形原理可得
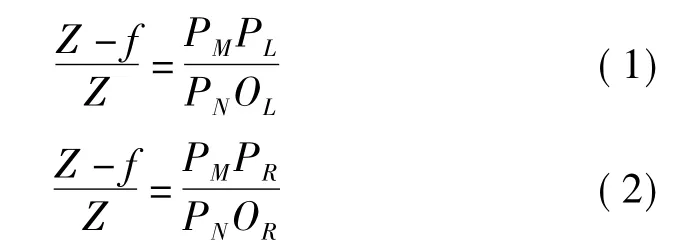
另PNOL=x,CLPL=l,PRCR=r,则代入式(1)和式(2)得

两式联立得出深度距离

其中,d=l-r,f已知,T已知。因此,若要求得Z值,只需获得空间点P在左右像平面投影点之间的视差值。
2 立体视觉实时测距系统实现
立体视觉实时测距系统的总体框图如图2所示,主要包括:图像采集、摄像机标定、双目立体校正、立体匹配、目标跟踪和数据输出等。
2.1 摄像机标定
摄像机标定方法有传统标定法和自标定法两种[4],传统标定法相较于自标定,算法较为复杂,不过精度较高。而自标定无需特定的参照物,仅通过运动过程中摄像机所采集周围环境的图像之间对应关系进行标定,相较于传统标定法,使用更灵活。

图2 立体视觉实时测距系统总体框图
由于系统使用固定的两摄像头进行图像采集,参数无过大变化,若采用自标定法,无异于增加运算消耗,且由于其使用未知参数过多,精度上难以与传统标定法相比美,不利于系统的实时性与精确性。因此,决定采用预标定法,即通过标定先得出摄像机的内部参数和外部参数,然后只需通过调用标定结果实现测距的目的,以减小系统的运算负担。
为建立三维世界坐标与二维图像坐标之间的对应关系,根据摄像机成像模型,可得空间点P在摄像机下的成像关系

其中,(Xw,Yw,Zw)是空间点p的世界坐标,(u,v)为空间点P投影在像平面点的坐标;Zc为空间点P在摄像机坐标系下光心到像平面投影点的距离;f/dx、f/dy分别为摄像机在横竖(x,y)方向的等效焦距,单位为像素;s为倾斜因子;u0,v0为图像坐标系下的主点坐标;R为3阶正交单位矩阵;t为平移向量,上式可简化为
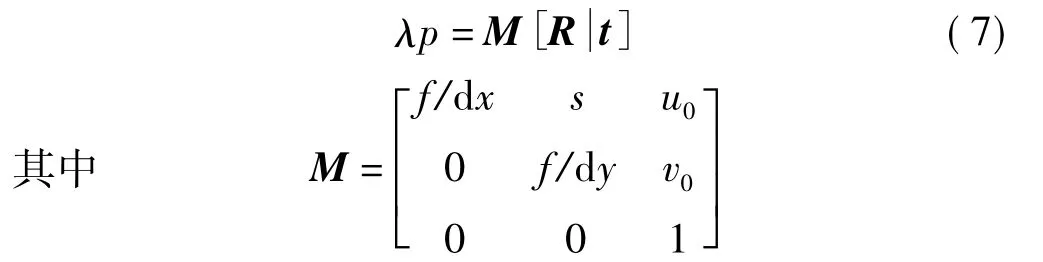
通过预标定法获取摄像机各参数,在此使用基于张氏标定法进行摄像机标定[5],但与张氏标定法不同的是同时考虑了摄像机的径向畸变和切向畸变,设计常用棋盘图作为摄像机的参照物,每个棋盘格大小为28 mm×28 mm,角点数为8×6,如图3所示。

图3 摄像机标定棋盘图
从不同角度拍摄标定板的多幅图像,这里使用OpenCV2.4.8(开源计算机视觉库)在VS2012编译环境下用C/C++编程进行图像捕获,图像采集模块使用两个天轮UVC-Scam摄像头,感光元件类型为CMOS,移动摄像机捕获左右各9幅不同角度的图像,图像大小为640×480,通过OpenCV内的cvStereoCalibrate()函数进行标定[6],标定结果如下

left_M、right_M给出了两摄像机内部参数,可看到,左摄像机和右摄像机焦距相同,主点分别近似为(333,249)和(332,253),left_D、right_D为左右摄像机的畸变系数矩阵。而摄像机外部参数,从旋转矩阵R可看出,R相似于单位矩阵,说明两摄像机基本处于平行状态,另外两摄像机实际设置距离为100 mm,这点从平移向量T的x向量为-100.671 98 mm可看出基本近似,误差较小,符合双目立体视觉测距系统的要求。
2.2 立体校正
由于摄像机工艺问题及光学透镜特性,一般镜头会有一些形变,即畸变。若不对此处理,将影响立体匹配的准确性,并使得立体匹配搜索图像对应点的范围扩大,产生较大的运算量,且耗时,不利于系统的实时性。而通过立体校正,可使得两幅图像严格的行对准,以便于匹配算法通过极限约束原则,将匹配对应点的二维搜索降为一维搜索,增加匹配的准确性与快速性[7]。
具体方法是通过给定的旋转矩阵R和平移向量T,利用Bouguet校正方法使左右图像中的每一幅重投影次数最小化,从而也使得重投影畸变最小化,同时使叠加视图的面积最大化。
由于三维点可通过投影矩阵变换到投影平面上的二维点。同理,平面上的二维点也可通过重投影矩阵重投影为三维点,即
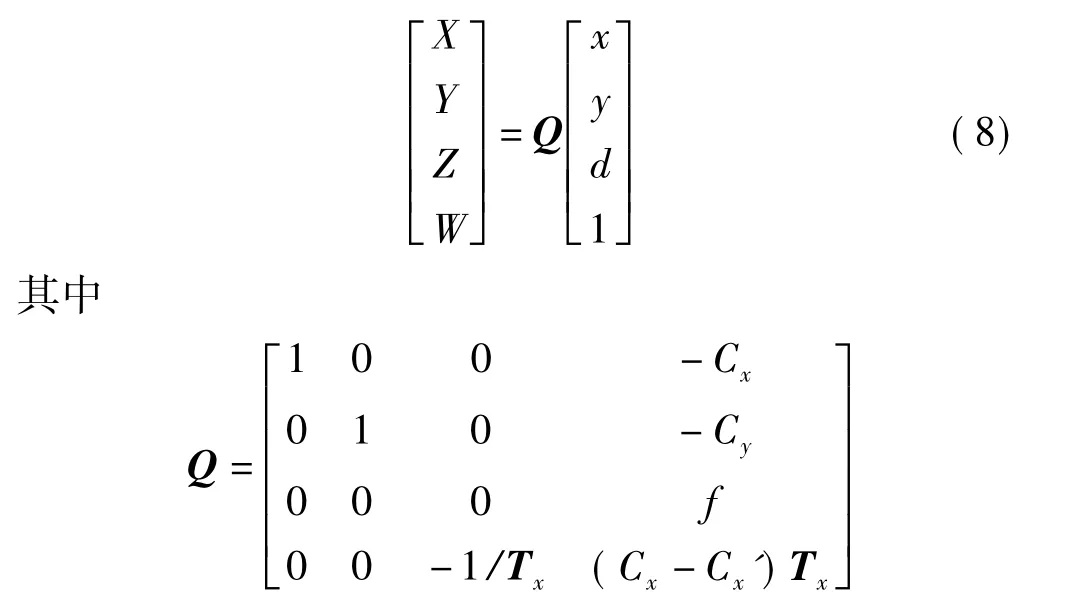
上式中,Q为重投影矩阵;d为二维齐次点的关联视差,重投影矩阵中,-Cx,-Cy和f均来自于图(a)的主点和焦距,Tx即图(b)摄像头相对左摄像头的平移距离;Cx'为主点在图(b)像上的x坐标,另外,若主光线在无穷远处相交,即Cx=Cx',则Q右下角的项为零。在OpenCV中可通过stereoRectify()函数实现以上校正功能,并获得重投影矩阵,校正结果如图4和图5所示。

图4 原图像校正前

图5 原图像校正后
2.3 立体匹配
立体匹配的目的是将两幅图像之间的匹配点建立相对应的关系,通过借助各种匹配代价函数并依托各种立体匹配算法实现图像的匹配过程。因此,立体匹配也是最消耗运算时间的部分,而选择一种合适的算法并对其进行参数优化则更为重要。
目前,立体匹配算法主要分为两类:基于局部约束的匹配算法和基于全局约束的匹配算法;而基于局部约束的匹配算法有特征匹配、相位匹配、区域匹配等算法[8-9]。通过对几种算法的简单实验验证及比对分析,在此采用区域匹配算法里的基于立体相关块匹配的方法,使用匹配代价函数为绝对误差累计(Sum of Absolute Difference)即SAD的方式来寻找两幅立体校正之后的图像之间的匹配点,SAD匹配代价函数如下

其中,原图中的像素块为IL,目标图中的像素块为IR,要搜寻的深度为d,所选匹配窗口大小为W,具体实现方法通过OpenCV中的cvFindStereoCorrespondenceBM()函数来完成,通过对该函数各个参数的调节,能较好地实现对两幅图像对应点的搜寻与匹配。图6所示为立体匹配后得出的视差图,图7为原图。

图6 视差图

图7 原图
通过视差图可直观地看到,若匹配点稠密,则视差图与原图的相似度就越高。
2.4 动态视差搜寻
对于立体匹配,根据摄像机成像原理,不难发现,目标物的视差与距离成反比。因此,若采用固定的搜寻深度,将造成远距离不必要的运算浪费或者近距离无法找到匹配点的问题。针对这一问题,现通过采用动态的视差搜寻范围来解决。
具体实现方法根据深度距离计算公式,又由于匹配算法要求搜寻深度范围为16的整数倍,因此可得公式

而两摄像机主光线通常会在有限距离内相交,即Cx≠Cx',因此深度距离公式修改为

则式(10)修改为

视差搜寻深度与距离成反比,n的取值总是向上取整。
2.5 目标追踪
目标追踪通过CamShift(Continuously Apative Mean-Shift)算法来实现[10],该算法将目标的其他色彩空间转换到HSI空间,并用其中的H(色调)分量做1D直方图计算,然后根据此特征,对视频图像中的每一帧进行Mean-shift运算,并将上一帧的处理结果作为下一帧Mean-shift算法追踪窗口(Search Window)的初始值,以此迭代下去。
图8 目标追踪效果图

图9 目标颜色直方图
3 实验结果及分析
基于块匹配的BM算法速度快,加入目标追踪算法后,经实验验证,在每秒25帧的情况下,测距速度达到ms级,能有效的进行目标追踪及获取目标视差图,并无明显卡顿现象。
为实现目标的实时追踪与测量,在通过CamShift算法取得目标所在收敛窗口时,根据此收敛窗口,同时在视差图相同区域遍历所有视差,依据最大视差原则选择目标视差,采用式(11)计算目标距离,并将距离实时显示在目标图上。
实验环境下,实时目标追踪与测量效果如图10所示。

图10 实时目标追踪与测量效果图
由图12可看出,对于所选物体,其下方实时显示数字即为其到摄像机的相对距离,单位为mm。为便于分析立体视觉距离测量精度,特移动目标来改变目标物与摄像机的相对距离,以测得目标在不同距离下的深度数据,具体实验结果如表1所示。

表1 实验结果
通过实验结果可看出,近距离测量精度较高,随着距离的增加,在一定范围内,系统测量与实际测量误差≤5%,说明此算法能达到一定的精度,但也可看出,较远距离误差增加明显,这主要是因标定产生的误差及实际测量产生的误差及其他因素的影响,如像素对物体不同距离的收纳以及匹配算法对强纹理的需求都会导致远距测量精度的下降。
4 结束语
通过对双目立体视觉的各关键技术进行研究之后,采用基于张氏标定法进行摄像机标定,并在此基础上考虑摄像机切向畸变对图像的影响,通过对图像的立体校正之后,使得立体匹配可根据极限约束法则进行匹配点匹配,大幅减少了运算量。而相比匹配算法的传统静态视差范围搜索方法的局限性,特采用动态视差范围搜索方法,优化了匹配参数,解决了不同距离匹配过程中运算浪费和找不到匹配点问题,并结合目标跟踪算法,实现了对目标的实时跟踪与测量。经实验验证,该系统成本低、可行性高,测距速度达到ms级,能实时对目标进行监测,并在一定范围内有较高的精度,具有一定的应用价值。
[1] 刘砚秋.机器视觉技术的发展动态[J].电子元件与材料,2014,33(5):93-94.
[2] 刘盼,王金海.基于平行双目立体视觉的测距系统[J].计算机应用,2012,32(S2):162-164.
[3] 王浩,许志闻,谢坤,等.基于OpenCV的双目测距系统[J].吉林大学学报:信息科学版,2014,32(2):188-194.
[4] 刘金颂,原思聪,张庆阳,等.双目立体视觉中的摄像机标定技术研究[J].计算机工程与应用,2008,44(6):237-239.
[5] 岳晓峰,祁欢.基于张正友平面模板法的双目立体视觉系统标定[J].机械工程师,2014(2):1-3.
[6]Gary Bradski,Adrian Kaehler.Learning openCV[M].Beijing:Tsinghua University,2009.
[7] 刘怡光,孙柏林,石勇涛,等.用于3维重建的立体图像校正[J].四川大学学报:工程科学版,2013,45(3):79-84.
[8] 白明,庄严,王伟.双目立体匹配算法的研究与进展[J].控制与决策,2008,23(7):721-729.
[9] 于乃功,马春燕,林佳.基于双目视觉的关键点的检测方法及定位研究[J].计算机测量与控制,2011,19(7):1565-1568.
[10]杨杰,穆平安,戴曙光.一种改进Camshift算法的研究[J].计算机应用与软件,2014,31(2):167-170.
