微电网优化调度仿真模型
2015-04-25马金祥朱锡芳范新南罗成名袁洪春
马金祥, 朱锡芳, 范新南, 罗成名, 袁洪春
MA Jin-xiang1,2, ZHU Xi-fang1, FAN Xin-nan2, LUO Cheng-ming2, YUAN Hong-chun1
(1.常州工学院 电气与光电工程学院,常州 213002;2.河海大学 江苏省输配电装备技术重点实验室,常州 213022)
0 引言
微电网是一种新型的电力系统网络结构,是实现主动配电网的有效方式。开发和延伸微电网能够促进分布式发电与可再生能源的大规模介入,促进传统电网向智能电网过渡[1]。同时,微电网是一个可以实现自我控制、保护和管理的自治系统,它作为完整的电力系统,依靠自身的控制及管理功能实现功率平衡控制、系统运行优化、故障检测与保护、电能质量治理等方面的功能[2]。发展微电网是解决分布式发电并网和偏远地区或海岛供电的有效途径,具有十分广阔的应用前景[3]。微电网作为集成多种分布式电源、储能装置和用电负荷于一体的可控系统,具有双向能量流和信息流的复杂特性。
微电网优化调度是一个多目标、多约束、多时段、非线性的组态复杂控制问题。微电网既可以与大电网并网运行,也可以脱离大电网孤立运行。微电网通过公共耦合点与大电网相连,实现并网运行,需对微电网进行建模以研究微电网接入。文献[4]从微电网基本元件出发,基于微电网物理背景,借鉴负荷建模理论,提出了微电网整体建模的思路,将风力发电机、电动机等动态元件等效为等效电机模型,并从理论上推导了等效电机的通用模型。文献[5]针对微电网分布式电源详细模型的本质特点,对其组成部分原动机和逆变器分别进行简化,提出相应的简化模型。文献[6]以独立的系统仿真模块和运行优化模块为核心,建立了微电网多目标动态优化调度的一般模型。文献[7]针对微网中风能和太阳能等可再生能源具有随机性和波动性的特点,提出了一种考虑随机性的微网能量优化调度模型。文献[8]考虑微电网的不对称性和逆变电源控制特性的多样性,提出适用于微电网三相潮流计算分析的数学模型。微电网的调度模型直接影响着微电网运行方案的可行性和合理性,是微电网优化调度研究的核心内容。
元胞自动机(Cellular Automata, CA)是由波兰数学家Stanislaw Marcin Ulam于20世纪40年代提出,由John Von Neumann用于自复制逻辑系统性研究的一种在时间、空间和状态上都离散的动力系统建模方法,具有模拟复杂动态系统时空演进的能力。文献[9]提出一种采用元胞自动机模拟城市土地利用的逐年发展过程进而进行城市配电网空间负荷预测方法。文献[10]采用元胞自动机模拟城市土地利用动态发展过程,预测规划区域各小区土地的未来使用类型。文献[11]基于Fisher判别方法和元胞自动机模型提出了一种微电网格局计算方法,该方法较少考虑微电网总体供需平衡。
元胞自动机理论“自下而上”的研究思路,综合系统整体供需平衡理论,较全面的考虑了微电网局部与整体的协调一致,使得微电网调度模型更适合模拟实际运行情况。微电网优化调度对提高微电网用户自律性和需求侧管理具有重要意义,也是实现用户和电网利益最大化的基础。
1 元胞自动机模型
元胞自动机是指在空间上规则排列的一系列元胞组成的网络。标准元胞自动机是一个四元组[12]:A=(Ld,S,N,f)。其中:A为自动元胞机系统;Ld表示d维元胞空间,d为元胞空间的维数;S表示元胞自动机的状态集合;N表示一个所有邻域内元胞的集合(包括中心元胞);f表示中心元胞域邻居间的状态转换规则。这里主要研究John Horton Conway的“生命游戏”(Game of Life)元胞自动机模型。“生命游戏”模型为二维(d=2)元胞自动机模型,并选择Moore型邻居模型。
“生命游戏”模型每个元胞都可以看成是一个生命体,都有“生”或“死”两种状态,0代表“死”,1代表“生”。每个元胞周围均有8个邻居。元胞与其邻居构成的3×3的网格称为元胞空间基本单位。元胞的下一迭代步长的状态,只与其构成的基本单位状态有关。
元胞自动机转换规则是元胞自动机的核心,根据元胞当前状态及其邻居状态确定下一时刻该元胞状态的动力学函数。简单而言,元胞自动机转换规则就是元胞状态转移函数,状态转移函数可记为:

其中,sxy(t)和sxy(t+1)分别为点(x,y)在t时刻和t+1时刻的状态,而在t时刻的邻居数量。其中,
“生命游戏”元胞自动机模型状态转移函数[13]:

二维元胞自动机的通用状态转移函数表示为:

为了进一步描述“生命游戏”的特征,这里定义了一些相关函数:

sum (t )和ρ ( t)表示元胞空间中生命数量和密度,两者之间存在比例关系;avg(t)表示生命数量统计平均值,描述生命数量总体变化趋势;d(t)表示状态“1”与状态“0”之间的距离均值;MSE(t)为均方差,描述生命点之间的离散程度。其中,L×L为整个元胞空间,表示生命点均值坐标。
“生命游戏”元胞自动机运行模式主要可分为静止、振荡器和飞船三种。PD模式是周期为15的振荡器,是由康威在1970年跟踪行元胞运行轨迹时发现的。实际上,将10个元胞排成一行,也能够演化为PD模式。PD模式是非常著名的周期超过3的“生命游戏”元胞自动机振荡器。
PD模式B3/S23规则的sum(t)和avg(t)如图1所示,PD模式B3/S23规则的d(t)和MSE(t)如图2所示(仿真实验数据长度为40)。从图1和图2中可以看出,PD模式B3/S23规则呈现周期性的变化,周期为15。生命数量统计平均值avg(t)逐渐趋于稳定。PD模式B3/S23规则是一种稳定的运行模式。

图1 PD模式B3/S23规则的sum(t)和avg(t)

图2 PD模式B3/S23规则的d(t)和MSE(t)
2 元胞自动机变异规则与密度需求管理
“B3/S23规则”是基本的“生命游戏”元胞自动机规则,通过改变“生命游戏”规则,会引起出生规则、存活规则和死亡规则之间的平衡关系变化,并最终导致生命数量的动态变化。如加强出生规则因素、加强存活规则因素和(或)削弱死亡规则因素,则生命数量会趋于增加;反之,如削弱出生规则因素、削弱存活规则因素、和(或)加强死亡规则因素,则生命数量会趋于减少。
密度一般定义为某种物质质量与体积的比值,这里指一定元胞空间中生命的数量与整个元胞空间可容纳生命数量之间的比值。元胞自动机密度需求管理的任务是根据需要的生命数量,调整元胞自动机状态转移函数(迭代规则),使元胞生命数量增加或减少,并最终实现系统对元胞生命数量的需求目标。迭代规则的调整在“B3/S23规则”的基础上进行。
“B3/S123规则”是“B3/S23规则”的变异规则之一。“B3/S123规则”在“B3/S23规则”的基础上增加了存活规则“S1”,则意味着有更多的元胞会在下一迭代步长中继续存活。在同等情况下,元胞在“B3/S123规则”中比在“B3/S23规则”中有更多的存活可能性。初始条件10×1模式B3/S123规则仿真实验结果如图3和图4所示。

图3 10×1模式B3/S123规则的sum(t)和avg(t)

图4 10×1模式B3/S123规则的d(t)和MSE(t)
从图3中可以看出,尽管生命数量sum(t)出现了波动情况,但其总体趋势是增加的,因为avg(t)呈现稳步增加。另外,从图4中可以看出,随着生命数量增加,生命数量之间的离散程度也逐渐增加。
“B3/S3规则”也是“B3/S23规则”的变异规则。“B3/S3规则”在“B3/S23规则”的基础上减少了存活规则“S2”,则意味着更少的元胞会在下一迭代步长中继续存活。在同等情况下,“B3/S3规则”比“B3/S23规则”元胞存活可能性明显减少。初始条件20×1模式、28×1模式实验结果如图5和图6所示。

图5 20×1模式B3/S3规则实验结果

图6 28×1模式B3/S3规则实验结果
从图5和图6中可以看出,尽管元胞数量sum(t)短时间出现了波动情况,但其总体趋势是减少的,直至最终减少至零。在图5中,avg(t)开始稳步减少在t=7,而sum(t)迭代为零在t=10。在图6中,avg(t)开始稳步减少在t=7,而sum(t)迭代为零在t=14。n×1模式B3/S3规则sum(t)和avg(t)实验结果如表1所示。
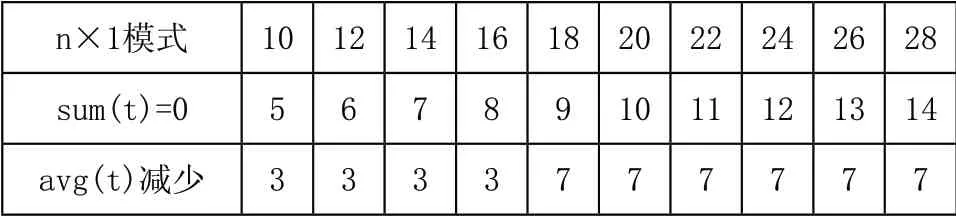
表1 n×1模式B3/S3规则sum(t)和avg(t)实验结果
3 仿真实验与结果分析
根据上述分析,本文选择30×30栅格的元胞空间进行仿真实验,模拟微电网孤岛运行模式。每个元胞空间均有两种状态,分为“供电状态”和“用电状态”。有生命的元胞表示“供电单元”,而无生命的元胞则表示“用电单元”。为简化问题,设每个“供电单元”的供电贡献为单位“1”;而“用电单元”的用电需求应小于单位“1”,通过总体用电需求量表示。“供电单元”的总体供电量应随“用电单元”总体需求量而变化,两者之间应保持平衡关系。
微电网总体供电量与用电需求期望值(exp)之间可以存在一定的允许误差,允许误差用AE表示,允许误差可分为三级:2%,5%和10%。
总体供电量t时刻的密度用 ( )tρ 表示,用电需求密度期望值用expρ 表示。其中,
如果在“B3/S123规则”或在“B3/S3规则”下供电单元迭代数量不发生变化,则进入“B3/S23规则”进行供电单元布局调节;
供电单元仿真模型初始条件可以为任意情况,为分析问题的方便,这里取初始条件为n×1,其中
初始条件10×1,期望值exp=100,允许误差AE=5%。供电单元密度需求管理仿真模型实验结果如图7和图8所示。实验结果:当t=25时,迭代结束。sum(25)=96,MSE(25)=13.181。
定义:time(n,exp,AE),sum(n,exp,AE),MSE(n,exp,AE)分别表示在初始条件n×1,期望值e x p,允许误差A E 条件下对应的供电单元密度需求管理稳定迭代时间(步长),统计值和均方差。可得,time(10,100,5%),sum(10,100,5%)=96,MSE(10,100,5%)=13.181。
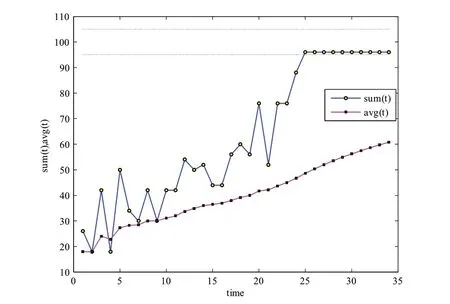
图7 10×1模式密度需求管理实验结果sum(t)和avg(t)

图8 10×1模式密度需求管理实验结果d(t)和MSE(t)
在期望值exp=100时,对于不同的初始条件n×1和不同的允许误差AE,time(n,100,AE),sum(n,100,AE)仿真实验结果如图9和图10所示。分别为期望值的下限和上限。
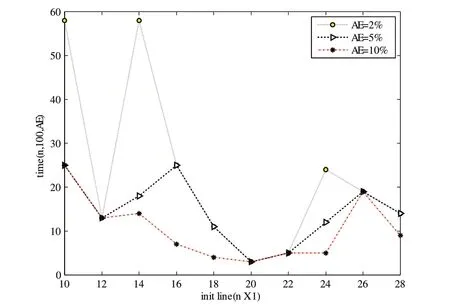
图9 time(n,100,AE)实验结果对比

故障原因定位准确、机理清楚,针对设计缺陷,采取的改进措施有效、可行。后续生产的DIM模块需重新制作PCB,减小耦合系数。遵循布局合理、数模隔离、扩大线间距、少走平行线、减少线长和不走环形线等设计原则。
通过以上的工作,彻底解决了某型飞机下显显示串扰的批次性质量问题,保证了飞机的批产和转厂工作的正常进行。
[1] 白剑林,张平定,体卫群,刘鹏.对第四代战斗机综合航电系统的构想[J].火力与指挥控制,2006,31(5):1-3.
[2] 刘杲靓.综合航空电子系统效能评估研究[D].西安:西北工业大学,2007.
[3] 张建东,高晓光,吴勇,等.综合航电显控仿真系统的设计与实现[J].火力与指挥控制,2006,31(2):40-43.
[4] 吴昊,陈少昌,王杰玉.高速数字系统的串扰问题分析[J].现代电子技术,2009,32(1):170-173.
