基于特征模型的火箭发动机伺服控制系统设计①
2015-04-25王元芝
樊 垚,李 亮,祁 鹏,任 章,王元芝
(1.北京航空航天大学 飞行器控制一体化技术国防科技重点实验室,北京 100191;2.上海机电工程研究所,上海 201109;3.第二炮兵驻航天科技集团第四研究院军事代表室,西安 710025;4.中国人民解放军96630部队,北京 102200)
基于特征模型的火箭发动机伺服控制系统设计①
樊 垚1,李 亮2,祁 鹏3,任 章1,王元芝4
(1.北京航空航天大学 飞行器控制一体化技术国防科技重点实验室,北京 100191;2.上海机电工程研究所,上海 201109;3.第二炮兵驻航天科技集团第四研究院军事代表室,西安 710025;4.中国人民解放军96630部队,北京 102200)
以新型大推力火箭发动机为研究对象,提出了基于特征模型的伺服系统控制器设计方法。首先,介绍了特征建模理论并讨论了特征模型参数范围;其次,采用人工蜂群算法实时估计火箭发动机伺服系统特征模型参数,使其满足特征模型输出与实际系统输出特性等价条件;最后,使用黄金分割自适应控制律保证系统在参数估计过程中的闭环稳定性,同时引入前馈跟踪控制律,逻辑积分控制律和逻辑微分控制律使伺服控制系统快速、精确跟踪线位移指令并改善动态性能。仿真结果表明,设计的火箭发动机伺服控制系统指令跟踪精度高,动态特性良好,鲁棒性强。
火箭发动机;伺服系统;特征模型;人工蜂群算法;黄金分割自适应控制律
0 引言
为满足日益增长的空天运输需求,新一代火箭必须使用大推力发动机以提高其运载能力,其伺服系统的负载特性对火箭控制性能有着决定性的影响。国内外众多学者应用先进控制理论,在液压伺服系统控制问题上取得了大量成果[1-4]。本文研究的新型大推力火箭发动机负载谐振特性与传统火箭发动机存在较大差别。文献[5]对该类发动机伺服系统动态特性进行了分析,使用直接数值寻优方法开展控制律设计。文献[6]针对液压伺服系统单谐振点问题,研究了陷波滤波器设计方法并给出了参数选择依据。经典设计方法要求在已知发动机谐振特性的基础上,开展控制系统设计,但发动机工作状态及工作环境都会影响谐振负载特性,通过冷、热试车实验只能得到其谐振特性的近似值。当谐振特性发生变化时,经典发动机伺服系统控制性能下降,甚至不满足指标要求。因此,可将火箭发动机伺服控制系统设计问题归结为一类不确定系统的控制问题。
吴宏鑫院士及其研究团队在长期从事不确定高阶线性系统控制问题研究的基础上提出基于特征模型的智能控制方法,该方法以全系数自适应控制理论为基础,利用低阶控制器控制高阶对象,易于工程实现,同时保证闭环系统具有强鲁棒性和干扰抑制能力[7-9]。本文采用该方法与人工蜂群算法相结合,研究火箭发动机伺服控制系统的设计问题。
1 火箭发动机伺服系统数学模型
本文以新型大推力火箭发动机伺服系统为研究对象,其主要动力学特性为发动机对伺服机构线位移输出产生的谐振作用,称之为负载效应。火箭发动机由喷管主质量M和管路系统附加质量m两部分组成,两部分之间存在弹性连接,引入双质量-弹簧-阻尼物理模型对发动机伺服系统进行数学建模分析,如图1所示。图1中,KM为伺服机构与主质量间的刚度系数;Km为主质量与附加质量间的刚度系数;Kh为液压弹簧效应系数;BM为主质量阻尼比;Bm为附加质量阻尼比;X1为伺服阀控制输入端线位移;X2为伺服机构线位移;X3为发动机喷管角位移,即主质量M位移;X4为附加质量m位移。

图1 发动机双质量-弹簧-阻尼物理模型Fig.1 Geminate mass-spring-damping model of the engine
发动机伺服系统负载效应为从控制输入端线位移X1到伺服机构线位移X2间的动态特性,在力平衡条件下求解传递函数,如式(1)所示,发动机伺服系统呈现双谐振点频率特性。
(1)

发动机质量分布复杂,式(1)所示伺服系统传递函数中各系数很难通过理论方法定量计算,该式只能定性解释双谐振点负载效应的产生机理。工程中,需要通过实验手段测定伺服系统的谐振频率特性,再根据频域辨识理论求解传递函数中的参数值。由于发动机伺服系统的谐振特性与其工作状态及外部环境有着密切的关系,通过冷、热试车实验测定的谐振特性与实际工作状态时的谐振特性会存在一定的差别。因此,发动机伺服控制系统必须适应谐振特性参数的不确定性,同时抑制高阶未建模动态影响,进而保证飞行控制系统的有效性。
2 火箭发动机伺服控制系统设计
2.1 火箭发动机伺服系统特征建模
特征模型理论为复杂高阶系统进行低阶控制器设计提供了理论依据,文献[7]证明如果控制器与特征模型组成的闭环系统稳定,就能保证控制器与原控制对象组成的闭环系统稳定。特征建模方法利用低阶时变差分方程可与高阶定常差分方程等价的基本原理,建立反映控制对象动力学的特征模型,根据其动力学特征和性能要求,把高阶系统的动力学特性信息压缩到几个特征参量之中[7-8]。线性定常系统的一般形式见式(2)。
(2)
定理1:对于线性定常对象G(s),在满足特定采样周期Δt的条件下,当要求实现系统位置保持控制或位置跟踪控制时,其特征模型可用一个二阶时变差分方程来描述,见式(3):
y(k+1)=α1(k)y(k)+α2(k)y(k-1)+
β0(k)u(k)+β1(k)u(k-1)
(3)
当对象G(s)稳定或含积分环节时,则有
(1)系数αi(k),βi(k)是慢时变的;
(2)系数的变化范围可确定;
(3)在动态过程中,特征模型的输出与实际对象输出误差可控,且在允许范围内;
(4)在稳态情况下,特征模型的输出与实际对象输出相等。
工程上,当控制对象为最小相位系统或弱非最小相位系统时,其特征模型可简化为式(4):
y(k+1)=α1(k)y(k)+α2(k)y(k-1)+β0(k)u(k)
(4)
文献[10]论述并证明了线性定常系统参数的范围,由于伺服控制系统使用二阶线性时变系统作为特征模型,所以这里仅讨论式(5)所示的二阶线性系统参数范围。
(5)
对式(5)进行离散化,并在系统输出端使用零阶保持器,则被控对象的离散差分方程如式(6)所示。这里,Δt为采样周期。
A(z)=(1-ep1Δtz-1)(1-ep2Δtz-1)
(6)
二阶线性系统(4)的参数α1、α2可表示为式(8)、式(9):
α1=ep1Δt+ep2Δt
(8)
α2=-e(p1+p2)Δt
(9)
定义Tmin为最小等效时间常数,Tmax为最大等效时间常数,则
e-Δt/Tmin≤epiΔt≤e-Δt/Tmax
(10)
将式(10)代入式(8)、式(9),可得α1、α2变化范围,如式(11)、式(12)所示。
2e-Δt/Tmin≤α1≤2e-Δt/Tmax
(11)
-e-2Δt/Tmax≤α2≤-e-2Δt/Tmin
(12)
由于0≤Δt/Tmax≤Δt/Tmin≤ηmax,可得差分方程各系数满足式(13)、式(14)。
2e-ηmax<α1<2
(13)
-1<α1<-e-2ηmax
(14)
定义p1Δt=-Δt/T1,p2Δt=-Δt/T2,当Δt/T1=0且Δt/T2=0时,α1+α2取极大值,当Δt/T1=ηmax且Δt/T2=ηmax时,α1+α2取极小值,取值范围见式(15):
2e-ηmax-e-2ηmax<α1+α2<1
(15)
为了满足控制器鲁棒性和参数估计精度,要求系统参数β0不能太小,文献[10]在理论证明的基础上进行合理假设,给出系统参数β0如式(16)所示:
(16)
式中D为静态增益;T′为等效时间常数。
取ηmax=1/3,Δt/T′∈(1/10,1/3),D∈(0.3,3)时,差分方程(4)系数属于有界闭凸集Ds,如式(17)所示:
(17)
2.2 基于人工蜂群算法的特征模型参数估计
文献[11]提出人工蜂群智能优化算法,该算法通过模拟蜜蜂采蜜行为解决参数优化估计问题[12],本文将其应用于火箭发动机伺服系统特征建模。人工蜂群算法将蜂群中的蜜蜂分为3类,分别为。工蜂、待工蜂和侦察蜂。食物源代表参数估计问题的可行解,食物源的适应度值代表了可行解的质量。人工蜂群算法流程图如图2所示[13-14]。

图2 人工蜂群算法流程图Fig.2 Flow chart of artificial bee colony algorithm
随机生成食物源种群(Xb1,Xb2,…,XbNe),这里,Ne是食物源的数量。食物源Xbi可表示为(xbi1,xbi2,…,xb,iD)代表可行解空间中第i个可行解。利用式(4)描述的火箭发动机伺服系统特征模型存在3个估计参数,j时刻的参数估计值即为人工蜂群算法中食物源,如式(18)所示:
θ(i,j)=Xbi=[α1(i,j)α2(i,j)β0(i,j)]T
(18)
通过式(19)初始化食物源位置:
xbij=xb min j+αij(xb max j-xb min j)
(19)
式中αij是[0,1]之间的随机数;xb min j和xb max j分别是可行解i中第j个变量的上下界。
计算每个食物源的适应度值fiti,如式(20)所示:
(20)
式中fobj(i)为第i个食物源目标函数值。
选择适应度值较小的食物源构成工蜂种群,另一半食物源构成待工蜂种群。
本文定义指标函数fobj为特征模型输出与实际系统输出的偏差,如式(21)所示。特征模型参数优化问题可描述为在有界闭凸集Ds范围内选择合适的参数值,使得性能指标fobj最小。
(21)
其中
ymod(i,j)=Φmod(j)θ(i,j)
(22)
Φmod(j)=[yact(j-1)yact(j-2)u(j-1)]
(23)
式中ymod(i,j)为j时刻第i个食物源对应的火箭发动机伺服系统特征模型输出;yact(j)为j时刻系统的实际输出;u(j)为j时刻系统的实际输入。
工蜂使用式(24)在食物源附近搜索新的食物源,如果新食物源有相等或更大的适应度值,使用新食物源。否则,保留旧食物源。
xci j=xbi j+βij(xbi j-xbn j)
(24)
式中xci是待选食物源位置;xbi是当前的食物源位置;xbn是邻近食物源位置;βij是[-1,1]之间的随机数。
待工蜂依据概率值Pbi选择一个食物源,如式(25)所示。待工蜂重新按式(24)进行搜索,产生新的待工蜂种群。新的工蜂种群和待工蜂种群结合形成与初始种群大小相同的新种群。
(25)
为了避免丧失种群多样性,当某食物源连续“limit”代不变时,该食物源的工蜂变成侦察蜂,使用式(19)随机确定新的食物源,并与原食物源进行比较,保留适应度值更大的食物源。当算法迭代次数达到预定的最大值,或种群的最优解达到预定误差精度时算法结束。
2.3 火箭发动机伺服系统控制律设计
新型火箭发动机采用位置反馈型伺服控制系统,其主控制量为伺服机构线位移,通过伺服机构线位移推动喷管摆动,进而产生推力矢量控制火箭姿态运动,伺服控制律见式(26),图3为伺服控制系统结构框图。
uall(k)=u0(k)+u(k)+uI(k)+ud(k)
(26)
(1)前馈跟踪控制律u0(k)
前馈跟踪控制律作用于控制输入前端,用于保持伺服系统线位移输出X2(k)精确跟踪线位移指令Xc(k)。引入前馈控制不影响系统的稳定性,同时可改善系统的动态特性,加快响应速度。特征模型反映了实际被控对象的动态特性,伺服控制系统的期望指令跟踪动态特性可表示为式(27):
Xc(k)=α1(k)Xc(k-1)+α2(k)Xc(k-2)+
(27)
式中α1(k)、α2(k)、β0(k)为特征模型参数。
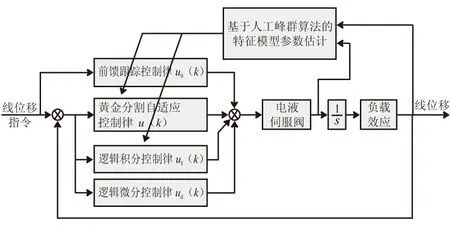
图3 火箭发动机位置反馈型伺服控制系统框图Fig.3 Structure diagram of position servo system of rocket engine
α2(k)Xc(k-2)]
(28)

(29)
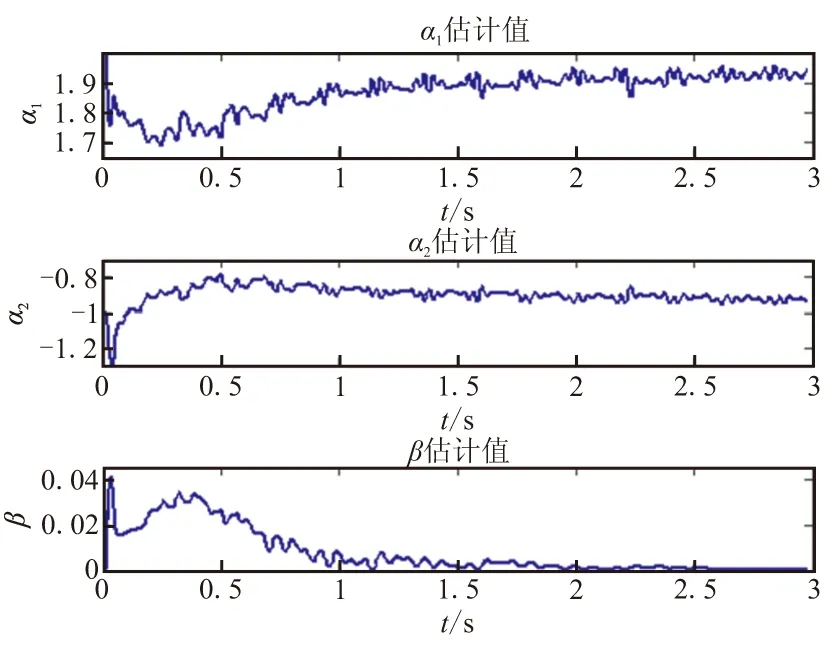
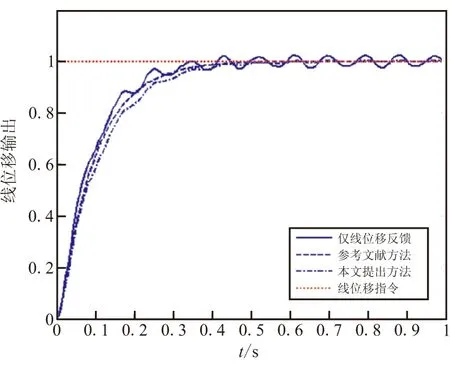
其中,0 (2)黄金分割自适应控制律u(k) 实际工程应用的控制器必须首先保证系统的稳定性。控制系统启动阶段由于输入输出数据量较少,参数估计误差较大,经典的最小方差自校正控制律不能保证控制系统的过渡过程品质,甚至不能保证系统稳定。文献[7]在最小方差控制律基础上,引入黄金分割加权系数,给出了黄金分割自适应控制律u(k)。文献[9]中定理1证明了当特征模型参数α1(k)、α2(k)、β0(k)属于有界闭凸集Ds时,如式(30)所示的黄金分割自适应控制律能保证特征模型参数未收敛于真值条件下,未知参数线性定常系统闭环稳定。黄金分割自适应控制律是火箭发动机伺服系统控制律的核心,保证了控制系统的稳定性和对参数估计误差的鲁棒性。 (30) 式中e(k)为跟踪误差;l1=0.382;l2=0.618。 (3)逻辑积分控制律uI(k) 积分控制律用于消除控制系统跟踪误差,改善稳态跟踪特性,如式(31)所示: (31) 经典积分控制律系数kI仅随系统状态变化,而不随系统跟踪误差e(k)变化。文献[7]提出的逻辑积分控制律根据系统运行状态自动改变控制参数k1,消除系统跟踪静差,避免积分饱和现象。逻辑积分控制律参数kI如式(32)所示: (32) 式中k2>k1>0;Δ为一小正数。 当跟踪误差e(k)增大时,使用逻辑积分系数k2快速降低误差,当输出误差减小时,使用逻辑积分系数k1避免误差反向增大。 (4)逻辑微分控制律ud(k) 微分控制律用于提高系统阻尼比,改善控制系统动态性能,如式(33)所示: (33) 与逻辑积分控制律类似,文献[7]提出的逻辑微分控制律可根据控制动态性能要求自动改变控制参数kd,如式(34)所示。在位置保持或跟踪控制中,逻辑微分系数kd随跟踪误差|e(k)|的减少而增大,当跟踪误差|e(k)|较大时,控制系统阻尼作用较小,以实现指令快速跟踪,当跟踪误差|e(k)|较小时,控制系统阻尼作用较大,以抑制振荡。 (34) 3.1 火箭发动机伺服系统控制器参数设置 通过数字仿真验证基于特征模型的火箭发动机伺服控制系统性能,本文研究的新型火箭发动机最大谐振频率约为120 rad/s。因此,伺服系统最小等效时间常数Tmin≈0.004 s。取参数ηmax=1/3,可得控制周期Δt<0.001 4 s,这里选定Δt=0.001 s。 综合考虑使用人工蜂群算法估计特征模型参数的精度及数值计算速度,选定食物源数量Ne为20,判定食物源耗尽的“limit”代数为100,最大迭代次数为500,计算性能指标fobj所需数据长度N为1 000。 选定发动机伺服系统前馈跟踪控制律中平滑系数为f=0.5,逻辑积分控制律参数为k1=1,k2=3,逻辑微分控制律参数为d=0.5,M=10。 3.2 仿真结果 图4为发动机特征模型与实际系统输出值误差变化曲线,由于特征模型参数估计初始阶段数据量较少,特征模型与实际系统输出值误差较大。随着数据量的增加,输出值误差收敛于零。此时,特征建模与实际对象满足输出等价要求。图5所示为发动机特征模型参数α1、α2、β0估计值变化曲线。由图5可知,当输出值误差收敛于零时,特征模型参数变化趋于稳定,收敛于有界闭凸集Ds内,验证了特征模型参数估值范围的正确性。 图4 特征模型与实际系统输出值误差曲线Fig.4 Output error of characteristic model and actual system 图5 特征模型参数估计值曲线Fig.5 Parameter estimation of characteristic model 文献[5]讨论了位置反馈型火箭发动机伺服控制器的经典构型,该构型采用线位移反馈和动压反馈,同时针对双谐振点负载特性引入两个陷波滤波器。图6和图7为经典火箭发动机伺服控制方法与本文提出方法的单位阶跃响应对比结果。 图6所示为分别采用参考文献方法与本文控制方法的单位阶跃响应曲线,该仿真实验使用仅线位移反馈控制方案作为性能对照组。由图6可知,仅引入线位移反馈时,由于发动机谐振负载特性的影响,系统不能精确跟踪线位移指令,输出响应曲线振荡明显。采用参考文献方法和本文提出方法的伺服控制系统均能精确跟踪指令,动态特性较好。 工程中,通过实验测定的发动机谐振负载特性与实际工作状态的发动机谐振负载特性存在一定差别,图7所示为谐振负载特性参数偏差条件下,分别采用参考文献方法与本文控制方法的单位阶跃响应曲线。由图7可知,采用参考文献方法的伺服控制系统输出响应曲线振荡明显,这是由于经典伺服控制系统设计依赖于精确的数学模型,当模型发生偏差时会影响到控制系统性能。采用本文提出方法的伺服控制系统能精确跟踪线位移指令,动态特性较好,说明本文提出的发动机伺服系统控制方法具有较强的鲁棒性。 图6 发动机伺服控制系统单位阶跃响应曲线Fig.6 Unit step response of engine servo control system 图7 参数偏差条件下伺服控制系统单位阶跃响应曲线Fig.7 Unit step response of servo control system under the condition of parameter deviation (1)基于特征模型理论设计了火箭发动机伺服控制系统,解决了双谐振点负载特性发动机控制问题,实现了发动机对线位移指令的精确跟踪和对双谐振点负载效应的有效抑制,控制律形式简单,阶数较低,易于工程实现。 (2)数字仿真结果表明该火箭发动机伺服控制系统指令跟踪性能良好,动态特性满足要求,对于谐振负载特性参数偏差具有较强的鲁棒性,说明本文提出的基于特征模型的火箭发动机伺服系统控制方案是切实可行的。 [1] 邹俊,傅新,杨华勇,等.自适应交互PID在液压伺服系统中的应用[J].机械工程学报,2006,42(11):179-183. [2] Meng tang,Liu chen.The system bandwidth analysis in electro-hydraulic servo system with PDF control[C]//5th Asian Control Conference,2004,3:1737-1745. [3] Jung-ho Kwon,Tae-hyeong Kim,Ji-seong Jang,et al.Feedback linearization control of a hydraulic servo system[C]//SICE-ICASE International Joint Conference,2006:455-460. [4] Hamid Roozbahani,Wu Hua-peng,Heikki Handroos.Real-time simulation based robust adaptive control of hydraulic servo system[C]//Proceeding of IEEE International Conference on Mechatronics.2011:779-784. [5] 尹传威,赵守军,陈克勤.双谐振点发动机推力矢量控制伺服机构算法优化研究[J].导弹与航天运载技术,2013,324(1):21-26. [6] 蔡璞,许化龙,夏克寒.导弹液压伺服系统中陷波器的原理与设计[J].导弹与制导学报,2006,26(2):148-149. [7] 吴宏鑫,胡军,解永春.基于特征模型的智能自适应控制[M].北京:中国科学技术出版社,2009. [8] 吴宏鑫,王迎春,邢琰.基于智能特征模型的智能控制及应用[J].中国科学(E辑),2002,32(6):805-816. [9] 解永春,吴宏鑫.黄金分割在自适应鲁棒控制器设计中的应用[J].自动化学报,1992,18(2):177-185. [10] 吴宏鑫.全系数自适应控制理论及其应用[M].北京:国防工业出版社,1990. [11] Karaboga D,Basturk B.On the performance of artificial bee colony (ABC) algorithm[J].Applied Soft Computing,2008,8(1):687-697. [12] Seeley T D.The Wisdom of The Hive:The Social Physiology of Honey Bee Colonies[M].Harvard University Press,Cambridge,United Kingdom,1995. [13] Teodorovic D,Dell’Orco M.Bee colony optimization-a cooperative learning approach to complex transportation problems[J].Advanced OR and AI Methods in Transportation,2005:51-60. [14] Luo J,Wang Q,Xiao X H.A modified artificial bee colony algorithm based on converge-onlookers approach for global optimization[J].Applied Mathematics and Computation,2013,210(20):10253-10262. (编辑:吕耀辉) Servo system controller of rocket engine based on Characteristic model FAN Yao1,LI Liang2,QI Peng3,REN Zhang1,WANG Yuan-zhi4 (1.Science and Technology on Aircraft Control Laboratory,Beihang University,Beijing 100191,China;2.Shanghai Electro-Mechanical Engineering Institute,Shanghai 201109,China;3.The Second Artillery Representative Office in the Fourth Academy of CASC,Xi'an 710025,China;4.Unit 96630,The Chinese People's Liberation Army,Beijing 102200,China) Servo system controller based on characteristic model was proposed for the new high-thrust rocket engine.Firstly,the characteristic modeling method was introduced and the range of parameters was discussed. Secondly,artificial bee colony algorithm was employed to estimate the characteristic model parameters of servo system in real time under the condition of equivalent output of characteristic model and actual system.Finally,golden section adaptive control law was introduced to stabilize the close-loop system in the process of parameters estimation,feedforward tracking control law,logical integral and logical derivative control law were also used to improve the performance of servo system.Simulation results demonstrate that the servo system controller can guarantee the accurate tracking of command and robustness to model uncertainty. rocket engine;servo system;characteristic model;artificial bee colony algorithm;golden section adaptive control law 2014-05-10; :2014-08-12。 国家自然科学基金(91116002;91216034;61333011;61121003)。 樊垚(1987—),男,博士,研究方向为飞行器制导控制技术。E-mail:vandoc@126.com V433 A 1006-2793(2015)01-0145-06 10.7673/j.issn.1006-2793.2015.01.0283 仿真验证


4 结论
