以特殊角度攻击地面固定目标的圆周导引律①

胡正东，唐雪梅，王月平

(复杂地面系统仿真重点实验室，北京 100012)



以特殊角度攻击地面固定目标的圆周导引律①

胡正东，唐雪梅，王月平

(复杂地面系统仿真重点实验室，北京 100012)

针对某些导弹以特殊角度攻击地面固定目标的任务要求，提出了一种仅利用视线角测量信息就能实现末速方向控制的圆周导引律。该导引律的基本思想在于控制导弹沿着一系列由导弹和目标的实时位置及要求的命中点角度所确定的圆弧飞行。利用简单的几何原理即可快速解算出各时刻所需要的速度倾角，并将其转换成制导指令。仿真结果表明，与典型的最优导引律相比，圆周导引律更适合于过顶迂回攻击的情况，且受制导周期的影响较小，但受制导指令时延的影响较大。

末速方向控制；圆周导引律；几何原理；最优导引律；过顶迂回攻击

0 引言

对某些精确制导武器，不仅希望获得最小脱靶量，还希望能以特定的速度方向命中目标，从而最大限度地发挥战斗部效能，取得最佳毁伤效果，这就对导引任务的实现增加了终端落角约束。显然，经典的比例导引律难以满足这一要求。

自从Kim和Grider首次在机动弹头再入制导的研究中引入落角约束问题以来，一些学者针对不同的应用背景，根据不同的理论方法提出了多种具有终端角度约束的导引律。利用线性二次最优控制理论，文献[1]推出了具有角速率反馈形式的最优导引律，文献[2]推出了具有角度反馈形式的最优导引律，两种导引律都能满足落角约束，但前者精度更高；文献[3]通过构造Lyapunov函数设计出一种带落角限制的虚拟目标比例导引律；文献[4]利用线性化近似，将具有角度约束的平面交会问题转化为数值控制问题，落角约束作为惩罚函数来处理；文献[5]在经典比例导引律基础上通过增加时变偏差项来处理角度约束，但前提是导弹速度为常值；文献[6-9]则讨论了变结构控制理论在制导律设计中的应用；文献[10]将最优导引律和变结构导引律相结合推出一种复合导引律，利用RBF神经网络自适应调节增益系数有效地避免了纯变结构导引律中的制导指令抖振问题。

目前绝大多数具有终端角度约束的导引律都要求导引头能提供视线距离、视线角速率等信息，这极大限制了导引头的选取范围。本文给出一种打击地面固定目标的圆周导引律，在无线性化假设和速度恒定要求的前提下，该导引律仅利用视线角测量信息就能实现末速方向控制，而且其弹道的几何曲线特性使得导弹非常适合对敌方反斜面目标实施过顶迂回攻击。

1 导引段数学模型

导引段定义为导弹在制导系统作用下飞向目标直至落地的全过程。为方便研究，本文仅考虑纵向平面内的运动，故无推力作用的导弹质心运动方程可写为[1]

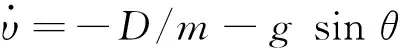
(1)

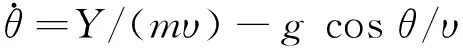
(2)

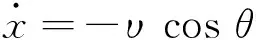
(3)

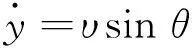
(4)

式中υ为导弹速度；θ为速度倾角；x和y分别为导弹相对目标的水平位置和高度；m为导弹质量；g为引力加速度；D和Y分别表示阻力和升力，它们是速度υ和攻角α的函数。

2 圆周导引律

圆周导引律基本思想：假定在每一时刻，导弹和目标的位置均处在同一个圆上，且所需的终端速度方向位于目标点的切线上(则每一时刻均可确定唯一的圆)，因此只要控制导弹沿着这一系列圆弧飞行，即可在命中目标的同时满足撞击角度要求。

理想情况下，若导弹速度大小恒定且机动能力足够强，不难推断出该圆的形状基本保持不变，导弹的飞行轨迹具有良好的几何特性。但实际上由于外力的作用和控制能力的限制，圆弧的形状在飞行过程中必然发生变化，导弹此时的弹道特性如何、能否满足命中点参数的要求将是本文研究的重点。

本节首先推导圆周导引律的数学公式，分迎面攻击和过顶迂回攻击2种情况进行讨论。

2.1 迎面攻击

迎面攻击是指导弹在飞行过程中不出现飞过目标的情况。根据弹道几何特性，导弹的飞行阶段可能为“升弧段→降弧段”或仅存在“降弧段”。

2.1.1 升弧段

迎面攻击的升弧段示意图如图1所示。图中，P、T分别表示导弹位置和目标位置；θf为给定的末速方向(-90°≤θf<0)；O表示由P、T和θf确定的圆心；q为视线角；θR为制导所需的速度倾角；υR和υf分别为沿θR和θf方向的速度矢量，且均为圆弧的切线。显然，对于升弧段有θR≥0。

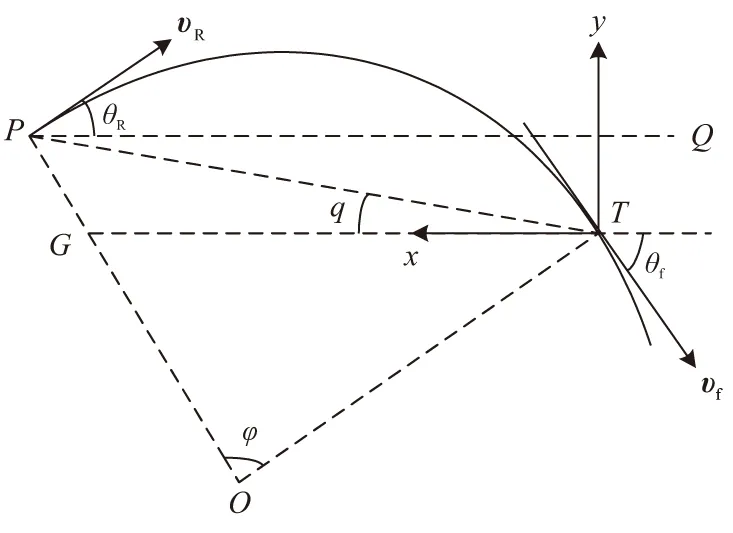
图1 迎面攻击的升弧段示意图Fig.1 Ascending section in head-on attack

由OT⊥υf，可知∠GTO=90°-|θf|，则

∠OGT=180°-∠GTO-∠TOG

=90°+|θf|-φ

(5)

又OP⊥υR，且∠GPQ=∠OGT，故

θR=90°-∠GPQ=φ-|θf|

(6)

在等腰ΔPOT中存在如下关系：

(90°-|θf|+q)×2=180°-φ

(7)

整理可得

φ=2|θf|-2q

(8)

将上式代入式(6)，并注意到θf<0，即有

θR=-(2q+θf)

(9)

2.1.2 降弧段

降弧段对应于弹道中θR<0的部分，如图2所示。

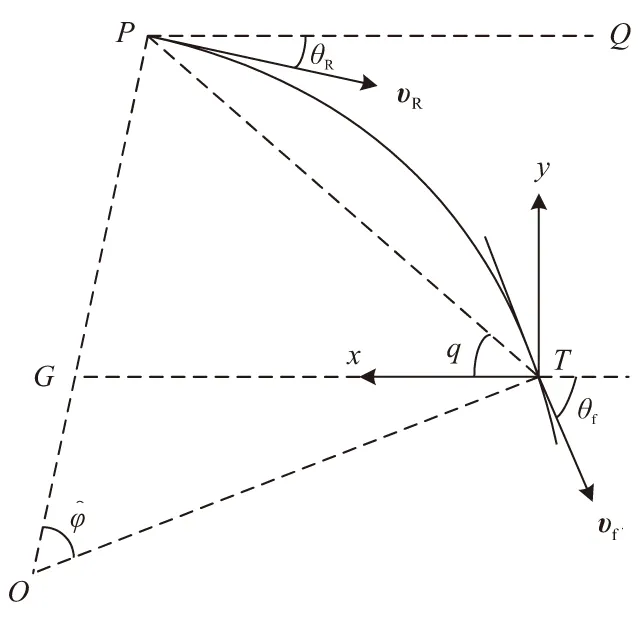
图2 迎面攻击的降弧段示意图Fig.2 Descending section in head-on attack

显然，与升弧段的推导类似，有

∠GPQ=∠OGT=90°+|θf|-φ

(10)

φ=2|θf|-2q

(11)

由OP⊥υR，可知

|θR|=∠GPQ-90°

(12)

综合以上各式，且注意到θf<0，θR<0，不难得到

θR=-(2q+|θf|)

(13)

2.2 过顶迂回攻击

过顶迂回攻击是指导弹在飞行过程中绕到目标后方再下压攻击目标的情况。与迎面攻击相比，过点迂回攻击提高了打击的突然性，且有效增加了对敌方反斜面目标的打击能力，如图3所示。

根据弹道的几何特性，导弹的飞行阶段可能为“升弧段→降弧段→瞄准段”或“降弧段→瞄准段”。

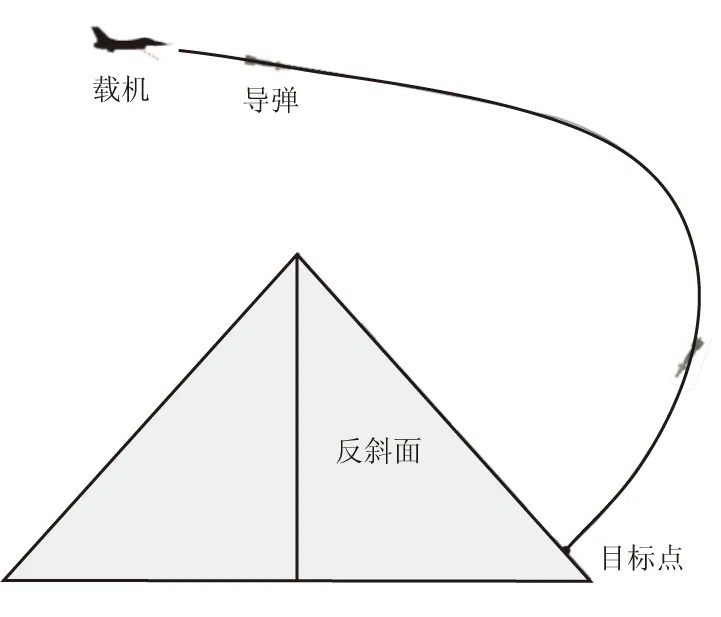
图3 过顶迂回攻击反斜面目标的情况Fig.3 Overhead-attack on back-slope target

2.2.1 升弧段

升弧段对应于弹道中θR≥0的部分，如图4所示。注意对于过顶迂回攻击情况，有-180°<θf<-90°。

图4 过顶迂回攻击的升弧段示意图Fig.4 Ascending section in overhead-attack

由OT⊥υf，不难得到

|θf|=(q-∠OTP)+90°

(14)

在等腰ΔPOT中，显然有

∠OTP=∠OPT=(180°-φ)/2

(15)

将上式代入式(14)，可得

φ=2|θf|-2q

(16)

由于OP⊥υR，故

∠OPT+∠TPQ+θR=90°

(17)

注意到∠TPQ=∠PTG=q，θf<0，故由式(15)～式(17)可推得

θR=-(2q+θf)

(18)

2.2.2 降弧段

降弧段对应于弹道中-90°≤θR<0的部分，如图5所示。

图5 过顶迂回攻击的降弧段示意图Fig.5 Descending section in overhead-attack

在四边形POGT中，由OP⊥PG和OT⊥TG可知

∠PGT=180°-φ

(19)

由于PG和GT均为切线段，故可知PG=GT，从而在等腰ΔPGT中：

∠GPT=(180°-∠PGT)/2=φ/2

(20)

注意到∠TPQ=q，从而不难得到

|θR|=∠TPQ-∠TPG=q-φ/2

(21)

又由于∠OTP=(180°-|θf|)+q-90°，故在等腰ΔPOT中：

φ=180°-2×∠OTP=2|θf|-2q

(22)

将上式代入式(21)，并注意到θf<0，θR<0，最终可得

θR=-(2q+θf)

(23)

2.2.3 瞄准段

瞄准段对应于弹道中θR<-90°的部分，如图6所示。

显然，瞄准段θR的推导过程与降弧段的情况完全一致，因此可直接写出：

θR=-(2q+θf)

(24)

2.3 制导指令生成

从迎面攻击与过顶迂回攻击两类情况的讨论可以看出，为保证导弹沿给定的末速方向命中目标，始终需要满足：

θR=-(2q+θf)

(25)

可以看出，圆周导引律所需的制导信息仅包括视线角q。理想情况下，导弹在每个制导时刻调整自身的速度倾角θ=θR，从而保证精确命中目标；但实际上飞行状态并不可能瞬时改变，它需要根据误差信号产生制导指令、并经控制系统作用最终由弹上的执行机构调整飞行姿态来完成。

在各制导时刻令Δθ=θR-θ(此处θ为实际飞行参数)，Δt为时间步长，则由式(2)近似可得

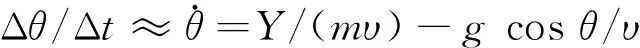
(26)

于是，由上式即可解出满足速度倾角修正要求的攻角α′；在考虑过载限制和最大攻角限制后，即可获得实时的制导指令αcom。

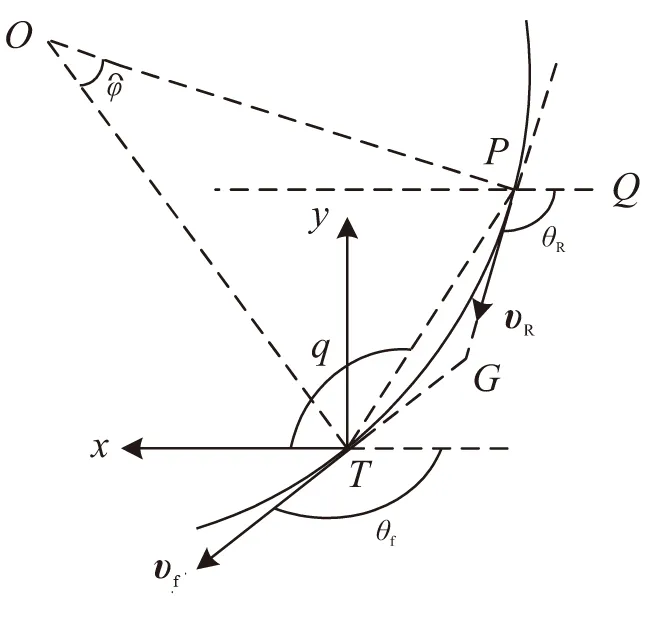
图6 过顶迂回攻击的瞄准段示意图Fig.6 Targeting section in overhead-attack

3 仿真分析

3.1 制导性能初步验证击

下面首先通过仿真来验证圆周导引律的基本性能。设导弹初始时刻位置为x0= 15 km，y0= 15 km，初始速度为υ0= 1 km/s，最大攻角为20°，最大法向过载为15，弹道仿真步长取0.01 s。考虑以下4种情况：

情况A：θ0=20°，θf=-60°；

情况B：θ0=-20°，θf=-60°；

情况C：θ0=20°，θf=-120°；

情况D：θ0=-20°，θf=-120°。

上述4种情况下圆周导引律的制导效果如表1所示，相应的弹道曲线见图7。

表1 不同情况下的制导效果Table 1 Guidance results in four cases

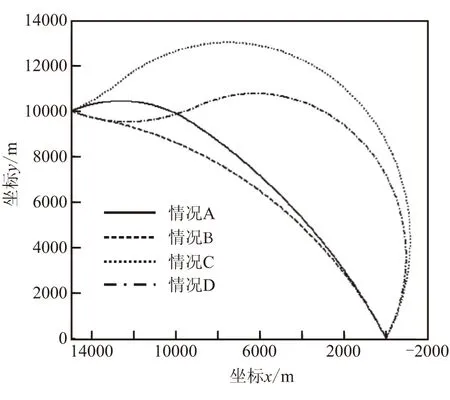
图7 导引弹道曲线Fig.7 Guidance trajectory curves

从仿真结果可看出，圆周导引律能够在保证较高命中精度的同时，满足给定的终端速度方向约束，且弹道曲线较为光滑，未超出过载限制和机构限制。此外，通过对比前2种情况与后2种情况的制导效果可知，在初始条件相同时，过顶迂回攻击比迎面攻击的弹道弯曲得多，飞行路径的增加必然导致飞行时间的大幅增加和落点速度的显著降低，但制导精度并无太大变化。

3.2 与最优导引律的比较

文献[1]给出的带落角约束的最优导引律形式为(仅考虑纵向平面)

(27)

下面分别从可能影响制导效果的几个方面来比较圆周导引律(用G1表示)与上述最优导引律(用G2表示)的性能。

3.2.1 末速方向的影响

取θ0=-20°，观察不同末速方向约束对两类导引律制导效果的影响，见表2。

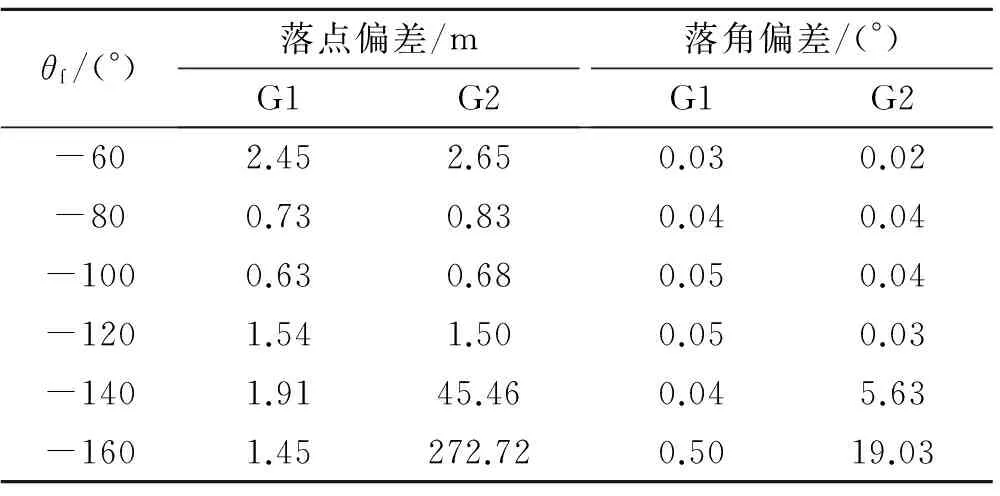
表2 不同末速方向下的制导效果Table 2 Guidance effect in different directions

由表2可知，两类导引律在终端速度倾角靠近-90°时均具有良好的制导性能，向其两侧变化则制导效果有所下降；但是对于大角度过顶迂回攻击的情况，圆周导引律仍能保持较高的制导精度，而最优导引律的制导性能则急剧恶化——图8给出了恶化的原因，这是由于最优导引律的攻角在大角度过顶迂回攻击(θf=-140°和θf=-160°)时易出现饱和的缘故。

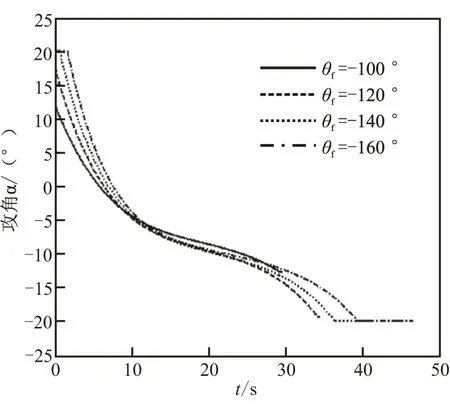
图8 最优导引律的攻角变化曲线Fig.8 Attack angle curve under optimal guidance law

3.2.2 制导周期的影响

根据前面的讨论可知，最优导引律在过顶迂回攻击时的制导性能往往表现得不尽如人意，因此在以下的比较中均取θ0=-20°，θf=-60°。制导周期影响指令更新频率，表3给出了不同制导周期下的制导效果。

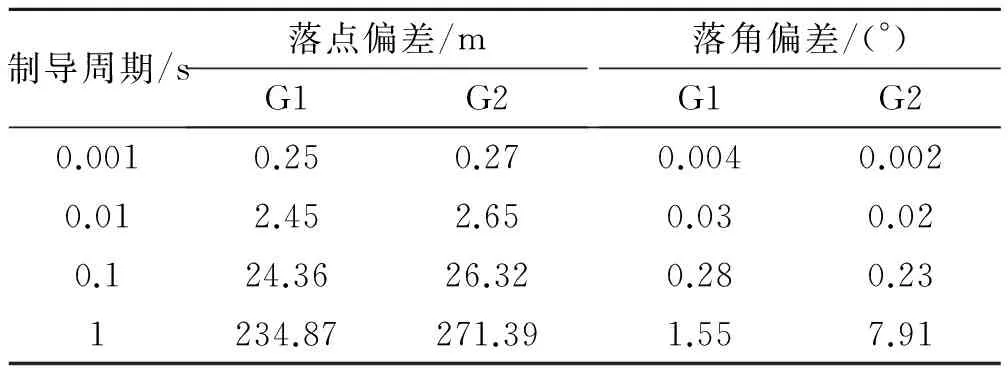
表3 不同制导周期下的制导效果Table 3 Guidance effect in different cycles

由表3可知，随着制导周期的增加，2类导引律的制导效果均出现下降趋势，但最优导引律相对更差。

3.2.3 制导指令时延的影响

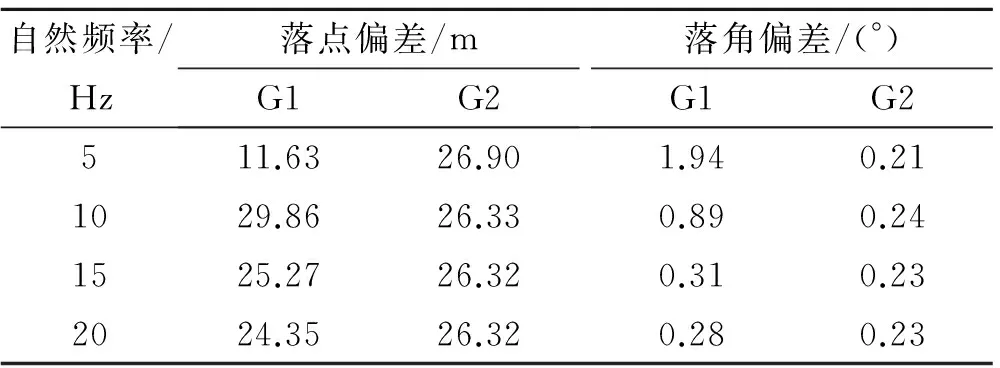
表4 不同指令时延下的制导效果Table 4 Guidance effect in different delays

可以看出，在自然频率为5～20 Hz的范围内，最优导引律的制导效果几乎不发生变化，而圆周导引律的变化则显著得多，这表明制导指令时延对圆周导引律的影响要大一些。此外，随着自然频率的减小(即制导指令的响应速率变慢、时延增加)，圆周导引律的制导效果总体上趋于变差——需要说明的是，对于自然频率为5 Hz的情况，由于存在控制量的抖振，如图9所示，抖振会极大地降低控制系统的性能，甚至破坏控制器件，因此这并不能说明自然频率越小越好。综上所述，圆周导引律对控制系统的灵敏性提出了更高的要求。

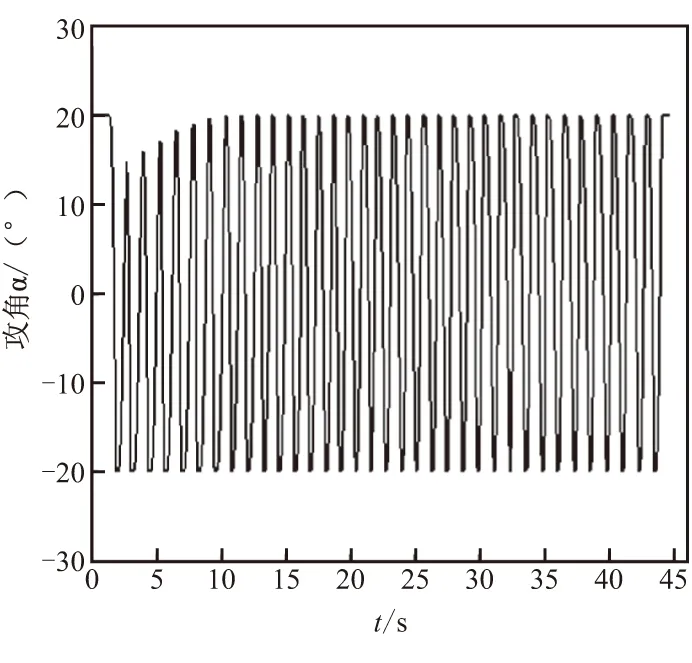
图9 圆周导引律的攻角抖振曲线Fig.9 Buffeting curve of angle of attack

3.2.4 气动系数误差的影响

气动系数误差主要由制造工艺误差及地面风洞试验偏差造成，它会引起制导指令的计算误差并给制导精度带来一定的影响。取不同的气动系数误差百分比，观察制导效果变化情况，如表5所示。

由表5可知，在气动系数存在一定误差的情况下，两类导引律仍能保持较高的制导精度，这主要是因为它们均采用了闭环制导方式，制导指令的实时修正削弱了气动系数误差的影响。

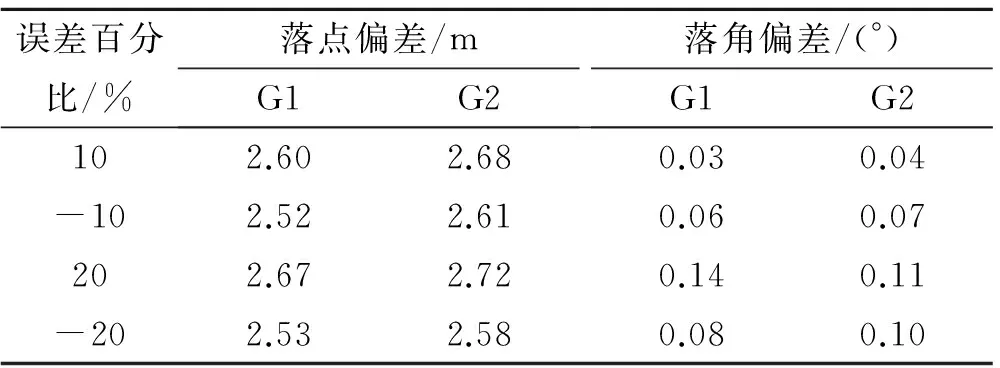
表5 不同气动系数误差下的制导效果Table 5 Guidance effect in different aerodynamic errors

3.2.5 水平风的影响

不同水平风速对制导效果的影响见表6。

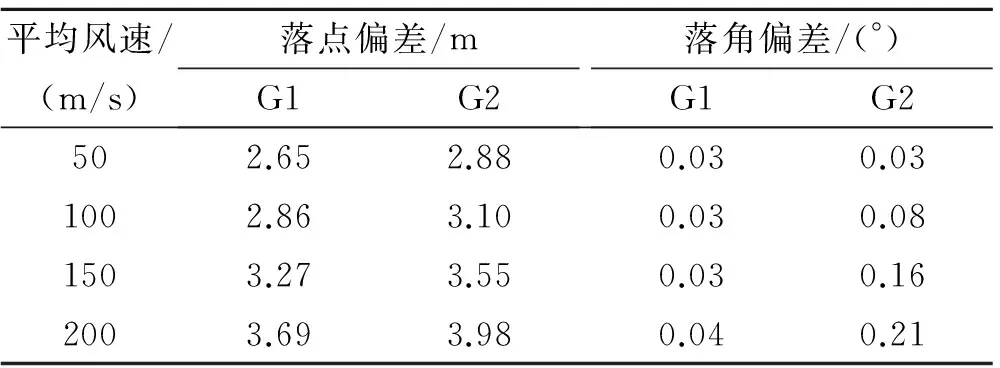
表6 不同平均风速下的制导效果Table 6 Guidance effect in different wind speed

可以看出，水平风对2类导引律制导效果的影响基本相当；随着风速的增加，制导精度均出现下降趋势——由于仿真中导弹速度较大且采用闭环制导修正，故此处制导精度变化并不是非常显著。

4 结论

(1)圆周导引律能够在保证较高命中精度的同时，满足给定的终端速度方向约束。

(2)与典型的最优导引律相比，圆周导引律更适合于过顶迂回攻击的情况，且受制导周期的影响较小，但受制导指令时延的影响较大，至于气动系数误差和水平风的影响，两者基本相当。

(3)从所需测量信息的角度看，圆周导引律仅需视线角信号，而上述最优导引律则需要视线角及其变化率、视线距离及其变化率，显然，前者极大地扩展了导引头的选取范围。

[1] 赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997.

[2] 陈海东,余梦伦,董利强.具有终端角度约束的机动再入飞行器的最优制导律[J].航天控制,2002(1):6-11.

[3] 顾文锦,雷军委,潘长鹏.带落角限制的虚拟目标比例导引律设计[J].飞行力学,2006,24(2):43-46.

[4] Song T L,Shin S J,Cho H.Impact angle control for planar engagements[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(4):1439-1444.

[5] Kim B S,Lee J G,Han H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.

[6] 胡正东,张皓之,蔡洪.带落角约束的再入机动弹头的变结构导引律[J].系统工程与电子技术,2009,31(2):393-398.

[7] 宋建梅,张天桥.带末端落角约束的变结构导引律[J].弹道学报,2001,13(1):16-20.

[8] 周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002.

[9] 刘永善,贾庆忠,刘藻珍.电视制导侵彻炸弹落角约束的变结构导引律[J].弹道学报,2006,18(2):9-14.

[10] 胡正东,郭才发,蔡洪.带落角约束的再入机动弹头的复合导引律[J].国防科技大学学报,2008,30(2):21-26.

(编辑：吕耀辉)

Circular guidance law against stationary target with specified impact angle

HU Zheng-dong，TANG Xue-mei，WANG Yue-ping

(Science and Technology on Complex Land Systems Simulation Laboratory，Beijing 100012，China)

Aiming at the problem that impact on the ground stationary target with specified angle is required for some guided missiles,a circular guidance law which only uses the line-of-sight angle information for terminal velocity direction control was derived.The idea of this approach is to guide the missile following a series of circular arcs determined by the specified impact angle and the real-time position of the missile and the target.Based on the simple geometrical principle,the required velocity inclination angle can be quickly worked out,which is then used for guidance command generation.Simulation results show that compared with the typical optimal guidance law,the circular guidance law presented is more favorable to the case of overhead-attack and is less affected by guidance periods,but is more affected by guidance order delay.

terminal velocity direction control；circular guidance law；geometrical principle；optimal guidance law；overhead-attack

2013-01-21；

：2013-03-07。

863项目(2012AA0802)。

胡正东(1982—)，男，博士，研究方向武器装备论证仿真。E-mail：waixitu@126.com

V448

A

1006-2793(2015)01-0001-06

10.7673/j.issn.1006-2793.2015.01.001