滚珠丝杠进给系统热变形研究*

王全宝 肖 宁 余光怀 李江艳

(沈机集团昆明机床股份有限公司，云南 昆明 650203)

随着机床向高效、高速、高精度方向迅速发展，对机床的各项性能提出了更高的要求。高速切削机床随着机床转速和工件加工质量的提高，切削深度一般都比较小，切削力不大，因而机床受力变形对加工精度的影响变小，而热变形影响的比重变大。在机械加工过程中，进给系统在各种热源的影响下产生热变形，致使进给系统产生位置误差，从而影响机床的运动精度，因而对滚珠丝杠热变形进行研究有着重要的意义。本文通过有限元数学模型的建立进行温度场模拟试验并与实际工况下温度传感器测试结果进行对比分析，验证了有限元法的正确性;然后根据实际工况测试结果对有限元边界条件进行修正，并进行系统温度场优化设计，降低了系统的热平衡温度，减小了热变形，提高了滚珠丝杠进给系统的传动精度。

1 滚珠丝杠温度场及热变形数学模型

1.1 滚珠丝杠热源发热量计算

(1)轴承的发热量

滚动轴承的摩擦热主要是由其摩擦力矩产生的，其发热量计算公式如下:

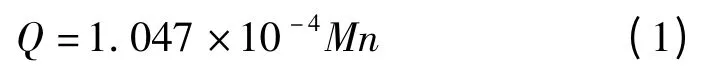
式中:Q 为发热量，W;n 为丝杠的转速，r/min;M 为滚动轴承的摩擦力矩，N·mm，M=M0+M1，M0是与轴承类型、转速和润滑油性质有关的力矩，M1是与轴承所受负荷有关的摩擦力矩［1-2］。

(2)滚珠丝杠副的摩擦转矩的计算

滚珠丝杠副的发热量计算方法和轴承相同，其摩擦力矩计算方法为:

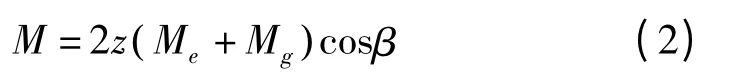
式中:z 为滚动体数目;β 为丝杠滚道的螺旋角，(°);Me为阻力矩［2］;Mg为滑移摩擦力矩［2］。

根据式(1)和(2)就可以求解出滚珠丝杠副的发热量，将其转化为热载荷施加在丝杠进给系统的有限元模型上，可求解丝杠进给系统的温度场。

(3)电动机发热量的计算

电动机的定子和转子的发热来源于电动机的损耗，其发热量为

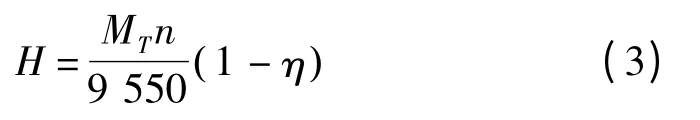
式中:H 为发热量，kW;MT为输出力矩，N·m;n 为电动机转速，r/min;η 为机械效率。

1.2 丝杠热位移计算

滚珠丝杠副在高速运转的情况下，丝杠受到运转时间和运转速度的影响导致温度升高，热变形加剧。滚珠丝杠热位移公式为:

式中，Δ Lθ为热位移量，mm;ρ 为热膨胀系数;θ 为滚珠丝杠温升值;L 为滚珠丝杠长度，mm。

2 有限元分析

针对前面建立的温度场及热变形数学模型，为了验证其正确性，用ANSYS 有限元分析软件对其进行分析。将丝杠系统进行必要的简化，简化原则:(1)去除各螺钉或螺栓孔;(2)由于只分析丝杠系统的热变形情况，不考虑热应力的影响，所以去除结构中的倒角和小台阶;(3)丝杠螺母的结构较复杂，将其简化为一个体积相同的圆筒;(4)将支撑轴承等效为一个圆筒。并对其进行网格划分，得到其有限元模型，如图1所示。

该系统是通过预拉伸使丝杠伸长0.035 mm 来实现对轴承的预紧的，要计算轴承的发热量，首先利用ANSYS 结构分析得出丝杠的轴向拉应力，从而求出轴承的预紧力约为885.48 N。如图2 所示。

滚珠丝杠进给系统热边界条件参数如表1 所示。

根据求得的热载荷加载到其有限元模型上，得到其温度和热变形情况。如图3 所示。

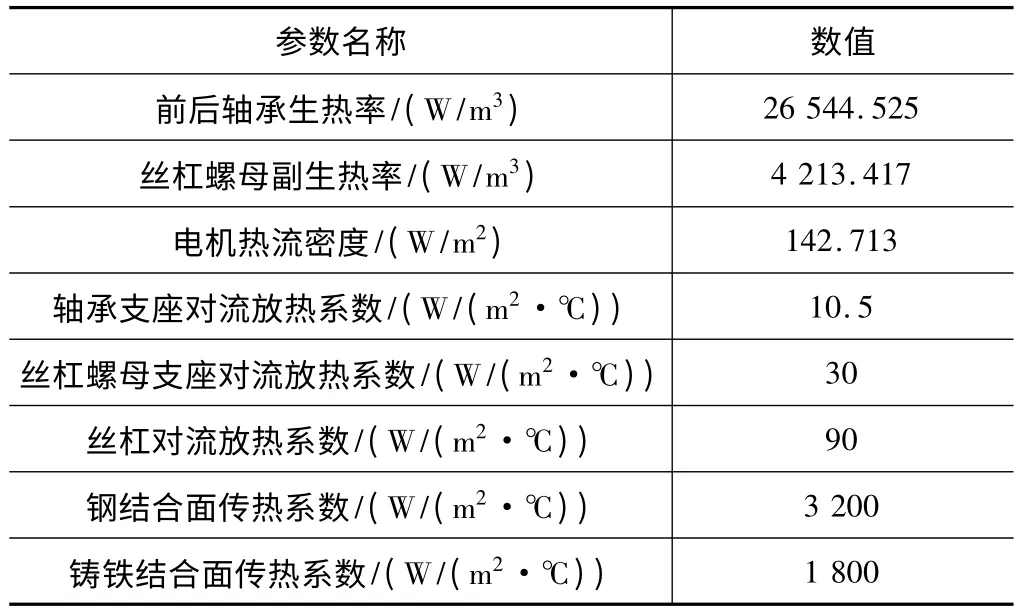
表1 温度场边界条件参数表

整个系统受3 个热源的影响，其温度变化比较复杂，简而言之，整体趋势为两边轴承温升较高，中间丝杠螺母处相对较低，整个系统最高温度在丝杠支撑座处，为24.643 ℃，最低温度为20.008 ℃。

由分析知，丝杠的最大热变形为0.0099 mm，丝杠的整体变形趋势是中间向下凸起，丝杠的最大热变形主要是丝杠的伸长，出现在丝杠的轴承座末端，最大伸长量为0.0052 mm。

3 试验测试

根据工厂经验和红外热像仪测试结果，确定机床进给系统的热源为两端丝杠轴承和滚珠丝杠螺母。

根据机床的实际结构，在丝杠热源处和热源周围布置若干温度传感器对丝杠的热特性进行测试，现场测试图如图6 所示。

布置好传感器之后，让机床进给系统以一定速度在一定行程内空载来回运行，实时观察和记录各传感器所测温度的变化。使用多通道参数测量系统对温度传感器输出信号进行处理，得到各温度传感器的实时曲线图，如图7 所示。

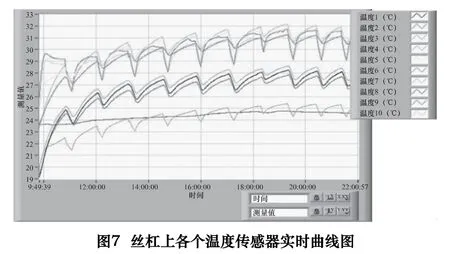
根据试验结果可以看出，丝杠的热源主要来自丝杠轴承和丝杠螺母，丝杠的最低温度为19 ℃，最高温度为32 ℃;通过位移传感器测试出丝杠末端伸长量为0.01961 mm。根据分析和测试结果，设计师可以在机床的设计中采取一些相应的措施来减少丝杠系统的发热量，降低温升，提高丝杠进给系统的运动精度。

4 对比分析与优化设计

4.1 对比分析与边界条件修正

通过有限元分析和试验测试可以得出表2 所示的对比数据。

从表2 可以看出，模拟数据与实际工况数据在最低温度和每℃伸出量两个指标上相符度非常高，说明ANSYS 热位移边界条件设置准确度很高;而最高温度及热伸长量的相符度较低，说明ANSYS 分析中轴承发热量的参数设置不太符合。

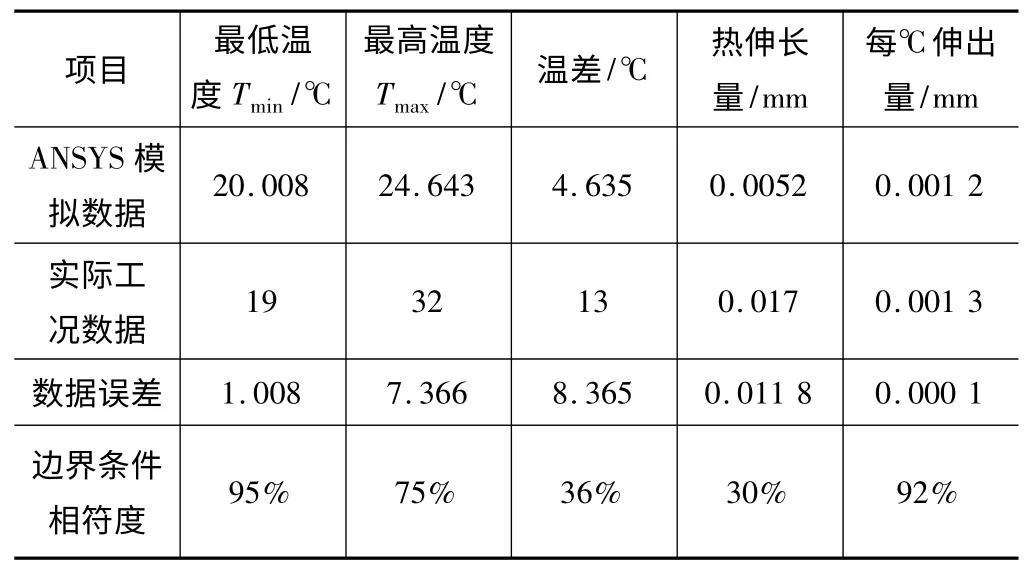
表2 数据对比表

ANSYS 模拟分析过程中并未考虑轴承中心孔同轴度误差、加工装配误差等因素的影响，加之摩擦扭矩是通过经验公式进行计算的，与实际工况有一定差距。为了与实际工况具有更高的相符度，需要修改轴承发热量边界条件再进行分析对比，修改后得到的数据如表3 所示(具体分析测试过程与前文相同，不再累述)。

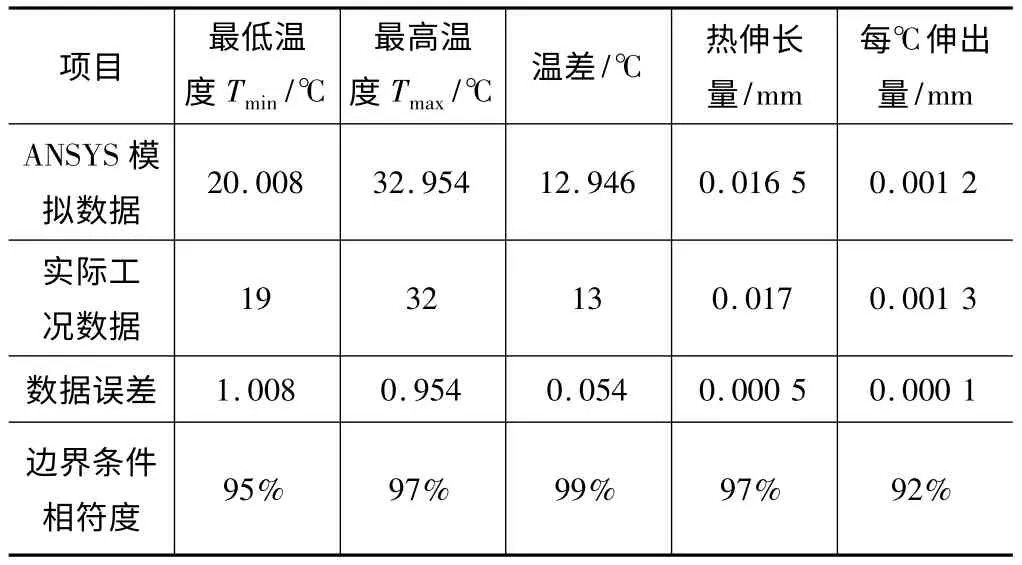
表3 再分析数据对比表

修订轴承发热量边界条件后，模拟数据与实际工况数据相符度均在92%以上，具有很高的工程指导意义，基于该数学模型下进行结构优化设计具有很高的工程应用价值。

4.2 滚珠丝杠传动系统优化设计

从上述分析可以看出，丝杠轴承发热量与丝杠热伸长量呈线性关系，为了得到更小的热伸长、更高的传动精度，采取以下措施进行优化设计:

(1)将成对安装的丝杠轴承之间用隔套隔开，增大轴承散热面积，使得轴承散热更快。

(2)丝杠轴承润滑由脂润滑改进为循环油润滑，油温冷却机冷却的循环油既能充分润滑轴承又能迅速带走滚珠与滚道摩擦产生的热量。

(3)提高前后轴承座的形位精度及相互同轴度要求，减小由于丝杠轴承不同轴产生的额外摩擦扭矩和摩擦热。

(4)优化丝杠轴承、丝杠螺母的预紧力，减小丝杠与螺母滚珠、轴承内外圈与轴承滚珠之间摩擦。

通过上述措施进一步优化后，使用修正后的数学模型进行分析计算得出表4 中数据。

通过优化设计，改善了滚珠丝杠传动系统的温度场，降低了系统的热平衡温度，减小了滚珠丝杠的热伸长量，大大提高了滚珠丝杠进给系统的传动精度。

5 结语

(1)本文首先针对导致丝杠热变形的各热源进行了分析，并对前后轴承以及电动机的发热量进行了计算，建立热变形数学模型，利用ANSYS 软件对丝杠的热变形进行分析。

(2)其次，采用红外热像仪对丝杠高速运转时的发热量进行测试，进一步确定了热源;通过在热源上布置温度传感器测试了各个热源在丝杠运转情况下的温升以及丝杠的热伸长量，修正了ANSYS 数学模型的边界条件设置，完善了数学模型的建立。

(3)再次，通过4 种有效的优化设计措施，降低了滚珠丝杠进动系统的热平衡温度，减小了滚珠丝杠的热伸长量，大大提升了进给系统的传动精度。

(4)本文阐述的“数学模型建立—实际工况验证—边界条件修正—数值模型优化设计”研究方法为机床进给系统设计提供了很好的参考，具有很高的应用价值。

［1］张刚.滚珠丝杠副摩擦力矩测量仪研制及其实验分析［D］.济南:山东大学，2007.

［2］程光仁，施祖康，张超鹏.滚珠螺旋传动设计基础［M］.北京:机械工业出版社，1987:78 -86.

［3］张国智，胡仁喜，陈继刚，等.ANSYS10.0 热力学有限元分析实例指导教程［M］.北京:机械工业出版社，2007:1 -5.

［4］韩晓海.提高加工中心加工精度的方法和途径［J］.杭州机械，1999(3):15 -18.

［5］唐开勇.机床热变形的探讨［J］.昆明理工大学学报，2002，27(3):51 -54.

［6］夏军勇，吴波，胡游民，等.多变化热源下的滚珠丝杠热动态特性［J］.中国机械工程，2008，19(8):955 -958.

［7］缪亚雄，孙蓓蓓.滚珠丝杠系统的热特性建模与分析研究［J］.中国制造业信息化，2008，37(3):46 -48.

［8］王大伟，刘永红.基于有限元法的滚珠丝杠传动过程中的温度场和热变形仿真［J］.计算机辅助工程，2009(2):29 -33.