双馈风力发电机的接入对电力系统功角稳定特性的影响

于灿平，俞巍伟，熊剑青，黄宁吉

(1.国电南京自动化股份有限公司，南京 210032;2.杭州华电江东热电有限公司，杭州 310018)

0 引言

双馈风力发电机(DFIG)是当前风力发电的主流机型，采用双馈异步发电机，与恒速感应风电机组不同的是，DFIG的转子通过1个背靠背的负载变频器与电网相连，变频器容量仅为风电机组总容量的20% ～30%［1-2］，其转子转速可通过转子变频器进行动态调节，使DFIG转子转速能在较大范围内运行，比恒速风电机组提高发电量5%［3］。DFIG转子侧换流器利用转子电流在同步旋转坐标系d轴和q轴的分量控制定子绕组的有功功率和无功功率，实现DFIG有功和无功的解耦控制。

目前，双馈风电机组的接入容量在电力系统总发电容量中占据一定比例，对电力系统的安全、稳定运行具有一定影响。此外，我国风电场大多位于西北地区，煤炭储量丰富，火力发电较为集中，“风火打捆”集中外送势在必行。因此，评估双馈风电机组的接入对电力系统稳定性的影响不仅具有一定的理论研究价值，而且具有一定的实际意义。文献［4-6］研究了风电并网后电力系统的电压稳定性，并取得了一定的成果;文献［7-8］对风电机组接入后系统的小干扰稳定特性进行了相关探讨，研究了风电机组并网后对系统阻尼特性的影响，并分析了相关影响因素;文献［9-15］重点研究了DFIG接入后系统的暂态稳定特性，其中文献［9］研究发现了DFIG和同步发电机的功角摇摆曲线存在2类交点，并将其分别定义为主动交越点和被动交越点，交越点的性质决定了双馈发电机对常规同步发电机的影响;文献［13］基于双馈风电机组接入电网后减少了电网的转动惯量的特性，利用转动惯量的灵敏度分析和暂态稳定指标探讨风电接入后系统的小干扰稳定性和暂态稳定性;文献［14］从有功和无功2个方面分析了风电机组接入系统后对常规同步发电机间功角稳定的影响，指出风电机组的无功控制可以缓解风电机组接入系统后同步发电机组在电网出现不稳定事件时的负担，有利于同步发电机间的功角稳定。上述文献尽管取得了一定的成果，但是仅从仿真方面进行说明，未充分结合理论进行深入分析。

本文对双馈风力发电机功角特性进行定义，推导双馈风电机组的等效外特性，在此基础上研究双馈风电机组接入后单端送电系统的功率特性，进而对双馈风电机组接入后单端系统的暂态稳定特性进行理论分析。分别在减少同步发电机出力及替换同步发电机2种情况下，对DFIG接入后同步发电机的功角稳定特性进行了相关理论分析，最后通过仿真对研究结果进行验证。

1 DFIG运行原理

DFIG采用绕线式异步发电机，定、转子绕组均为三相对称绕组。与普通异步发电机转子侧直接短接不同，DFIG通过与转子绕组相连的电压源换流器进行励磁，其转子转速可以通过改变交流励磁电源的频率进行调节，克服了传统同步发电机必须严格同步的要求，把发电机机械与电气之间的刚性联系变为柔性联系。此外，DFIG具有广泛的稳定运行范围，在任一滑差的运行点上具有与传统同步发电机相同的功角特性方程［16］

式中:Pe为电磁功率;E'为DFIG等效内电势;Us为DFIG机端电压;Xs为DFIG等效电抗;s为转子转差率;δ为DFIG功角。

DFIG在同步旋转dq坐标轴下的电压方程和磁链方程的相量形式如下(定、转子侧绕组参考正方向均按照电动机惯例选取)。

电压方程

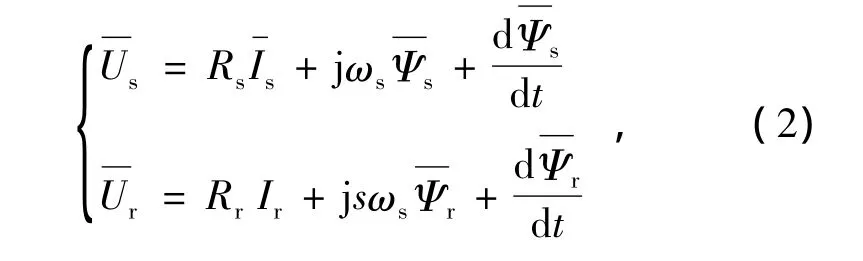
磁链方程

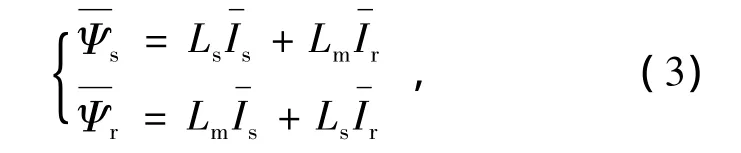
式中:Us为定子电压;Ur为转子电压;Is为定子电流;Ir为转子电流;Ψs为定子磁链;Ψr为转子磁链;Rs为定子电阻;Rr为转子电阻;ωs为同步角速度;s为转差率;Ls为定子自感;Lr为转子自感;Lm为定转子之间的互感。

由式(2)可得

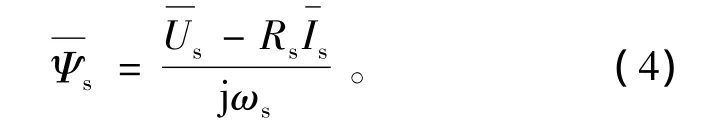
由式(3)可得

将式(5)代入式(4)并整理得

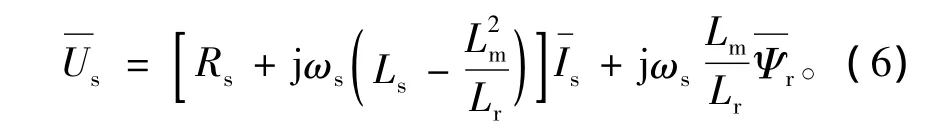
式(6)即为DFIG的戴维南等效电路，如图1所示。

图1 DFIG戴维南等效电路

MW级DFIG的定子电阻较小，可忽略，则等效电抗为

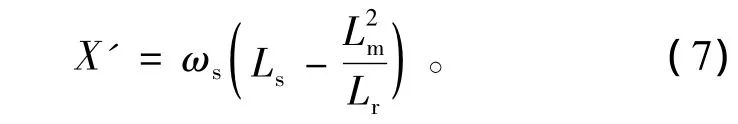
定子电压为

等效内电势为

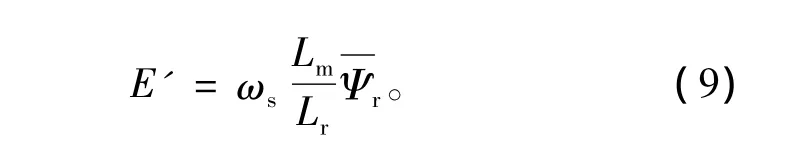
将式(7～9)代入式(1)得出

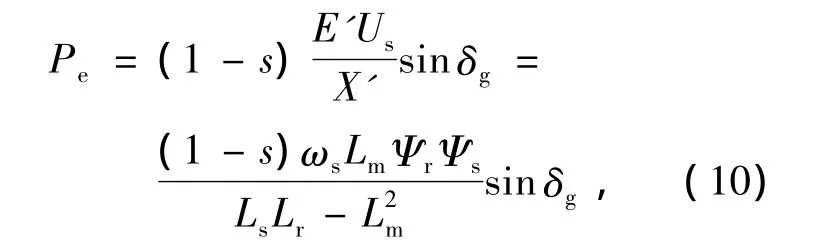
式中:δg为定、转子磁链空间矢量之间的角度差。

2 DFIG接入后同步发电机功角稳定性

风电机组的接入势必要替换掉部分常规机组的出力，一种是以同等容量的风电机组替换掉常规同步发电机，另一种是将各同步发电机组减出力运行，以满足系统对风电机组出力的需求。

2.1 等容量DFIG替换同步电机的功角稳定特性

电力系统发生故障导致DFIG机端电压跌落时，DFIG内部将会发生一系列的动态变化，其中定子磁链的变化过程是分析DFIG动态响应过程的关键。根据式(3)将定子电流用定子磁链和转子电流表示代入式(2)中的定子电压方程，整理得出

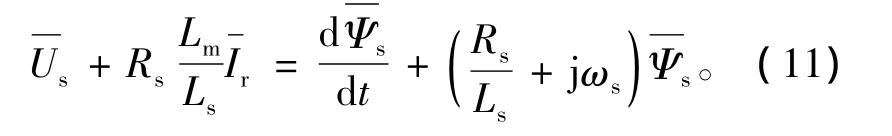
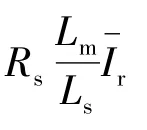
由式(12)得DFIG暂态电流

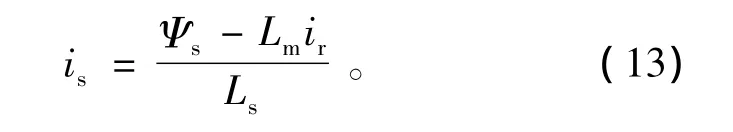
将式(12)代入式(13)，同时取转子暂态电流为指令值可得

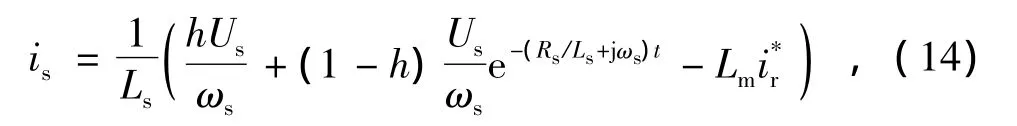
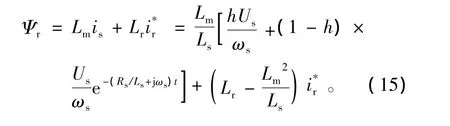
双馈风电机组具有有功、无功解耦控制能力，其常运行在恒功率因数运行方式下，控制无功功率输出为0，且DFIG对系统几乎不体现出转动惯量，因此，DFIG主要是通过其外特性对系统产生一定影响。电网故障期间，由于其控制系统的快速性，忽略电压跌落、恢复时刻无功功率的变化，可认为电网在故障期间依旧保持功率因数恒定为1。因此，双馈风电机组的外特性等效为一个变化的负电阻。

由于定、转子电抗Ls，Lr与励磁电抗Lm数值相差不大，且转子电流指令值通常为一个较小的数值，因此可忽略转子磁链中转子电流指令值项，不考虑定子磁链暂态过程可得

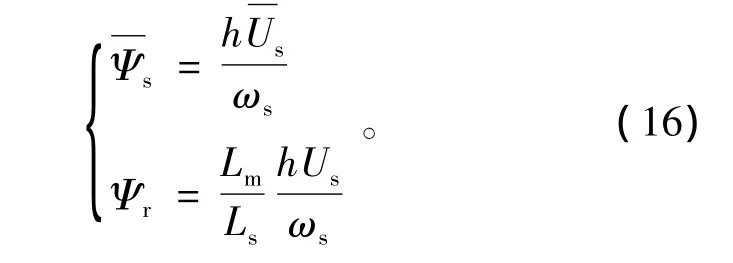
则DFIG暂态过程中的等效电阻

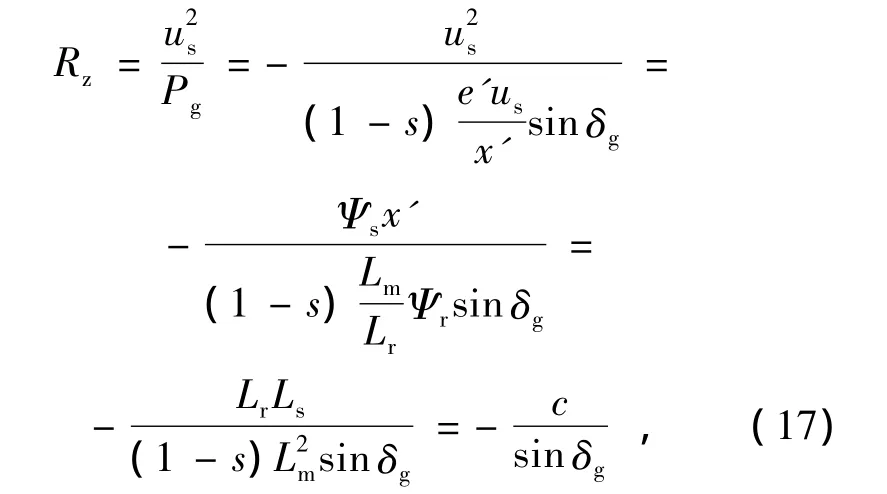
式中:c为常数;e'为暂态值。

由上式可知，双馈风电机组的等效负电阻的大小与其功角的大小有直接关系。由式(2)中的定、转子磁链方程可知，定子磁链空间矢量与转子磁链空间矢量都取决于定子、转子之间的电流量，由于定、转子电感以及励磁电感在数值上极为接近，因此定、转子空间矢量之间的角度差在暂态过程中相差并不大，即暂态过程中DFIG的功角的数值变化在一定范围内，通常为0～90°。可知，随着功角的逐渐变大，其绝对值逐渐变小。

含DFIG的单机输电系统如图2所示。

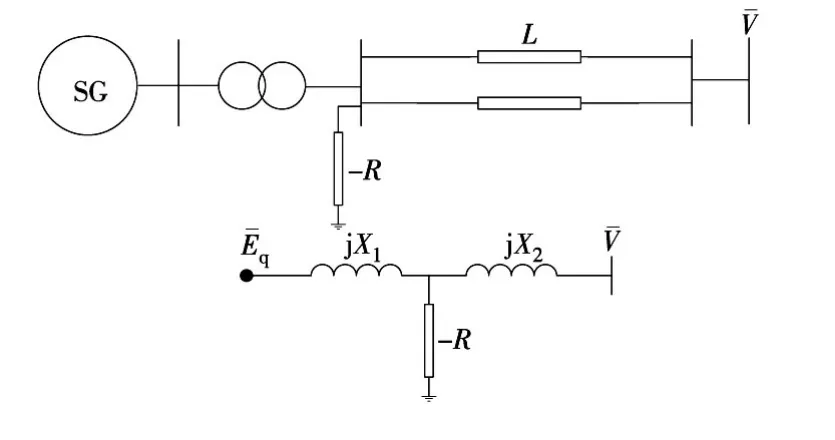
图2 含DFIG的单机输电系统

系统送、受端自阻抗Z11，Z22分别为

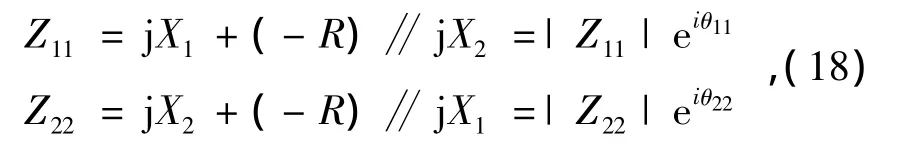
式中:θ11，θ12均大于 π/2 且小于 π，因此有

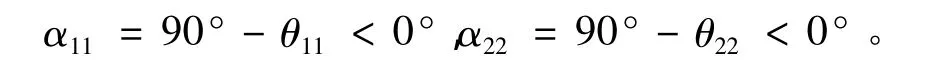
互阻抗Z12为

因为 θ12小于 π/2，所以 α12=90°－ θ12＞ 0°。

则同步发电机电磁功率PEq及无穷大电网提供的电磁功率PV为

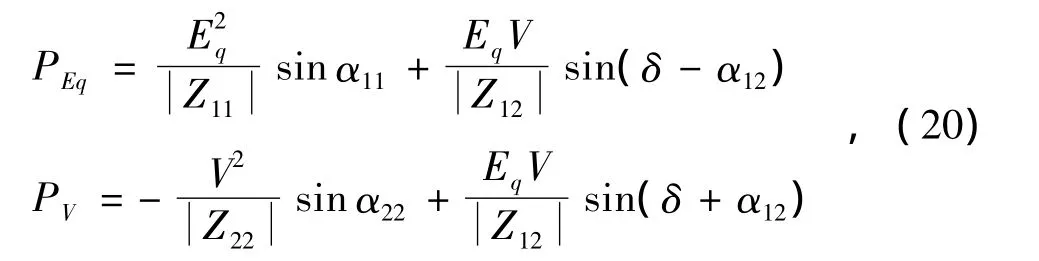
式中:Eq为同步发电机等效内电势;V为无穷大母线电压。

功率曲线如图3所示。

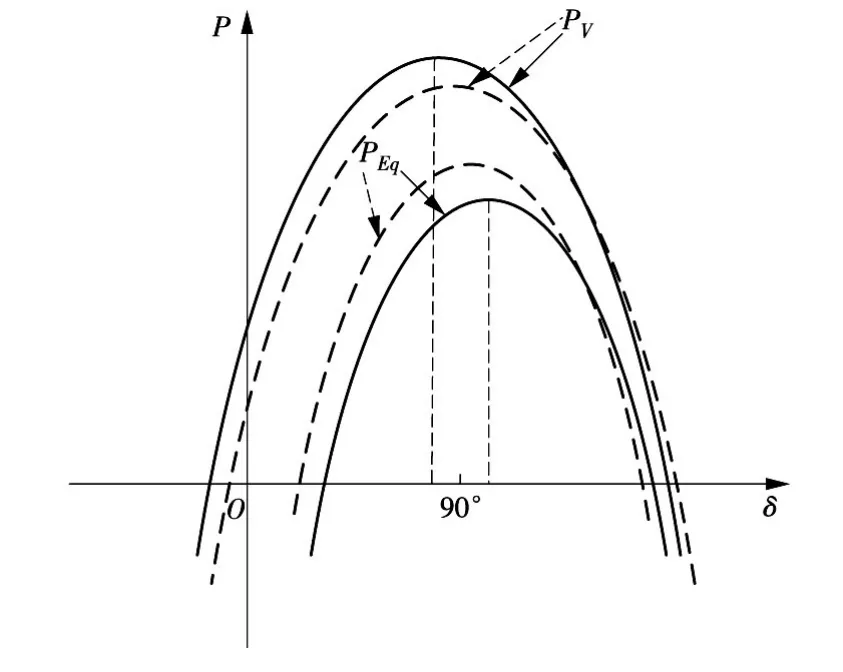
图3 含DFIG的SG功率特性曲线

可证明暂态过程中，随着DFIG的功角摆开，其等效负电阻模值减小时，同步发电机的功率特性曲线向上、向左移动，如图3中的虚线所示，DFIG接入后不仅增加了同步发电机的功率极限，而且功率极限角也随之减小(＞90°)，即在暂态过程中随着功角摆开，电磁功率较DFIG接入前能够快速增加，减少了同步发电机暂态期间的加速能量，有利于其功角稳定。

2.2 常规机组减出力运行条件下的功角稳定特性

DFIG接入常规机组减出力运行时，系统可以用图4来等效分析。风电机组出力替代了部分火电出力，使火电出力减少。

火电机组有功出力PG计算如下

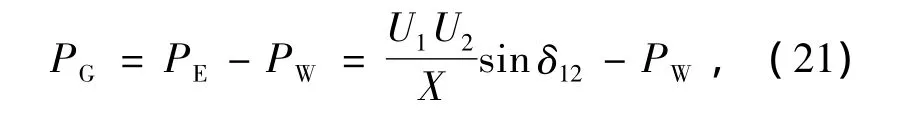
式中:PG为同步发电机组出力;PE为线路传输有功功率;PW为风电机组所分摊的同步发电机出力，即同步发电机组减少的出力。

风电机组并网前后同步电机功率特性曲线不变，等面积分析如图5、图6所示。

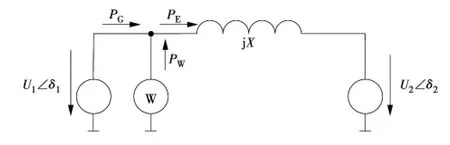
图4 DFIG接入SG减出力示意

图5 不含DFIG的SG功率特性曲线

图6 DFIG接入下的SG功率特性曲线

从图5、图6可以看出，DFIG并网后分摊了系统部分有功出力，各同步发电机组的出力减小，因而机械功率随着减小，在功率特性曲线不变的情况下，当电力系统发生故障时，各同步发电机不平衡加速功率小于风机并网前，而故障恢复后减速功率大于风机并网前，导致系统加速面积减小，减速面积增加，系统稳定裕度提高，因而系统中各同步发电机组的功角能够迅速恢复稳定状态，系统功角稳定特性得到改善。

3 算例分析

本文采用IEEE30节点的标准算例，其相关参数见文献［19］，系统如图7所示。该系统共有30个节点，其中共有6个发电单机节点。其中发电机组1作为整个系统的平衡机组，发电机组2，5，8的额定容量均为60 MW，发电机11额定容量为17.93 MW，发电机13的额定容量为16.91 MW，额定工况下系统总负荷为283.4 MW。母线10在0.2 s时发生三相短路故障，故障持续时间为0.1 s。现仅选取发电机2，5，8的功角曲线进行分析。

母线2处同步发电机组等容量替换为DFIG时，系统中同步发电机组功角曲线如图8所示;母线5处同步发电机组等容量替换为DFIG时，系统中同步发电机组功角曲线如图9所示。

图7 IEEE 30节点系统

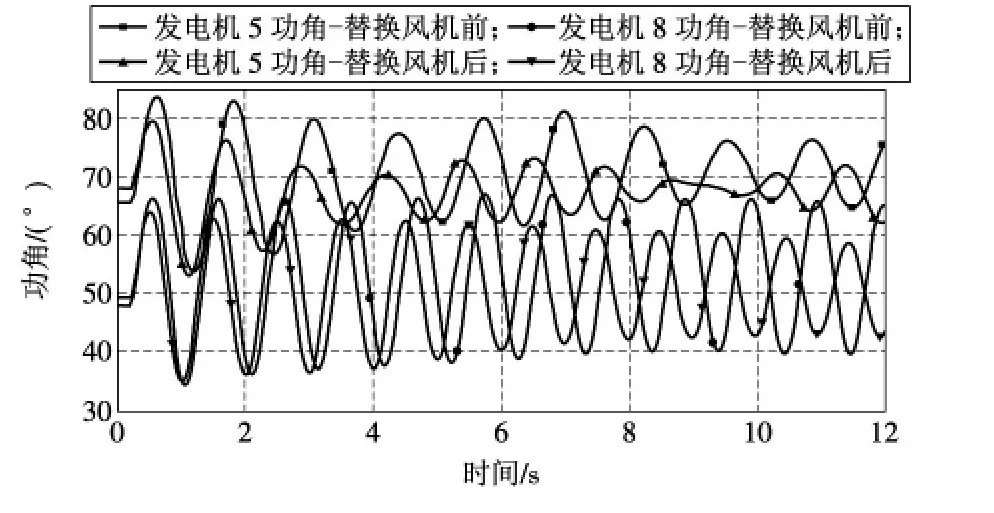
图8 2处等容量替代后的功角曲线

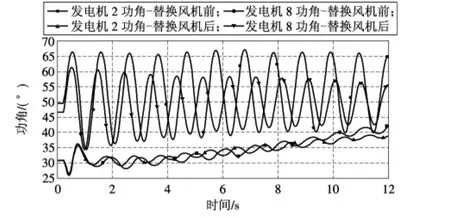
图9 5处等容量替代后的功角曲线

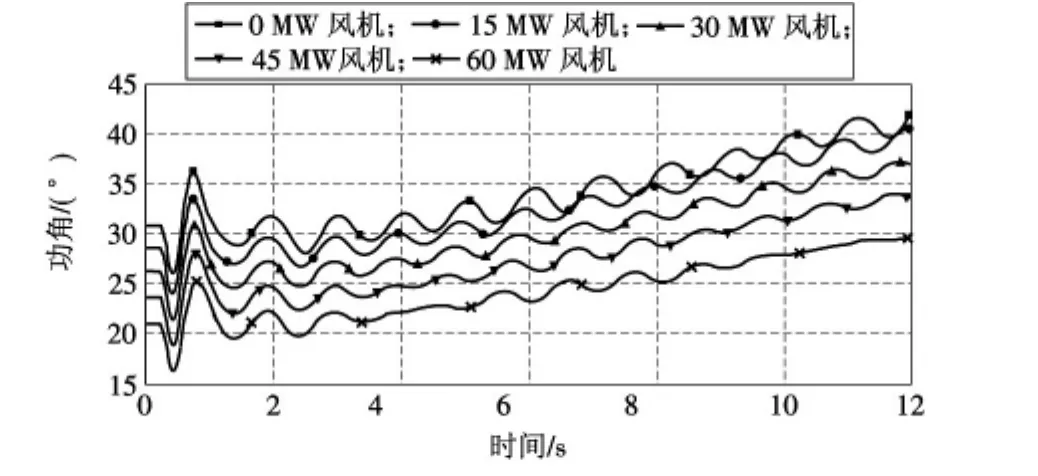
图10 不同DFIG穿透功率下#2发电机功角曲线

从图8～9可以看出DFIG等容量替换同步发电机组接入电网后，各同步发电机组功角稳定特性有一定程度的改善，证明了本文理论分析的准确性。

图10～12为系统中各同步发电机组减出力运行条件下，分别将15 MW，30 MW，45 MW，60 MW双馈风电机组接入母线7后系统中各同步发电机组功角曲线。

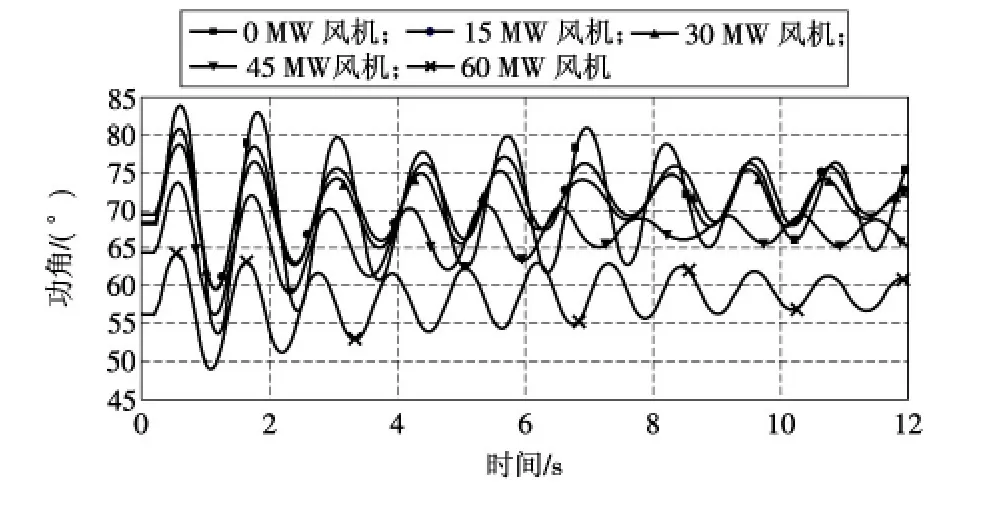
图11 不同DFIG穿透功率下#5发电机功角曲线

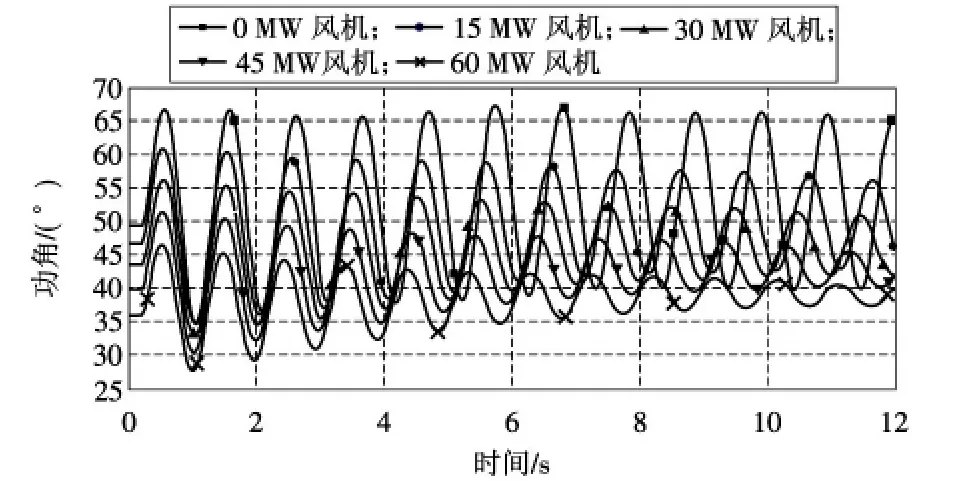
图12 不同DFIG穿透功率下#8发电机功角曲线

由于DFIG并网后承担了部分有功出力，导致各同步发电机组初始机械功率减小，初始功角减小，系统故障后加速面积减少，减速面积增加，各同步发电机组能够更快恢复稳定，从图10～12可以看出，风机并网后各同步发电机组的功角曲线较并网前稳定特性要好，验证了本文理论分析的正确性。

随着风电机组并网容量的不断增加，各同步发电机组初始功率不断减小，初始功角也不断减小，系统中同步发电机组越能快速趋于稳定，使本文的理论分析进一步得验证。

4 结论

本文对双馈发电机的原理和特性进行了分析，在同步发电机组减出力以及等容量替换2种情况下对DFIG接入后同步发电机组的功角稳定特性进行了理论分析和仿真验证，仿真结果表明，2种情况下DFIG接入电网后能够改善系统中各同步发电机组功角稳定特性，且随着风电机组并网容量的不断增大，系统功角稳定性也增加，证明了本文理论分析和推导过程的正确性。

［1］XU L，WEI C.Torque and reactive power control of a doubly fed induction machine by position sensorless scheme［J］.Industrial application，1995，31(3):636-642.

［2］PENA R，CLARE J C，ASHER G.M.Doubly-fed induction generator using back-to-back PWM converters and its application to variable-speed wind-energy generation［J］.Electric power applications，1996，143(3):231-241.

［3］弗拉基斯拉夫·阿赫玛托夫.风力发电用感应发电机［M］.中国电力科学研究院，译.北京:中国电力出版社，2009:24-25.

［4］林莉，孙才新，王永平，等.大容量风电场接入后电网电压稳定性的计算分析与控制策略［J］.电网技术，2008，32(3):41-48.

［5］丁明，李宾宾，韩平平.双馈风电机组运行方式对系统电压稳定性的影响［J］.电网技术，2010，34(10):26-31.

［6］迟永宁，王伟胜，戴慧珠.改善基于双馈感应发电机的并网风电场暂态电压稳定性的研究［J］.中国电机工程学报，2007，27(25):25-31.

［7］贾宏杰，王磊.含大规模风电场的电力系统小扰动稳定性研究［J］.电网技术，2012，36(10):61-69.

［8］李媛媛，邱跃丰，马世英，等.风电机组接入对系统小干扰稳定性的影响［J］.电网技术，2012，36(8):50-55.

［9］曹娜，李岩春，赵海翔，等.不同风电机组对电网暂态稳定性的影响［J］.电网技术，2007，31(9):53-59.

［10］郝正航，余贻鑫.双馈风力发电机组对电力系统稳定性影响［J］.电力保护与控制，2011，39(3):7-11.

［11］TSOURAKIS G，BASIL M Nomikos，CCOSTAS D.Contribution of doubly fed wind generators to oscillation damping［J］.Energy conversion，2009，24(3):783-791.

［12］HUGHES F M，ANAYA L O，JENKINS N，et al.Control of DFIG-based wind generation for power network support［J］.Power systems，2005，20(4):1958-1966.

［13］GAUTAM D，VITTAL V，HARBOUR T.Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems［J］.Power systems，2009，24(3):1426-1434.

［14］VITTAL E，MALLEY M，KEANE A.Rotor angle stability with high penetrations of wind generation［J］.Power systems，2012，27(1):353-362.

［15］MULJADI E，BUTTERFIELD C P，PARSONS B，et al.Effect of variable speed wind turbine generator on stability of a weak grid ［J］.Energy conversation，2007，22(1):29-36.

［16］陈树勇，陈会员，唐晓俊，等.风火打捆外送系统暂态稳定切机控制［J］.电网技术，2013，37(2):514-519.

［17］汤蕴缪.电机学［M］.北京:清华大学出版社，2002:179-193.

［18］欧阳金鑫，熊小欣，张涵轶.电网短路时并网双馈风电机组的特性研究［J］.中国电机工程学报，2011，31(22):17-25.

［19］李娟娟.电网电压骤降的分析评估及其抑制措施［D］.福州:福州大学，2006.