Dynamic modeling and simulation for the flexible spacecraft with dynamic stiffening
2015-04-22LICuichun李崔春MENGXiuyun孟秀云LIUZaozhen刘藻珍
LI Cui-chun(李崔春), MENG Xiu-yun(孟秀云), LIU Zao-zhen(刘藻珍)
(Key Laboratory of Dynamic and Control of Flight Vehicle, Ministry of Education,Beijing Institute of Technology, Beijing 100081, China)
Dynamic modeling and simulation for the flexible spacecraft with dynamic stiffening
LI Cui-chun(李崔春), MENG Xiu-yun(孟秀云), LIU Zao-zhen(刘藻珍)
(Key Laboratory of Dynamic and Control of Flight Vehicle, Ministry of Education,Beijing Institute of Technology, Beijing 100081, China)
A rigid flexible coupling physical model which can represent a flexible spacecraft is investigated in this paper. By applying the mechanics theory in a non-inertial coordinate system, the rigid flexible coupling dynamic model with dynamic stiffening is established via the subsystem modeling framework. It is clearly elucidated for the first time that, dynamic stiffening is produced by the coupling effect of the centrifugal inertial load distributed on the beam and the transverse vibration deformation of the beam. The modeling approach in this paper successfully avoids problems which are caused by other popular modeling methods nowadays: the derivation process is too complex by using only one dynamic principle; a clearly theoretical explanation for dynamic stiffening can’t be provided. First, the continuous dynamic models of the flexible beam and the central rigid body are established via structural dynamics and angular momentum theory respectively. Then, based on the conclusions of orthogonalization about the normal constrained modes, the finite dimensional dynamic model suitable for controller design is obtained. The numerical simulation validations show that: dynamic stiffening is successfully incorporated into the dynamic characteristics of the first-order model established in this paper, which can indicate the dynamic responses of the rigid flexible coupling system with large overall motion accurately, and has a clear modeling mechanism, concise expressions and a good convergence.
non-inertial coordinate system; large overall motion; rigid flexible coupling; dynamic stiffening; normal constrained mode
In early times, a rigid model could be fairly accurate to describe the dynamic characteristics of a spacecraft. With the development of aerospace technology, the number of spacecraft with a variety of flexible appendages such as large area solar panel and large scale flexible antenna is increasing rapidly. While the system is undergoing a large overall motion, the coupling effect of the large overall motion and the elastic deformation of flexible appendage appears. Previous studies of the rigid flexible coupling system were based on the traditional zero-order approximate dynamic model[1-2], which ignored the coupling terms of the large overall motion and the elastic deformation. However, when the system is undergoing large overall motions, especially a motion of high velocity, it would provide a result of unlimited increasing of the deformation of flexible appendages, which is in contradiction with the reality. To solve this problem, based on the study of a cantilever beam attached to a moving platform, Kane put forward the concept of dynamic stiffening for the first time in 1987[3], and pointed out that the large rotation motion would increase the stiffness of the beam. From then on, many scholars started to pay a lot of attentions[4-8]. It becomes an engineering significance whether the dynamic stiffening is incorporated into the dynamic behavior of model established[9-14].
To sum up, there are two key points lying in the dynamic modeling of the rigid flexible coupling system: ① the model established should contain the coupling of the rigid motion and the flexible deformation; ② the dynamic stiffening should be included in the dynamic characteristics of the model. The ideas in most previous papers are to regard the whole system as the research object, and the models are established by employing only one dynamic principle. There are mainly two drawbacks in these papers: ① the coupling degree of the dynamic equations established is too high, and the modeling process is too complex to be conducive for the numerical integration; ② the dynamic stiffening term is captured by truncating the high-order terms of the expansion of the flexible deformation filed, so a really rational explanation for dynamic stiffening is not provided. To solve problems referred, a rigid flexible coupling dynamic model (Hub-Beam) is studied in this paper by adopting the subsystem modeling technique. Firstly, the system is divided into two subsystems: a central rigid body (Hub) and a flexible beam (Beam). The continuous dynamic models are derived via structural dynamics and angular momentum theory respectively. Then, based on the conclusion of orthogonalization about the normal constrained modes of the flexible beam, a space state model is obtained. The numerical simulation shows that, the first-order model in this paper has considered dynamic stiffening, and can indicate the dynamic behavior of the flexible spacecraft with large overall motions accurately. It has a clear modeling mechanism, concise expressions and a good convergence.
The main contribution of this paper is the introduction of the mechanics theory in the non-inertial coordinate system, which considers the dynamic stiffening as a mechanics phenomenon in a non-inertial system. As a result, a clearly theoretical explanation for dynamic stiffening is provided: it is produced by the coupling effect of the centrifugal inertial load distributed on the flexible beam with large overall motions and the transverse vibration deformation of the beam.
1 Continuous dynamic modeling based on mechanics problems in non-inertial system
1.1 Rigid flexible coupling physical model
The rigid flexible coupling physical model (Hub-Beam) is shown in Fig.1. This model can represent a large class of spacecrafts, such as a satellite with solar panel, etc. The effect of orbit maneuver on attitude motion is ignored here. The system shown in Fig.1 consists of a central rigid body (Hub) and a cantilever flexible beam (Beam) attached to Hub. The flexible beam is assumed to be a uniform Euler-Bernoulli beam with the assumption of small deformation and small strain, and the material is assumed to be homogeneous and isotropic.

Fig.1 Rigid flexible coupling physical model (Hub-Beam)
The inertial coordinate systemOIXIYIis built with the center of the central rigid body as the origin. The floating coordinate systemOXYis built on the flexible beam. The deflection curvey=y(x,t) describes the transverse vibration deformation of Beam. The angular rotation of Hub isθ(t). The rigid flexible coupling system shown in Fig.1 is divided into two subsystems. Subsystem 1 is Beam.lis the length,ρbis the mass per unit length,Eis the Young’s modulus of elasticity, andIis the rotary inertia of cross section. Subsystem 2 is Hub.Jstaris the rotary inertia about an axis of rotationOI,bis the radius, andThis the applied torque.
1.2 Modeling of Beam based on structural dynamics
The deformation field of Beam with large overall motions is shown in Fig.2. As a result of the motion of Hub,OXYbecomes a non-inertial coordinate system. Therefore, the research purpose on the dynamic characteristics of the transverse vibration of Beam is to solve a typical mechanics problem in a non-inertia coordinate system. According to structural dynamics, the transverse vibration of Beam is determined by the external distributed load which is perpendicular to the Beam. The corresponding equation is in the form of
(1)
whereq(x,t) is the external vertical distributed load. Therefore, the key to establish the dynamic equation of the transverse vibration of Beam is to obtain the expression of the external vertical distributed load acting on Beam.
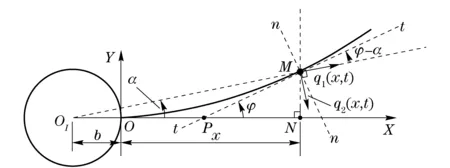
Fig.2 Deformation field of Beam with large overall motion
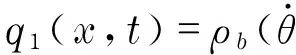
(2)
BasedonthegeometricrelationsshowninFig.2andtheassumptionaboutalittledisplacementandalittleangle,andmeanwhile,thesecond-orderofseriesoftrigonometricfunctionsareomitted,thesimplifiedformoftheexternalverticaldistributedloadactingonBeamcanbewrittenas
(3)
SubstitutingEq. (3)intoEq. (1),thecontinuousdynamicequationofBeamwithlargeoverallmotionsisobtainedintheformof
(4)
1.3 Modeling of Hub based on angular momentum theory
The applied forces related to the attitude motion of Hub are shown in Fig.3.Th(t) is the applied torque.Fs(0,t) andM(0,t) are the force and the torque of Beam acting on Hub at the joint respectively.

Fig.3 Forces and torques acting on Hub

(5)
Thus,thedistributionfunctionsoftheshearforceandthebendingmomentare
(6)
(7)
BasedonEqs. (5)-(7),thecontinuousdynamicequationofHubisintheformof
(8)

2 Discrete dynamic modeling based on the conclusions of orthogonalization about normal constrained modes
The expansion about the firstN-orders of the normal constrained modes is utilized to describe the transverse vibration deformation of Beam approximately as following:
(9)

(10)
(11)
BasedonEqs. (10) (11),thefinitedimensionaldynamicequationofBeamisobtainedasfollowing
(12)
where
q=[q1(t)q2(t)q3(t) …qN(t)]T
(13)
ΛN=diag[ω1ω2ω3…ωN]
(14)
(15)
(16)

Similarly, the finite dimensional dynamic equation of Hub is
(17)
where
(18)
Eqs. (12)-(18) constitute theN-dimensional dynamic model of a flexible spacecraft. With the consideration of dynamic stiffening, the first-order dynamic model is not only suitable for the engineering background of a small angular maneuver, but also meets the requirements of a large angular maneuver in the complex aerospace missions nowadays. According to Eqs. (12)-(18), the state space equations of the system are
(19)
where
(20)

3 Numerical simulation validation
The validations of the rigid flexible coupling dynamic model of a flexible spacecraft are carried out in 2 aspects: ① the validation of dynamic stiffening when the large overall motion is known; ② the validation of the convergence of the first-order model with dynamic stiffening when the large overall motion is unknown.
3.1 Validation of dynamic stiffening
Refer to the system parameters in Ref. [16]: Beam of lengthl=8 m, Young’s modulus of elasticityE=6.895 2×1010N/m2, sectional areaA=7.296 8×10-5m2, bulk densityρ=2.766 7×103kg/m3, rotary inertia of cross sectionI=8.218 9×10-9m4; Hub of radiusb=0.5 m, rotary inertiaJstar=300 kg·m2. The regular pattern of the known large overall motion is
(21)
whereωmis the final angular velocity of Hub. The value ofωmequals to 0.5 rad/s, 2 rad/s and 4 rad/s respectively in the simulation. Fig.4 is the response of the tip transverse vibration displacement of Beam with large overall motions defined in Eq. (21). Hereinto, the dotted lines correspond to the responses of ZDM, and the solid lines correspond to the responses of FDM. By analyzing the natural frequencies of Beam, the first-order and the second-order natural frequencies are respectively 2.91 rad/s and 18.24 rad/s.
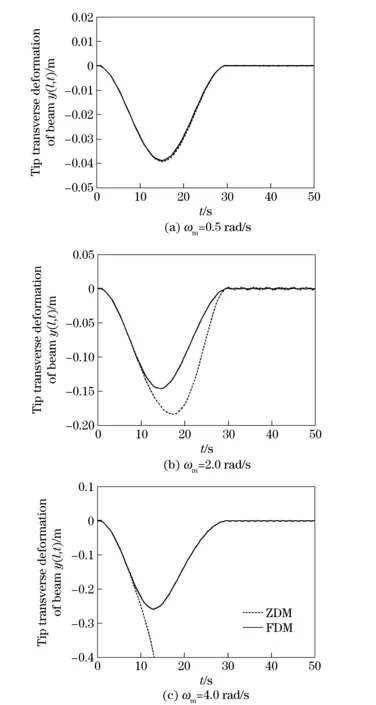
Fig.4 Responses of tip displacement of Beam with known large overall motions
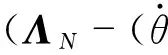
To sum up, with the increasing of the final velocity (ωm), the simulation results of ZDM start to become invalid, until divergent. According to analyses about the dynamic terms in Eq. (12), the dynamic softening effect plays a great role in the dynamic behaviors of system at this moment, so the larger the value ofωmis, the more obvious the softening effect is. It should be noticed that, even though the angular velocity of the motion of Hub is quite large, FDM can still predict the dynamic behaviors of the system with a convergent simulation result. It just corresponds to the analysis conclusion about the positive definitiveness of the stiffness matrix of FDM. Thus, FDM has successfully incorporated dynamic stiffening into the dynamic behavior of the system, and could meet the requirements of practical engineering.
3.2 Validation of the convergence of first-order model
Set the parameters of Beam: lengthl=5 m, sectional areaA=4×10-4m2, rotary inertia of cross sectionI=1.333×10-8m4, bulk densityρ=2.766 7×103kg/m3, Young’s modulus of elasticityE=6.895 2×1010N/m2. Ignore the central rigid body (Hub), that is to sayJstar=0 andb=0. The external torque is

Fig.5 Responses of the first-order model when Thm=50 N·m
(22)
whereTm=2 s, andThmis the maximum of torque, which equals 50 N·m.
Fig.5 corresponds to the simulation results whenThm=50 N·m. The tip maximum response amplitude is 0.42 m, and when the system reaches the steady state, the amplitude of the micro continuous oscillation of Beam is about 0.07 m. It can be seen from Fig.5 that, although the torque is very large, the simulation results are still convergent. It should be pointed out that, in the same simulation condition, the simulation results of the first-order approximate coupling dynamic model presented in general papers are rapidly divergent[19]. Thus, the model established in this paper (FDM) not only has a clear modeling mechanism and concise expressions, but also has a good convergence. Even if the simulation conditions are very harsh, FDM can still indicate the dynamic responses of the system accurately.
4 Conclusions
A rigid flexible coupling physical model is investigated in this paper.To simplify complex modeling process, this paper applys the mechanics theory in a non-inertial coordinate system, then the rigid flexible coupling dynamic model with dynamic stiffening is established via the subsystem modeling technique. According to the modeling process, theoretical analyses and numerical simulation validations, the following conclusions are obtained:
① By applying the subsystem modeling technique, the models are established via structural dynamics and angular momentum theory. The modeling approach in this paper successfully solves problems caused by other popular modeling methods, and the modeling process is simplified here. Meanwhile, it meets the requirement about the coupling of the rigid motion and the flexible deformation in the dynamic behavior of the flexible spacecraft.
② Dynamic stiffening is considered as a typical mechanics phenomenon in a non-inertial system. By introducing the mechanics theory in a non-inertial coordinate system, dynamic stiffening is successfully incorporated into the dynamic behavior of the system. The numerical simulations show that: the established FDM is not only with the consideration of dynamic stiffening under the background of a large angular maneuver of the flexible spacecraft, but also has a good convergence in the simulation under extreme conditions. FDM can indicate the dynamic responses of the system accurately.
③ A clearly theoretical mechanism of dynamic stiffening is provided in this paper: it is produced by the coupling effect of the centrifugal inertial load distributed on the beam and the transverse vibration deformation of the beam. It gives a way out of the dilemma about dealing with dynamic stiffening in previous papers.
[1] Hu Qinglei, Shi Peng, Gao Huijun. Adaptive variable structure and commanding shaped vibration control of flexible spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 804-815.
[2] Shan Jinjun, Liu Hongtao, Sun Dong. Modified input shaping for a rotating single-link flexible manipulator[J]. Journal of Sound and Vibration, 2005, 285(1-2): 187-207.
[3] Kane T R, Ryant R R. Dynamics of a cantilever beam attached t o a moving base[J]. Journal of Guidance, Control and Dynamics, 1987, 10(2): 139-151.
[4] Banerjee A K, Dickens J M. Dynamics of an arbitrary flexible body in large rotation and translation[J]. Journal of Guidance, Control and Dynamics, 1990, 13(2): 221-227.
[5] Zhang D J, Liu C Q, Huston R L. On the dynamics of an arbitrary flexible body with large overall motion: an integrated approach[J]. Mechanics of Structures and Machines, 1995, 23(3): 419-438.
[6] Jiang Lizhong, Hong Jiazhen, Zhao Yueyu. Coupling dynamical modeling theory of elastic beam-in large overall motions[J]. Chinese Journal of Computational Mechanics, 2002, 19(1): 12-15. (in Chinese)
[7] Yang Hui, Hong Jiazhen, Yu Zhengyue. Dynamics modeling and numerical simulation for a rigid-flexible coupling multibody system[J]. Chinese Journal of Computational Mechanics, 2003, 20(4): 402-408. (in Chinese)
[8] Jiang Jianping, Li Dongxu. Research on rigid-flexible coupling dynamics of spacecraft with solar panel[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3): 418-422. (in Chinese)
[9] Yang Zhengxian, Kong Xianren, Liao Jun, et al. Dynamic modeling and simulation for the rigid-flexible coupling system with large overall motion[J]. Spacecraft Environment Engineering, 2011, 28(2): 141-146. (in Chinese)
[10] Liang Lifu, Wang Peng, Song Haiyan. The study of the dynamic stiffening problem in a non-inertial coordinate system[J]. Journal of Harbin Engineering University, 2012, 33(8): 1052-1056.
[11] Bai Shengjian, Huang Xinshen. Building control-oriented simulation environment for flexible spacecraft[J]. Journal of System Simulation, 2010, 22(2): 302-305. (in Chinese)
[12] García-Vallejo D, Sugiyama H, Shabana A A. Finite element analysis of the geometric stiffening effect. Part 1: a correction in the floating frame of reference formulation[J]. Journal of Multi-body Dynamics, 2005, 219(2): 187-202.
[13] Huang Yong’an, Deng Zichen, Yao Linxiao. An improved symplectic precise integration method for analysis of the rotating rigid-flexible coupled system[J]. Journal of Sound and Vibration, 2007, 299(1-2): 229-246.
[14] Chen Sijia. Researches on the rigid-flexible coupling problem and the dynamic modeling theory of multi-link spatial flexible manipulator arms[D]. Nanjing: Nanjing University of Science and Technology, 2012. (in Chinese)
(Edited by Wang Yuxia)
10.15918/j.jbit1004-0579.201524.0304
V 414.33 Document code: A Article ID: 1004- 0579(2015)03- 0305- 08
Received 2013- 11- 26
E-mail: mengxy@bit.edu.cn
杂志排行
Journal of Beijing Institute of Technology的其它文章
- High-rise building fire pre-warning model based on the support vector regression
- Experimental study on the time-dependent dynamic mechanical behaviour of C60 concrete under high-temperatures
- Experimental study on compression stroke characteristics of free-piston engine generator
- Numerical simulation and optimization of the cylinder head water jacket based on the two-phase flow boiling heat transfer
- Multi-action-based approach for constructing knowledge map
- Slow driving control of tracked vehicles with automated mechanical transmission based on fuzzy logic
