Recurrent formula of Bernoulli numbers and the relationships among the coefficients of beam,Bernoulli numbers and Euler numbers

LAO Da-zhong(老大中), ZHAO Shan-shan(赵珊珊), LAO Tian-fu(老天夫)

(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Dandong Design Institute of Chemical Fibre, Dandong, Liaoning 118002, China;2.China National General Machinery Engineering Corporation,Beijing 100050, China)



Recurrent formula of Bernoulli numbers and the relationships among the coefficients of beam,Bernoulli numbers and Euler numbers

LAO Da-zhong(老大中)1, ZHAO Shan-shan(赵珊珊)2, LAO Tian-fu(老天夫)3

(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Dandong Design Institute of Chemical Fibre, Dandong, Liaoning 118002, China;2.China National General Machinery Engineering Corporation,Beijing 100050, China)

Based on the differential equation of the deflection curve for the beam, the equation of the deflection curve for the simple beam is obtained by integral. The equation of the deflection curve for the simple beam carrying the linear load is generalized, and then it is expanded into the corresponding Fourier series. With the obtained summation results of the infinite series, it is found that they are related to Bernoulli numbers andπ.TherecurrentformulaofBernoullinumbersispresented.Therelationshipsamongthecoefficientsofthebeam,BernoullinumbersandEulernumbersarefound,andtherelativemathematicalformulasarepresented.

Bernoulli numbers; Euler numbers; coefficients of beam; simple beam; equation of deflection curve; Fourier series

It is well known that Euler numbers and Bernoulli numbers are the very important because they are used in many mathematical calculations. For example, according to the theory of summation of series[1], there are following formulas

(1)

(2)

(3)

whereB2kis a Bernoulli number,E2kis an Euler number.

Through the Fourier series expansion of the equation of the deflection curve for the simple beam carrying the linear load in the present work, the relationships among the coefficients of beam, Bernoulli numbers and Euler numbers are established, therefore the recurrence formula of Bernoulli numbers is derived, and the above-mentioned summation formulas of series are generalized.

1 Equation of the deflection curve for the simple beam and its generalization

Let a small deflection beam carry the distributed loadq(x),Lis the length of the beam,EIis the flexural rigidity, it is known from the theory of mechanics of material[2]that the differential equation of the deflection curve of the beam is

(EIy″)″-q(x)=0

(4)

whereyis the deflection of the beam.

IfEIis a constant, then Eq. (4) can be written as

EIy(4)=q(x)

(5)

The relationship of the deflection and bending momentMof the beam is

EIy″=-M

(6)

(7)

Theboundaryconditionsare

y(0)=y(L)=0，y″(0)=y″(L)=0

(8)

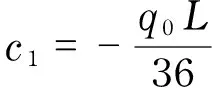
(9)

BecausebothEIandq0are constants, the function can also be constructed like this, Eq. (5) is written as

(10)

IntegratingEq. (10)fourtimes,andmakinguseoftheboundaryconditions(8),weobtain

(11)

(12)

Theboundaryconditionsare

y4m+1(0)=y4m+1(L)=0，y4m-1(0)=y4m-1(L)=0

(13)

where the two left boundary conditions have been satisfied.

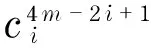
(14)

(15)

It is known from Eq. (14) and Eq. (15) that when the indices ofxare permuted according to descending order of powers, the various coefficients of the beam function appear alternately with the different signs, and the algebraic sum of various coefficients is zero; the times of factorial is just the highest powerful number ofx; the lower order polynomial can be obtained by the derivative of the higher order one.

2 Fourier sine series expansion of the beam function

According to the boundary conditions (8), in the interval [0,L], Eq. (11) can be expanded into the Fourier sine series, its form is

(16)

wherethecoefficientbncan be written as

(17)

SubstitutingEq. (17)intoEq. (16),thensubstitutingEq. (16)intoEq. (11),weobtain

(0≤x≤L)

(18)

(19)

AccordingtoEq. (19),theFouriersineseriesofEq.(12)canbewrittenas

(0≤x≤L)

(20)

IfL=1 is chosen, then there is

(0≤x≤1)

(21)

Applying odd time derivative to the Fourier sine series, the Fourier cosine series can be obtained. No matter whether Fourier sine series or Fourier cosine series, their sum relates toπ,andthepowerexponentofπequalstothepowerexponentofn.

3 Relationships among the coefficients of the beam, Bernoulli numbers and Euler numbers

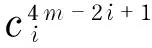
(22)

(23)

InEqs. (22) (23),changing2mintok, then there are

(24)

(25)

(26)

ThesolutionoftheinitialcoefficientCkfrom Eq.(26) is

(27)

Ofcourse,fork=0 Eq.(27) can hold too.

(28)

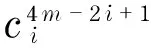
(29)

Changing2mintok, then Eq.(29) can be written as

(30)

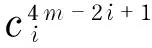
Especially, for the first coefficient of the beam, there is

(31)

Obviously,forthelastcoefficientofthebeam,thereis

(32)

SubstituteingEq.(30)intoEq.(25),andmakeuseofEq.(1),thereis

(33)

ItcanbeobtainedfromEq.(33)

(k=0,1,…,n,…)

(34)

Eq.(34) can be rewritten as

(35)

B2kissolvedfromEq.(34)orEq.(35)

(k≥2)

(36)

For examples

(37)

(38)

(39)

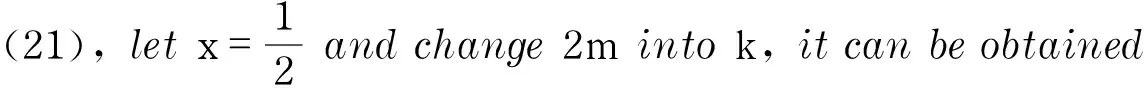
(40)

ItisknownfromEqs.(3) (40)thatEulernumbersandthecoefficientsofthebeamhavethefollowingrelationships

(41)

or

(42)

SubstitutingEq.(30)intoEq.(42),therelationshipsbetweenEulernumbersandBernoullinumbersare

(43)

OfcourseEq.(43)alsoholdsfork=0, in this case,k

It is necessary to point out that there are many formulas of Euler numbers expressed by Bernoulli numbers. Refs.[5-10] also give the similar formulas, it shows that the formulas of Euler numbers expressed by Bernoulli numbers are not unique.

According to calculations of Eqs.(27) (36) (43), 11 Bernoulli numbers, corresponding Euler numbers and coefficients of the beam are given in Tab.1. It can be seen from Tab.1 that the numerators and denominators of the initial coefficients are all odd numbers. Euler numbers and the initial coefficients have the same symbols, but they are contrary to the symbols of Bernoulli numbers. The absolute values of Bernoulli numbers, Euler numbers and the initial numbers are all rapid rising series.

Tab.1 Table of Bernoulli numbers, Euler umbers and initial coefficients

Making use of date provided by Tab.1, the coefficients of the beam can be conveniently calculated by Eq.(30), such as

(44)

(45)

Itcanbeseenthatthetwocoefficientsarerespectivelythecoefficientsofx3andxin Eq.(9). The other examples are

(46)

(47)

Theabove-mentionedresearchresultsshowthattheFourierseriesexpandedbythereflectionequationofthesimplebeamcarryingthelinearload,nomatterwhethertheFouriersineseries,ortheFouriercosineseriesobtainedthroughderivation,thecoefficientsofthebeam,theinitialcoefficientsandEulernumbers,areallrelatedtoBernoullinumbers,theycanallexpressedwithBernoullinumbers,andallBernoullinumberscanbecalculatedbymeansofrecurrenceformula(36).Therearecertainrelationshipsamongthecoefficientsofthebeam,BernoullinumbersandEulernumbers.

4 Applies of the coefficients of the beam in the summation of the series

(48)

(49)

(50)

(51)

(52)

(53)

(54)

InEq.(20),choosingm=2, then deriving Eq.(20), we obtain

(55)

(56)

(57)

(58)

(59)

(60)

(61)

5 Conclusions

①Through the equation of the deflection curve for the simple beam carrying the linear load and the expansion of the generalized Fourier series, the recurrence formula Eq.(36) of Bernoulli numbers has been derived, and it can calculate all Bernoulli numbers. The result is that the bigger numbering Bernoulli number can be expressed by the combination of the smaller numbering Bernoulli numbers.

② The relationships among the coefficients of the beam, Euler numbers and Bernoulli numbers, or the relationship between the coefficients and Bernoulli numbers are expressed by Eq.(29) or Eq.(30), the relationship between Euler numbers and the coefficients of the beam is Eq.(41) or Eq.(42), The relationship between Euler numbers and Bernoulli numbers is Eq.(43). The relationship between Euler numbers and Bernoulli numbers has many expressions.

③ The summation of alternating series composed by the reciprocals of the odd powers of the natural numbers can be obtained by the beam function of the simple beam carrying the linear load being expanded into Fourier sine series. The summation of alternating series composed by the reciprocals of the even powers of the natural numbers can be obtained by the derivatives of the above Fourier sine series.They are all the concrete expressional forms of the beam function (12) being expanded into a Fourier series.

④ The Fourier series expanded by the reflection equation of the simple beam carrying the linear load, no matter whether the Fourier sine series, or the Fourier cosine series obtained through derivation, are all related to Bernoulli numbers, they can all expressed with Bernoulli numbers.

⑤ The summation results of all the above-mentioned series relate to π, and the power exponent of π equals the power exponent ofn.

[1]NeitzH.Mathematicalformulas[M].ShiShengwen,transl.Beijing:OceanPress, 1983. (inChinese)

[2]StephenPTimoshenko,JamesMGere.Mechanicsofmaterials[M].NewYork:VanNostrandReinholdCompany, 1972.

[3]ZhuWeiyi.TworeausiveformulaofcalculatingBernoulli’snumbers[J].JournalofShangqiuTeachersCollege, 2003, 19(2):43-45.(inChinese)

[4]GuJiangmin,ZhuWeiyi.TwokindsofnewexpressionsofBernoullinumbers[J].JournalofWeinanTeachersUniversity, 2010, 25(2):6-8. (inChinese)

[5]ChenZhiming.SomeidentitiesEulernumbersandBernoullinumbers[J].PureandAppliedMathematics, 1994, 10(1): 7-10.(inChinese)

[6]WangDuanzhong.TherelationbetweenEulernumberandBernoullinumberandtheirapplication[J].JournalofNingxiaInstituteofTechnology, 1997, 9(4): 18-20. (inChinese)

[7]LuoQiuming,GuoTianfen,QiFeng.RelationsofBernoullinumbersandEulernumbers[J].JournalofHenanNormalUniversity,2003, 31(2): 9-11. (inChinese)

[8]ZhangSheng.SomeidentitiesrelatedtoEulernumbers[J].JournalofInnerMongoliaNormalUniversity, 2006, 35(1): 44-46. (inChinese)

[9]LaoDazhong,ZhaoBaoting.Fourierseriesbasedonthedeflectionequationexpansionofthesimplebeam[J].TransactionsofBeijinginstituteoftechnology, 2010, 30(1): 1-4. (inChinese)

[10] Wang Chenying, Zong Zhaoyu. Some identities involving Bernoulli and Euler numbers[J]. Journal of Nanjing University of Information Science and Technology: Natural Science Edition, 2012, 4(3): 285-288. (in Chinese)

(Edited by Wang Yuxia)

10.15918/j.jbit1004-0579.201524.0303

O 156.4; O 174.21 Document code: A Article ID: 1004- 0579(2015)03- 0298- 07

Received 2014- 01- 08

Supported by the National Natural Science Foundation of China (51276017)

E-mail: laodazhong@tsinghua.org.cn