基于温度及芯模变形作用的复合材料缠绕张力设计

张 军，史耀耀，康 超，张晓扬

(西北工业大学 现代集成制造技术教育部重点实验室， 西安 710072)



基于温度及芯模变形作用的复合材料缠绕张力设计

张 军，史耀耀，康 超，张晓扬

(西北工业大学 现代集成制造技术教育部重点实验室， 西安 710072)

基于复合材料缠绕成型过程对工艺参数的要求，针对缠绕过程中芯模变形和加热温度对缠绕层应力分布影响等问题，建立温度和芯模变形作用下的缠绕张力设计数学模型。研究了温度引起缠绕层的应力分布解析模型，分析了缠绕内层和芯模在外层压力影响下制品的应力分布，结合3种典型的张力缠绕模型，研究了芯模内外径比以及张力锥度系数对缠绕层剩余张力的影响。提出实现缠绕制品等剩余张力下，初始缠绕张力和温度的理论关系。计算解析解与现有文献一致，文章考虑芯模变形和温度对制品应力影响，计算方法更符合实际，研究结果可用于缠绕张力设计和固化应力分析。

剩余张力;芯模变形;热应力;张力分布

0 引言

复合材料因其具有比强度、比模量高、热稳定性好和重量轻等优点[1-2]，已被广泛应用于载人航天、探月计划、四代机及风力发电等装备的主要结构部件上。然而复合材料结构件的性能不仅取决于材料自身性能，更重要的是取决于成型工艺方法和工艺参数[3]。在复合材料缠绕成型过程中，张力和温度是2个关键的工艺参数，张力是指对预浸布带施加一定的拉力，一方面可使布带拉直，从而使其均匀地承受载荷，另一方面，能使布带层间加压粘接，驱除气泡，提高缠绕制品的致密度，同时也有利于树脂渗透。温度是指在布带缠绕到芯模过程中对布带进行加热，使其中的树脂具有一定的流动性。缠绕过程中，恒张力缠绕会导致布带和纤维褶皱和厚度不均[4]，这是由于外缠绕层张力对内层产生了放松效应，同时布带缠绕过程中受热产生变形。因此，需要分析研究初始缠绕张力和加热温度与剩余张力之间的关系，如何设计初始缠绕张力和加热温度，实现缠绕制品等应力分布[5]，是解决问题的关键。目前，针对缠绕张力和温度的诸多研究，主要围绕缠绕过程传热分析和张力稳定的算法控制以及缠绕张力与制品残余应力理论研究等。

Lu Haibo[6]提出一种研究热塑性纤维缠绕剩余应力的方法，通过调整布带张力，使剩余应力在合理范围。Bakaiyan H[7]在三维各项异性弹性力学基础上，研究了复合材料管在内压力和温度梯度作用下热应力和变形，提出一种精确求解方法。吴德会等[8]利用弹性叠加原理建立了计算缠绕张力导致复合材料管残余内应力变化的模型和方法，提出了一种基于神经网络的纤维缠绕厚壁复合材料管的张力优化设计方法。文琼华[9]提出一种基于热弹性理论计算预浸料形变的方法，通过实验验证了自动铺放过程中温度对预浸料粘附性和带宽变形均有影响。段玉岗[10]通过正交试验与单因素实验结合，研究了复合材料铺放过程中压紧力、预浸带加热温度及芯模温度对复合材料力学性能的影响，结果表明压紧力和加热温度对层间剪切强度影响很大，加热温度对纤维和树脂的分布均匀性也有很大影响。刘成旭[11]研究了环向缠绕层在缠绕过程中的剩余张力变化规律，提出了考虑芯模变形影响的剩余张力分析方法和缠绕张力设计方法。然而，这些研究学者在研究等应力缠绕的同时，并未考虑因缠绕温度对布带和纤维引起的热应力，单纯从张力设计的角度进行等应力缠绕分析很可能导致结果偏差较大。

本文考虑芯模弹性变形和缠绕温度引起的热应力，依据弹性力学和热力学理论，提出基于温度作用的缠绕等应力分析方法和张力设计方法。基于叠加原理和傅里叶传热定律，建立外层剩余张力对内层应力影响模型和缠绕层温度场，通过对给定张力和温度确定缠绕剩余张力和指定剩余张力对缠绕张力和温度进行设计两类问题的研究，讨论了影响缠绕层剩余张力的主要因素。

1 缠绕层温度场分析和热应力

缠绕加热模型如图1所示，包含了芯模和压辊2部分，因为在缠绕过程中布带主要与这2部分发生热传递现象。如图1所示加热模型，将坐标原点放在芯模中心，C点处为布带进给方向，从A点开始对布带进行加热，包括热风的预热和热辊的加热，在缠绕过程中，压辊对布带和芯模施加一定的压力，使布带与芯模及内层布带紧密贴合，保证热传递的效率。

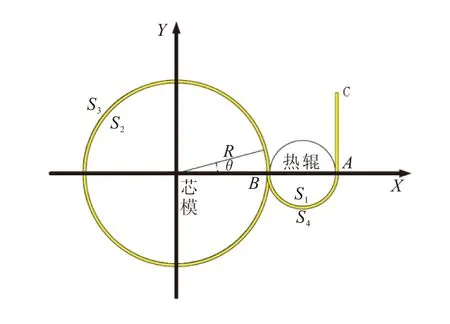
图1 缠绕加热模型Fig.1 Heating model of winding process

1.1 导热方程及传热模型

复合材料缠绕中主要使用纤维和布带为原料，压辊加热面积远大于布带和纤维宽度值，因此热传递现象主要发生在预浸带厚度方向，沿预浸带长度和宽度方向发生的热传递可忽略不计。可得到导热微分方程：

式中T为温度关于空间坐标系Z和时间t的函数。

纤维和布带经过热风预加热和热辊的加热之后，温度为T，缠绕制品可看做是筒体，柱坐标形式下稳态传热方程为

(1)

式中r为半径；T(r)为径向温度分布函数。

多层结构在半径方向满足热流连续条件：

(2)

式中λ、R、T分别表示导热系数、界面半径和界面温度；下标n表示第n层。

当n=1时，表示内衬层，与芯模接触，其导热系数为常数；当n=2,3,4,…时，表示布带缠绕层。这里只考虑其在径向主方向的传热，各层边界条件如图2所示。

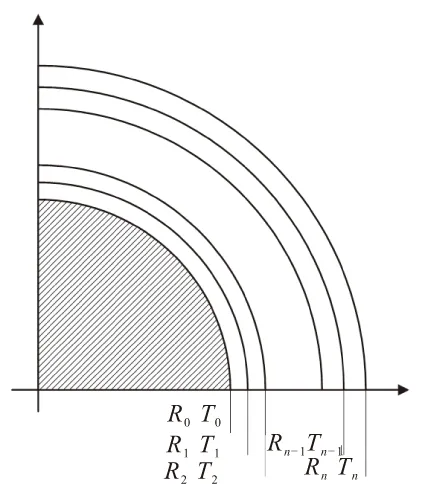
图2 缠绕层温度边界条件Fig.2 Boundary conditions of temperature in winding layerss

1.2 温度场及应力分布

根据缠绕层温度边界条件联立式(1)和式(2)，可得布带缠绕过程中的温度场计算模型：

(3)

布带缠绕连续进行，每层布带的最终温度即布带缠绕制品温度场可由式(3)得到，由《复合材料手册》可查得环氧树脂炭纤维复合材料性能参数如表1所示。

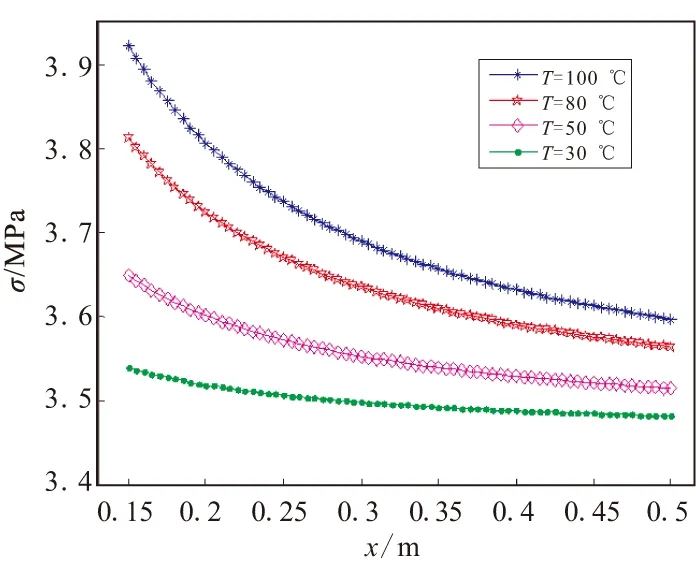
图3 缠绕层热应力分布图Fig.3 Thermal stress distribution of winding layers

表1 环氧树脂炭纤维复合材料性能参数Table 1 Performance parameters of epoxy resin carbon fiber composite materical

2 缠绕层变形和应力

2.1 缠绕层几何与物理方程

缠绕模型如图4所示，a、b分别为芯模内、外壁半径。下标“r”和“θ”分别表示沿径向和环向的物理量。FW(rj)为缠绕层第j层的缠绕剩余张力，rj为该层半径，P为FW(rj)产生的对内层压力。E、ν分别为材料的弹性模量和泊松比。

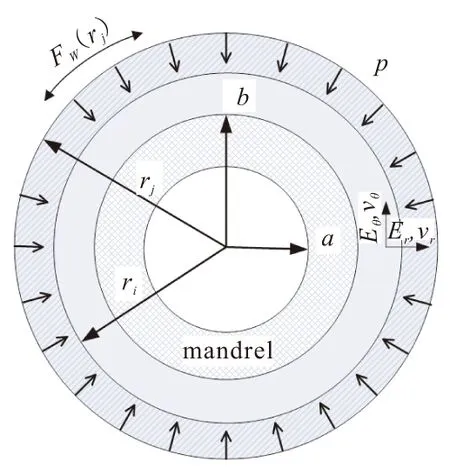
图4 缠绕层横截面Fig.4 Cross section of the winding layers

对于缠绕层，在小变形情况下，其位移μ和应力ε满足以下几何关系：

(4)

同时，芯模和缠绕层的应力应变关系可表示为

(5)

由式(4)和式(5)可得

(6)

(7)

2.2 缠绕层平衡方程

筒形纤维缠绕层满足平衡方程:

(8)

将式(6)、式(7)代入平衡方程式(8)得

ur=c1rβ+c2r-β

(9)

将位移通解式(9)分别代入式(7)和式(8)得

σr=c1S1rβ-1-c2S2r-β-1

(10)

σθ=c1S3rβ-1+c2S4r-β-1

(11)

其中，

2.3 缠绕层边界条件及应力

(12)

将边界条件带入可解出c1和c2：

(13)

其中，H1=Kb-S1，H2=Kb+S2。进一步求解出σr和σθ：

(14)

(15)

3 缠绕层剩余张力分析

缠绕层的应力和应变不仅与缠绕层和芯模材料有关，还与缠绕过程中布带温度有关。同时，随着缠绕层数增加，外层缠绕张力引起外压增大，使内层剩余张力不断减小，定义纤维或布带以初始张力FW(r)缠绕到芯模上，由于受到外缠绕层引起的张力放松ΔF1，以及受热变形引起的热应力ΔF2，使得缠绕层的剩余张力F(r)要考虑缠绕层的几何尺寸以及纤维或布带的温度场。根据弹性叠加原理可得：

F(r)=FW(r)+ΔF1+ΔF2

(16)

缠绕n层后，作用在第i层上总的环向内应力σθ(r)为初始缠绕张力FW(r)、外层对其应力影响以及温度产生热应力之和。依次建立剩余张力公式：

+Eα(T(r)-T(0))

Eα(T(r)-T(0))

(17)

将缠绕层温度场和式(17)代入得：

(k=1,2,…,n)

(18)

考虑到缠绕层厚度h较小，使用积分代替累加：

(19)

F(x)=FW(x)+h(H1S4-H2S3(x)2β)(x)-β-1

(20)

3.1 恒张力模型下剩余张力分析

设恒张力FW(x)=f，对式(20)进行化简可得

(21)

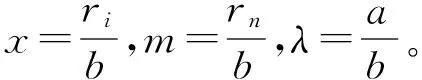
由式(21)可得恒张力下剩余张力分布如图5所示：剩余张力随芯模内、外径比λ的增大而减小；同时随外层布带加热温度的升高而减小。

3.2 恒力矩模型下剩余张力分析

(22)

(a)T=50 ℃

(b)T=100 ℃

由式(22)可得恒力矩下剩余张力分布图(见图6)。图6中剩余张力随芯模内、外径比λ增大而减小；同时随外层布带加热温度的升高而减小。在[1,1.2]区间，剩余张力随缠绕层半径增大而递增。

3.3 锥度张力模型下剩余张力分析

(1)设线性锥度FW(x)=f(1-kx)(k为锥度系数)，对式(20)进行化简可得

(23)

其中

由式(23)可得到线性锥度张力作用下，缠绕层剩余张力分布，如图7所示为线性锥度系数k=0.3时缠绕剩余张力随缠绕半径变化。从图7可看出，缠绕剩余张力随芯模内、外径比λ增大而减小，在[1,1.2]区间，剩余张力随缠绕层半径增大而递增。

(a)T=50 ℃

(b)T=100 ℃

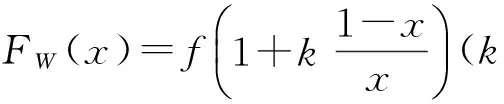
(24)

由式(24)可得双曲锥度k=0.3时剩余张力分布图(图9)。从图9可看出,剩余张力随芯模内、外径比λ增大而减小；在[1,1.2]区间，剩余张力分布随缠绕层径向厚度增大而递增。图10为芯模内、外径比λ=0.3时，不同锥度系数k下剩余张力分布，从图中可看出，缠绕层径向比在1值附近时，剩余张力随锥度系数k增大而递减；在1.2值附近，剩余张力随锥度系数k增大而递增。其主要原因是锥度系数k由0增大到1的过程中，初始缠绕张力由恒张力向恒力矩过渡导致剩余张力的变化逐渐趋于平缓。

(a)T=50 ℃

(b)T=100 ℃

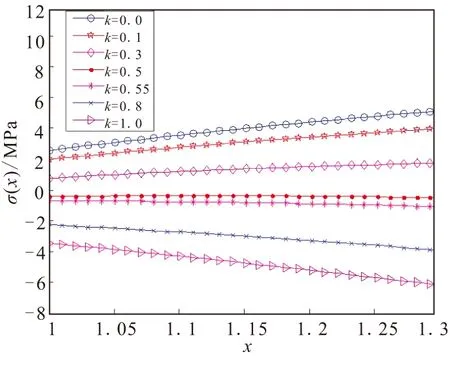
图8 不同锥度系数下线性作用剩余张力分布Fig.8 Distribution of remaining tension in different linear coefficient of taper

图9 双曲锥度张力作用下剩余张力分布Fig.9 Distribution of remaining tension in hyperbolic taper tension

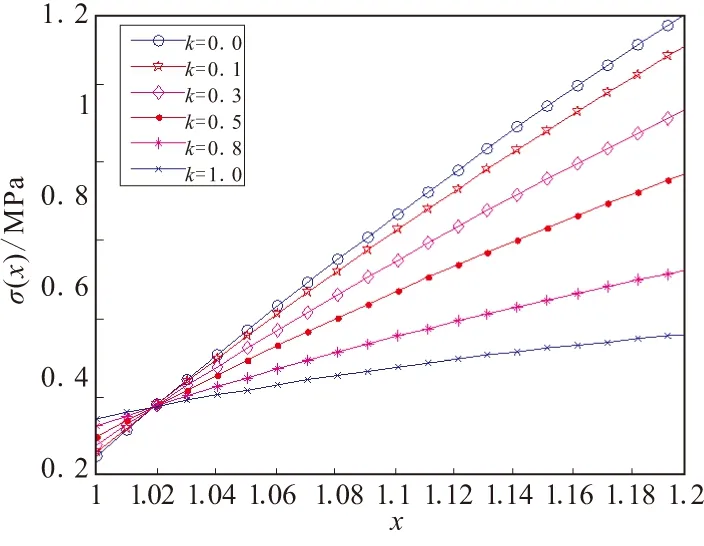
图10 不同锥度系数下双曲作用剩余张力分布Fig.10 Distribution of remaining tension in different hyperbolic coefficient of taper

4 缠绕层等剩余张力分析

根据最佳张力制度选择，要求缠绕制品在固化后为等剩余张力状态，即F(x)=F，同时σr,σθ存在如下关系：

(25)

式中F′为半径r外层所作用的张力。

结合式(21)、式(14)可得设计初始缠绕张力与等剩余张力分布关系：

(26)

文献[12]参数a=250 mm,b=266 mm,rn=314 mm,h=4 mm，在加热温度50 ℃时要实现等剩余张力105 MPa，将各个参数代入式(26)得表1结果。

表1中本文考虑到缠绕过程中温度对剩余张力的影响，缠绕张力低于文献[12]，且各层前后变化平缓，更容易实现缠绕张力的稳定控制。对比文献[13]，结果较为一致，但本文方法可直接得出结果，不需要迭代计算，更为方便。

5 结论

(1)对比恒张力缠绕、恒力矩缠绕和锥度张力缠绕3种典型缠绕张力下剩余张力分布情况，剩余张力随芯模内、外径比λ的增大而减小，随缠绕层半径x的增大而递增；同时随加热温度的升高而减小。

(2)在线性锥度张力作用下，锥度系数k增大到某一值时，剩余张力从单调递增变为单调递减，且锥度系数值越大，最初缠绕层越不易发生褶皱，在线性锥度下存在某一临界值是缠绕制品可达到等剩余张力状态。

(3)本文计算方法考虑芯模变形和加热温度的影响，得出的缠绕张力和剩余张力计算公式更贴合实际结果。

表2 等剩余张力设计：文献[12-13]与本文对比Table2 Design of equal residual tension: contrast to literature [12-13]

[1] 益小苏,杜善义,张立同.复合材料手册[M].北京：化学工业出版社，2009:761.

[2] 沈观林.复合材料力学 [M].北京:清华大学出版社,2006.

[3] 阎龙,史耀耀,段继豪.先进树脂基复合材料制造技术综述 [J].航空制造技术,2011(3):55-58.

[4] 史耀耀,阎龙,杨开平.先进复合材料带缠绕、带铺放成型技术 [J].航空制造技术，2010(17):32-36.

[5] 史耀耀,严新民,唐虹.数控布带缠绕机的设计与开发[J].机械设计与制造工程,1999( 1):10-12

[6] Lu Haibo,Schlottermuller M,Himmel N.Effect of tape tension on residual stress in thermoplastic composite filament winding [J].Journal of Thermoplastic Composite Materials,2005,18(6):469-487.

[7] Bakaiyan H.Analysis of multi-layered filament-wound composite pipes under combined internal pressure and thermomechanical loading with thermal variations[J].Composite Structures,2009(88):532-541

[8] 吴德会,张忠远.厚壁复合材料管纤维缠绕张力的神经网络设计方法[J].复合材料学报， 2012.28(4):195-203.

[9] 文琼华,王显峰,等.温度对预浸料铺放效果的影响[J].航空学报， 2011,32(9):1740-1745.

[10] 段玉岗,刘芬芬,等.纤维铺放压紧力及预浸带加热温度对复合材料力学性能的影响[J].复合材料学报，2012.8

[11] 刘成旭,邢静忠,陈利,等.柔性厚壁筒环向缠绕张力分析与设计[J].固体火箭技术,2013,36(2):261-265.

[12] 朱国辉,郑津洋．新型绕带式压力容器[M〗．北京：机械工业出版社.1995：85-90．

[13] 任明法,郑长良,陈浩然.具有内衬的缠绕容器缠绕层等张力设计的迭代搜索[J]．复合材料学报，2004，21(5):153-158．

(编辑：薛永利)

Composite winding tension design based on the influence of temperature and mandrel deformation

ZHANG Jun,SHI Yao-yao,KANG Chao,ZHANG Xiao-yang
(Key Laboratory of Contemporary Design and Integrated Manufacturing Technology,Ministry of Education,Northwestern Polytechnical University,Xi'an 710072,China)

Based on the requirements of the process parameters in composite filament winding, aiming at the effect of mandrel deformation and heating temperature on the distribution of winding layers in winding process,the mathematical model of winding tension was established.The analytical model of temperature-induced stress distribution in winding layers as well as the stress distribution of inner layers and mandrel under the outer pressure was investigated.Based on three typical tension winding models,the influence of the mandrel diameter ratio and taper tension coefficient on remaining tension was researched and the theoretical relationship of initial winding tension and temperature was proposed to achieve the equal remaining tension.The analytical solution was based on existing literature;while the deformation of mandrel and influence of temperature was taken into account.The results can be used for the stress analysis of curing and the design of winding tension.

remaining tension;mandrel deformation;thermal stress;tension distribution

2014-07-11；

：2014-08-06。

国家自然科学基金项目(51375394)。

张军(1989—)，男，硕士，主要从事复合材料缠绕铺放工艺及装备研究。E-mail：zjdamon@sina.com

史耀耀(1959—)，男，教授，研究方向为机电一体化装备。E-mail：shiyy@nwpu.edu.cn

V258

A

1006-2793(2015)04-0573-07

10.7673/j.issn.1006-2793.2015.04.023