某型导弹固体发动机喷管防水板结构优化设计

陈 科，任全彬，尤军峰，王立强

(中国航天科技集团公司四院四十一所，西安 710025)



某型导弹固体发动机喷管防水板结构优化设计

陈 科，任全彬，尤军峰，王立强

(中国航天科技集团公司四院四十一所，西安 710025)

用人工神经网络算法，对某型导弹固体火箭发动机喷管防水板结构的5个参数进行了研究。模拟得到了防水板在中心受到φ150 mm、大小为10 t压头的最差工况下的变形与应变，并与试验对比验证数值模拟的正确性。以防水板最大主应力和最小质量为目标函数，获得了目标函数随设计变量的曲线关系，并对参数进行了灵敏度分析。优化能有效减轻防水板质量，较传统设计方法使其质量下降了45.95%，优化结果可指导发动机防水板结构的优化设计。

人工神经网络算法；有限元静力分析；喷管防水板；结构优化

0 引言

在潜射导弹发射过程中，固体发动机喷管防水板起着至关重要的作用，是保证导弹成功发射不可缺少的部件。首先，防水板需要承受导弹发射过程中的弹射载荷作用；其次，发射过程中由于空泡效应而形成高压水柱，防水板同样需要承受这一高压水柱的拍击作用；最后，防水板还需保证发动机点火之前喷管内无水介质的存在，防止点火瞬间燃气流与尾涌喷流耦合产生过大的反作用力[1]。同时，在导弹总体设计中，必须在满足总体设计要求的前提下，尽可能降低消极质量。因此，合理设计防水板结构的设计参数，对保证导弹成功发射及提高导弹综合性能都有重要意义。

1 仿真分析基本理论

1.1 人工神经网络

人工神经网络(artifical neural networks，以下简称ANN)系统是模仿人脑工作方式而设计的一种系统[2]。ANN系统的优点是可有效模拟复杂的高度非线性系统。图1给出了ANN的基本单元的神经元模型,它有3个基本要素：(1)一组连接；(2)一个求和单元；(3)一个非线性激活函数。此外，还有一个阈值θk。

以上作用可分别用数学式表达为

vk=netk=uk-θk

yk=φ(vk)

式中x1,x2,…,xp和wk1,wk2,…,wkp分别为输入信号及神经元k的权值；uk为线性组合结果。

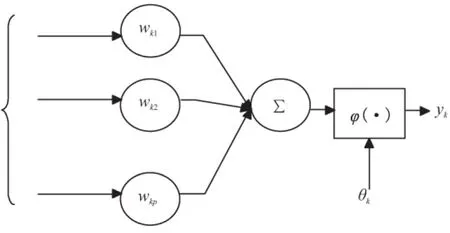
图1 基本神经元模型Fig.1 Basic model of nural cell

1.2 有限元静力强度分析理论

ANSYS是由美国ANSYS公司系统开发和投放市场的一种用于计算机辅助工程的有限元分析程序[3-4]。本文应用ANSYS静力学模块进行数值仿真计算，静力分析是在固定不变的载荷作用下，求解结构的响应[5]。静力学方程为

[K]{u}=[F]

式中 [K]为刚度矩阵；{u}为位移矢量；[F]为静力载荷。

静力分析中，不考虑随时间变化的载荷，忽略惯性力和阻尼。如果假设材料为线弹性，结构变形小，则[K]是常量，求解的是线性静力问题；如果[K]为变量，则求解的是静力非线性问题[6]。

2 优化前防水板的分析

2.1 优化前防水板的结构

本文应用Proe构建的有限元分析模型见图2。防水板由底板、盖板、连接块、加强环和加强筋5个部分组成。连接块将12根加强筋连接起来，与加强环共同起到固定与支撑作用。按照传统设计方法，初始设计盖板与底板厚度同为10 mm，底板直径为1 116 mm，盖板直径为902 mm。加强筋厚度为10 mm，高度为47 mm。加强环外径为902 mm，内径为866 mm。

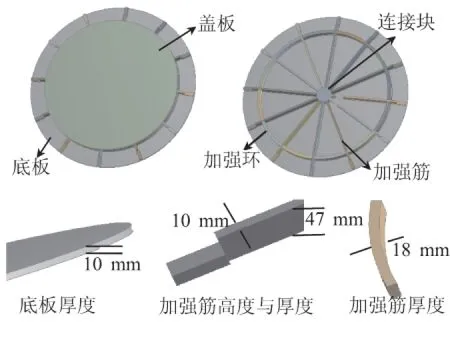
图2 优化前防水板结构Fig.2 Structure of the WB

本文选取了5个主要参数作为设计变量，各参数取值范围列于表1。因为试验过程中，在下盖板上施加了一φ150 mm、10 t的轴向压力压头。所以，以防水板沿轴向的最大应力值和防水板的质量作为目标函数。通过有限元的分析，得到在最大应力小于材料极限强度下防水板的最小质量最佳值。

表1 设计变量参数Table1 Design variables and their ranges mm

2.2 优化前防水板的数值仿真

应用Workbench静力结构模块，对防水板进行强度分析,防水板底板中心φ150 mm处，施加沿轴线100 kN的力。分析得到防水板的总变形如图3所示，防水板的等效应力如图4所示。

图3 优化前防水板总变形Fig.3 Total deformation of the unoptimized WB

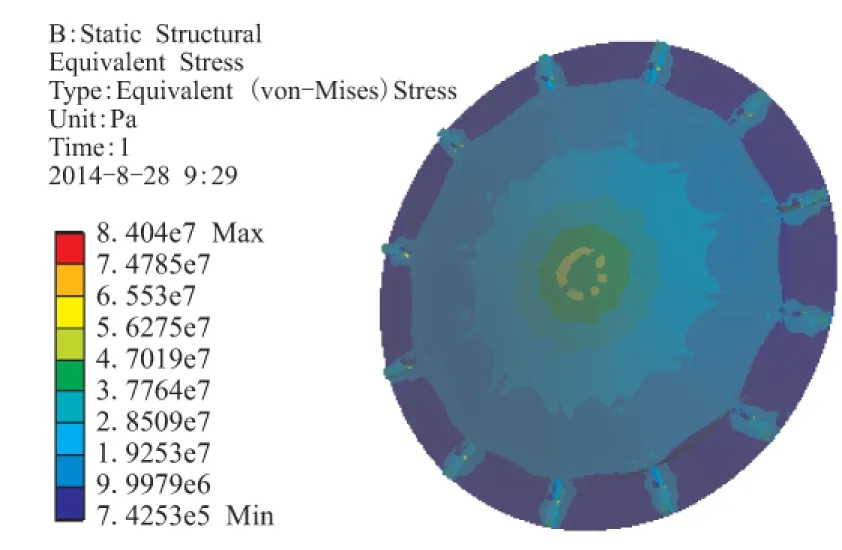
图4 优化前防水板等效应力Fig.4 Equivalent stress of the WB

2.3 优化前防水板静力强度试验验证

2.3.1 静力强度试验

图 5 为防水板承压试验装置图，试验以分级加载的形式对防水板试样施加轴向力。加载分别选择0、5、8、10 t的压头，并实时记录加载过程中测点处的位移和应变值。

试验在防水板的底板、加强筋、盖板上均设置有相互垂直的径向和环向应变片，共计27组54个。其中，每组应变片之间的距离均为100 mm，且上盖板上的3组应变片与底板和加强筋上的3组应变片完全相对应，即应变片的横纵坐标完全相对，只有z方向坐标不同。应变片在实验中的贴片位置见图6。

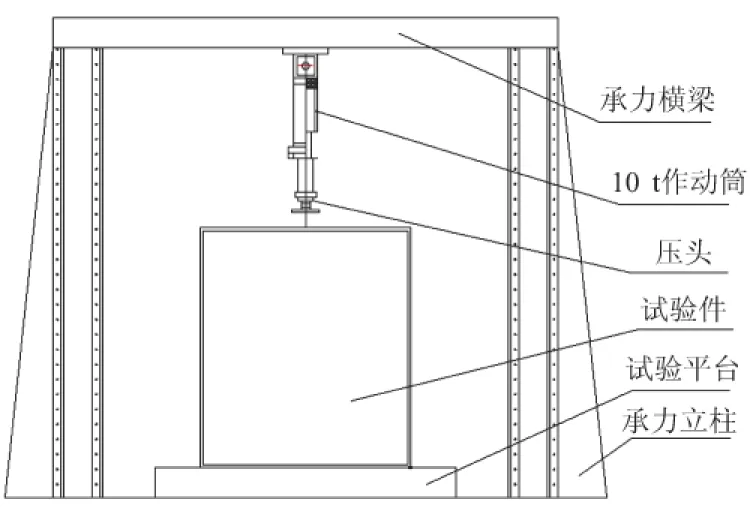
图5 试验装置简图Fig.5 Sketch of the test setup

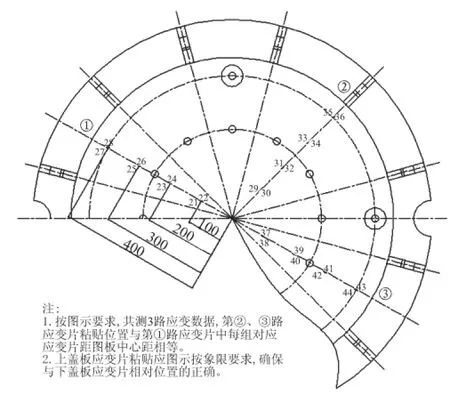
图6 防水板外表面贴片位置示意图Fig.6 Strain gauges locations and variations

2.3.2 算法有效性验证

应用所建立的有限元数值求解方法，对固体发动机喷管防水板进行了仿真计算，并与实验结果进行了对比分析，证明了算法的有效性。

试验过程中沿着不同方向，采用大小不同的压头进行了多次试验。结果表明，在防水板中心位置受到10 t压头作用使防水板变形最严重，会出现焊缝开裂的现象。本文就对防水板变形最大的工况进行模拟，在防水板中心φ150 mm处，施加10 t压力，得出应变片所在位置的变形与应变，并与试验测得的结构进行对比分析。图7即为模拟与试验结构的对比分析图。由图7可看出，模拟与试验应变曲线吻合较好，只是由于计算模型的简化、实验测试仪器误差及外部环境的影响出现微小偏差。综上所述，所建立的数值求解方法能较好模拟防水板在外载荷作用下的真实响应。

3 防水板优化

3.1 设计参数对目标函数的影响

经过仿真计算分析，得到了防水板5个设计变量同目标函数最大应力间的曲线关系，如图8～图12所示。

图8和图9给出了分析模型加强筋高度和厚度对最大应力的响应曲线。相对于原发动机防水板结构，应力值随加强筋的高度和厚度的增大呈近线性下降趋势。也就是说，在不考虑防水板质量的情况下，加强筋的高度和厚度值越大，防水板的结构强度越高，承载能力越强。

(a)盖板上①和③方向的模拟与试验的对比

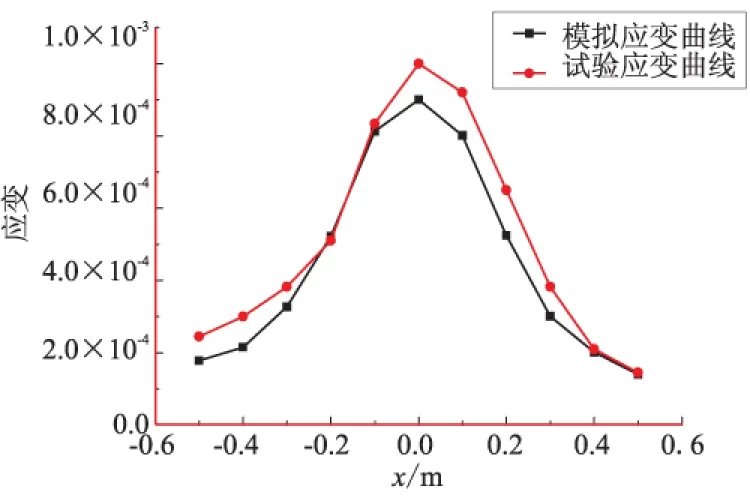
(b)底板上相应的对比

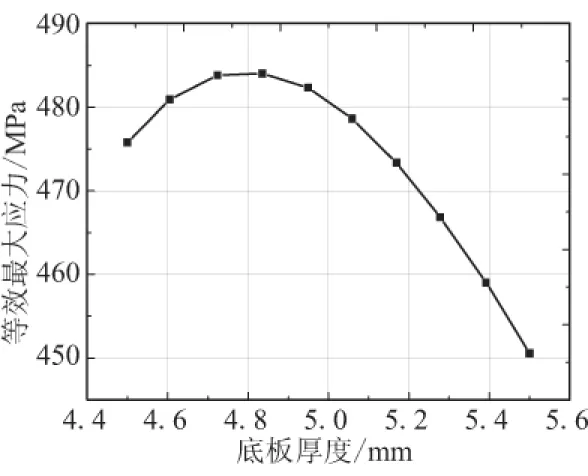
图8 底板厚度h1对目标的响应Fig.8 Baseplate thickness vs targets curve

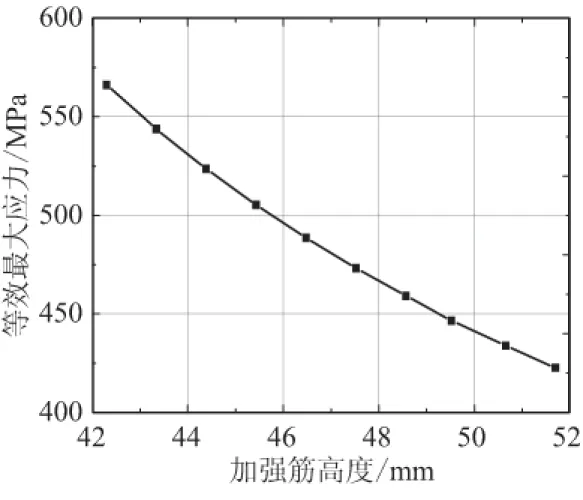
图9 加强筋高度H对目标的响应Fig.9 Dabber height vs target curve

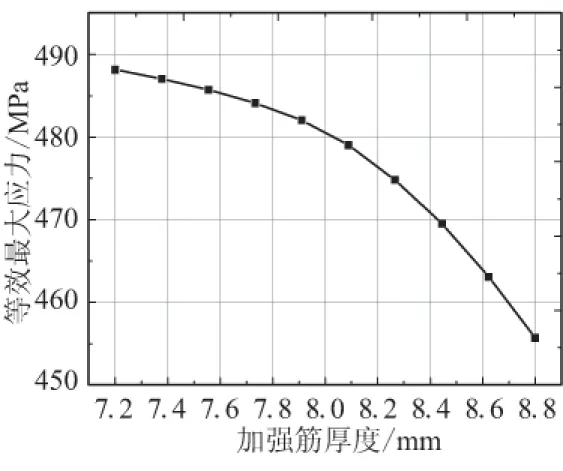
图10 加强筋厚度D对目标的响应Fig.10 Dabber thickness vs target curve

图8和图10～图12表明，对于底板、盖板及加强环厚度的选取，存在最佳值。同时，也看到选取较厚的底板、盖板和加强环，防水板的承载能力会增强。

由仿真结果，结构参数的5个值越大时，防水板强度越高，但防水板重量越重，消极质量会很大，不符合导弹总体设计的要求。因此，在满足设计要求的强度条件下，应尽可能降低消极质量。

图11 外环厚度T对目标的响应Fig.11 Outrace thickness vs target curve

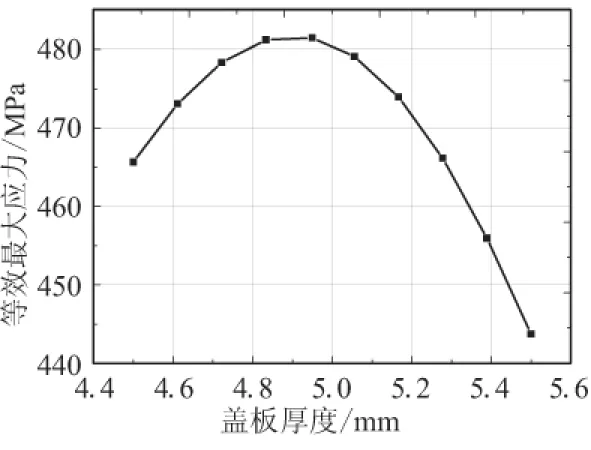
图12 盖板厚度h对目标的响应Fig.12 Coverplate thickness vs target curve

3.2 优化结果

本文在防水板最大应力小于结构极限应力420 MPa的要求下，通过目标驱动优化获得了5个参数的最优值及2组候选值，如表2所示。由表2可看出，第2组候选值结构质量最小，但其最大应力大于结构极限应力，因此不能作为最优值。优化后，防水板结构图如图13所示。

表2 参量优化结果Table2 Optimization results

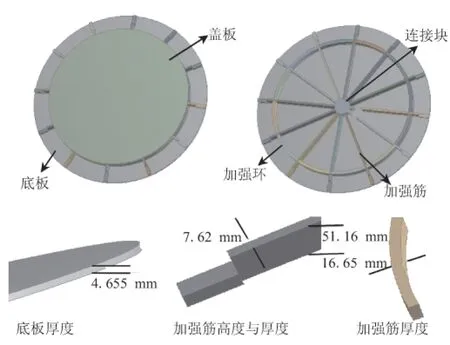
图13 优化后防水板结构Fig.13 Structure of the optimized WB

最后，图14给出了所研究设计变量的灵敏度分配图。由图14可见，相对来说，对提高防水板承载能力有显著作用的参数为加强筋高度、加强筋厚度和外环厚度。在防水板质量比重中起主要作用的参数是底板厚度、盖板厚度和外环厚度。

3.3 防水板优化后的结构强度校核

优化后，防水板各主要尺寸都有了明显减小。因此，需要校核优化后防水板的结构强度。与优化前同样的的约束及受力得到的总变形图如图15所示，等效应力图如图16所示。可看出，优化后变形与优化前相比增大6%，增大幅度较小。优化后，最大等效应力为97.073 7 MPa，相比优化前84 MPa增大了15.5%，但依旧满足设计要求(最大等效应力值低于420 MPa)。

图14 参数(设计变量)灵敏度分配图Fig.14 Parameter influence on objective function

图15 优化后防水板总变形Fig.15 Total deformation of the optimized WB

图16 优化后防水板等效应力Fig.16 Total deformation of the optimized WB

4 结论

(1)优化后变形与优化前相比增大6%，增大幅度较小。优化后最大等效应力为97.073 7 MPa，相比优化前84 MPa增大了15.5%，但依旧满足设计要求(最大等效应力值低于420 MPa)。

(2)对比防水板各主要参数，对提高防水板承载能力有显著作用的参数为加强筋高度、加强筋厚度和外环厚度。底板和盖板厚度对防水板承载能力的影响较小，但二者对结构质量影响较大。

(3)通过优化，可显著降低目标函数值，提高防水板承载性能，同时降低消极质量。通过优化，防水板质量由原来的59.84 kg降低到了32.34 kg，降低了45.95%。

[1] 邢天安.潜艇水下发射反舰导弹的若干问题探讨[J].飞航导弹,1997,21(3)：2-3.

[2] 杨钟瑾，史忠科.神经网络结构优化方法[R].国家自然科学基金项目，2004：005-203.

[3] Sébastien Issanchou,Jean-Pierre Gauchi.Computer-aided optimal designs for improving neural network generalization[J].Neural Networks,2008,21(9):945-950.

[4] 夸克工作室.有限元分析基础篇ANSYS与Mathematica[M].北京:清华大学出版社，2002.

[5] 李人宪.有限元法基础[M].北京:国防工业出版社,2002.

[6] 张洪才.ANSYS13.0 有限元分析[M].北京:机械工业出版社,2011:304-314.

[7] 陈汝训.固体火箭发动机壳体结构分析与设计[M].航天四院研究生教材，1998.

[8] 王立强，任全彬，尤军峰.固体火箭发动机复合材料壳体裙连接区结构数值分析[J].固体火箭技术，2012,35(1)：10-16.

(编辑：崔贤彬)

Structure optimization of waterproof board for the SRM of some missile

CHEN Ke, REN Quan-bin, YOU Jun-feng, WANG Li-qiang

(The 41st Institute of the Fourth Institute of CASC, Xi'an 710025, China)

Five parameters of waterproof board(WB)for the SRM of some type of missile were investigated using artificial neural network algorithm (ANN).The objective function employed in the present work was the max stress and the min mass of the SRM waterproof board which bears a hydraulic pressure.The deformation and the strain of the waterproof board under the force of 10 t at center position were obtained,and the correctness of the numerical simulation was verified by comparing to the experimental results.The objective function vs. design variables curves were plotted,and the parameters sensitivity analysis were carried out.Optimization can decrease the mass of the waterproof board effectively by 45.59% compared to traditional methods.The results obtained can be used as a guidline for the optimal structure design of the SRM waterproof board.

artificial neural network algorithm;finite element static analysis;the waterproof board of the nozzle;structure optimization

2014-09-14；

：2014-12-12。

陈科(1989—)，男，硕士生，研究方向为工程力学。E-mail:573400722@qq.com

V435

A

1006-2793(2015)05-0707-05

10.7673/j.issn.1006-2793.2015.05.019