带扩张观测器的新型滑模导引律
2015-04-22王华吉简金蕾雷虎民马卫东
王华吉,简金蕾,雷虎民,李 解,马卫东
(空军工程大学 防空反导学院,西安 710051)
带扩张观测器的新型滑模导引律
王华吉,简金蕾,雷虎民,李 解,马卫东
(空军工程大学 防空反导学院,西安 710051)
在精确制导问题中,为克服目标机动和弹体动态特性对制导精度的影响,建立了平面内的弹目相对运动模型,在此基础上建立考虑导弹动态特性的制导模型;为提高末制导精度,设计了考虑导弹动态特性和目标机动的自适应滑模导引律;为了实现该导引律,利用带有滤波器的扩张观测器估计视线角速率、视线角加速度、目标机动加速度及其变化率等制导信息。仿真结果表明,扩张观测器收敛速度快、估计精度高,且具有较强的抗干扰能力;在不同机动条件下,所设计的考虑导弹动态特性的含扩张观测器的改进滑模控制律相比于比例导引律、增广比例导引律和滑模导引律具有较好的导引性能。
滑模导引律;扩张观测器;自动驾驶仪;导引精度
0 引言
在未来战争中,高速机动目标将成为现有导弹防御体系的主要威胁[1],为迎接挑战,越来越多的国家重视对具有拦截高速机动目标能力的新一代寻的导弹研制,而提高末制导精度成为关键问题。变结构控制因具有抗干扰和抗参数摄动的特性,使得它在导引律设计中得到广泛应用。而目标的逃逸机动和弹体动态特性是影响制导性能的重要因素[2],一般的变结构导引律在设计中没有考虑弹体动态特性[3];同时,也将目标机动视为外界干扰来处理,从而因切换项参数选择不当造成抖振现象。
为提高制导性能,本文设计了考虑弹体动态特性和目标机动的变结构导引律。由于导引头无法测量目标机动,所以需要对目标机动加速度进行估计。而观测器在制导信息的估计中得到很好地应用。李雅静等[4]在导弹视线角和视线角速率可测情况下,提出了多状态相关系数矩阵加权组合的方案,对CB观测器进行了改进,用于估计弹目相对距离、相对速度和目标机动加速度。姚郁等[5]将目标机动加速度当作不确定性扩张成新的一阶状态,设计了扩张状态观测器来观测系统状态和估计目标加速度。马克茂等[6]针对末制导过程中制导信息的获取问题,设计了高增益观测器对视线角速率和目标机动加速度进行了估计,取得很好的估计效果。扩张观测器(extended state observer,ESO)是一种非线性状态观测器,是自抗扰控制的重要组成部分。通过把系统中的内外扰动扩张成系统新的一阶状态,再利用特定的非光滑非线性误差反馈,适当选择观测器参数,得到系统所有状态的观测值[5]。
本文采用雷达导引头,假设弹目距离、弹目距离变化率、视线角和视线角速率可测量得到。将系统中的机动目标加速度当作不确定性,并扩张成新的一阶状态,设计了二阶扩张状态观测器来观测系统状态;采用带有滤波器的扩张状态观测器来估计制导信息,然后对所设计的新型滑模制导律进行了实现。仿真结果显示,扩张观测器估计精度高、收敛速度快、具有较强的抗干扰能力,并将估计值应用到制导律的实现,取得了不错的效果。
1 导弹-目标相对运动关系
为研究方便,假设导弹在飞行过程中不发生滚转,将导弹在三维空间中的运动解耦成纵向平面运动和侧向平面运动。由于侧向平面的运动与纵向平面的运动类似,本文仅针对纵向平面拦截情况进行分析。纵向平面的弹目相对运动关系如图1所示。图1中,Vm、Vt分别为导弹与目标的速度;am、at分别为导弹和目标的加速度大小;θm、θt分别为导弹和目标的弹道倾角;R为弹目相对距离;q为弹目视线角;矢量iL、jL为惯性坐标系上的单位方向矢量。
由图1可得,弹目相对运动学模型:
(1)
(2)
(3)
(4)
其中

(5)
(6)
2 考虑导弹动态特性的滑模制导律设计
导弹自动驾驶仪十分复杂,假如将其直接引入到导弹制导律的设计中,将使制导律的设计变得过于复杂而无法完成。为了兼容制导律的设计难度和真实情况的逼近度,本文将导弹自动驾驶仪简化为一阶惯性环节。
2.1 制导模型推导
若将导弹自动驾驶仪考虑成一阶惯性环节,则导弹制导指令和实际过载关系为
(7)
将上式变换到时域有
(8)
又由于
(9)
为便于分析,综合式(6)、式(8)和式(9)得到
(10)
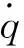
对式(10)第2式求导得
(11)
由式(8)和式(11)得
(12)
(13)
在视线坐标系下,导弹和目标的相对加速度为
a=(atR-amR)iL+(atq-amq)jL
(14)
对式(14)求导得
(15)
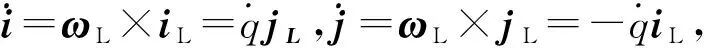
(16)
(17)
(18)
由式(13)得
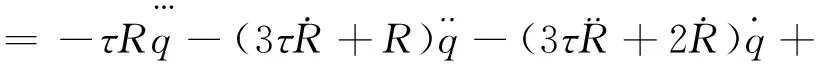
(19)
将式(19)写成矩阵形式为
(20)
其中
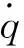
2.2 新型滑模导引律的设计
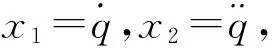
(21)
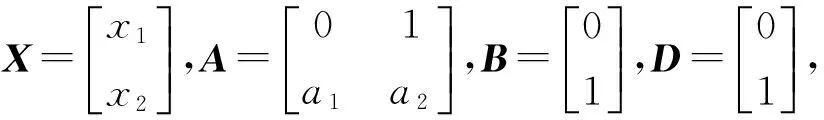
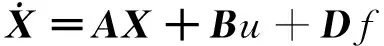
(22)
选取滑模面为
S=CX,C=[c1c2]
(23)
为保证系统状态能到达变结构,且到达的过程中有优良的动态特性,本文采用趋近律方式推导导引律。由于式(22)所示系统为时变系统,所以构造了对时变参数具有自适应能力的变结构趋近律,即
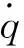
对式(23)求导得
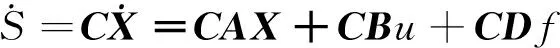
(24)
则
(25)
将上面a1,a2,f和c2=1代入式(25)得
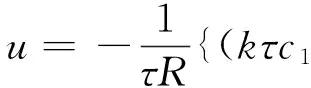
(26)
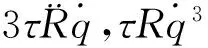
(27)
本文采用高增益连续函数S/[|S|+δ]代替符号函数sgn(S),实现准滑动模态控制[11],可有效地消弱抖动。
3 带滤波器的扩张观测器设计
3.1 扩张观测器
(28)
其中,Vq为系统状态量;amq为控制量;atq为系统中的未知干扰;y为系统的可测输出,若将atq作为系统的扩张状态,则新系统为[7]
(29)
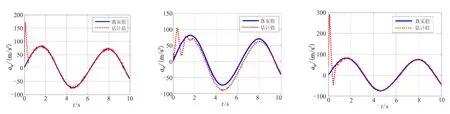
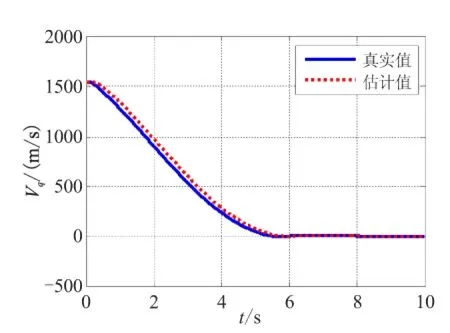
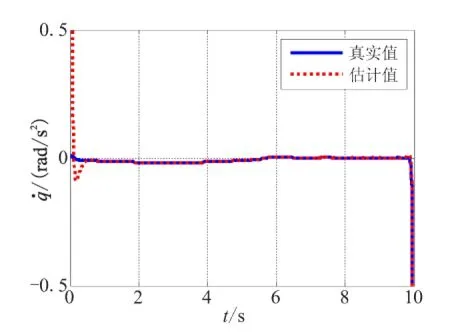
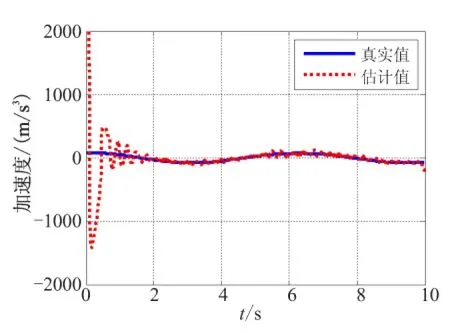
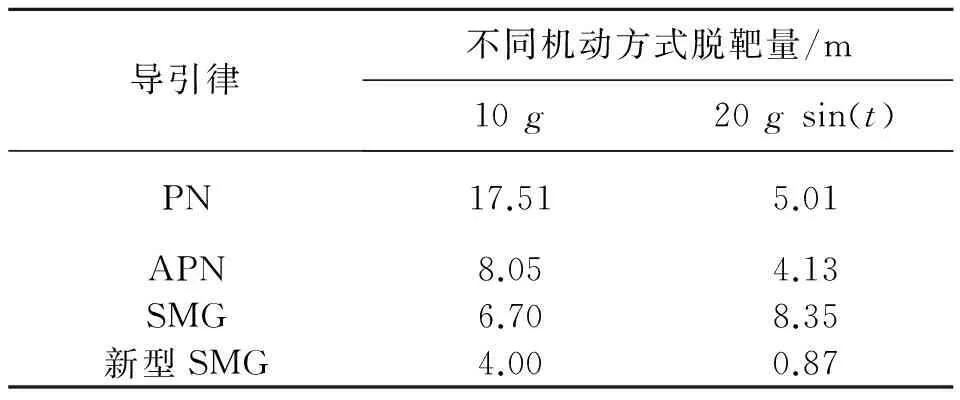
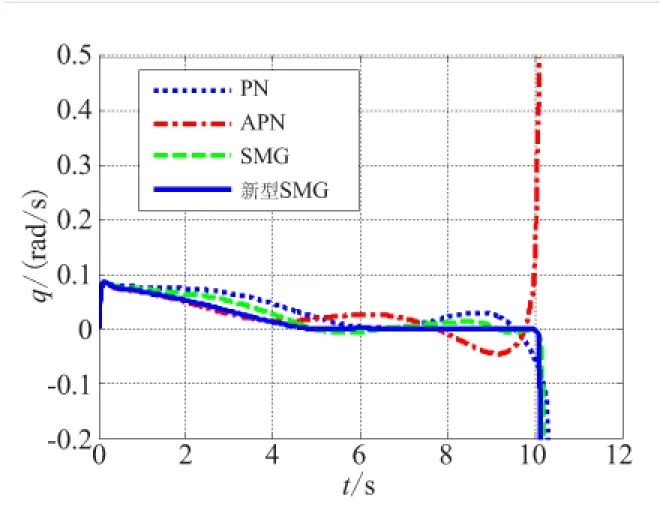
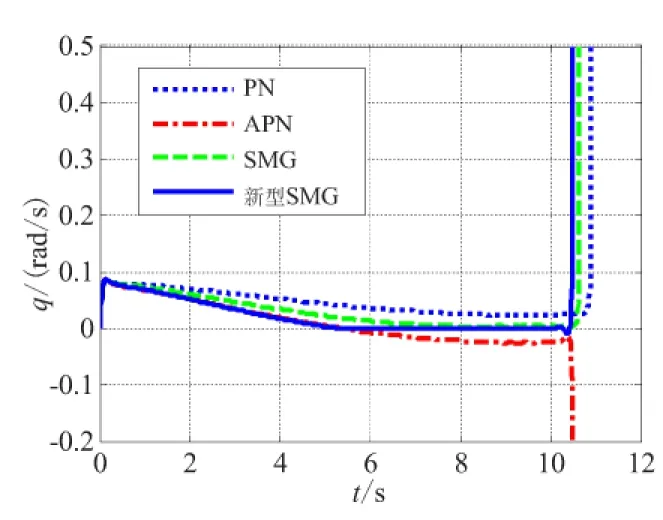
这里g(t)是目标加速度atq的导数,形式也是不确定的。当g(t)有界,即|g(t)| (30) 这里E1是扩张观测器的估计误差,Z1和Z2是观测器的输出,β01、β02是观测器的增益,函数fal(·)定义如下: (31) 0 3.2 带有滤波器的ESO设计 由于滤波器的结构是自定的,所以它的方程就是确定的。如果对滤波器与原系统组成的复合系统构造ESO,组成扩展形式的ESO,就可解决量测噪声的问题。在ESO中包含滤波器方程,可计及滤波器对原输出信号的影响,且考虑到高阶ESO参数整定较为困难,为设计方便选择一阶滤波器。 由于实际系统中,在输出的量测时,不可避免地会受到噪声干扰。所以,通过设计滤波器对其进行滤波处理然后,再输入到观测器。假设 (32) 式中Vq为带有量测噪声的系统状态;Vqfilter是经过滤波后的系统状态;τ1为滤波器的时间常数。 对系统(29)进行扩张一阶状态,用以描述滤波器方程,则得到复合系统的状态方程如下: (33) 现在系统的输出y为滤波后的信号,已经去除了噪声的影响。此时可构造如下ESO: (34) 上式采用滤波后的信号Vqfilter作为输出,通过反馈对观测器进行校正。由于Vqfilter中已经不含噪声信号,因此这种形式的ESO可消除量测噪声对系统观测的影响。 3.3 ESO参数的选取 ESO参数的选取直接影响着它的估计效果,通过ESO系统的稳定性进行分析,可得到ESO参数的选取的原则[8]。通过构造分段Lyapunov函数,分析观测器(30)对系统(29)观测误差的收敛性[9]。选择合适的观测器参数,可控制观测误差的范围: (35) (36) 其中,k、c为大于1的正数。由于fal为幂函数,且α<1,当E1>δ时,存在 (37) 若β02(c-1)>kcg0,则α越小,观测器对误差的抑制作用越大。当g(t)较小时,由式(35)和式(36)可知,β01、β02选择不用太大,就可补偿观测器的估计值;当 较大时,为了使估计更加准确,就需要选择更大的β01、β02,但并不是越大越好,当选择过大,会导致估计值振荡。对于观测器(34)参数的选择原则和观测器(30)相似,但β00、β01、β02、α1、α2、δ1和δ2具体值的确定通过多组仿真对比来完成。 通过仿真可知,β00选择过大,估计值会发散,β00选择过小,估计值会振荡;β01选择过大,估计值会出现延迟,β01选择过小,估计值会振荡;β02选择过大,收敛速度慢,β02选择过小,估计值的幅值变小。 3.4 ESO的估计结果 (a)情形1 (b)情形2 (c)情形3 图3 Vq的估计结果Fig.3 Estimation values of Vq 图4 视线角加速度的估计结果Fig.4 Estimation values of the derivative line-of-sight rate acceleration 由图2可知,噪声对ESO的估计效果造成了很大的影响,低通滤波器使得滤波值和真实值出现了一定偏差,从而导致ESO估计结果不理想。通过对比可知,利用带有滤波器的新型ESO估计目标机动效果良好。由图3~图5可知,采用新型ESO所估计的制导信息效果良好。 图5 加速度的估计结果Fig.5 Estimation values of the derivative of acceleration ESO的参数取值为β00=30、β01=100、β02=500、α1=0.85、α2=0.3、δ1=0.1、δ2=0.1。 表1 导弹采用4种导引律平均脱靶量的对比Table1 The contrast of mean miss distance with four different guidance law 图6 常值机动下视线角速率的对比Fig.6 Contrast of line-of-sight rate with constant maneuver 图7 正弦机动下视线角速率的对比Fig.7 Contrast of line-of-sight rate with sine maneuver 由表1可知,无论APN还是新型SMG,在拦截较大机动目标时,由于对导引律进行目标机动补偿,所以制导性能都有所提升,而文中所设计的制导性能最优。由图6和图7可知,相比于其他3种导引律,新型SMG的视线角速率收敛最快。 (1)建立考虑导弹动态特性的制导模型;基于此模型,设计了考虑导弹动态特性和目标机动的自适应滑模导引律。 (2)为了实现所设计的导引律,采用带有滤波器扩张状态观测器估计制导信息。其中,包括视线角速率、视线角加速度、目标机动加速度及其变化率。然后,将估计所得的信息应用到所设计的新型滑模导引律中。 (3)仿真研究表明,带有滤波器的扩张状态观测器相比于一般扩张观测器具有收敛速度快、估计精度高、抗干扰能力强的优点;所设计的新型滑模导引律的视线角速率收敛速度明显提升,从而提高了制导精度。 [1] 姚郁,季登高,马克茂. 关于精确末制导系统总体设计的综合考虑[J].红外与激光工程,2008,37(3):382-385. [2] Zarchan P. Tactical and strategic missile guidance[M]. AIAA Inc, Reston, VA, USA, 3rd Ed, 1997:135-140. [3] 马克茂,马杰.机动目标拦截的变结构制导律设计与实现[J].宇航学报,2010,31(6):1589-1594. [4] 李雅静,侯明善,熊飞.一种改进的观测器算法在制导中的应用[J].宇航学报,2010,31(8):1920-1926. [5] 姚郁,王宇航. 基于扩张状态观测器的机动目标加速度估计[J]. 系统工程与电子技术,2009,31(11):2682-2692. [6] 马克茂,贺风华,姚郁.目标机动加速度的估计与导引律实现[J].宇航学报,2009, 30(6): 2213-2219. [7] Zhu Zheng, Xu Dong, Liu Jing-meng. Missile guidance law based on extended state observer[J]. Ieee Transactions on Industrial Electronics,2013,60(12):5882-5891. [8] 王宇航,姚郁,马克茂. 二阶扩张状态观测器的误差估计[J].吉林大学学报, 2010,40(1): 143-147. [9] 黄一,韩京清.非线性连续二阶扩张状态观测器的分析与设计[J].科学通报,2000, 45(13): 1373-1379. [10] 林飞,孙湖,郑琼林. 用于带有量测噪声系统的新型扩张状态观测器[J].控制理论与应用,2005,22(6):995-998. [11] 周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002:8-26. (编辑:薛永利) A new sliding mode guidance law based on extended state observer WANG Hua-ji, JIAN Jin-lei, LEI Hu-min, LI Jie, MA Wei-dong (Air and Missile Defense College, Air Force Engineering University, Xi'an 710051, China) To overcome the effect of target maneuvering and dynamic characteristics as guidance accuracy in guidance process, a guidance model with dynamic characteristics considered was firstly established. Based on the model, an adaptive sliding mode guidance law consideriny dynamic characteristics and target maneuvering was designed. Then, an extended observer was used to estimate the guidance message such as the rate of line-of-sight (LOS), acceleration of LOS, maneuvering acceleration and acceleration rate of target. The result of simulation shows that the extended observer has fast speed of convergence, high accuracy of estimation and good ability of anti-jamming. The guidance law designed has better guidance performance than that of proportional navigation guidance (PNG), augmented proportional navigation guidance (APNG)and sliding mode guidance (SMG)in different conditions of target maneuvering. sliding mode guidance;extended state observer;autopilot;guidance accuracy 2014-07-14; :2014-08-11。 航空科学基金(20130196004)。 王华吉(1988—),男,硕士,研究方向为飞行器制导与控制。E-mail:574095241@qq.com V448.15 A 1006-2793(2015)05-0622-06 10.7673/j.issn.1006-2793.2015.05.004
4 仿真验证
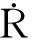
5 结论
