Guidance law with angle constraint used to intercept maneuvering targets①

LI Xian-qiang，ZHOU Jun

(Institute of Precision Guidance and Control, Northwestern Polytechnical University,Xi'an 710072,China)



Guidance law with angle constraint used to intercept maneuvering targets①

LI Xian-qiang，ZHOU Jun

(Institute of Precision Guidance and Control, Northwestern Polytechnical University,Xi'an 710072,China)

A continuous finite-time stabilization guidance law with terminal impact angle constrained is presented in this paper,which can be used to intercept the non-maneuvering and maneuvering target.Firstly,an adaptive super-twisted algorithm is designed based on the super-twisted algorithm,which can effectively alleviate the chattering,through using the adaptive parameters.A finite-time stabilization disturbance compensator is designed based on the adaptive super-twisted algorithm and the integrated sliding surface.Secondly,the geometric homogeneous theory is employed to design the finite-time stabilization controller for the compensated nominal system.The controller,composited by above disturbance observer and the geometric homogeneous theory controller,can ensure the system's finite time convergence.In addition,the composite controller is continuous and the parameters are adaptive,which can effective suppress the chattering of the sliding mode.The above control theory is applied to design the guidance law with terminal impact angle constrained,and the effectiveness of the guidance law is verified through simulation.

terminal impact angle constrained;guidance law;finite-time stabilization;sliding mode

0 Introduction

In modern warfare,not only a small miss distance is required for the missiles, and in order to enhance the attacking effectiveness,but also certain impact angle constraints are also needed to be met[1].Such as inverse trajectory interception is always employed to enhance the matching efficiency of fuse and warhead.And the desired direction of the velocity vector of the missile should be opposite to that of the target. In order to enhance the penetration effect when attacked fortification,the missile needs to attack the target in vertically direction.

The sliding mode control possesses the advantages of strong robustness and easy to implement,so it is widely used in the design of the guidance law with impact angle constraint.But for the guidance law with angle constraint designed based on the conventional sliding mode control, only asymptotical stability can be maintained. While the demand of the guidance law with finite-time stability is growing in modern warfare.For example,in the air-combat,the guidance laws with impact angle constraint with finite-time convergence is especially important[4-5].In this regard,some scholars developed lots of corresponding finite-time guidance law based on the terminal sliding mode control theory.For instance,in References[6-7] the conventional terminal sliding mode control theory is used in the development of the finite-time guidance law,while there are singularities in the guidance laws developed in References[6-7],and the guidance command may be saturated in the application.To tackle the singularity issue,the non-singular terminal sliding mode control theory is employed in the development of the finite-time guidance law with impact angle constraint in the References[4-8].However,the finite-time guidance laws, which are developed in the above references,are generally characterized with discontinuity.The discontinuity in the guidance law can cause chattering,which may reduce the guidance accuracy, and even lead to system instability[1].To alleviate the chattering,in Reference[9]a finite-time guidance law is designed based on the high-order sliding mode control theory.In the high-order sliding mode control theory,the control parameter should be chosen greater than the bound of the disturbance.And large control parameters will reduce the chattering suppression effect[10].While in practice,for safety reasons, the actual bound of the disturbance often is chosen larger,so the parameters of high-order sliding mode control are always selected larger.Thus the chattering suppression effect may be degraded.

In this paper,a novel adaptive high-order sliding mode control is developed,in which the control parameters are adaptive to the disturbance.Thus the conservatism in choosing the control parameters can be greatly reduced.And the chattering of the sliding mode control will be greatly alleviated too. Moreover,in this paper the adaptive super-twisting algorithm is combined with the integral sliding mode surface for the first time.And based on this,a finite-time disturbance compensator is designed.Then the geometric homogeneous theory is employed to design a finite-time controller for the compensated system.The controller design method is then used in the designing of the guidance law with impact constraint angle,and a finite-time continuous guidance law is successfully developed.The effectiveness of the designed guidance law is also verified through three-dimension simulation.

1 Preliminaries

1.1 Design of the adaptive super-twisting algorithm

Lemma 1.Super-twisting algorithm[11]Consider the system as following:

(1)

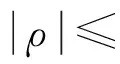
Thesuper-twistingalgorithmproposedinLemma1belongstothehigh-orderslidingmodecontroltheory,inwhichthediscreteswitchingtermhidesintheintegralpartoftheinput,sothechatteringoftheslidingmodecontrolcanbeeffectivelyalleviated.Throughanalysisitcanbeconcludedthatthecontrolparametersofthesuper-twistingalgorithmneedtobelargerthantheboundofthedisturbance.However,thepreciseboundofthedisturbanceisdifficulttobeobtainedinpractice.Andincontrollerdesign,theboundofthedisturbanceisalwayschosenmuchlargerthantheactualvalueofthedisturbance.Andthenthecontrolparametersofthesuper-twistingalgorithmwillbechosenmuchlarger,whichwillmakesthechatteringalleviatingeffectbecomeworse[10].Toensurethechatteringalleviatingeffect,inthissection,thesuper-twistingalgorithmwillbeimprovedandanadaptivesuper-twistingalgorithmwillbedeveloped,inwhich,thecontrolparametersisadaptivetothedisturbance.

Theorem1.Adaptivesuper-twistingalgorithm

Considerthesystemasfollows:

(2)

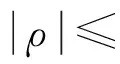
(3)

where,L(t)=r+l,lis a constant andl>0.

(4)

where,γ>0,and

(5)

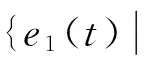
Proof.Thelyapunovefunctionischosenas:

(6)

(7)

here,

(8)

(9)

(10)

Accordingtoequation(8),onecanobtain

(11)

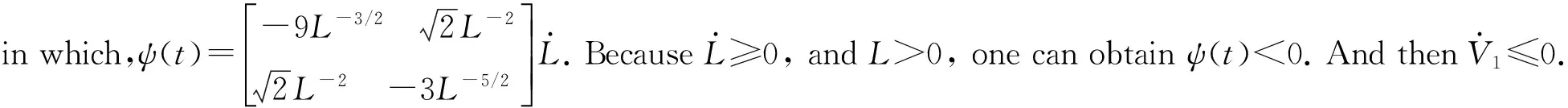
Accordingtoequation(9),onehas

(12)

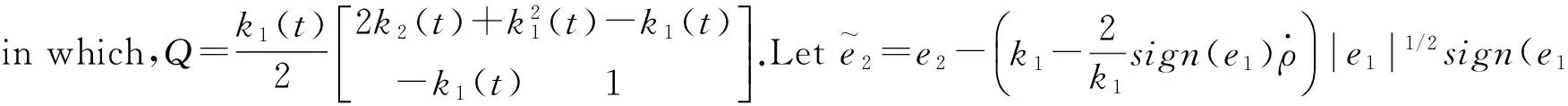
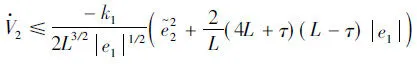
(13)

Notingequation(3)and

L-τ=r+l-τ=l+2r

(14)

thenfromequation(13),wehave

(15)

Formequation(10),weknow

(16)

Substituting(11), (13)and(16)into(7),yields

(17)

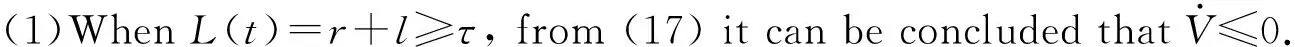
(18)

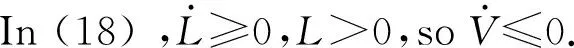
1.2 A finite-time composite control law designed based on adaptive super-twisting algorithm

Consider a system with disturbance as following:

(19)

where,xidenote the states,u=u1+uf,u1denotes the controller of the nominal system,ufdenotes the compensation law,fdenotes disturbance.

For the system above,a compensator will be proposed in the following Theorem 2.

Theorem 2.For the system denoted as (19),when the disturbance compensator is chosen as following:

(20)

where,k1andk1are chosen as those in Theorem 1,and

(21)

Then the sliding mode surfaces1will converge to zero in finite time under the control ofuf.And on the sliding mode surface, the disturbance is nearly fully compensated.So the system on the sliding mode surface can be viewed as a nominal system as following,which is without the disturbance.

(22)

Proof.Firstly,the integral sliding mode surface is designed as following:

(23)

Differentiating the equation (23)and combing with (19),we have

(24)

(25)

According to Theorem 1, we known the reaching law as (25)is able to maintains1which can converge to zero in finite time. Whens1converges to zero,uf+f≈0 can be obtained from (24). And then the system (19)reduces to the nominal system as (22), which is without disturbance.

Remark 1. If the initial value ofx2can be obtained,the approaching process of the sliding mode surface can be eliminated.According to equation (23), the sliding mode surface is improved as following:

(26)

It is obviously that in (26),the initial value of the sliding mode surfaces1is zero,so the approaching process of the sliding mode surface is eliminated.

Remark 2.Through compensation,the disturbed system (19)can reduce to the nominal system (22)in finite time.In the following,a finite-time control law will be designed for the nominal system (22).

1.3 A finite-time controller designed based on geometric homogeneous theory

Consider a kind of integral chain system as following:

(27)

where,xi(i=1,2…,r)are the states,udenotes input.For the system as (27),the following lemma holds.

Lemma 3[12].In equation (27),when the input is chosen as (28),then the states of the system (27)will converge to zero in finite time.

(28)

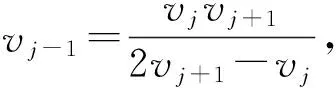
Remark3.AccordingtoTheorem2andLemma3,weknowiftheinputof(19)isdesignedasu=u1+uf,inwhichu1andufaredenotedasequation(20)and(28)separately,system(19)willbefinite-timestable.

2 Modeling

2.1 Modeling of the engagement geometry

The engagement geometry between the missile and the target can be shown as Fig 1.

Fig.1 Engagement geometry

According to the geometry in Fig.1, the modeling equation can be formulated as:

(29)

where,θmdenotes the flight path angle of the missile,θtdenotes the flight path angle of the target.vmdenotes the velocity of the missile andvtdenotes the velocity of the target.Rdenotes the relative distance andqdenotes the angle of the line of sight (LOS).

2.2 Modeling of the impact angle constraint

In the design of the guidance law with impact angle constraint,it is desired that the missile can intercept the target along with a desired direction.So at the impact time,the direction of the missile velocity vector shall meet the following constraint:

θm(tf)=θd

(30)

where,θddenotes the desired flight path angle.If it is desired a head-on interception,thenθd=θt-π.

If it is assumed thatqdis the desired angle of the LOS at the impact time,the following equation holds.

(31)

Such that,one can uniquely determine the desired angle of sight,when the flight path angle of the target and the desired flight path angle of the missile are known.

2.3 Modeling of the LOS rate

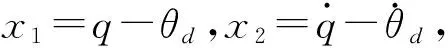
(32)

3 Design of the guidance law

Based on equation (32),the guidance law is designed as following:

u=(-a1x2+ueq+uf)/a2

(33)

Underthecontroloftheequation(33),thesystem(32)willreducetotheequationasfollowing:

(34)

Inequation(34),itisassumedthatueqis the equivalent control law when the system is without disturbance.And it can ensure that the system is finite-time stable,ufis a compensator,which is used to compensate the disturbancef.

3.1 Design of the compensator

In this section,a compensatorufwill be designed,which can fully compensate the disturbancefin finite time.And then the system (34)will reduce to a nominal system without disturbance. Based on Theorem 2,the compensator can be designed as following:

(35)

where,the parameters are selected according to Theorem 1.

(36)

Then,according to Theorem 2,uf+fcan converge to zero in finite time, such that the disturbance can be fully compensated in finite time.And then the system (19)can reduces to the nominal system as following:

(37)

In the following,a finite-time sTablecontrol lawuequwill be designed based on the nominal system.

3.2 Controller design based on the geometric homogeneous theory

In this section,a controller will be designed based on the geometric homogeneous theory.The controller should ensure that the system is asymptotically sTableand possesses suiTablenegative homogeneous degree.And the finite time stability of the system (32)will be achieved when the system (32)is asymptotically sTableand possesses suiTablenegative homogeneous degree.The corresponding controller is designed as follows based on Lemma 3.

(38)

in which,μ1=0.25,μ2=0.4.λ1andλ2are positive constants which can ensure thatp2+λ2p+λ1is Hurwitz.

In summary,combing equations (33),(35),(36)with (38),the guidance law can be obtained as:

(39)

From the guidance law (39),we know that it is continuous nonsingular and finite-time stable.So the saturation cased by singularity can be avoided.And the chattering cased by non-discontinuous sliding mode control can also be avoided.Moreover,the parameters of the compensator are adaptive in guidance law (39),thus it can avoid the performance degradation caused by improperly selected parameters.

4 Simulation

In this section,the guidance law proposed in this paper (ISMCFTGL)will be simulated.And for comparison,the guidance law with impact angle constraint (SMCGL)proposed in reference[1],which is designed based on sliding mode control,will be also simulated. The SMCGL is denoted as:

(40)

In the following,both the case of intercepting constant velocity target and the case of intercepting the maneuvering target will be simulated.

4.1 Simulation for non-maneuvering target

It is desired that the missile can intercept the target along the invere trajectory of the target.In simulation,the position of the interceptor is selected asxm=0,ym=0,zm=0.The parameters relevant to the velocity of the interceptor are selected asvm=400,θ=45°,ψm=-40°.The position of the interceptor is selected asxt=7 500,yt=5 000,zt=4 330.The parameters relevant to the velocity of the target are selected asvt=300 m/s,θt=150°,ψt=150°.

The parameters of ISMCFTG used in longitudinal channel and lateral channel are the same. And they areλ1=4,λ2=4,r(0)=0.5,l=0.6,ε=0.001,γ=15.The parameters of SMCGL in longitudinal channel and lateral channel are the same too. And they areλ=3,k=4,ε=1.

The comparison simulation resultes are decipited as Table1 and Fig.2～Fig.5.

Table1 Miss distance and the angle tracking error when intercepting the non-maneuvering target

Fig.2 Comparison of the trajectories,when intercepting the non-maneuvering target

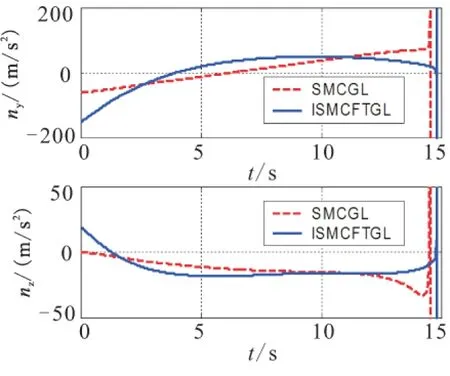
Fig.3 Comparison of the payloads,when intercepting the non-maneuvering target

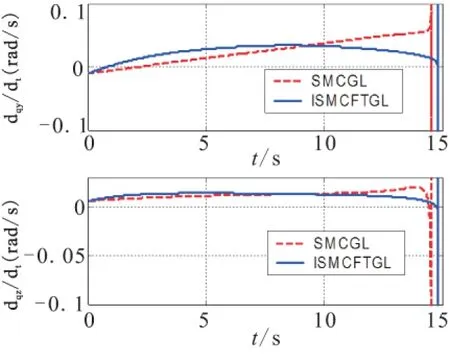
Fig.4 Comparison of the velocity of the line-of-sight, when intercepting the non-maneuvering target

From Fig.4,it can be concluded that, when intercepting the non-maneuvering target, ISMCFTGL can effectively control the LOS rate converge to the neighborhood of zero,while the LOS rate under the control of SMCGL diverges slowly.Therefore,it is verified that the guidance performance of ISMCFTGL is better than that of SMCGL.The advantage of ISMCFTGL is also reflected in Fig.3 and Table1.Such that,the needed overload of ISMCFTGL,at the impact time,is smaller than that of SMCGL(see Fig.3),so that the miss distance is smaller and the tracking accuracy to the desired LOS angle is also higher than that of SMCGL (see Table1).

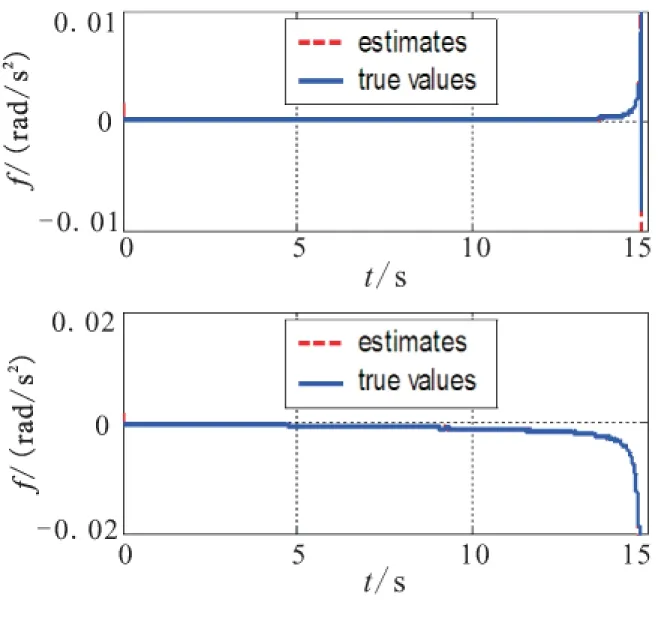
Fig.5 Comparison of the true values and the estimates of the disturbance

In Fig.5,it shows a comparison of the estimated value and the true value of the disturbance in equation (31).Through simulaton results,it can be concluded that the disturbance can be estimated accurately,thus it can maitains the guidance law controls the LOS rate effectively. 4.2 Simulation for maneuvering target

In this section it is also desired that the missile can intercept the target along the invere trajectory of the target.The longitudinal acceleration of the target isatz=50sin(0.8t),and the lateral acceleration isatc=50sin(0.8t).The other parameters are selected the same as those in section 4.1.the simulation results are decipited as Fig.6～Fig.9 and Table2.

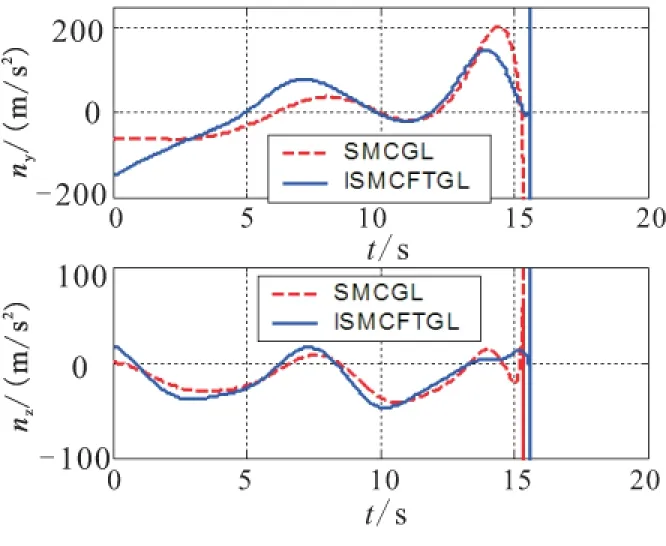
Fig.6 Comparison of the trajectories,when intercepting the maneuvering target

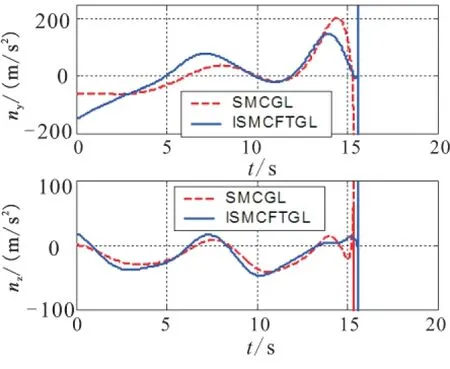
Fig.7 Comparison of the payloads,when intercepting the maneuvering target

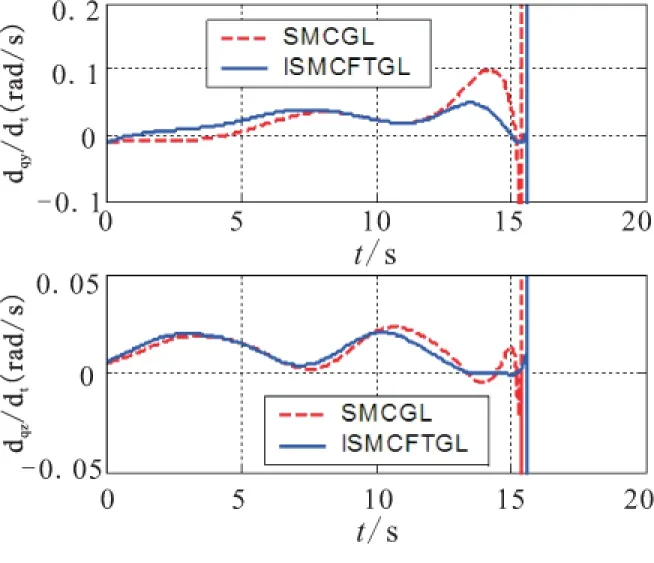
Fig.8 Comparison of the velocities of the line-of-sight,when intercepting the maneuvering target

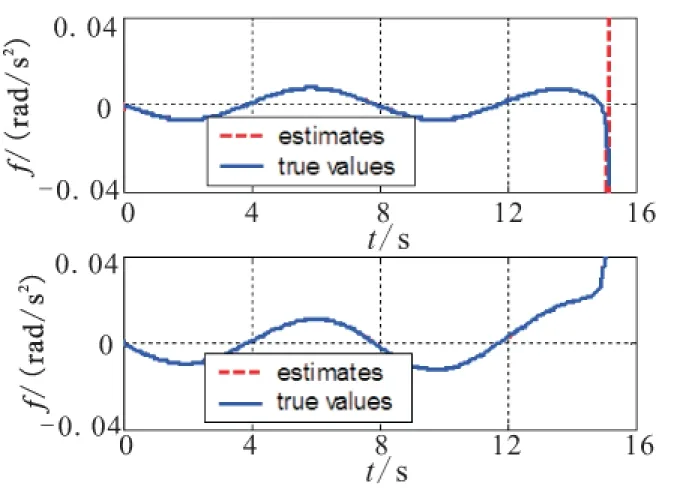
Fig.9 Comparison of the true values and the estimates of the disturbance

Table2 Miss distance and the angle tracking error when intercepting the maneuvering target

According to the simulation results,it can be concluded that the performance of ISMCFTGL in suppressing the LOS rate,in the last paragraph of the interception,is better than that of SMCGL (Fig.8).And the overload of ISMCFTGL is much smaller (Fig.7),which effectively reduce the miss distance and the tracking error to the desired LOS angle (Table2).The reason to obtain such a goog effect is that ISMCFTGL can precisely eatimate the disturbance caused by the accelaration of the target and other factors (Fig.9).And the infulunce to the LOS rate caused by the disturbance can be nearly eliminated completely.Moreover,in the modelling of the LOS rate,the speed characteristic of the target is also fully considered, thus the proposed guidance law ISMCFTGL can effectively intercept the maneuvering target with high speed.

5 Conclusion

In this paper, an adaptive algrithom is firstly proposed through improving the super-twisting algrithom.Then a novel finite-time composite control method is designed through combing with the integral sliding mode surface and geometric homogeneous theory.And the composite control method is then used in designing of the guidance law with impact angle constraint. The proposed guidance law possesses some characteristics as following:

(1)It can not only effectively intercept the non-maneuvering target,but it can also effectively intercept the high maneuvering target.

(2)The guidance law is finite-time stable.

(3)The guidance law is continuous and the parameters are also adaptive.Thus the chattering of the sliding mode conrol is alleviated and the guidance precesion is improved.

[1] CAI Hong,HU zhen-dong,CAO Yuan.A survey of guidance law with terminal impact angle constraints[J].Journal of Astronautics,2010,31(2):315-323.

[2] Kim B S,Lee J G,Han H S,et al.Homing guidance with terminal angular constraint against non-maneuvering and maneuvering targets[R].AIAA-97-3474,1997.

[3] JIA Qing-zhong,LIU Yong-shan,LIU Zao-zhen.Variable-structure backstepping guidance law with terminal angular constraint for video-guided penetrating bomb[J].Journal of Astronautics,2008,29(1):208-214.

[4] Shashi Ranjan Kumar,Sachit Rao,Debasish Ghose.Nonsingular terminal sliding mode guidance with Impact angle constraints[J].Journal of Guidance,Control,and Dynamics,2014,37(4):1114-1130.

[5] Kumar S R,Rao S,Ghose D.Sliding mode guidance and control for all-aspect Interceptor with terminal angle constraints[J].Journal of Guidance,Control,and Dynamics,2012,35(4):1230-1246.

[6] Zhang Y,Sun M,Chen Z.Finite-time convergent guidance law with Impact angle constraint based on sliding-mode control[J].Nonlinear Dynamics,2012,70(1):619-625.

[7] ZHANG Yun-xi,SUN Ming-wei,CHEN Zeng-qiang.Sliding-mode varialble structure finite-time convergence guidance law[J].Control Theory & Applications,2012,29(11):1413-1418.

[8] WANG Hong-qiang,FANG Yang-wang,WU You-li.Research on terminal guidance law of missiles based on nonsigngular terminal sliding mode[J].Systems Engineering and Electronics,2009,31( 6):1391-1395.

[9] DOU Rong-bin,ZHANG Ke.Reserch on termianl guidance for Re-entry vehicle based on second-order sliding mode control[J].Journal of Astronautics,2011,32( 10):2109-2114.

[10] Yuri Shtessel,Mohammed Taleb,Franck Plestan.A novel adaptive-gain supertwisting sliding mode controller:Methodology and application [J].Automatica 2012,48(2):759-769.

[11] Jaime A M.Strict lyapunov functions for the super-twisting algorithm[J].IEEE Transactions on Automatic Control,2012,57(4):1035-1040.

[12] Bhat S P,Bernstein D S.Geometric homogeneity with application to finite-time stability[J].Mathematics of Control,Signals and Systems,2005,17(2):101-127.

(编辑：吕耀辉)

可拦截机动目标的终端角度约束制导律

李宪强, 周 军

(西北工业大学 精确制导与控制研究所,西安 710072)

设计了一种连续且有限时间稳定的终端角约束制导律，该制导律不但能够打击非机动目标而且能有效打击机动性的目标。文中首先将超扭曲算法进行改进，设计了一种自适应超扭曲算法，该算法的参数是随着干扰的大小自动调节的，从而避免了常规的超扭曲算法由于参数选取不当而引起的对滑模抖振的抑制能力下降。文中将自适应超扭曲算法首次与积分滑模相结合，设计了一种有限时间收敛的干扰补偿器，该干扰补偿器能够在有限时间内对干扰进行精确补偿，然后采用几何齐次理论针对干扰补偿后的系统设计了有限时间收敛控制器。以上干扰观测器和控制器组成的复合控制律，能够保证系统的有限时间稳定性，此外该控制律不但是连续的，而且参数是自适应的，因而大大降低了滑模的抖振特性。文中将以上控制理论应用于终端角约束制导律的设计过程中，最后通过仿真验证了该制导律的有效性。

终端角约束；制导律；有限时间稳定；滑模

V448 Do cument code：A Article ID：1006-2793(2015)05-0614-08

10.7673/j.issn.1006-2793.2015.05.003

① Received date: 2015-01-13; Revised date: 2015-04-20。

Foundation: Natural Science of China( 61304238) ; National High-tech R＆D Program of China ( 863) ( 2012AA120602) ．

Biography: LI Xian-qiang ( 1986—) ，man，doctor，speciality: Guidance，navigation and control ( GNC) of vehicle． E-mail: 1740679934@ qq． com