建筑物智能疏散系统最优路径研究

胡治国，贾珍，康全玉，杨俊强

建筑物智能疏散系统最优路径研究

胡治国，贾珍，康全玉，杨俊强

建筑物发生火灾时，为获得能够帮助人员快速、安全撤离的最优疏散路径，根据建筑物内部自身火灾风险及火灾发生时产生的有毒气体等因素的影响，引入当量距离概念，在此基础上建立疏散路径选择模型，采用改进的A*算法快速求取最优疏散路径。选取郑州某大厦进行仿真实验，结果表明，实际距离最短的路径并不是最优疏散路径，同时，最优疏散路径随着有毒气体浓度的变化而相应的变化，这样有利于人员的安全疏散。

最优疏散路径；当量距离；A*算法

0 引言

随着经济的发展，建筑物内部结构愈加复杂，使得火灾的发生也愈加频繁，给人们的生命和财产安全造成了巨大的威胁[1]。火灾发生时，有多条路径可以帮助人员到达安全出口，怎么选择以及选择哪条路径能够使人员快速、安全的撤离[2]是本文讨论的主要内容。

这是一个典型的路径优化问题。建立疏散路径选择模型和目标优化算法是解决路径优化问题的两个重要组成部分[3]。在建立模型方面，国内学者主要基于人员行为[4]、人员差异等影响因素和建筑物特殊结构如出口、楼梯[5]等因素的建模，很少有基于建筑物发生火灾时产生的有毒气体及建筑物本身火灾风险等因素的建模。在目标优化算法方面，大多采用路径搜索能力很强的搜索式算法如：Dijkstra算法[6]、A*算法[7]、Floyd算法[8]。这些算法能得到最优解，同时也都存在着不足，如Dijkstra算法搜索效率低；A*算法空间需求量大；Floyd算法时间复杂度大。

结合上述的研究现状，本文提出在建立疏散路径选择模型时忽略人员行为差异的影响而考虑建筑物内部自身火灾风险及火灾发生时产生的有毒气体等影响因素，并采用改进的A*算法快速求取最优疏散路径。

1 建立疏散路径选择模型

最优的疏散路径应该是在最短的时间内保证人员安全的撤离。由于建筑物内各个因素的综合影响，如障碍物、有毒气体浓度、疏散通道的宽度及建筑物内各个空间火灾危险度等影响，使得距离最短的路径并不是最优的。本文引入“当量距离”[9]的概念来表示实际最短距离和最优路径距离关系，分析并确定上述各个因素对疏散路径的影响并将其相加后与路段的实际距离相乘就是当量距离。那么第i条通道的当量距离表示为公式（1）：

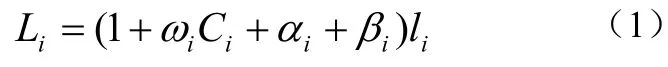
式中：Li表示第i条通道当量距离值，ωi表示第i条通道有毒气体影响人员疏散的惩罚系数，Ci表示第i条路段有害气体体积分数，αi表示考虑障碍物时第 条通道的通行难易系数，βi表示第i条通道所在空间的危险度影响系数，li表示第i条通道的实际距离。

因此，本文采用图论术语描述模型如下：

在图G=(V,E)中，V表示房间和安全出口的集合，V=(V1,V2,...,Vn)，G中的某条弧的权值由该路段的当量距离表示，那么本文的疏散目标表示为公式（2）：

式中：Lmin表示疏散路径选择的目标函数，n表示路径包含的通道个数。

2 当量距离各个系数的确定

根据前面所描述的当量距离的表达式，将分别确定火灾产生有毒气体的影响系数、考虑障碍物时影响系数和不同空间的危险度影响系数。

2.1 火灾产生有毒气体的影响系数确定

火灾燃烧过程中释放大量的烟雾和有毒气体，这些烟气造成的死亡人员占到总死亡人员的75%-80%。在这些烟气中，CO有毒气体是造成人员死亡的主要因素，且不同浓度的有毒气体对人员生命安全的威胁也不尽相同[10]。CO浓度达到250ppm时，人就会感觉到头痛、眩晕等；CO浓度达到1000ppm时，吸入时间超过1小时可使人发生昏迷。CO浓度达到3000ppm时，1小时内可使人致死。由于CO浓度对人员伤害程度是不同的，那么对疏散路径的影响程度也是不同的，故此引入相应的惩罚系数ω[11]，如表1所示：

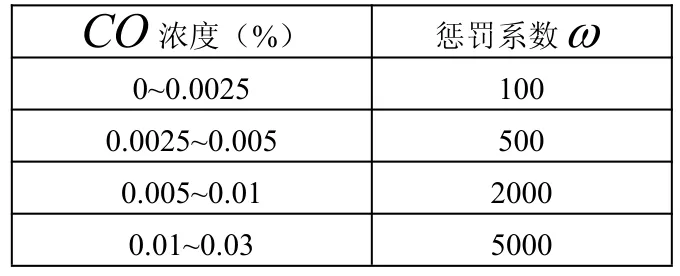
表1 惩罚系数ω

当路段CO浓度越大时，对人员的伤害越大，此时该通道就不适合疏散。相应的，惩罚系数越大，该通道的当量距离就大，在选择疏散路径时就会放弃该通道。

2.2 考虑障碍物时影响系数确定

在选择疏散路径时，通道的通行难易度也是需要考虑的主要因素。它受多种因素影响，如人员密度、人员差异、通道内障碍物的多少，通道的宽度等等。由于本文不考虑人员密度、差异的影响，因此通道通行难易程度由通道的宽度和通道内障碍物的多少决定。影响通道通行难易程度的系数可以表示为公式（3）：

式中：α表示考虑障碍物时路段通道的通行难易系数，r表示建筑物内疏散通道宽度的最小值，一般为1.4m，b表示通道的宽度，2.5是根据最大宽度值3.5和最小宽度值1.4确定的。λ表示障碍物对通行难易度的影响系数[12]，如表2所示：

表2 障碍物对通行难易度的影响系数λ

2.3 建筑物内不同空间的危险度影响系数确定

火灾在发展的过程中有很多不确定的因素，不知道火灾要向什么方向以什么样的速度蔓延，因此选择疏散路径时，除了考虑上述影响外，还应当考虑建筑物内不同空间的火灾风险。火灾风险不仅仅是火灾事故发生概率，更主要的是危害程度和后果[13]。那么危险度影响系数就是根据火灾风险的评估结果，来确定不同危险区域的路段的影响系数。

古斯塔夫法[14]将模糊数学中的方法用于分析各个因子对火灾风险的影响。它先将各个因子表示为火灾危险源的不同特征，再依据这些因子确定火灾危险度GR和人员危险度IR，由此两个因素共同确定建筑物火灾风险。

2.3.1 建筑物火灾危险度计算

基于古斯塔夫提出的各个因子对火灾危险度的影响，GR可以表示如公式（4）：

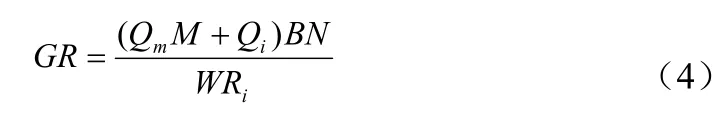
式中：Qm为可移动的火灾负荷因子，M为易燃性因子，Qi为固定的火灾负荷因子，B为火灾区域及位置因子，N为灭火延迟因子，W为建筑物耐火因子，Ri为危险度减小因子，各个因子具体的取值参考文献[15]。

2.3.2 建筑物内人员危险度分析

基于古斯塔夫提出的各个因子对人员危险度的影响，IR可以表示如公式（5）：

式中：k为建筑物内人员特征因子，H为人员危险因子，F为烟气因子，D为人员数量因子，各个因子具体的取值参考文献[15]

2.3.3 火灾危险度的确定

当确定火灾危险分布区域时，首先通过计算求取GR和IR的值，在考虑建筑物内火灾危险度较大和人员危险度较大两个决定因素的基础上确定危险点，划分危险分布区域，如图1所示：

图1 火灾危险分布区域图

一级危险区域发生火灾的可能性大且对人员的伤害大，该区域的路段不适宜作为疏散路径；二级危险区域发生火灾危险的可能性及人员伤害较小，该区域的路段可以作为疏散路径；三级危险区域一般不会发生火灾也不会对人员造成伤害，该区域的路段应当作为疏散路径。由上述可以得出，不同危险区域发生火灾的可能性和对人员伤害程度是不同的[16]，由此确定不同空间的危险度系数β，如表3所示：

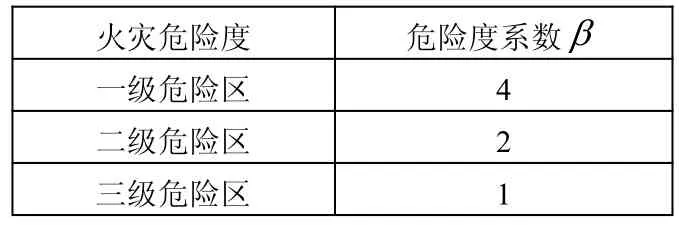
表3 危险度系数β

3 目标优化算法

基于单源点多汇点的大规模网络建立的最优疏散路径问题,要求算法的搜索效率不仅要高而且时间复杂度要小。采用Dijkstra算法时，需要遍历大量节点,搜索效率低；采用A*算法时,搜索效率高但会占用大量的存储空间；采用Floyd算法时,编写代码简单，但应用于大规模网络时时间复杂度高。通过上述的分析，本文在目标优化算法方面选择搜索效率高的A*算法。

A*算法通过评估函数F(n)的值，搜索估价值最小的节点，得到最优路径。每次搜索都要遍寻顺序存储节点信息的整个列表。当节点有几百个或上千个时，反复搜索OPEN表会增加搜索的时间，此时A*算法搜索效率高的优点就不那么明显。针对此问题，采用二叉堆结构存储方式，来提高搜索速度。

在二叉堆[17]中，父节点的值要么大于或等于，要么小于或等于任一子节点的值,同时每个节点的子节点又构成新的二叉堆。它的表现形式为最小二叉堆或最大二叉堆。由于本文使用A*算法是为了寻找最小函数值的节点,因此采用最小二叉堆的方式存储节点。

二叉堆由于它的插入和删除操作方便，大大提高了搜索速度。首先将待插入节点置于数组的末尾，将现在位置1/2处的父节点与之进行值大小比较，若待插入节点值大，就不交换节点位置，反之，则交换节点位置。重复上述过程，直到待插入节点的值大于或等于父节点值停止，当达到堆的顶端时也应停止。

删除节点时，将第一个位置节点移除，将数组末尾的元素移到第一个位置。然后将它和两个子节点的值进行比较，若子节点的值小，就交换位置。重复上述过程，直到节点的值小于或等于子节点的值时停止，当到达堆的底端时也应停止。

若网络中有10000个节点，采用插入排序法时，要将新待插入元素放到合适的位置平均要做500次左右的比较。使用最小二叉堆存储时，只需3～5次计较便能将其插入合适的位置。通过上述分析比较可以看出在同一数量节点的网络中，采用二叉堆存储方式的搜索效率是采用插入排序法的100倍[17]。

4 仿真实验结果与分析

本文以郑州某商厦的第二层为研究对象，绘制其简单的结构路网图，如图3所示：

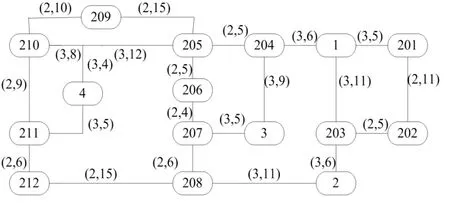
图3 研究对象的路网结构图

图中有201～212共12个房间，1～4个安全出口。(m,n)表示通道的宽度和长度。各个房间统计的数据及GR和IR的计算结果如表4和表5所示：

表4 建筑物GR的计算结果

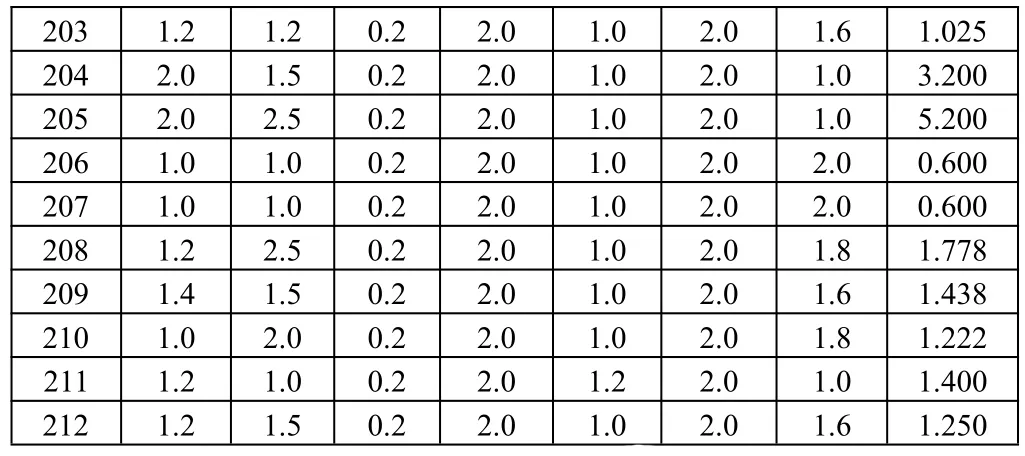
203 1.2 1.2 0.2 2.0 1.0 2.0 1.6 1.025 204 2.0 1.5 0.2 2.0 1.0 2.0 1.0 3.200 205 2.0 2.5 0.2 2.0 1.0 2.0 1.0 5.200 206 1.0 1.0 0.2 2.0 1.0 2.0 2.0 0.600 207 1.0 1.0 0.2 2.0 1.0 2.0 2.0 0.600 208 1.2 2.5 0.2 2.0 1.0 2.0 1.8 1.778 209 1.4 1.5 0.2 2.0 1.0 2.0 1.6 1.438 210 1.0 2.0 0.2 2.0 1.0 2.0 1.8 1.222 211 1.2 1.0 0.2 2.0 1.2 2.0 1.0 1.400 212 1.2 1.5 0.2 2.0 1.0 2.0 1.6 1.250

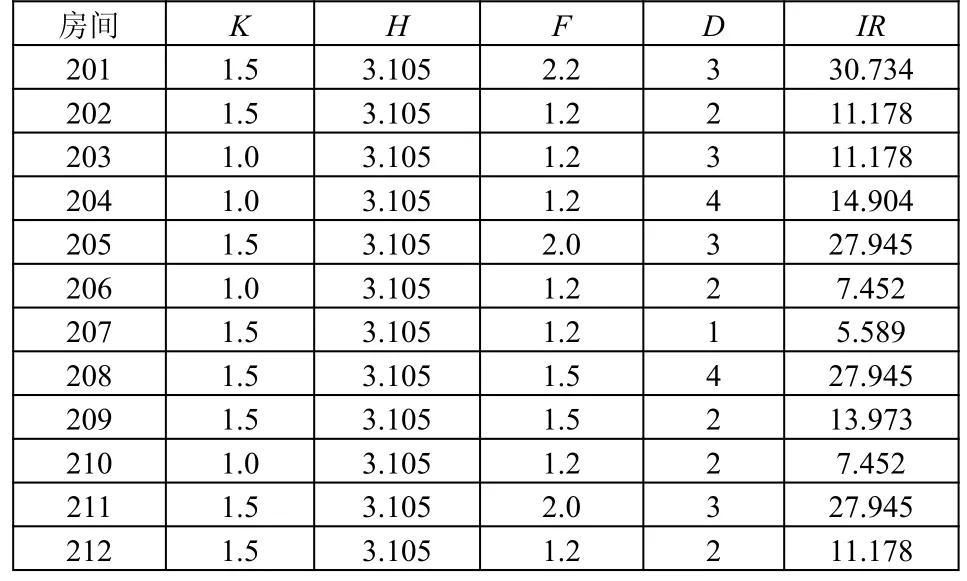
表5 建筑物内IR的计算结果

根据对建筑物危险度大和人员伤害大为参考因素，将危险关键部位定义为（3.603,26.019），划分建筑物内各个空间火灾危险区域。一级危险区域的房间：201,205；二级危险区域房间：208,211；其他房间为三级危险区域。

假定各个通道内的障碍物无影响，若此时206房间发生火灾，需要对该房间及周围房间（205、206、207）进行疏散。通过仿真获得的疏散路径如表6所示：

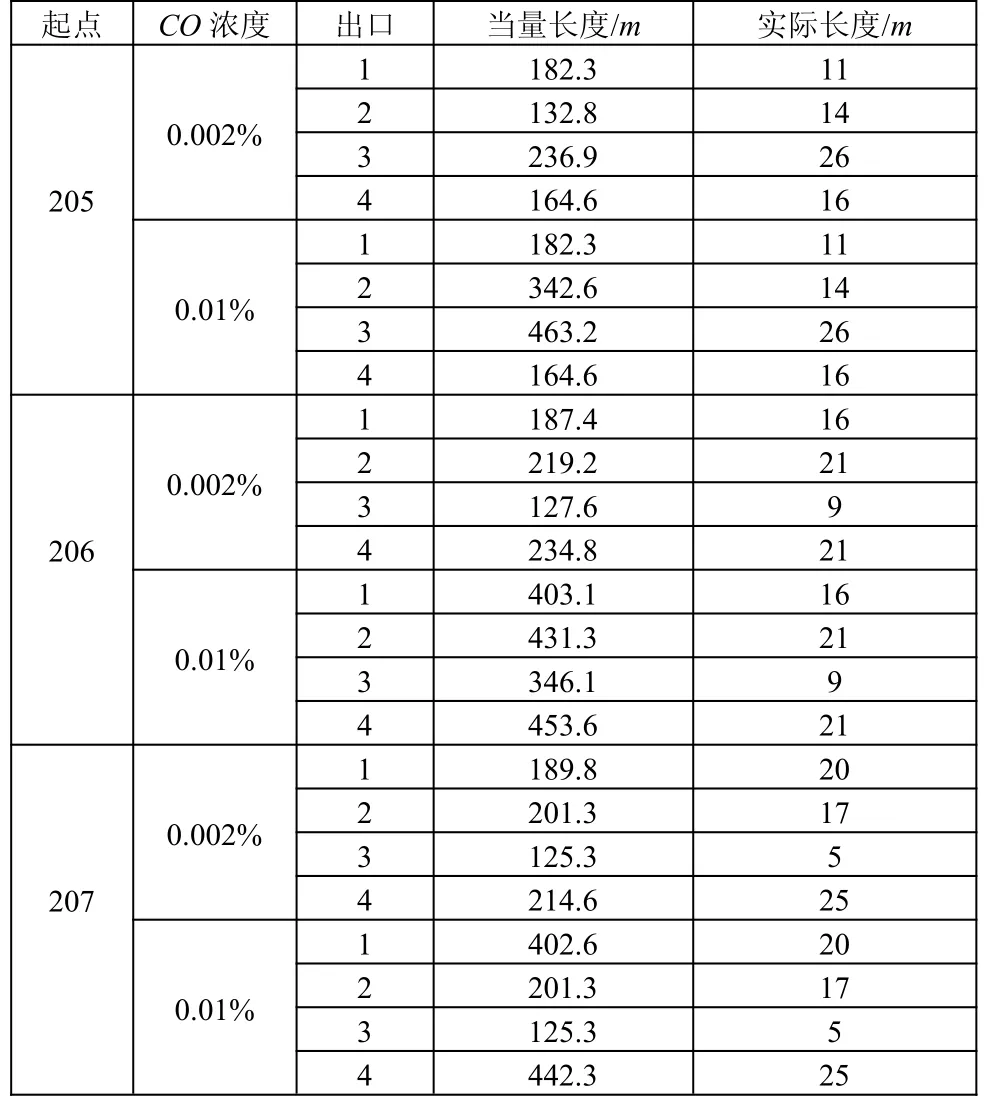
表6 节点205、206、207疏散路径

从上述表中可以看出，引入当量距离建立的模型获取的最优路径不是固定的，是随着有毒气体浓度的变化而变化的，同时可以看出实际距离最短的路径并不就是最优路径，这样更有利于人员的安全疏散。

5 总结

本文根据建筑物内部自身火灾风险及火灾产生有毒气体等因素对疏散路径的影响建立疏散路径选择模型，并具体分析确定各个因素的影响系数；同时采用二叉堆存储方式提高A*算法在大规模网络中的搜索效率。通过仿真实验验证了基于当量距离建立的疏散模型获得的最优路径更有利于人员快速、安全的疏散。同时本文方法还存在的不足和进一步待研究问题的分析，例如未考虑人员密度的影响等。

[1]夏之彬.大型建筑物火灾应急疏散避险系统设计[J].消防设备研究,2012(10).

[2]王丹.智能疏散指示系统的研究[D].安徽理工大学硕士学位论文,2012.

[3]孙茜茜,陆楠.求解最短路径问题的改进人工鱼群算法[J].信息技术,2014,1(9).

[4]朱淑敏.基于火灾区域和人员疏散复合模拟研究[D].中南大学硕士论文,2010.

[5]朱孔全.建筑内典型区域人员疏散特性及疏散策略研究[D].中国科学技术大学博士论文,2013.

[6]金曦,姜治宇,张雪等.重特大事故人员疏散算法设计及系统实现[J].东北大学学报,2013,34(10).

[7]李娜.基于动态网络流的舰船人员疏散方法研究[D].哈尔滨工程大学硕士学位论文,2011.

[8]杨立兵.建筑火灾人员疏散行为及优化研究[D].中南大学博士学位论文,2013.

[9]余为波,吴晓光,王涛等.基于最短路径算法的船舰通道逃逸路线研究[J].中国船舰研究,2008,3(2).

[10]王爱莎.高层建筑火灾时的人员安全疏散研究[D].安徽理工大学硕士学位论文,2013.

[11]谢旭阳,任爱珠,周心权.高层建筑火灾最佳疏散路线的确定[J].自然灾害学报,2003,12(3).

[12]张培红,王粟,黄晓燕.公共聚集场所疏散通道障碍物对人员疏散安全性的影响[J].沈阳建筑大学学报,2007,23(6).

[13]黄莺.公共建筑火灾风险评估及.安全管理方法研究[D].西安建筑科技大学博士学位论文,2009.

[14]陶亦然.基于古斯塔夫法的大型购物中心火灾风险评估[J].消防管理研究,2010,29,(3).

[15]赵伟.应用古斯塔夫法评估城中村火灾风险.[J].消防管理研究,2012,31,(3).

[16]张姣.大型地下商场火灾风险评估的研究[D].中国地质大学硕士学位论文,2013.

[17]周小静.基于改进A*算法的游戏地图寻径的研究.[D].西南大学硕士论文,2011.

Optimal Path Research of Building Intelligent Evacuation System

Hu Zhiguo,Jia Zhen,Kang Quanyu,Yang Junqiang
(School of Electrical Engineering and Automation,Henan Polytechnic University,Jiaozuo 454003,China)

To get the optimal evacuation path that can help people evacuate fast and safely when a fire occurs in a building,this paper sets up the evacuation route choice model based on the equivalent length according to the factors of the fire risk in the building and different development stage of the fire.It gets the optimal evacuation path fast with the improved A*algorithm.After the simulation experiments on a building of Zhengzhou,the results show that the actual distance of the shortest path is not the most optimal evacuation route,and according to the change of the development stage of the fire,the optimal path also makes corresponding changes which are beneficial to evacuate safely.

The Optimal Evacuation Path;Equivalent Length;A*Algorithm

TP391

A

1007-757X(2015)06-0022-04

2014.10.30）

胡治国（1977-），男，河南理工大学，副教授，博士，研究方向：质量和工业过程控制，焦作，454000

贾 珍（1990-），女，河南理工大学，硕士研究生，研究方向：控制工程，焦作，454000

康全玉（1964-），男，河南理工大学，教授，博士，研究方向：矿工程的教学与科研工作，焦作，454000

杨俊强（1987-），男，河南理工大学，硕士研究生，研究方向：电力系统谐波分析，焦作，454000