灾变事件下高速公路管理单元的行程时间研究*
2015-04-21阎莹王晓飞
阎莹 王晓飞
(1.长安大学 汽车运输安全保障技术交通行业重点实验室, 陕西 西安 710064;2.华南理工大学 土木与交通学院, 广东 广州 510640)
灾变事件下高速公路管理单元的行程时间研究*
阎莹1王晓飞2†
(1.长安大学 汽车运输安全保障技术交通行业重点实验室, 陕西 西安 710064;2.华南理工大学 土木与交通学院, 广东 广州 510640)
为有效服务于灾变事件下高速公路通道路网的路径诱导和控制管理,提出了路网中管理单元的划分方法;针对未发生灾变事件的管理单元,考虑管理单元长度、平均车速以及实时交通密度的影响,建立行程时间特性函数;结合发生灾变事件时管理单元的排队-消散特征,利用流量、密度关系模型确定事件持续时间和消散时刻,构建基于波动理论的事发管理单元行程时间模型;以实时安全可靠度作为路阻函数对模型进行了修正,最后通过实例验证了计算模型的有效性.
灾变事件;高速公路通道路网;管理单元;行程时间;波动分析
高速公路作为承载交通流量的快速通道,其行程时间可靠性是影响出行者出行选择最重要的因素之一.行程时间的变化对于制定相应的交通控制管理策略、评估路网服务水平等级以及选择驾驶路线都有着重要意义.然而,高速公路运行状态极易受到一些随机因素影响,导致行程时间的波动性加剧.如何采用有效的方法对当前高速公路路段的行程时间信息进行准确估计与预测已引起国内外学者广泛关注.
1991年,Asakura等[1]提出行程时间可靠性概念用于分析出行者出行行为及出行需求.1997年,Bell等[2]提出考虑交通需求变化,基于灵敏度的行程时间估计方法.2004年,Wakabayashi[3]建立了多因素影响下路段行程时间可靠性模型.2008年,Van Lint等[4]对高速公路行程时间可靠性的指标进行了研究.2010 年,Steven 等[5]研究了不同交通量和天气条件下高速公路行程时间的可变性和可靠性.随着行程时间研究的深入,考虑的因素以及建立的模型越来越完善,应用也越来越广泛.国内已初步开展了灾变事件(主要是恶劣天气)对高速公路行程时间影响的研究,虽取得了一些研究成果[6- 11],但由于我国高速公路交通情况比较复杂、特殊,驾驶行为与交通设施、管理方法、控制系统的不同均可能导致某些行程时间确定方法与国外高速公路存在着较大差异,造成实际应用中存在较大偏差.
鉴于此,文中在对高速公路通道路网管理单元划分的基础上,充分考虑灾变事件对于管理单元行程时间的影响,基于波动理论建立了未发生和发生灾变事件两种不同交通状况下行程时间的确定方法,并以实时安全可靠度作为路阻函数对模型进行了修正,以期为高速公路路网运营安全管理和应急处置决策的制定提供依据.
1 通道路网中管理单元的划分
灾变事件是诱发高速公路拥挤和运营安全性下降的重要原因,包括灾害性天气、交通事故及不安全驾驶行为等[12].当高速公路上发生灾变事件时,将直接影响道路的运营安全,随之在路网范围内扩大,进而使得路段通行能力及服务水平降低,导致出现拥堵及排队等不良交通现象.
解决此类问题的首要步骤是对高速公路路网进行管理单元划分.文中所研究的管理单元划分是为了更好地了解路网管理系统的设施特性、交通特性、安全特性、通行能力特性等,服务于行程时间这一动态属性的计算,以便能在交通管理中根据行程时间这一路阻函数制定诱导对策.管理单元是决策分析的对象,管理单元划分在很大程度上决定了系统决策分析结果的正确与否及其在实际工作中的实用程度[13].目前,高速公路通道路网管理单元划分尚无统一完善的原则和科学简洁的数据模型[14- 15].城市道路的划分方法,采用以路名和交叉道路来划分管理单元的固定分段,值得借鉴.但是,高速公路本身交叉较少,采用立交控制点作为分段点所获得的管理单元往往很长,不便于某些点位的安全性问题分析,而且单元内路段本身有些可组织交通的设施也被忽略,造成资源浪费.此外,管理单元的划分并非越细越好,而是因系统目标而异.图1简要说明了管理单元划分与系统目标的关系.

图1 单元划分与系统目标关系图
图1将系统目标划分为3个层次,第1、2层次管理单元目标较为宏观,以制定管理单元交通控制与管理对策、决策为主;第3层次则主要服务于微观的管理单元属性分析.对于高速公路通道路网而言,应保证管理单元内与系统决策有关的主要属性的一致性,即将主要属性变化点作为分段结点.例如,高速公路不同交叉口之间,交通量等动态属性一般不会发生变化,因此只需控制其沿行车方向上的离散性即可.由于行程时间的研究主要服务于灾变事件下高速公路路径诱导、路段交通控制与管理等,因此根据系统目标并结合图1,提出管理单元划分方法及步骤如下.
步骤1 首先将路网按等级、路名、行车方向的不同划分成不同路段,并确定各路段起终点;
步骤2 根据高速公路上下行方向,按照高速公路起终点、出入口、立交、收费站、服务区、隧道起终点等路网节点位置划分路段,确定管理单元.
2 管理单元行程时间计算
高速公路路段行程时间是指一辆车在某一时间段内通过路段需要花费的期望时间,是进行交通诱导管理对策及决策的重要依据[16].在路径选择中,路阻函数可反映行程时间、经济成本、安全性等因素,其中行程时间是最重要的参数,因为出行者希望能选择行程时间较短的路线绕行,而且所有的其他因素都与行程时间密切相关,且呈现出与行程时间相同的变化趋势.
高速公路网行程时间受众多因素影响,包括驾驶员、车辆类型等非线性行为,天气变化等环境因素,交通事故、交通管制等人为因素等.以下提出不同事件条件下的行程时间确定方法.
2.1 未发生灾变事件时行程时间的计算
当路段管理单元未发生灾变事件时,单元长度、平均车速、实时交通密度等均会影响行程时间,此时管理路段单元i的行程时间可以表示为

(1)
式中,c(i,t)为t时刻管理单元i的行程时间,Li为管理单元i的长度,v(i,t)为管理单元i在t时刻的车速.
根据Greenshields速度与密度函数[17]:

(2)
(3)
式中,k(i,t)为管理单元i、t时刻的车流密度,vf为自由流速度,kj为阻塞密度.
2.2 发生灾变事件下行程时间的计算
2.2.1 基于波动理论的事发单元排队-消散过程分析
当某管理单元i发生灾变事件,则该事发单元行程时间t包括3个部分,如图2所示.

图2 事件发生时的行程时间示意图
根据交通流理论,当发生灾变事件后,事发点的通行能力降低,上游交通需求大于通行能力时,形成向后的“返回波”,如图3(a)所示.灾变事件排除后,发生 “启动波”,波尾还有车辆陆续到达,出现“返回波”和“启动波”同时并存的现象,二者均向后移动.ti1,1为车辆从上游结点至排队y(t)队尾的行驶时间,ti1,2为在排队y(t)中的拥堵时间,ti2为事发点瓶颈段下游行驶时间,则ti1=ti1,1+ti1,2,很显然此时行程时间t=ti1+ti2.
假定在本车道上游交通流密度为kr,交通需求流量为qr.根据灾变事件等级属性为n,则瓶颈点的通行能力下降为Cn.交通流密度相应地上升为k2,灾变事件持续时间为ta,即从灾变事件产生到交通流状态恢复正常所需的时间,包括:第1阶段,事件产生到系统检测并确认;第2阶段,确认事件到救援车辆到达事发现场;第3阶段,救援车辆到达到离开;第4阶段,交通流恢复阶段,即从事件清除到排队完全消散.记检测阶段至清除阶段时间为te,可以看出,te与上游车辆排队长度行驶及等待时间ti1密切相关.
1)事件消散的波动分析
在事件检测至清除时间te内,当qr≤Cn时,k1=k2=k4,路段通常不会产生交通拥堵,如图3(b)所示.而当qr>Cn时,通行能力不能满足交通需求,交通拥挤随之产生,如图3(c)所示.
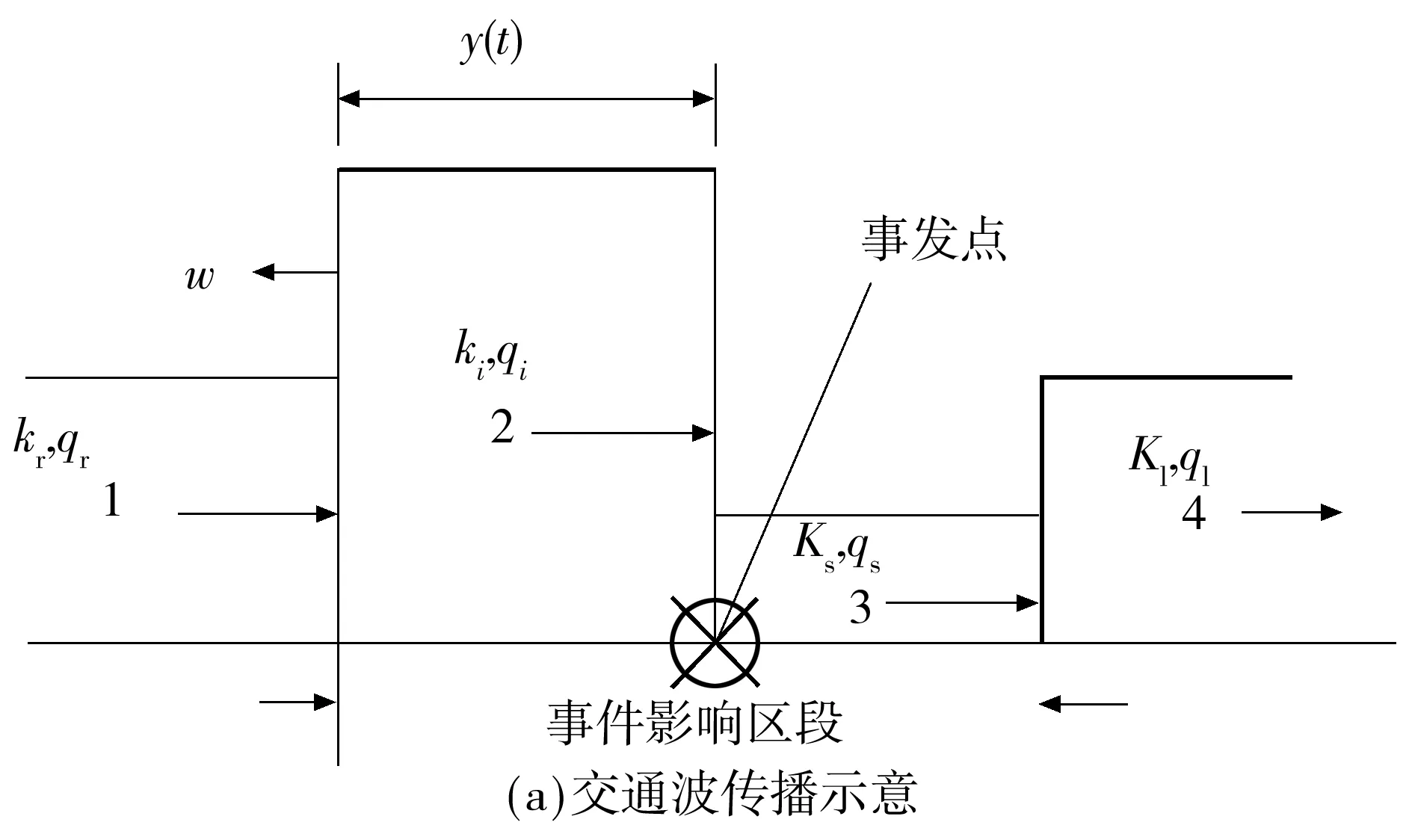


图3 事发点交通波示意图
图4是车流阻塞—消散过程的波形时距图,图中y、t分别代表距离和时间.点O对应事发点,t=0对应事发时刻,当t=te时,表示事件清除完毕.FA段内发生拥堵,拥堵密度为ki,流率为qi;此时,假定A的上游车辆以平均流率qr到达,交通流密度保持kr;当灾变事件发生时,路段上车辆以qs、ks运行,事发点处车流达到最大通行能力,此时流量qs=Cn;经过一段时间,则事件发生路段彻底堵塞,qs=0,ks=kj.从事发点处开始绘制特性曲线,t=te时,点F的密度由ki很快变为km(最大通行能力对应的密度),这样特性曲线在B点呈扇形展开,如图4所示.
从图4可以看出,特性曲线沿边界把坐标平面划分成3个流量-密度状况截然不同的区域.特性曲线相交线即为交通波曲线OABCD,也就是拥堵车队队尾的轨迹,用y(t)表示车辆排队长度.
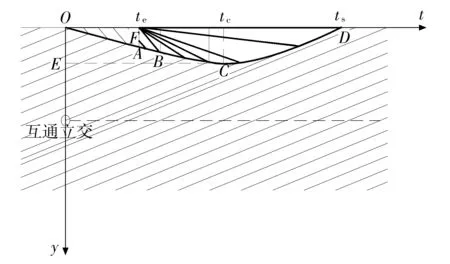
图4 车流阻塞-消散过程的波形时距
首先,在OF段产生的交通波相对于事发点向后传播至B点结束,B点代表最后一条由事发点发出的具有密度ki的特性曲线.在B点之后,由于区域FBD内呈扇形放射的特性曲线具有不同的密度,且交通波在向下游传播的过程中密度不断变化,而从互通立交向事发点传播的交通波密度恒为kr,因此BCD呈非线性变化且以变化的速度传播.
当车辆进入上游互通立交并逐渐行驶到事发点附近时,若拥堵尚未结束,则其离开事发点的时间为ti1=ts;若拥堵已经结束,车辆则不受拥堵干扰,行程时间则可表示为上游流量的函数.
2)事件消散时刻的计算解析
为获得曲线OABCD各段模型以及点B、C、D坐标的解析结果,假定流量-密度模型为如图3所示的GREENSHIELD模型.OB为事件发生后返回波的轨迹,则波速为
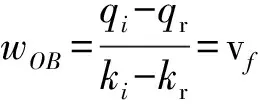
(4)


由上两式可得
(5)
又

因此
(6)
设kR表示曲线段BCD上任意一点的交通流密度,则该点的波速为

(7)
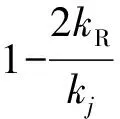
(8)
求解微分方程可得
yBCD(t)=(-h(ki)+h(kr))·
[(t-te)(tB-te)]1/2-h(kr)(t-te)
(9)
令yBCD(t)=0,灾变事件消散时刻ts为

(10)
式中,kr为事件发生点上游附近的交通流密度,可由检测器检测得到,当qr>Cn时,
(11)
式中,C为事发路段实际通行能力,则事件持续时间为
(12)
2.2.2 行程时间计算模型的建立

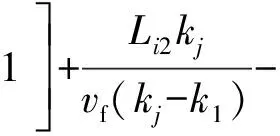
(13)
式中,ki为管理单元i的车流密度,kj为阻塞密度,te为事件清除时间,vf为自由流车速,kr为管理单元i上游车流密度,Li2为事发点与管理单元i终点之间的距离,t0为事件发生时间,t为车辆进入管理单元i的时间,其他参数含义同前.
需要指出的是te为灾变事件检测、响应和清除3个阶段的总时间,其中事件类型、事件严重程度、各高速公路管理中心的联动管理水平等因素都会影响事件清除时间.目前,事件清除时间的统计方法主要有线性回归法、方差分析法、决策树法、非参数回归法、hazard duration method、模糊逻辑法等,在此不再赘述.
2.3 考虑运营安全的行程时间模型修正
主线高速公路管理单元发生灾变事件后,事发单元的通行能力和运营安全性都会受到影响.即使事发单元采取了相应的应急措施,倘若上游单元实时交通量较大,且没有任何限流、诱导对策,驾驶员盲目前进的后果将导致事发单元拥堵向上游扩展.此时,交通管理者可提供两种交通诱导建议策略:一是选择在高速公路上等待或者缓慢通过事发单元;二是提供可行路径,即从事发点前方某出口绕开事发单元,回到事发点后某一节点.针对所有诱导方案的起终点,应在满足一定安全要求和行程时间要求下,保证有足够通行能力来疏导上游交通需求,这样才能有效降低诱导路线所包含的管理单元以及整个路网的运行风险.因此,在确定行程时间、选择诱导路径时,为了同时满足管理单元实时安全可靠度的需求,可对路阻函数做出如下修正:

(14)
式中,SD(i,t)为管理单元i在t时刻的安全可靠度;Sc为管理单元允许的最小安全可靠度.
则管理单元i发生灾变事件条件下,路段上游管理单元(i-k)行驶到单元i终点的行程时间计算公式可表示为


(15)
3 实例分析
如图5所示,以0- 1- 2- 3- 4构建主线的高速公路通道路网,其中各个管理单元的道路设施类型为普通路段,表1为各管理单元的静态属性值.表2为各管理单元的实时动态属性值.检测到各级灾变事件位置为结点3- 4的中点,假定:一、二、三、四级事件的清除时间分别为10、20、30、40min.

图5 计算实例
表1 管理单元静态属性值
Table 1 Static attribute value of management unit

属性取值属性取值属性取值道路类型普通路段防护设施很好(90)/一般(60)车道数6/2车道运行车速差/(km·h-1)11/151)防眩设施很好(90)/一般(60)设计车速/(km·h-1)120/80路面综合指标/分90/70视线诱导很好(90)/一般(60)阻塞密度/(pcu·km-1)75视距/m500/150标志标线很好(90)/一般(60)车道宽度/m3.75沿线景观优劣很好(90)/一般(60)监控很好(90)/一般(60)侧向净空/m1长度见图4信息发布很好(90)/一般(60)车辆检测器个数2公路等级见图4预警系统很好(90)/一般(60)
1)取值依次为高速公路静态属性值/二级公路静态属性值,余同.
当未发生灾变事件时,行程时间可根据式(5)进行计算,表3为行程时间计算结果.以管理单元1(起点为0,终点为1)为例,首先查找表1和表2中管理单元的静态、动态属性值,管理单元位于六车道高速公路上,长度为20 km,阻塞密度kj为75 pcu/km,自由流车速vf为120 km/h,车流密度ki为36 pcu/km,
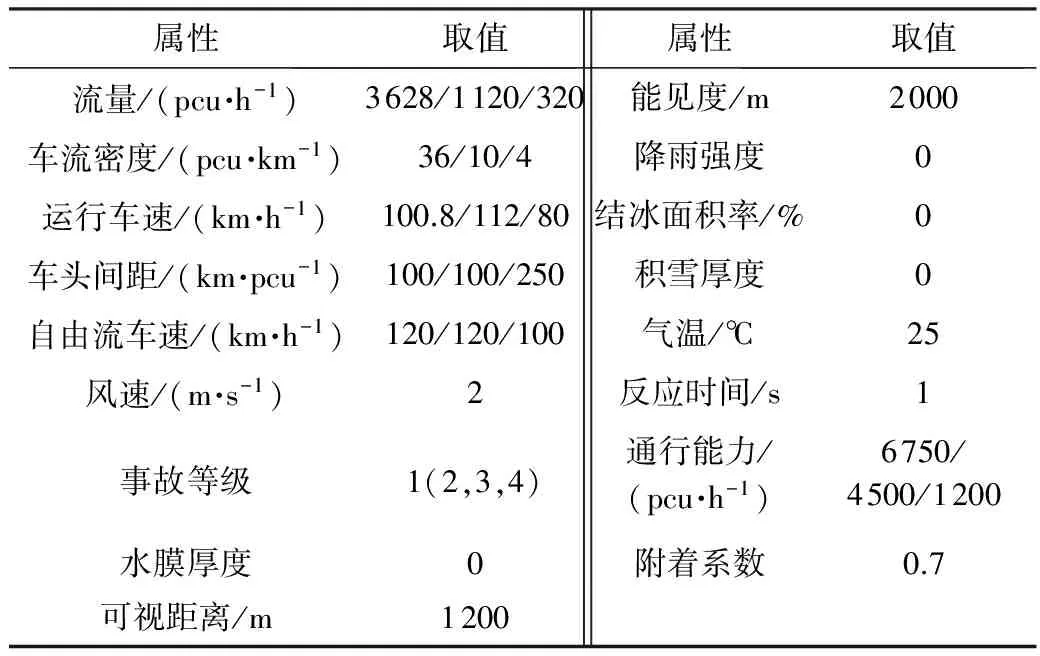
表2 管理单元动态属性值1)
1)取值依次为六车道高速公路动态属性值、四车道高速公路动态属性值、二级公路动态属性值.

表3 未发生灾变事件情形下各管理单元行程时间
然后将上述属性值代入式(5)可得:

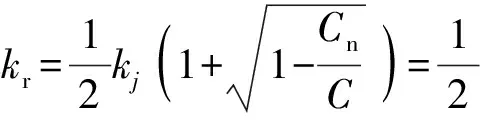
同理可计算得到的管理单元4发生灾变事件时主线上游各结点到结点4的行程时间,结果见表4.
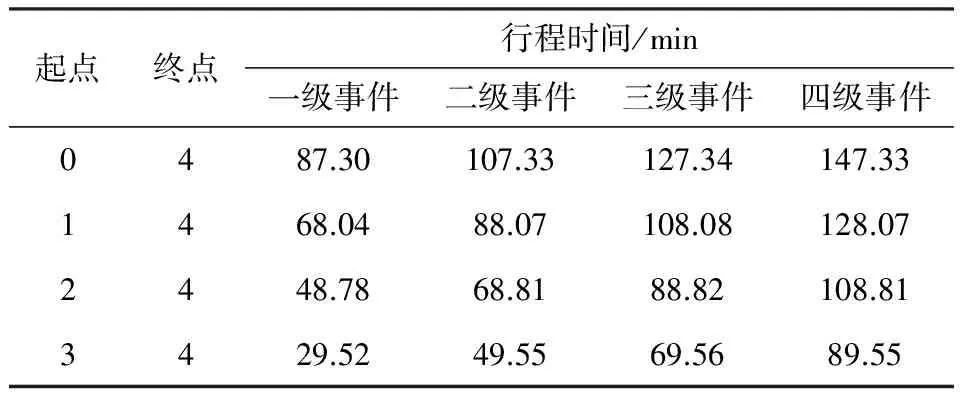
表4 管理单元4发生灾变事件时各结点间的行程时间
4 结语
实时估计路段行程时间并相对准确地预测灾变事件下将来某一时刻路段的行程时间,对于提高交通管理水平、制定交通出行决策具有重要的现实意义.
文中结合车辆在高速公路通道路网行驶特点,按照路名、等级、行车方向以及路网结点位置等因素划分路网管理单元;首先建立在车辆速度和交通流密度影响下路网中未发生灾变事件管理单元行程时间的计算模型;然后通过分析灾变事件的排队、消散过程,得到事件消散的解析解以及事件持续时间的计算方法,构建基于波动理论的发生灾变事件的行程时间计算模型;同时考虑运营安全的需求,对模型进行了修正,并用实例对模型进行了验证.研究成果对高速公路车辆行程时间预测的工程实践提供了很好的理论依据和合理的解决方案.
[1] Asakura Y,Kashiwadani M.Road network reliability caused by daily fluctuation of traffic flow [C]∥ Proceedings of the 19th PTRC Summer Annual Meeting.Brighton:University of Sussex,1991:73- 84.
[2] Bell M G H,Cassir C,Iida Y,et al.A sensitivity based approach to network reliability assessment [C]∥Procee-dings of 14th International Symposium on Transportation and Traffic Theory.Jerusalem:Elsevier,1999:283- 300.
[3] Wakabayashi H.Travel time reliability on expressway network under uncertain environment of snowfall and traffic regulation [J].Faculty of Urban Science,2004,3(3):156- 160.
[4] Van lint J W C,Van Zuylen H J.Monitoring and predicting freeway travel time reliability using width and skew of the day-to-day travel time distribution [J].Transportation Research Record,2005,1917:54- 62.
[5] Steven I Chien,Kiran K Kolluri.Evaluation of freeway travel time variability and reliability under adverse weather with transmit data [J].Journal of Civil Engineering and Architecture,2012,6(1):1- 11.
[6] 郭冠英,邹智军.道路交通拥挤时的车辆排队长度计算法 [J].中国公路学报,1998,11(3):92- 102. Guo Guan-ying,Zou Zhi-jun.Algorithm of vehicle queuing length under crowded road [J].China Journal of Highway and Transport,1998,11(3):92- 102.
[7] 刘海旭,卜雷,蒲云.随机路网的行程时间可靠性 [J].土木工程学报,2004,37(8):102- 105. Liu Hai-xu,Bu Lei,Pu Yun.Travel time reliability on stochastic road network [J].China Civil Engineering Journal,2004,37(8):102- 105.
[8] 侯立文,谭家美.信息条件下路段出行时间可靠性的计算 [J].上海交通大学学报,2006,40(6) :968- 972. Hou Li-wen,Tan Jia-mei.Computing the link travel time reliability with information provision [J].Journal of Shanghai Jiaotong University,2006,40(6):968- 972.
[9] 陈琨,于雷.基于对数正态和分布的路径行程时间可靠性模型 [J].北京交通大学学报,2009,33(3):35- 39. Chen Kun,Yu Lei.Route travel time reliability model based on lognormal sum distribution [J].Journal of Beijing Jiaotong University,2009,33(3):35- 39.
[10] 徐天东,孙立军,郝媛.城市快速路实时交通状态估计和行程时间预测 [J].同济大学学报:自然科学版,2008,36(10):1355- 1361. Xu Tian-dong,Sun Li-jun,Hao Yuan.Real-time traffic state estimation and travel time prediction on urban expressway [J].Journal of Tongji University:Natural Science,2008,36(10):1355- 1361.
[11] 吴炼,李旭宏,王婧,等.雾天高速公路网行程时间可靠性评价方法 [J].解放军理工大学学报:自然科学版,2010,11(2):233- 238. Wu Lian,Li Xu-hong,Wang Jing,et al.Reliability evaluation on travel time in freeway network under fog environment influence [J].Journal of PLA University of Science and Technology:Natural Science Edition,2010,11(2):233- 238.
[12] 杨庆芳,马明辉,梁士栋,等.基于收费数据的高速公路交通状态判别方法 [J].华南理工大学学报:自然科学版,2014,42(12):51- 57. Yang Qing-fang,Ma Ming-hui,Liang Shi-dong,et al.Freeway traffic state identification based on toll data [J].Journal of South China University of Technology:Natural Science Edition,2014,42(12):51- 57.
[13] 王晓飞,郭忠印.高速公路网管理单元的实时安全可靠度 [J].华南理工大学学报:自然科学版,2009,37(7):15- 20. Wang Xiao-fei,Guo Zhong-yin.Real-time safety reliability of management unit of freeway network [J].Journal of South China University of Technology:Natural Science Edition,2009,37(7):15- 20.
[14] 邵敏华,孙立军.公路管理单元动态划分技术与数据模型研究 [J].同济大学学报,2004,32(3):343- 347. Shao Min-hua,Sun Li-jun.Research on segmentation technique and data modeling in highway management system [J].Journal of Tongji University,2004,32(3):343- 347.
[15] 高建平,吕勇衡,张续光.高速公路施工期救援路线动态管理单元划分 [J].中国安全科学学报,2014,24(9):171- 176. Gao Jian-ping,Lü Yong-heng,Zhang Xu-guang.A dynamic segmentation division method for freeway construction project emergency rescuing [J].China Safety Science Journal,2014,24(9):171- 176.
[16] 夏创文.高速公路网运行监测若干关键技术研究 [D].广州:华南理工大学自动化科学与工程学院,2013.
[17] 熊志华,邵春福,马社强.基于模糊感知的道路网行程时间可靠性研究 [J].中国人民公安大学学报:自然科学版,2006(6):90- 93. Xiong Zhi-hua,Shao Chun-fu,Ma She-qiang.Study on travel time reliability of road network based on fuzzy perception [J].Journal of Chinese People’s Public Security University:Science and Technology,2006(6):90- 93.
Investigation into Travel Time of Management Unit of Expressway in Disastrous Events
YanYing1WangXiao-Fei2
(1 Key Laboratory of Automobile Transportation Safety Support Technology, Chang’an University, Xi’an 710064,Shaanxi, China;2.School of Civil Engineering and Transportation, South China University of Technology,Guangzhou 510640, Guangdong, China)
In order to effectively serve the route guidance and control management of the expressway corridor network in disastrous events, a method to divide the management unit of road networks is put forward. For the management unit with no disastrous events involved, a travel time characteristic function is established by taking into account the influences of the management unit length, the average speed and the real-time traffic density. By combining the queuing and dissipating characteristics of the management units involving disastrous events and by using the flow and density relationship model, the duration time and dissipation time of incidents are determined, and a travel time calculation model of incident management units is constructed based on the wave theory. Then, the proposed model is modified by taking the real-time safety reliability as a road resistance function. Finally, the effectiveness of the constructed model is verified by an example.
disastrous event; freeway corridor network; management unit; travel time; wave analysis
2015- 05- 07
国家自然科学基金资助项目(51308059,51408229);中国博士后科学基金资助项目(2014M552399);国家科技支撑计划项目(2014BAH23F01- 1);长安大学中央高校基本科研业务费专项资金资助项目(310822152007) Foundation items: Supported by the National Natural Science Foundation of China(51308059,51408229) ,the China Postdoctoral Science Foundation(2014M552399) and the National Key Technology Research and Development Program of the Ministry of Science and Technology of China(2014BAH23F01- 1)
阎莹(1981-),女,博士,副教授,主要从事交通安全研究.E-mail: yanying2199@chd.edu.cn
† 通信作者:王晓飞(1980-),女,博士,讲师,主要从事道路安全研究.E-mail: xiaofeiw@scut.edu.cn
1000- 565X(2015)12- 0099- 07
U 412.3
10.3969/j.issn.1000-565X.2015.12.014
