光纤电流传感器偏转角及线性双折射研究
2015-04-20马天兵李东
马天兵 李东
摘要:光纤电流传感器中由于光纤的弯曲以及自身特性,会同时存在线性双折射和法拉第效应,致使法拉第效应的偏转角无法被准确测量出来,这是造成光纤电流传感系统测量误差的一个重要因素。利用MATLAB模拟了线偏振光转化为圆偏振光和椭圆偏振光以及法拉第效应,并对法拉第效应中左右旋圆偏振光相位差设定了不同参数,利用MATLAB得出最终合成的线偏振光,观察其偏转角为所设左右旋圆偏振光相位差的1/2,之后进行了理论推导,验证了上述结论,为后续的线性双折射补偿研究奠定良好的基础。
关键词:光纤电流传感器; 线性双折射; 法拉第效应; 偏转角
中图分类号:TN253 文献标志码:A文章编号:1672-1098(2014)04-0056-05
光纤电流传感器是以法拉第效应为理论基础的一种电流测量装置[1-2],由于采用光纤传感技术,相对于传统的电磁式电流传感器,具有抗电磁干扰能力强,体积小,可靠性强等优点,有着广泛的应用前景,在被提出的近二十年中,一直广受关注,大量的资金以及人力被投入到这方面的研究当中。目前已有少量的这种传感器被投入到试运行当中,大规模的实用化仍然还有许多问题需要解决。
光纤电流传感系统中电流引起的法拉第效应与传感头中的线性双折射混杂在一起,导致法拉第效应所产生的法拉第偏转角无法被准确测量出来,这是影响其实用化的一个重要因素[3-4]。目前在这方面的研究也已出现了许多进展,如在传感光纤中加入大量圆双折射可以有效抑制线性双折射,以及对光纤环进行退火以消除线性双折射[5-6]。然而仍无法完全消除线性双折射对法拉第效应的影响。本文利用MATLAB对线性双折射和法拉第效应进行了模拟,有助于发现两者的区别,为系统的实用化设计和线性双折射与法拉第效应的分离提供一定的参考,且发现经过法拉第效应后所得的线偏振光偏转角为左右旋圆偏振光相位差的一半,并进行了理论推导。
1全光纤电流传感器基本原理
光纤电流传感器依据的理论基础是法拉第效应,即线偏振光通过位于磁场中的介质时,其偏振的角度会发生偏转,由光源发出的光经过起偏器形成线偏振光,进入45°熔接点分解为相互正交的X,Y线偏振光,分别经过λ/4波片,转换为左右旋圆偏振光,进入传感光纤,在电流产生的磁场环境中会发生法拉第效应,造成左右旋圆偏振光的光速不一致,产生相位差,经反射镜反射继续以全反射方式在光纤中传播,再次发生法拉第效应,由于法拉第效应的非互易性,左右旋圆偏振光产生的相位差不会抵消,会进行累积,最后再次经过λ/4波片会转变为两道线偏振光,两正交偏振光所合成的线偏振光相对于初始的线偏振光,其偏振角度会发生偏转,偏转的角度与产生磁场的电流以及材料的菲尔德常数有关[7]。通过测量输出偏振光的偏转角度从而得到所测电流大小,其偏振面偏转的角度公式为
θ=VBd (1)
式中:θ为偏转角,V为费尔德常数,B为电流产生的磁场,d为偏振光通过磁场中的介质长度。
2线性双折射
由光源产生一束自然光,经起偏器形成线偏振光进入传感光纤,以全反射方式在光纤中传输,当光纤中局部处由于受到应力或弯曲因素影响,光纤此处由各向同性特性转变为各向异性特性,形成单光轴[8],介质对于x,y方向偏振光的折射率以及传播速度不同,造成此正交偏振光产生相位差,就会发生线性双折射。假设x、y方向折射率分别为nx和ny,真空中的原始波长为λ,则x方向的介质波长为λ/nx,y方向介质波长为λ/ny,发生双折射长度为L,则x偏振光在介质L长度中发生了ω0角度传播
ω0=2πLnxλ (2)
同时间点y偏振光在光纤中传输距离为
Ly=ω0×λny=Lnxny (3)
x,y在x偏振光传输完L距离时间点具有ΔL位移差
ΔL=L-Lnxny=Lny-nxny (4)
相对相位差δ
δ=2πΔLλny=2πLny-nxny×nyλ=
2πL(ny-nx)λ (5)
用以下方程对发生线性双折射后所得线性偏振光进行描述
E=Excos(ωt+δx)
Eycos(ωt+δy) (6)
我们设置光纤中形成的光轴方向与入射线偏振光的偏振方向成45°,则
Ex=Ey (7)
且两束正交的偏振光由其折射率差在传输L距离后产生的相位差为π/2,(2n+1)π/2时,即
δ=δx-δy=2n+12π (8)
其最终会形成圆偏振光,利用MATLAB软件进行编程,设置Ex=Ey,两正交偏振光相位差为π/2,所得结果如图1所示。(1) 传播示意图(2) 末端轨迹图
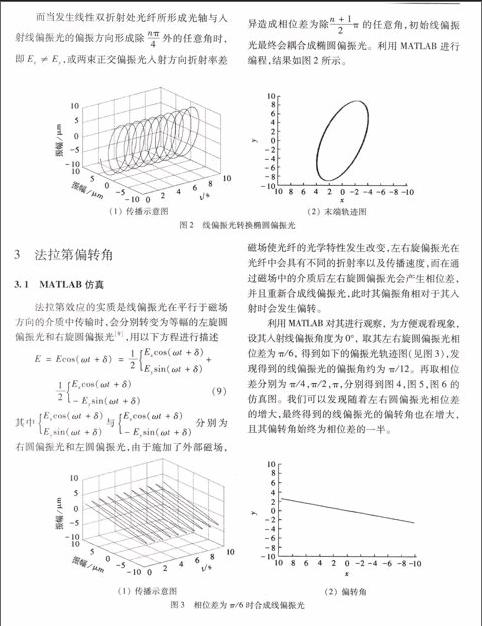
图1线偏振光转换圆偏振光而当发生线性双折射处光纤所形成光轴与入射线偏振光的偏振方向形成除nπ4外的任意角时,即Ex≠Ey,或两束正交偏振光入射方向折射率差异造成相位差为除n+12π的任意角,初始线偏振光最终会耦合成椭圆偏振光。利用MATLAB进行编程,结果如图2所示。
(1) 传播示意图 (2) 末端轨迹图
图2线偏振光转换椭圆偏振光
3法拉第偏转角
31MATLAB仿真
法拉第效应的实质是线偏振光在平行于磁场方向的介质中传输时,会分别转变为等幅的左旋圆偏振光和右旋圆偏振光[9],用以下方程进行描述
E=Ecos(ωt+δ)=12Excos(ωt+δ)
Eysin(ωt+δ)+
12Excos(ωt+δ)
-Eysin(ωt+δ) (9)
其中Excos(ωt+δ)
Eysin(ωt+δ)与Excos(ωt+δ)endprint
-Eysin(ωt+δ)分别为右圆偏振光和左圆偏振光,由于施加了外部磁场,磁场使光纤的光学特性发生改变,左右旋偏振光在光纤中会具有不同的折射率以及传播速度,而在通过磁场中的介质后左右旋圆偏振光会产生相位差,并且重新合成线偏振光,此时其偏振角相对于其入射时会发生偏转。
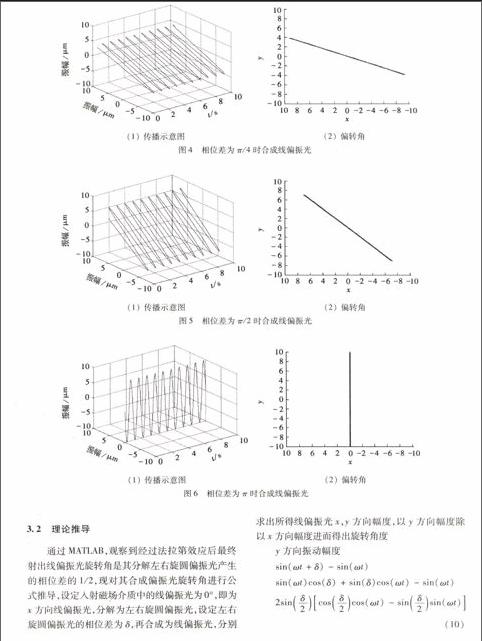
利用MATLAB对其进行观察, 为方便观看现象, 设其入射线偏振角度为0°, 取其左右旋圆偏振光相位差为π/6, 得到如下的偏振光轨迹图(见图3),发现得到的线偏振光的偏振角约为π/12。再取相位差分别为π/4,π/2,π,分别得到图4,图5,图6的仿真图。我们可以发现随着左右圆偏振光相位差的增大,最终得到的线偏振光的偏转角也在增大,且其偏转角始终为相位差的一半。(1) 传播示意图 (2) 偏转角
图3相位差为π/6时合成线偏振光(1) 传播示意图(2) 偏转角
图4相位差为π/4时合成线偏振光
(1) 传播示意图(2) 偏转角
图5相位差为π/2时合成线偏振光
(1) 传播示意图(2) 偏转角
图6相位差为π时合成线偏振光
32理论推导
通过MATLAB,观察到经过法拉第效应后最终射出线偏振光旋转角是其分解左右旋圆偏振光产生的相位差的1/2,现对其合成偏振光旋转角进行公式推导,设定入射磁场介质中的线偏振光为0°,即为x方向线偏振光,分解为左右旋圆偏振光,设定左右旋圆偏振光的相位差为δ,再合成为线偏振光,分别求出所得线偏振光x,y方向幅度,以y方向幅度除以x方向幅度进而得出旋转角度
y方向振动幅度
sin(ωt+δ)-sin(ωt)
sin(ωt)cos(δ)+sin(δ)cos(ωt)-sin(ωt)
2sinδ2cosδ2cos(ωt)-sinδ2sin(ωt)
(10)
x方向振动幅度
cos(ωt+δ)+cos(ωt)
cos(ωt)cos(δ)-sin(δ)sin(ωt)+cos(ωt)
2cosδ2cosδ2cos(ωt)-sinδ2sin(ωt)
(11)
以y偏振光幅度除以x方向偏振光幅度得出其偏转角,结果显示其偏转角为相位差的一半
2sinδ2cosδ2cos(ωt)-sinδ2sin(ωt)2cosδ2cosδ2cos(ωt)-sinδ2sin(ωt)
=tanδ2 (12)
4结论
对各向异性介质中两垂直偏振光相位差和对光纤电流传感器中的线性双折射以及法拉第效应进行了理论推导,设置了合理的参数,利用MATLAB对二者进行了仿真,仿真结果表明,线偏振光的正交线性偏振光幅值相等,相位差为π/2时,合成光为圆偏振光,当正交偏振模幅值不等或相位差不为π/2时,合成光为椭圆偏振光。并对法拉第效应线偏振光转为左右旋圆偏振光,设定相位差,分别进行了MATLAB模拟和理论推导,结果显示,法拉第效应后最终合成线偏振光偏转角为左右旋圆偏振光相位差的1/2,为后续的线性双折射补偿研究奠定良好的基础。
参考文献:
[1]KLAUS BOHNERT,PHILIPPE GABUS,JRGEN NEHRING.Fiber-optic current sensor for electro winning of metals[J]. Journal of Lightwave Technology, 2007,25(11): 3 602-3 609.
[2]鲁怀敏,蔡李花,方海峰,等.光纤电流传感系统影响因素分析[J].电子技术应用,2013,6(39):81-84.
[3]康崇,吕文磊.光学电流互感器中线性双折射与法拉第效应的分离检测[J].光学学报,2008(1):163-168.
[4]CEASE T W.Johnston P.A magneto-optic current transducer[J]. IEEE Trans on Ptor Del,1990,15(2):548-553.
[5]王景飞,梁京伟.反射式Sagnac干涉光纤电流互感器的传感头误差研究[J].光学与光电技术,2011(2):23-26.
[6]姜中英,张春熹.线性双折射对光纤电流互感器影响的研究[J].光学技术,2006,8(32):218-223.
[7]廖延彪.偏振光学[M].北京:科学出版社,2003:263-284.
[8]王伟,刘晓隆.光纤主轴方位角对光纤电流传感器的影响[J].中国激光,2013,1(40):231-236.
[9]郑勇林,郑瑞伦.磁性颗粒膜法拉第转角的研究[J].光学学报,2005,25(8):1 126-1 130.
(责任编辑:李丽)endprint