几种GPS高程拟合方法的分析与比较
2015-04-20李和旺
李和旺
摘 要:文章论述了几种常用的GPS高程拟合的方法,并在MATLAB中编制了相应的程序,建立了相应的GPS高程拟合模型,并通过实例数据进行建模分析,对比各方法的拟合结果的精度高低,得出了一些有益结论。
关键词:GPS;高程拟合;高程异常
1 概述
GPS高程测量具有劳动强度小、工作效率高、高程误差不累积等优点,但测得的高程不能直接用于生产实践中,对于GPS高程应用的不便性,国内外学者给予了普遍的关注。GPS高程转换是GPS应用研究领域的一个难点问题,也是GPS应用研究的热点问题。为了提高GPS高程转换的精度,国内外许多学者在GPS高程转换方法上进行了深入的研究,提出了很多种拟合方法[1-2],以便使GPS高程能够更广泛的应用到测量领域,充分发挥GPS高程测量的优越性。
文章主要探讨多项式曲线拟合法、样条曲线拟合、平面函数拟合法、二次曲面拟合法、多面函数法等方法[3]在GPS高程拟合中的运用,并通过实例数据进行分析比较,对比各方法的精度高低,得出了一些有益结论。
2 GPS高程拟合方法
2.1 多项式曲线拟合
若将坐标系转换成与测线x方向重合,与测线y方向垂直,则设高程异常值 和坐标x间存在下列函数关系:
(1)
已知点的高程异常和拟合得到的高程异常之差: ;
根据最小二乘原理,在?撞Ri2=min条件下求解各参数ai,然后利用(1)式求出各点的高程异常 ,从而求出各点的正常高。
2.2 二次曲面拟合法
二次曲面拟合法的数学模型为:
(2)
式中,x,y分别为点的纵、横坐标;a0,a1…a5为拟合系数。
由(2)式可知,二次曲面方程有6个待定系数a0,a1…a5,至少需要6个已知点才能进行计算。若已知点的个数为6个,可求出系数a0,a1…a5;若已知点的个数大于6个,系数a0,a1…a5由已知点通过最小二乘原理VTPV=min求得。
假设已知点点数为n,由(2)式可列误差方程:
(3)
表示成总误差方程形式:
V=BX-L (4)
式中,V=[v1,v2…vn]T; ;
X=[a0,a1,a2,a3,a4,a5]T;L=[?孜1,?孜2,…,?孜n]T。
由最小二乘原理VTPV=min,得到解为:
X=(BTB)-1BTL (5)
式中,V为改正数向量;L为高程异常值向量;X为拟合系数向量;B为系数矩阵。由此即可获得似大地水准面二次曲面拟合模型。
求得a0,a1,…a5后,即可根据点位的平面坐标利用(2)式子计算出待求点的高程异常 ,再利用GPS观测的大地高减去求出的高程异常 得到正常高[5]。
3 GPS高程拟合的精度评定
对拟合后的结果要进行精度评定,鉴于样本中既有拟合点又有检核点,一般采用内符合精度指标?滋1和外符合精度指标?滋2來评价拟合结果的好坏。
(6)
(7)
其中,v1为拟合高程异常的残差,n1为拟合计算点的个数,v2为拟合外推高程异常的残差,n2为拟合外推计算点的个数。内、外符合精度越小,表明拟合和预测的精度越高;反之,则说明拟合和预测的精度越差。
4 算例分析
某沿江地形平缓区域的GPS控制网共有无粗差且精度相同的水准点17个,平均边长约1km,区域面积约10km2,按国家GPS网B级要求施测,采用二等水准联测各GPS点,即:17点每个点都获取了平面位置和高程异常[7]。
为了消除点位分布因素的影响,选择均匀分布在整个测区内的8个点作为拟合点,剩下的9个点作为检核样本点。
用matlab编程建立模型,采用多项式拟合、三次样条曲线拟合、平面拟合、二次曲面拟合、多面函数拟合法进行GPS高程拟合,拟合结果见表1。
表1 几种拟合方法的结果比较
由表1可以看出,多面函数拟合的精度为2.0mm,二次曲面拟合的精度是1.8mm,这两种方法的精度都很高,平面拟合的内、外符合精度分别为2.4mm和4.1mm,其拟合精度也较高,三次样条曲线的的精度较差,多项式拟合的拟合精度稍高。
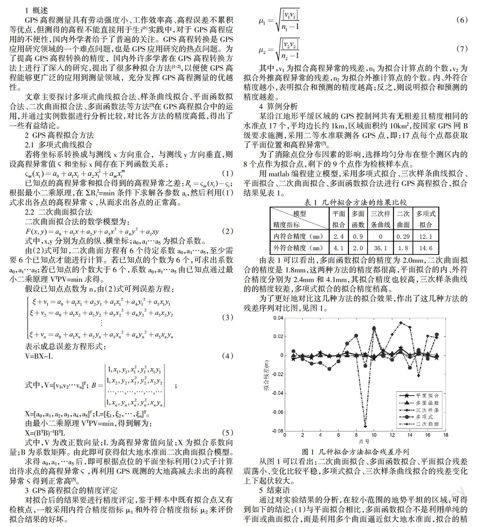
为了更好地对比这几种方法的拟合效果,作出了这几种方法的残差序列对比图,见图1。
图1 几种拟合方法拟合残差序列
从图1可以看出:二次曲面拟合、多面函数拟合、平面拟合残差震荡小、变化比较平稳,多项式拟合、三次样条曲线拟合的残差变化上下起伏较大。
5 结束语
通过对实验结果的分析,在较小范围的地势平坦的区域,可得到如下的结论:(1)与平面拟合相比,多面函数拟合不是利用单纯的平面或曲面拟合,而是利用多个曲面逼近似大地水准面,拟合的精度较高。(2)平面拟合、二次曲面拟合、多面函数拟合都比三次样条曲线拟合的精度高,是因为测区不是呈线状分布的,还有三次样条曲线拟合区域似大地水准面只考虑一个方向。(3)平面拟合、二次曲面拟合、多面函数拟合都比多项式拟合精度高。因为多项式拟合适用于线状分布的区域,而试验一中区域是呈面状分布的。
参考文献
[1]王旭,刘文生.GPS高程拟合方法的研究[J].测绘科学,2010,35:28-30.
[2]杨江波,李为乐,余代俊,等.GPS高程拟合方法的实验研究[J].测绘科学,2009,34(3):54-57.
[3]乔仰文,等.GPS高程转换的若干问题的研究[J].测绘通报,1999(11):17-19.
[4]胡永刚,武文波,刘利君.GPS水准高程拟合模型在线状工程中的研究及应用[J].测绘科学,2009,34(4):203-205.
[5]高原,张恒 ,赵春江.多项式曲面模型在GPS高程拟合中的应用[J].测绘科学,2011,36(5):179-181.
[6]Hardy RL.The application of multi quadraic equations and point mass anomaly models to crustal movement studies[J].NOAA Technical Report NOS,1978,76(11).
[7]胡伍生,高成发.GPS测量原理及其应用[M].北京:人民交通出版社,2004.