基于谱组合的GRACE/GOCE重力场模型融合处理

2015-04-20刘晓刚欧阳明达李迎春

测绘科学与工程 2015年4期

刘晓刚，肖云，欧阳明达，李迎春

1. 西安测绘研究所，陕西西安，710054；2. 地理信息工程国家重点实验室，陕西西安，710054；3. 信息工程大学地理空间信息学院，河南郑州，450001；4. 测绘信息技术总站，陕西西安，710054

刘晓刚1,2，肖云1,2，欧阳明达3,4，李迎春1,2

本文讨论了谱组合的基本原理，给出了多种类型重力测量数据融合处理的谱权及谱组合的通用表达式；根据位系数的误差阶方差，推导了由GRACE和GOCE数据构建地球重力场模型的谱组合公式及对应谱权的具体形式；采用谱组合法，由tongji-grace01和go-cons-gcf-2-tim-r5模型构建了谱组合模型grace+goce，并与go-cons-gcf-2-dir-r5模型的精度进行比较。试验结果表明，GRACE数据可以显著改善GOCE数据模型在中长波部分的精度，从而提高谱组合模型的整体精度；与单一卫星数据解算的重力场模型相比，谱组合模型精度明显提升。

地球重力场模型；谱组合法；卫星跟踪卫星；卫星重力梯度；GRACE；GOCE

1 引言

未来地球重力场模型化的挑战之一是如何将不同类型的重力测量数据进行联合处理，其解算结果广泛适用于大地水准面的确定和资源探测等方面。目前，重力测量手段主要包括卫星重力、卫星测高、航空重力、地面和船载重力测量等。不同的重力测量技术，由于其以不同的视角观测地球重力场，因此，包含了不同波段的重力场信息[1-5]。由CHAMP(Challenging Mini-Satellite Payload)和GRACE(Gravity Recovery and Climate Experiment)卫星测量任务提供的高低卫星跟踪卫星(SST-hl：High-low SST)和低低卫星跟踪卫星(SST-ll：Low-low SST)数据主要反映了地球重力场的中低频信息，这使目前已有的地球重力场低频信息更加可靠。但是这些数据有带宽限制，利用该类数据恢复地球重力场模型的有效阶次在120阶左右，如果需要恢复高阶(超过300阶)地球重力场模型，仅利用SST-hl/SST-ll数据显然是不合理的。而GOCE(Gravity Field and Steady-state Ocean Circulation Explorer)卫星测量任务提供的卫星重力梯度数据以及卫星测高、航空、地面和船测等重力测量任务提供的重力异常等数据，则主要反映了地球重力场的中高频信息[6,7]。因此，要构建超高阶的地球重力场模型、实现恢复厘米级精度大地水准面的宏伟目标，就必须将所有可用的不同类型重力测量数据进行融合处理。

目前，利用不同类型重力测量数据恢复地球重力场模型的融合处理方法主要有联合平差法[3，8，9]、谱组合法[4，9～17]、最小二乘配置法(LSC：Least squares collocation)、多输入/单输出法(MI/SO：Multiple-input/Single-output)、局部剪裁法[18]、迭代法[5]和大地测量超定边值问题法[9]等。

在不同类型重力测量数据融合处理研究方面，Schrama基于频域时域法对ARISTOTELES(Application and Research Involving Space Techniques Observing the Earth Field from Low-earth Orbit Satellite)计划中联合GPS(Global Positioning System)数据和SGG数据恢复重力场的精度与分辨率进行了误差模拟分析[19]，随后Visser对该问题做了进一步的研究和完善，指出联合GPS和SGG数据恢复重力场具有很好的频谱互补性[20]；Visser认为GRACE和GOCE任务是互补的，应该联合GRACE和GOCE卫星数据求解地球重力场模型[21]；Ditmar和Klees提出了基于时域法和空域快速解法联合SST和SGG观测数据求解GOCE重力场模型的方法，并通过数值试验分析了联合求解模型的精度以及该方法用于SST和SGG数据联合处理的适用性[22]；许厚泽等提出了用于重力场建模的超定边值问题局部剪裁解，在通用的单定边值问题局部剪裁法的基础上融进了大地水准面数据，使解算的模型较好地综合了重力异常和大地水准面的特性，能够较好地改善重力场模型中长波部分的精度[18]；Ditmar等讨论了单独使用SST观测量以及联合使用SST和SGG观测量求解重力场的精度，结果表明后者可以取得更好的结果[23]；Pail和Plank验证了半解析法用于联合SST和SGG数据恢复重力场的可行性，给出了利用GOCE数据恢复高精度高分辨率重力场的策略[24]；Zhu等将CHAMP(Challenging Mini-Satellite Payload)、GRACE和GPS卫星的观测数据进行联合平差处理，其与逐步平差或者单一观测数据的精度相比较，对高低卫星的星历、地心变化以及低阶位系数的精度有较大的改进[25]；徐新禹讨论了联合SGG和SST观测数据求解重力场的最优模型，给出了确定最优权的方差分量估计法和参数协方差法[3]；钟波推导出SST和SGG两类观测数据求解重力场的联合平差模型，并以地面重力异常为约束条件，导出以卫星轨道面和地面边界条件组成的二界面超定边值问题的随机边值解[9]；刘晓刚等以地面重力异常Δg为例，推导了利用迭代法联合不同类型重力测量数据反演地球重力场模型的基本原理公式并给出了其具体实现步骤，接着采用全球的重力异常Δg数据和扰动位T数据，基于迭代法对SGG数据解算的重力场模型进行进一步的精化[5]；钟波等论述了联合卫星轨道和重力梯度数据严密求解重力场的方法及数据处理方案，研究了GOCE重力场反演中有色噪声的AR去相关滤波、病态法方程的Kaula正则化和观测值最优加权的方差分量估计等关键问题[8]；Yi基于超过一年的GOCE测量数据获得了两个地球重力场模型，并对SGG数据进行带通滤波，对数据空白区进行约束，最后将GOCE的SGG数据模型与GRACE卫星数据模型组合起来，改进了GOCE模型在长波部分的精度[26]。

不同的融合处理方法存在其优缺点，本文仅研究谱组合法。国内外一些学者在谱组合法的研究上先期也做了大量工作，Wenzel和Sjöberg最早提出了利用谱组合对不同类型重力测量数据进行联合处理的想法[11，12]；Kern等在Wenzel和Sjöberg的研究基础上，对权函数的确定方法进行修改，将测量数据类型由两类扩展到多类，并采用多种数据类型和不同的组合方法对谱组合法的精度进行评估[13]；钟波等研究了联合高低卫-卫跟踪和卫星重力梯度数据恢复地球重力场的最小二乘谱组合法，基于球谐分析方法推导并建立卫星轨道面扰动位T和径向重力梯度Tzz以及扰动位Tzz和重力梯度分量组合Tzz-Txx-Tyy的谱组合计算模型与误差估计公式[9，14]；刘晓刚等给出了多种类型重力测量数据联合处理的谱权及谱组合的通用表达式，基于调和分析方法推导了由GOCE卫星SST和SGG数据构建地球重力场模型的谱组合公式及对应谱权的具体形式[4，15，16]；陆飚等针对GOCE和GRACE在地球重力场反演中的频谱互补性，研究联合GOCE和GRACE重力场模型位系数的谱组合法，给出了基于位系数误差阶方差定权、误差方差定权和块对角误差协方差定权的谱组合计算公式[17]。

在现有的文献中，除文献[17]外，其它文献基于调和分析方法，利用数据格网化误差确定各种观测数据的谱权，导致谱组合模型的计算精度不高。目前，国际上发布了很多由GRACE和GOCE数据构建的地球重力场模型，例如tongji-grace01和go-cons-gcf-2-tim-r5等。本文根据GRACE和GOCE数据恢复的重力场模型位系数的误差阶方差确定各模型对应的谱权，进而计算得到谱组合模型，并对其精度进行评估。

2 不同类型重力测量数据谱组合的基本原理

将不同重力测量技术得到的重力场参量ui分别作谱分解，以球谐函数的级数展开形式表示，有:

(1)

其中，n为位系数阶数；M为数据类型的个数；ui的方差和协方差分别为:

(2)

地球重力场参量u的最优估值可以根据下面的无偏估计模型来确定

(3)

(4)

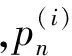
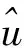
(5)

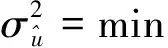
(6)

根据式(4)，并假设估计的谱分量之间相互独立，即当l≠n时，有σn,l(i,j)=0；进一步假设不同的重力测量技术得到的数据之间不相关，即当i≠j时，有σn,l(i,j)=0，则式(3)中各种重力数据对应的谱权为[9]:

(7)

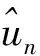
(8)

3 GRACE和GOCE的谱组合模型

解算的模型系数阶误差RMS为[27～29]:

(9)

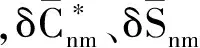
根据谱组合法的基本原理，谱组合公式实际上等价于位系数的谱组合，即：

(10)

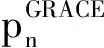
根据误差传播定律，得到谱组合模型位系数误差阶方差的计算公式为：

(13)

(14)

其中，R表示地球平均半径；N表示解算模型的阶数；γ表示地球正常重力，采用fM/R2近似计算。

因此，阶误差可以得到谱组合模型对应的大地水准面和重力异常误差阶方差：

(15)

(16)

进而可以得到谱组合模型对应的大地水准面和重力异常累计误差阶方差：

(17)

(18)

4 GRACE和GOCE数据模型介绍

tongji-grace01是同济大学采用JPL(Jet Propulsion laboratory)发布的实测GRACE RL02 Level-1B数据(星间K波段距离变率，约化动力学轨道以及加速度计和卫星姿态数据)，基于改进的短弧长积分法获得的纯GRACE数据静态地球重力场模型，数据时间跨度为2003～2007年共49个月。模型阶数达到160，不包含时变部分，没有采用正则化技术[30]。

go-cons-gcf-2-tim-r5是一个纯GOCE数据重力场模型，并未采用外部重力场信息作为参考模型或控制。该模型由其轨道和梯度数据联合解算，采用短弧长积分法处理运动学轨道数据，得到150阶的模型；梯度观测数据为梯度仪参考框架下(GRF：Gradiometer Reference Frame)的Vxx、Vyy、Vzz和Vxz，采用层叠滤波器对观测方程进行滤波，并利用调谐滤波器对87个独立的数据段进行滤波处理，得到280阶的模型。将Kaula正则化技术应用于带谐系数以提高信噪比，最优权比根据方差分量法来估计[31,32]。

为了对本文得到的谱组合模型精度进行评估，这里采用go-cons-gcf-2-dir-r5模型作为对比。该模型由GRACE、GOCE和LAGEOS数据构造而成，其中GOCE数据的时间跨度为2009年11月1日至2013年10月20日。为了处理GOCE卫星重力梯度数据，引入了260阶的先验模型go-cons-gcf-2-dir-r4。GOCE卫星重力梯度数据的处理并未采用外部校准，观测方程采用8.3～125.0mHz的带通滤波器进行滤波处理，随后对300阶的SGG法方程分别进行计算，共包括42个连续的时间段，总计1259天。梯度数据采用Vxx、Vyy、Vzz和Vxz分量，各分量的法方程相对权比为1，但是在SGG各分量的内部，所有观测方程的权比是根据其相对于先验模型的标准差来各自计算。为了克服由于极区空白引起的SGG法方程的不稳定性以及为了补偿GOCE测量数据对模型低阶系数的不敏感性，采用如下措施：(1)SGG法方程与一个GRACE法方程进行组合；(2)低于130阶时采用GRACE/LAGEOS数据，并利用球冠正则化技术进行迭代计算；(3)对超过180阶的部分应用Kaula正则化技术。通过对法方程组进行Cholesky分解，从而得到最终解。采用2003～2012共10年的GRACE数据计算了175阶的模型，在与GOCE数据融合时，GRACE的贡献为130阶。由于低阶部分，特别是2和3阶，并不能由GRACE和GOCE数据准确估算，因此，采用1985～2010年的LAGEOS数据来改进模型解。go-cons-gcf-2-dir-r5是由GOCE卫星重力梯度数据、GRACE和LAGEOS数据联合解算的纯卫星数据模型，因此与GPS/水准一样可以获得很好的轨道拟合[33～36]。

5 数值实验与结果分析

利用公式(10)对tongji-grace01和go-cons-gcf-2-tim-r5进行组合，得到谱组合模型，这里用grace+goce表示。图1表示不同重力场模型阶误差RMS、累计大地水准面误差和累计重力异常误差，不同重力场模型的精度统计结果见表1。

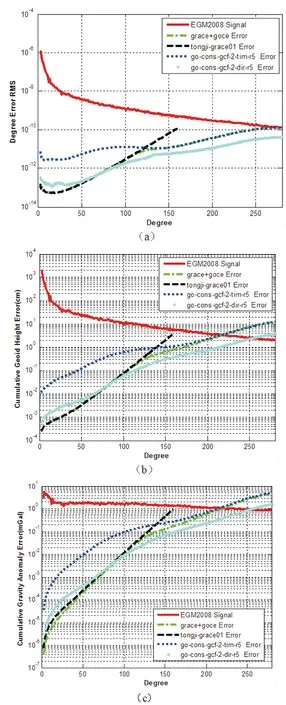
图1 不同重力场模型阶误差RMS、累计大地水准面和累计重力异常误差(a)重力场模型阶误差RMS；(b)累计大地水准面误差；(c)累计重力异常误差

表1 不同重力场模型的精度统计结果

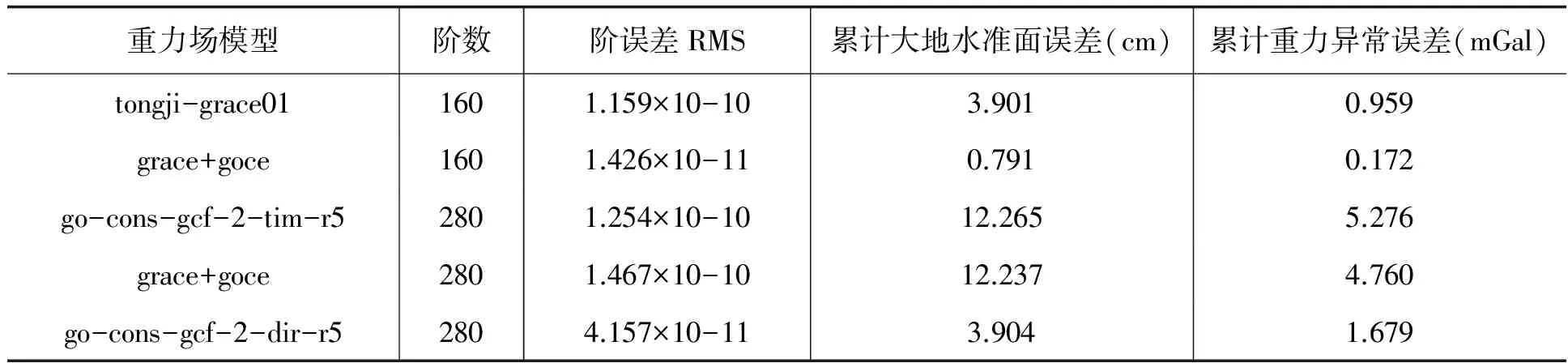
重力场模型阶数阶误差RMS累计大地水准面误差(cm)累计重力异常误差(mGal)tongji-grace011601．159×10-103．9010．959grace+goce1601．426×10-110．7910．172go-cons-gcf-2-tim-r52801．254×10-1012．2655．276grace+goce2801．467×10-1012．2374．760go-cons-gcf-2-dir-r52804．157×10-113．9041．679

根据图1和表1，可以看出：

tongji-grace01模型的精度在140阶之前要优于go-cons-gcf-2-tim-r5模型，并且该模型的有效阶次是160。GRACE卫星是第一个将低低卫星跟踪卫星和高低卫星跟踪卫星技术相结合的卫星任务，利用它的测量数据恢复的地球重力场模型，将使中长波长的球谐系数精度提高约2个量级。

go-cons-gcf-2-tim-r5模型的精度在140阶之后优于tongji-grace01模型，并且该模型的有效阶次为220。GOCE卫星是第一个将卫星重力梯度和高低卫星跟踪卫星技术相结合的卫星任务，其主要用于测定高阶静态地球重力场，相比CHAMP和GRACE卫星任务而言，利用它的测量数据恢复的地球重力场模型，使重力场中短波尺度的球谐系数精度有了较大程度的提高，又因为go-cons-gcf-2-tim-r5是采用轨道数据和重力梯度数据联合解算的模型，因此它在中长波尺度的球谐系数精度优于tongji-grace01。

低于160阶时，grace+goce模型的精度优于tongji-grace01；高于160阶时，grace+goce模型的精度优于go-cons-gcf-2-tim-r5模型，并且该模型的有效阶次为220。grace+goce模型在低于120阶时接近于tongji-grace01模型，而在220～280阶时接近于go-cons-gcf-2-tim-r5，因此得到了兼顾tongji-grace01和go-cons-gcf-2-tim-r5模型的最优联合解。grace+goce模型的累计大地水准面精度优于go-cons-gcf-2-tim-r5模型约0.03cm，累计重力异常精度优于约0.5mGal。

总体来看，由GRACE、GOCE和LAGEOS数据解算的go-cons-gcf-2-dir-r5精度优于谱组合模型grace+goce，并且该模型的有效阶次为250。但从具体细节来看，grace+goce模型在80阶之前优于go-cons-gcf-2-dir-r5模型，这是因为在构建grace+goce模型时采用的tongji-grace01模型精度非常高，优于同类的其它模型；而且grace+goce模型在构建时使用了GOCE卫星的轨道数据，因而改进了grace+goce模型在中长波部分的精度。相比较而言，go-cons-gcf-2-dir-r5模型仅使用了GOCE卫星的SGG数据。go-cons-gcf-2-dir-r5模型的累计大地水准面精度优于grace+goce模型约7.3cm，累计重力异常精度优于约3.1mGal。

6 结论

综合上述分析可以得出以下结论：

1)GRACE数据可以改善GOCE数据模型在中长波部分的精度，从而提高谱组合模型的整体精度。

2)与单一卫星数据解算的重力场模型相比，谱组合模型精度有了一定程度的提高，说明了谱组合法的有效性。

3)谱组合法原理简单，对计算机的存储和计算能力要求很低，因此，在计算时速度很快，在算法上也比较容易实现，可以对不同类型的重力场模型进行联合处理；其缺点是重力场模型的位系数必须已知，并且需要位系数的精度估计信息。

4)地面和航空重力测量数据可以进一步提高谱组合模型在中短波部分的精度，这将是本文下一步的研究工作。

[1]罗志才. 利用卫星重力梯度数据确定地球重力场的理论与方法[D]. 武汉: 武汉测绘科技大学, 1996.

[2]张传定. 卫星重力测量——基础、模型化方法与数据处理算法[D]. 郑州: 信息工程大学, 2000.

[3]徐新禹. 利用卫星重力梯度及卫星跟踪卫星数据确定地球重力场的研究[D]. 武汉: 武汉大学, 2008.

[4]刘晓刚. GOCE卫星测量恢复地球重力场模型的理论与方法[D]. 郑州: 信息工程大学, 2011.

[5]刘晓刚, 庞振兴, 吴娟. 联合不同类型重力测量数据确定地球重力场模型的迭代法[J]. 地球物理学进展, 2012, 27(6): 2342-2347.

[6]于锦海, 万晓云. 利用引力梯度不变量解算的GOCE引力场模型[J]. 中国科学D辑: 地球科学, 2012, 42(9): 1450-1458.

[7]万晓云. 基于GOCE梯度数据的引力场反演及应用[D]．北京：中国科学院大学，2013.

[8]钟波，宁津生，罗志才等．联合GOCE卫星轨道和重力梯度数据严密求解重力场的模拟研究[J]. 武汉大学学报(信息科学版)，2012, 37(10): 1215-1220.

[9]钟波. 基于GOCE卫星重力测量技术确定地球重力场的研究[D]. 武汉: 武汉大学, 2010.

[10]Wenzel H G. Zur geoidbestimmung durch kombination von schweranomalien und einem kugelfunktionsmodell mit hilfe von integralformeln[J]. Z Vermess, 1981(3): 102-111.

[11]Wenzel H G.Geoid computation by least squares spectral combination using integral kernels[C]. Proceedings of Symposium No.46 “Geoid Definition and Determination”, General Meeting of IAG, Tokyo, 1982.

[12]Sjöberg L E. Least squares combination of satellite and terrestrial data in physical geodesy[J]. Ann. Geophys., 1981(37): 25-30.

[13]Kern M, Schwarz K P, Sneeuw N. A study on the combination of satellite, airborne and terrestrial gravity data[J]. Journal of Geodesy, 2003(77): 217-225.

[14]钟波，罗志才，李建成等．联合高低卫-卫跟踪和卫星重力梯度数据恢复地球重力场的谱组合法[J]. 测绘学报，2012, 41(5): 735-742.

[15]刘晓刚, 孙中苗, 肖云等. 利用GOCE卫星的SST和SGG数据构建地球重力场模型[C]:大连：中国测绘学会大地测量专业委员会2013学术年会论文集, 2013.

[16]刘晓刚, 孙中苗, 肖云等. 利用多种类型重力测量数据确定地球重力场模型的谱组合法[C].北京：中国测绘学会第十次全国会员代表大会暨2013年学术年会论文集, 2013.

[17]陆飚, 钟波, 倪苇. 联合GOCE和GRACE重力场模型位系数的谱组合法[J]. 大地测量与地球动力学, 2014, 34(2): 155-160.

[18]许厚泽, 陆洋, 张克非. 测高-重力边值问题的局部剪裁解[J]. 测绘学报, 2002, 31(Sup.): 12-15.

[19]Schrama E J O. Gravity field error analysis: applications of global positioning system receivers and gradiometers on low orbiting platforms[J]. Journal of Geophysical Research, 1991, 96(B12): 20041-20051.

[20]Visser P N A M, Wakker K F, Ambrosius B A C. Global gravity field recovery from the ARISTOTELES satellite mission[J]. Journal of Geophysical Research, 1994, 99(B2): 2841-2851.

[21]Visser P N A M. Gravity field determination with GOCE and GRACE[J]. Adv. Space Res., 1999, 23(4): 771-776.

[22]Ditmar P, Klees R. A method to compute the Earth's gravity field from SGG/SST data to be acquired by the GOCE satellite[M]. Delft: Delft University Press, 2002.

[23]Ditmar P, Visser P, Klees R. On the joint inversion of SGG and SST data from the GOCE mission[J]. Advances in Geosciences, 2003(1): 87-94.

[24]Pail R, Plank G. GOCE gravity field processing strategy[J]. Stud. Geophys. Geod., 2004(48): 289-309.

[25]Zhu S, Reigber C, König R. Integrated adjustment of CHAMP, GRACE and GPS data[J]. Journal of Geodesy, 2004(78): 103-108.

[26]Yi W Y. An alternative computation of a gravity field model from GOCE[J]. Advances in Space Research, 2012(59): 371-384.

[27]李迎春．利用卫星重力梯度测量数据恢复地球重力场的理论与方法[D]．郑州：信息工程大学，2004．

[28]吴星. 卫星重力梯度数据处理理论与方法[D]. 郑州: 信息工程大学, 2009.

[29]刘晓刚, 张莹, 李靖等. 三种由卫星重力测量数据构建的地球重力场模型的精度评析[J]. 测绘科学与工程, 2013, 33(2): 19-24, 28.

[30]Shen Y, Chen Q, Hsu H, Zhang X, Lou L. A modified short arc approach for recovering gravity field model[C]. Oral presentation at the GRACE Science Meeting, University of Texas,2013.

[31]Pail R, Goiginger H, Mayrhofer R, et al. Global gravity field model derived from orbit and gradiometry data applying the time-wise method[C]. Proceedings of ESA Living Planet Symposium, Bergen, Norway, 2010.

[32]Pail R, Bruinsma S, Migliaccio F, et al. First GOCE gravity field models derived by three different approaches[J]. Jounal of Geodesy, 2011,85(11):819-843.

[33]Bruinsma S L, Marty J C, Balmino G, et al. GOCE gravity field recovery by means of the direct numerical method[C]. Presented at the ESA Living Planet Symposium, Bergen, Norway,2010.

[34]Bruinsma S, Foerste C, Abrikosov O, et al. The new ESA satellite-only gravity field model via the direct approach[J]. Geophysical Research Letters, 2013, 40(14): 3607-3612.

[35]Dahle C, Flechtner F, Gruber C, et al. GFZ GRACE level-2 processing standards document for level-2 product release 0005[R]. Scientific Technical Report,2012.

[36]Metzler B, Pail R. GOCE data processing: the sperical cap regularization approach[J]. Stud. Geophys. Geod. 2005(49): 441-462.

Fusion Processing of GRACE and GOCE EGMs Based on Spectral Combination

Liu Xiaogang1,2，Xiao Yun1,2，Ouyang Mingda3,4，Li Yingchun1,2

1. Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China 2. State Key Laboratory of Geo-information Engineering, Xi’an 710054, China 3. Institute of Geospatial Information，Information Engineering University，Zhengzhou 450001，China 4. Technical Division of Surveying and Mapping，Xi’an 710054，China

The paper discusses the basic principle of spectral combination and presents the general expressions of the spectral weight and spectral combination of various types of gravimetric data in fusion processing. Based on the degree variance of potential coefficients, the paper derives the detailed expressions of spectral combination formulae and the corresponding spectral weights in the EGM according to GRACE and GOCE data. Besides the paper constructs a spectral combination model according to the tongji-grace01 and go-cons-gcf-2-tim-r5 model using spectral combination method, and compares the accuracy of the results obtained with that of go-cons-gcf-2-dir-r5 model. The experiment results show that the GRACE data model can improve the accuracy of GOCE data model in medium-long wavelength, thus, it improves the overall accuracy of fusion model. Moreover, the accuracy of spectral combination model is better than that of the single-satellite model recovered by GRACE and GOCE data.

earth gravitational field model(EGM)；spectral combination method； satellite-to-satellite tracking (SST)；satellite gravity gradient (SGG)；GRACE；GOCE

2015-04-16。

国家自然科学基金资助项目(41304022)，国家973计划资助项目(61322201，2013CB733303)，高分专项青年创新基金资助项目(GFZX04060103-5-12)。

刘晓刚(1983—)，男，助理研究员，主要从事卫星重力、磁力测量方面的研究。

P228