基于夏氏法的螺栓连接结构传递函数辨识
2015-04-19王银惠赵俊生焦欢庆丁爱国
□ 王银惠 □ 赵俊生 □ 焦欢庆 □ 丁爱国
中北大学机械与动力工程学院 太原 030051
1 螺栓连接结构系统的设计
螺栓连接结构是一种常用构件的连接方式,其在机械结构中应用广泛。随着有限元分析技术的发展,应用CAE软件优化分析机械结构已逐步成熟,但其中有关接触问题的简化程度是影响分析精度的主要因素,而工程机械中诸多零部件间均采用螺栓连接[1]。为具体分析螺栓连接结构在复杂弹性体中的传递特性[2],笔者设计一个螺栓连接系统,利用Pro/E建立三维模型(如图1所示),两个实心的T型圆柱杆由3个M14的六角头螺栓连接。
2 有限元模型中螺栓连接的简化方式
2.1 第一种简化方式
如图2所示,该简化方式是将螺栓杆结构简化成一根圆柱形的梁单元,其半径与螺栓的实际半径相等,梁单元的端部采用刚性单元与被连接件相连接,刚性单元的连接点一般取在以螺栓杆中心线为中心的圆上,用于模拟螺栓与被连接件之间的相对位置关系。
2.2 第二种简化方式
如图3所示,通过对螺栓结构分析,将螺栓和螺母结构简化成哑铃结构的刚性体。通过建立面与面之间对应网格节点的耦合关系,来控制相接触的被连接件之间的侵入和模拟它们之间的摩擦锁紧;同时配合螺栓预紧力的施加,来准确模拟螺栓连接区域的力学性能,以便较准确模拟构件的真实情况。在螺栓连接结构中间截面处添加大小为100 N的预紧力,分别定义螺栓与杆件的接触面,并设定为小滑移,设置接触控制为自动容差控制。
2.3 模态分析及连接试验
导入Pro/E建立的试验模型,利用Hyper Mesh 软件[10]进行前处理[3],材料属性定义弹性模量为 212 GPa,泊松比为 0.288,密度为7.83 g/cm3,所划分的有限元模型节点数为1 296,单元数为4 170。定义接触分析,约束位置为变截面处,即模态试验构件悬吊位置,通过模态分析得到该连接构件的各阶振型及固有频率,振型如图4所示。在第一种简化情况下,连接构件在低阶频率下连接正常,但在高阶频率下构件已经出现错位现象。
为进一步分析有限元模型与真实构件的误差程度,采用Q235-A钢试制模型,螺栓等级为8级的全螺纹六角头螺栓,连接后加载相应预紧力,进行模态试验,结果见表1。

▲图1 螺栓连接系统模型

▲图2 第一种简化方式

▲图3 第二种简化方式
对比发现,一~六阶对应模态频率,两种简化方式对应模态频率与试验频率存在很大偏差,这是因为试验模态中传感器等部件的安装给试验带来一定误差,但由于自由模态都接近于0,可以认为简化有效;而七~十阶对应模态频率,第一种简化方式相对第二种简化方式,有限元模态频率与试验模态频率存在误差较大,因此,选择第二种简化方式进行螺栓连接[8]结构传递函数的辨识。
3 夏氏偏差修正辨识
夏氏法[4]即一种交替的广义最小二乘法,不仅消去最小二乘法估计中的偏差,又避免了广义最小二乘法中数据反复过滤,具有较高精度和较高计算效率。方法如下,式(1)为最小二乘法辨识表达式,式(2)为广义最小二乘法辨识表达式。

式中:y为 N维输出向量;ξ为N维输入向量;θ为(2n+1)维参数向量;Φ 为 N(2n+1)测量矩阵。ε为系统输入的白噪声;ξ2为系统的输出白噪声;Ω为残差构造;f为辨识参数向量。

▲图4 第一种简化方式各阶振型图

表1 螺栓连接结构试验模态和有限元模态频率
应用最小二乘法可得到参数估值:
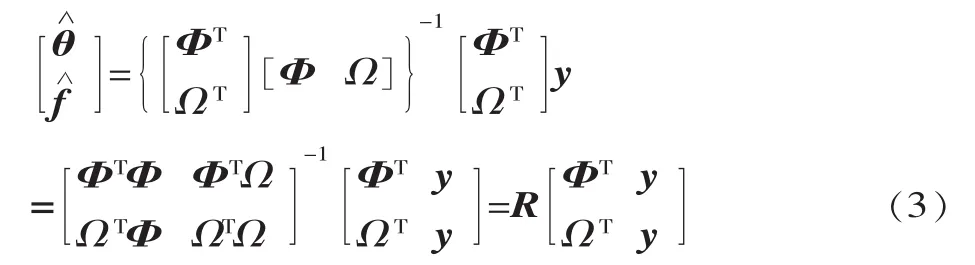
令:
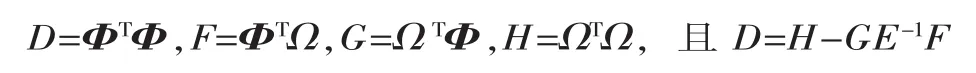

则有:D=ΩTMΩ,其中:M=I-Φ(ΦTΦ)-1ΦT,因此得:

化简得到:
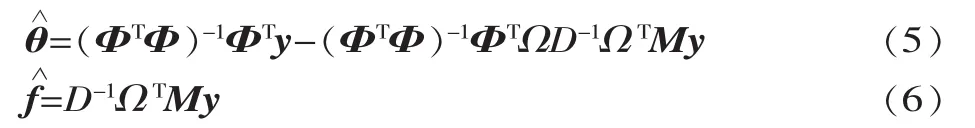
将式(6)代入式(5)式得:

(4)返回到第二步,重复上述计算过程,一直到θB保持不变为止。
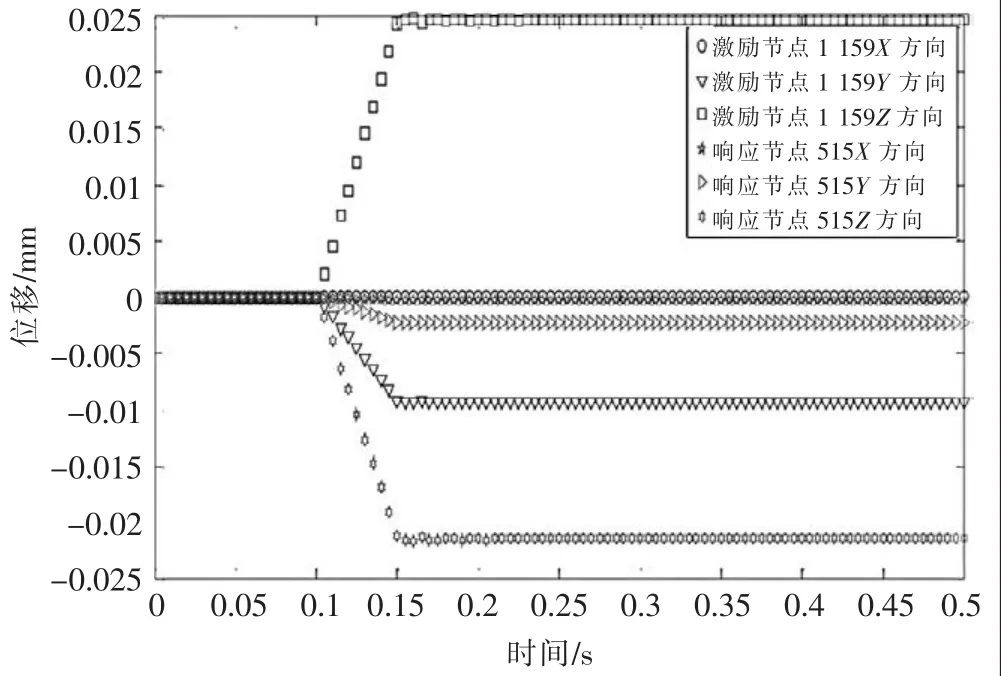
▲图5 激励点、响应点位移
4 螺栓连接结构传递函数辨识
在螺栓连接结构有限元模型1 159节点上添加瞬态载荷,通过Opti Struct求 解 器[7]分析计算,得到响应点515节点的位移数据,得到激励点和响应点的位移图像,如图5所示。通过比较,发现激励通过系统后,Y向振动幅值变大,Z向相对减小且方向相反。
将1 159与515节点之间看成一个黑箱系统[9],采用夏氏偏差修正法对结构传递特性进行辨识,利用MATLAB软件编程实现。辨识流程如图6所示。
通过辨识,求得激励点1 159与响应点515之间的传递函数为:

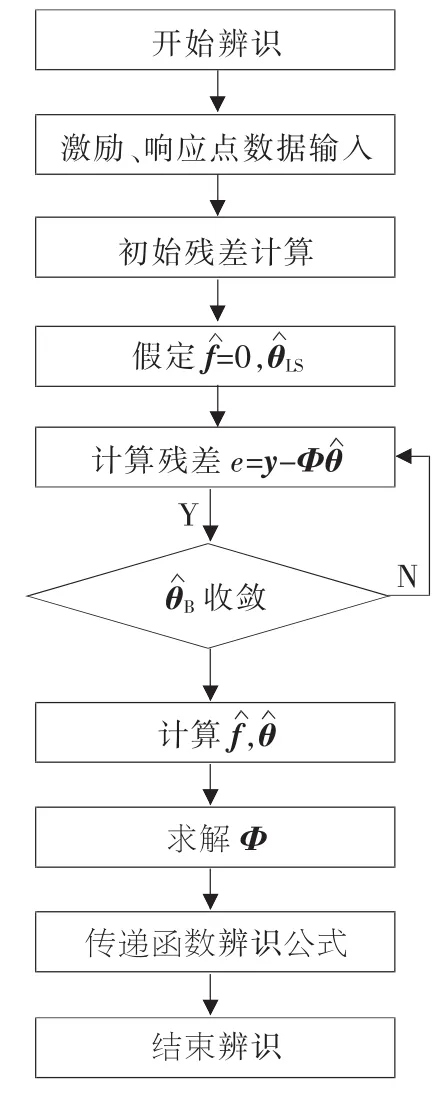
▲图6 夏氏法传递函数辨识流程图
式中:s为通过数学表达式所描述系统的常微分方程经过拉氏变换后的变量。
5 结论
对于螺栓连接结构的有限元模型,在确定的预紧力及接触表面情况下,将螺栓简化成哑铃型结构,在定义好接触单元的情况下,该模型仿真效果较好。采用夏氏法可以对含有螺栓连接的组合弹性体传递函数进行辨识,其不仅有较高精度和较高的计算效率,而且具有较广范围的拓展性。
[1]陈学前,杜强,冯加权,等.螺栓连接非线性振动特性研究[J].振动与冲击,2009,28(7):196-198.
[2]武新峰,雷勇军,李家文,等.基于有限元分析的复杂结构弹性振动传递函数建模[J].振动与冲击,2012(11):57-61.
[3]杨毅春,李东波,史翔,等.基于HyperMesh的三维螺旋体网格划分与建模研究[J].煤矿机械,2013,34(3):79-81.
[5]倪振华.振动力学[M].西安:西安交通大学出版社,1994.
[6]李言俊,张科.系统辨识理论及应用[M].北京:国防工业出版社,2009.
[7]王钰栋,金磊,洪清泉,等.Opti Struct&Hyper Study理论基础与应用[M].北京:机械工业出版社,2012.
[8]马志豪,徐斌,王子延,等.柴油机连杆螺栓松动故障的诊断[J].河南科技大学学报(自然科学版),2003,24(3):47-50.
[9]陈濬华,王彬,黎苏.内燃机结构传递函数的有限元计算[J].内燃机学报,1989,7(4):313-318.
[10]洪清泉.Hyper Mesh&Hyper View应用技巧与高级实例[M].北京:机械工业出版社,2012.
