水平轴风力机塔架在不同工况下的模态分析
2015-04-19胡世军李小强张恒磊刘守庆
□ 胡世军 □ 李 乐 □ 李小强 □ 张恒磊 □ 刘守庆
1.数字制造技术与应用省部共建教育部重点实验室 兰州 730050 2.兰州理工大学机电工程学院 兰州 730050
塔架是风力发电机的主要支撑装置,目前,该结构的设计一直以引进国外的设计为主,随着国内风力发电机塔架的大型化,有必要对风电塔架结构进行详尽的分析[1-2]。水平轴风力机塔架的顶端安装有较大质量的机舱和旋转的风轮,在风力发电机工作时,塔架所受的动力作用主要有2种,即风轮转动的激励作用和风载荷作用[3]。无论是风轮激励还是风载荷作用而造成的塔架动态响应,除了和作用载荷本身的大小以及随时间的变化规律有关外,还取决于结构本身的自振频率特性[4]。笔者以某1.5 MW风力机塔架为研究对象,探讨了塔架在有无基础、有无门洞4种工况条件下的动态特性,对今后塔架的设计具有一定的参考意义。
1 塔架的简化模型
该塔架是圆筒式的钢材结构,高度72 m,底部直径4.2 m,顶部直径3.0 m,最大壁厚26 mm,最小壁厚12 mm,由3段圆筒用法兰盘连接而成,结构为壁厚渐变空心圆柱状。塔架质量145.1 t,机舱质量60 t,风轮质量30 t,偏心距0.2 m。塔架材料为Q345-C钢,屈服强度σs=325~345 MPa。建立模型时以新疆达坂城风力发电厂某定型风力发电机组塔架为例,作如下简化。
(1)由于爬梯、休息平台主要承受竖向载荷,并且与塔架之间为软连接,故可将其质量附加到塔筒上。
(2)在塔架顶端机头质心位置创建一个质量单元节点,将其设置为机舱和叶片的总质量,然后用载荷伞将其与塔顶单元节点相连接。
2 塔架的模态分析
2.1 塔架振动微分方程的建立
塔架系统模态计算就是将塔架模型离散成为具有有限个自由度的多自由度系统,分别计算多自由度系统中每个自由度的模态参数并将其线性叠加。对于具有n个自由度的物理模型,则需要n个独立的坐标系对其进行求解。n个主振动的叠加构成了系统的自由振动响应,即可得到系统各阶的固有频率与振型。
对于n个自由度系统,以广义坐标q(t)表示的运动微分方程为:

式中:[m]、[c]、[k]分别为塔架整体的质量矩阵、阻尼矩阵以及刚度矩阵;分别为节点的位移、速度和加速度列阵;{F(t)}为外部载荷激励列 阵[5]。
若式(1)右端项F=0,在非零的初始条件下,方程有非零解,这时塔架处于自由振动状态。由于没有外载荷作用,方程的解反映了结构本身固有的特性,即频率与振型。
2.2 塔架有限元模型的建立
笔者选用8节点Shell281单元类型,定义材料弹性模量 E=206 GPa、泊松比 μ=0.3、密度 ρ=7 850 kg/m3。在ANSYS中直接建立几何模型,选取单元资料,然后定义塔架单元,网格划分时单元边长为0.5 m,经网格划分器MeshTool处理,利用映射网格划分和自由网格划分相结合的方式,将塔架模型离散为12 799个节点,得到如图1和图2所示的塔架有限元模型。选用8节点Solid185单元,利用自由网格划分方式,将有基础模型离散为2 433个节点,得到如图3和图4所示的塔架有限元模型。
2.3 塔架模态分析方案
(1)无基础有、无门洞情况下塔架的模态分析。塔架底部所有节点的滑移自由度和旋转自由度均为零,风力机塔架所承受的静载荷除自重外,还有来自顶部的风力机和叶轮的重力偏心载荷,采用Block Lanczos法提取前五阶模态。同理,对塔架底端开有1.8 m×0.6 m的门洞,提取前五阶模态。

▲图1 无基础塔架的有限元模型

▲图2 舱门局部放大图

▲图3 有基础塔架的有限元模型

▲图4 舱门基础放大图
(2)有基础有、无门洞情况下塔架的模态分析。将塔架固定在长9 m、高3 m的八棱台上,材料密度为4 600 kg/m3,弹性模量为 28 GPa,泊松比为 0.25,且塔架模型与基础模型用MPC多点约束,风力机塔架所承受的静载荷除自重外,还有来自顶部的风力机和叶轮的重力偏心载荷,采用Block Lanczos法提取前五阶模态。同理,对塔架底端开有1.8 m×0.6 m的门洞,提取前五阶模态。
2.4 4种工况下的求解
在加载和求解过程中,选用模态分析类型,定义扩展模态数为5,在风力机塔架的模态分析中,无论有无门洞还是是否考虑基础,低频振动都要比高频振动危险且低阶模态占主要状态,高阶模态对响应的贡献很小,阶数越高,其贡献就越小。而且,由于结构阻尼的作用,响应中的高阶部分衰减也很快,故对高阶模态可以忽略不计。根据上述特点,只计算了塔架的前五阶模态,见表 1~表 4。
3 结果分析
如图5和图6所示,对于无基础的塔架而言,无论有无门洞,第一、二阶频率分别为2个方向上的一阶弯曲振型,第三、四阶频率分别为2个方向上的一阶扭转振型,第五阶频率为二阶弯曲振型。
如图7和图8所示,对于有基础的塔架而言,无论有无门洞,第一、二阶频率分别为2个方向上的一阶弯曲振型,第三、四阶频率分别为2个方向上的二阶弯曲振型,第五阶频率为一阶扭转振型。
分析结果表明,低阶模态中,无基础无门洞塔架的固有频率最大,无基础有门洞塔架次之,有基础有门洞塔架固有频率最小。这说明门洞和基础都会降低塔架的固有频率,但是基础对塔架的影响要比门洞大得多,因此,门洞对塔架固有频率的影响可以忽略不计。
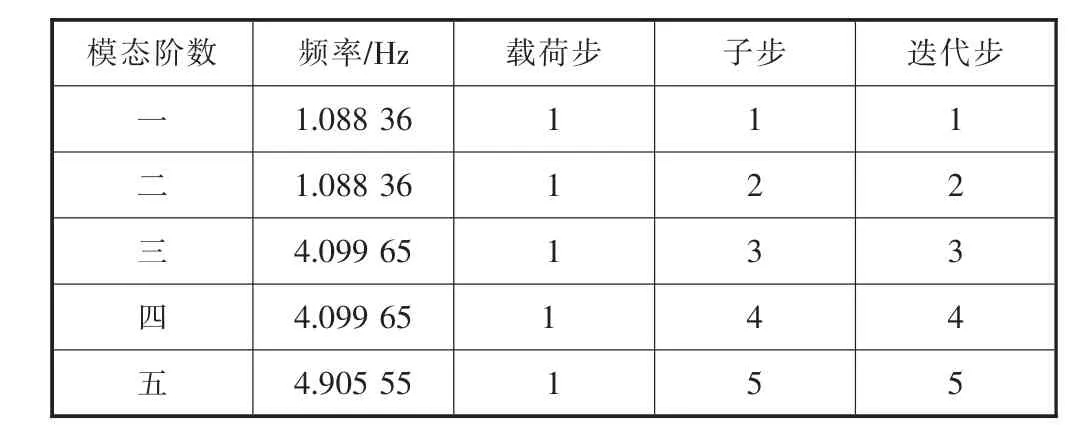
表1 无基础无门洞塔架前五阶频率
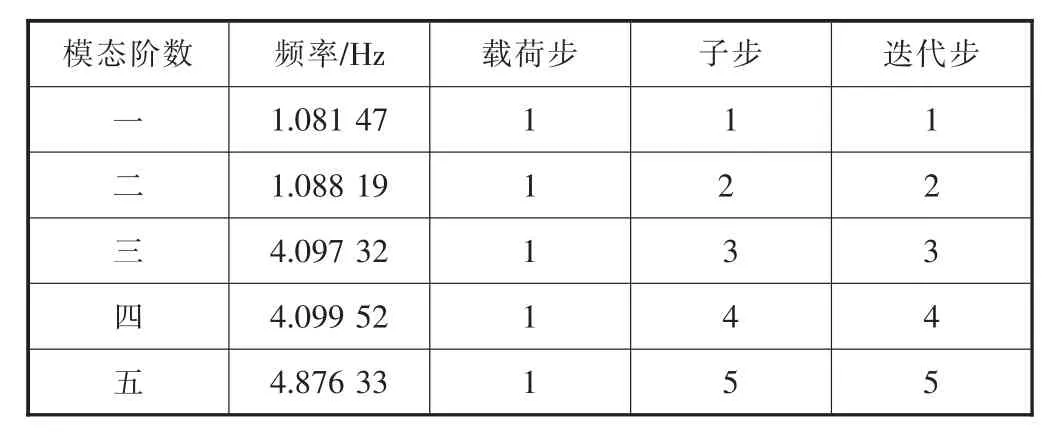
表2 无基础有门洞塔架前五阶频率
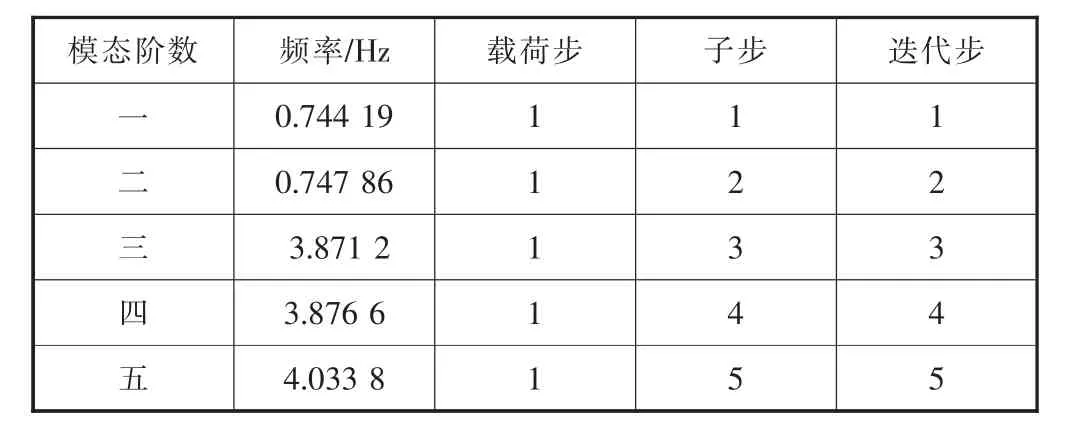
表3 有基础无门洞塔架前五阶频率
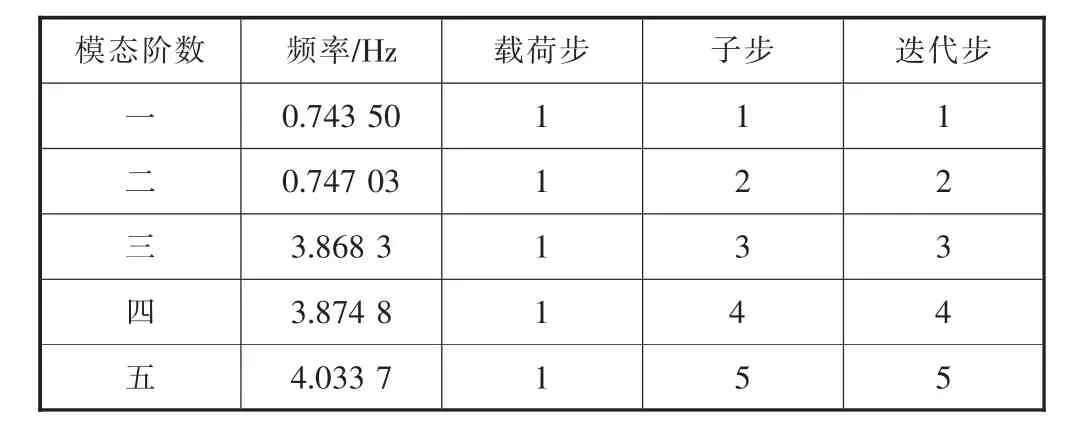
表4 有基础有门洞塔架前五阶频率
笔者所研究的塔架风轮转速为18.2 r/min,工作频率f=0.303 33 Hz,3f=0.91 Hz。塔架与风轮不发生共振的条件是,塔架的固有频率与风轮的工作频率或风轮3倍的工作频率之间相对差大于10%。因此本文所研究的塔架不会发生共振。

▲图5 无基础无门洞前五阶振型图

▲图6 无基础有门洞前五阶振型图

▲图7 有基础无门洞前五阶振型图
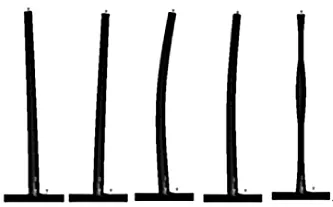
▲图8 有基础有门洞前五阶振型图
4 结论
通过模态分析,可以确定风力发电机塔架的固有频率和固有振型,依据求解出来的固有频率,可以判断塔架在外载荷激励下是否会发生共振。虽然考虑门洞的情况下,塔架的固有频率会有所降低,但是门洞对塔架固有频率的影响很小,其作用可以忽略不计,考虑基础的情况下,塔架的固有频率明显降低,基础对塔架固有频率的影响很大。
塔架的固有频率不仅与材料、几何尺寸有关,还与塔架基础以及有无门洞有关。因此,在风力机塔架的动态设计中,不仅要考虑塔架的选材、结构尺寸的设计,还要考虑塔架基础对固有频率的影响。
[1]刘勇.基于有限元法的风力发电机塔架模态分析[J].装备制造技术,2011(3):41-44.
[2]Tavner P.Wind Power as a Clean-energy Contributor[J].Energy Policy,2008,36(12):4397-4400.
[3]崔阳.大型风力机组塔架静动态有限元分析[D].沈阳:沈阳工业大学,2010.
[4]李斌,姜福杰.风力发电机锥筒型塔架的模态分析[J].内蒙古科技大学学报,2009,28(4):364-368.
[5]李有堂.机械振动理论与应用[M].北京:科学出版社,2012.
