一类动态车辆路径问题模型和两阶段算法

饶卫振，金 淳，刘 锋，杨 磊

(1.山东科技大学经济管理学院，山东青岛266590；2.大连理工大学系统工程研究所，辽宁，大连116024；3.东北财经大学管理科学与工学院，辽宁，大连116025)

一类动态车辆路径问题模型和两阶段算法

饶卫振*1，金 淳2，刘 锋3，杨 磊1

(1.山东科技大学经济管理学院，山东青岛266590；2.大连理工大学系统工程研究所，辽宁，大连116024；3.东北财经大学管理科学与工学院，辽宁，大连116025)

针对一类动态车辆路径问题，分析4种主要类型动态信息对传统车辆路径问题的本质影响，将动态车辆路径问题(Dynamic Vehicle Routing Problem,DVRP)转化为多个静态的多车型开放式车辆路径问题(The Fleet Size and Mixed Open Vehicle Routing Problem,FSMOVRP)，并进一步转化为多个带能力约束车辆路径问题(Capacitated Vehicle Routing Problem,CVRP)，基于CVRP模型建立了DVRP模型；然后，在分析DVRP问题特点基础上，提出两阶段算法，第一阶段基于利用K-d trees对配送区域进行分割的策略，提出了复杂度仅为O(nlogn)的快速构建型算法，第二阶段通过分析算法搜索解空间结构原理，设计混合局部搜索算法；最后，基于现有12个大规模CVRP标准算例，设计并求解36个DVRP算例.求解结果表明了模型和两阶段算法的有效性.

物流工程；两阶段算法；动态车辆路径问题；K-d树分割策略；算法搜索解空间

1 引 言

车辆路径问题(Vehicle Routing Problem,VRP)自1959年Dantzig等[1]提出以来一直受到人们的广泛关注，其研究意义毋庸置疑.随着移动通讯(Global System of Mobile communication,GSM)、电子商务(Electronic Commerce,EC)、全球定位系统(Global Positioning System,GPS)和智能交通系统(Intelligence Transport System,ITS)等技术的发展，物流配送企业能够方便地获取顾客状态、交通路况和任务车辆状态等实时信息.因此，基于传统VRP问题考虑配送中实时信息的动态车辆路径问题(Dynamic Vehicle Routing Problem,DVRP)成为热点研究问题.

由于DVRP问题的理论和实践意义，自Psaraftis[2,3]在1988年提出DVRP问题以来，很多学者在该领域做了广泛研究[4]，如Larsen研究了DVRP问题的动态程度特征指标的计算方法[5]；Brotcorne等研究了急救车的动态调度问题，其主要考虑新客户的在线出现[6]；随后研究考虑实时交通 信 息 的 DVRP学 者 还 有 Taniguchi[7]和Fleischmann[8].Melachrinoudis考虑了医疗服务的特殊环境对DVRP问题的影响，并构建了相应模型[9].在最近2年里，Khouadjia[10]和Ferrucci[11]分别研究了具有动态客户的DVRP问题，并提出了相应的求解策略；Albareda-Sambola通过研究验证了将DVRP按时段分割处理的可行性[12]；Ghannadpour研究了多目标DVRP问题[13].针对DVRP问题，部分国内学者也进行了较为广泛的研究，如郭耀煌等在综述当前DVRP研究现状的基础上[14]，分别研究了DVRP问题的求解策略[15]和模型[16]；刘霞[17]和Hong[18]研究了带时间窗的DVRP问题；陈久梅等研究了装卸一体化的DVRP问题，并提出了分区求解策略[19].葛显龙研究了联合配送的开放式DVRP问题[20].

综上所述，当前已有部分学者对DVRP研究做了较为深入的研究，但当前针对DVRP的研究鲜见分析与VRP的本质区别，并且现有求解算法设计强调求解质量，而对算法合并动态事件生成新方案的速度方面考虑较少[4].本文通过分析发现，DVRP问题能够转化为多车型开放式车辆路径问题(The Fleet Size and Mixed Open Vehicle Routing Problem,FSMOVRP)，并进一步转化为经典的能力约束VRP问题(Capacitated VRP,CVRP).首先，基于经典的CVRP模型，建立了DVRP模型.然后，基于模型提出一个有效的两阶段算法，并通过设计和求解标准DVRP算例验证了本文模型与算法的有效性.

2 问题建模

2.1 问题分析

DVRP与传统的静态CVRP问题的主要区别是，在配送过程中会出现新的信息，本文称为动态事件.动态事件主要存在4种类型，包括：

(1)新顾客出现；

(2)老顾客改变需求；

(3)交通堵塞或中断；

(4)配送车辆抛锚.

本文研究的DVRP问题除了经典CVRP中的假设外还包括：

(1)如果是执行配送任务，设配送的货物为同质物品，每辆车均满载后开始执行任务；如果是回收任务，每辆车均空车开始执行任务.

(2)仅考虑局部交通中断情况(即局部发生严重的交通堵塞或道路管制问题)，不考虑大面积的交通瘫痪导致无可行方案的情况.

(3)车辆在出现抛锚后，在配送周期内不能够完全修理好.

当任何动态事件发生后，基于原有信息所得到的方案在当前情况下可能质量非常低劣甚至不可行，所以需要结合当前信息，对方案重新优化以及时修正方案.求解该问题关键在于，此时已有部分车辆完成部分配送服务，所在位置已不在配送中心.对于这样的车辆重新优化配送路线，等价于起点(终点)不在配送中心的开放式VRP(Open VRP,OVRP)问题，并且由于这些车辆已完成部分配送服务，此时服务能力为车辆所剩货物量，因此等价于多车型OVRP问题(The Fleet Size and Mixed OVRP,FSMOVRP).FSMOVRP问题可以进一步转化为CVRP问题，将不在配送中心的车辆起点或终点虚拟为一个顾客，且需求量为当前最大车载量Q与当前车型载量之差，并将该虚拟顾客设定为必须第一个(最后一个)接受服务的顾客.如图1(a)、图1(b)所示为出现新顾客后的一个DVRP问题，转化为一个CVRP问题示意图.

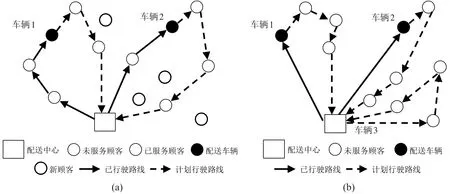
图1 DVRP转化为CVRP示意图Fig.1 A demonstration of transformation from DVRP to CVRP

同理，对于出现尚未服务的老顾客改变需求和车辆出现抛锚时，通过更新当前尚未服务的顾客可以做类似处理.而当出现交通中断时，相当于求解一个更新顾客间行驶成本后的CVRP问题，在此不再赘述.因此DVRP可以转化分解为多个CVRP问题.

2.2 数学模型

符号表示：

t0——配送开始时刻；

tend——配送结束时刻；

T——配送周期等于tend-t0；

s——整个配送周期T中动态事件(信息)出现的次数；

Eventi—— 第i次动态事件，1次动态事件指的是出现1次新信息，0≤i≤s；

EventTimei——第 i次动态事件发生的时刻，0≤i≤s，t0≤EventTimei＜tend，且 令EventTime0=t0；

n——所有出现的顾客数量；

ki——在时刻点EventTimei正要到达时在执行配送任务的车辆数量，ki≥0；

mi——在时刻点EventTimei正要到达时方案中车辆数量，显然mi≥ki；

Q——表示在配送中心车辆的最大服务能力；

L——表示单辆车的最大行程约束；

Qik——在时刻点EventTimei第k辆任务车辆已耗费的服务能力，0≤Qik≤Q，0≤i≤s，0≤k≤ki；

Lik——在时刻点EventTimei第k辆任务车辆已行驶的距离，0≤Lik≤L，0≤i≤s，0≤k≤ki；

v——所有车辆的行驶速度，为确保每辆车均能够在周期内完成任务设L/v≤0.5T；

Di——表示在时刻点EventTimei下的距离矩阵，其内部的元素为；

qi——顾客i的需求量，max(qi)≤Q,1≤i≤n.

δ——动态程度，等于在配送过程中出现新顾客的数量占总顾客数量的比率[5].

由以上分析得到，DVRP可以分解为(s+1)个CVRP问题，可得DVRP在时刻点EventTimei下的数学规划模型为

目标函数：

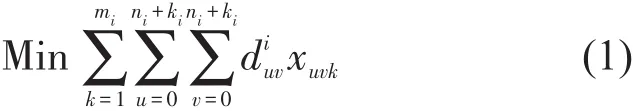
约束条件：

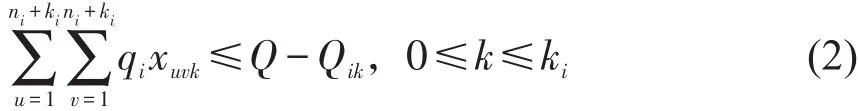
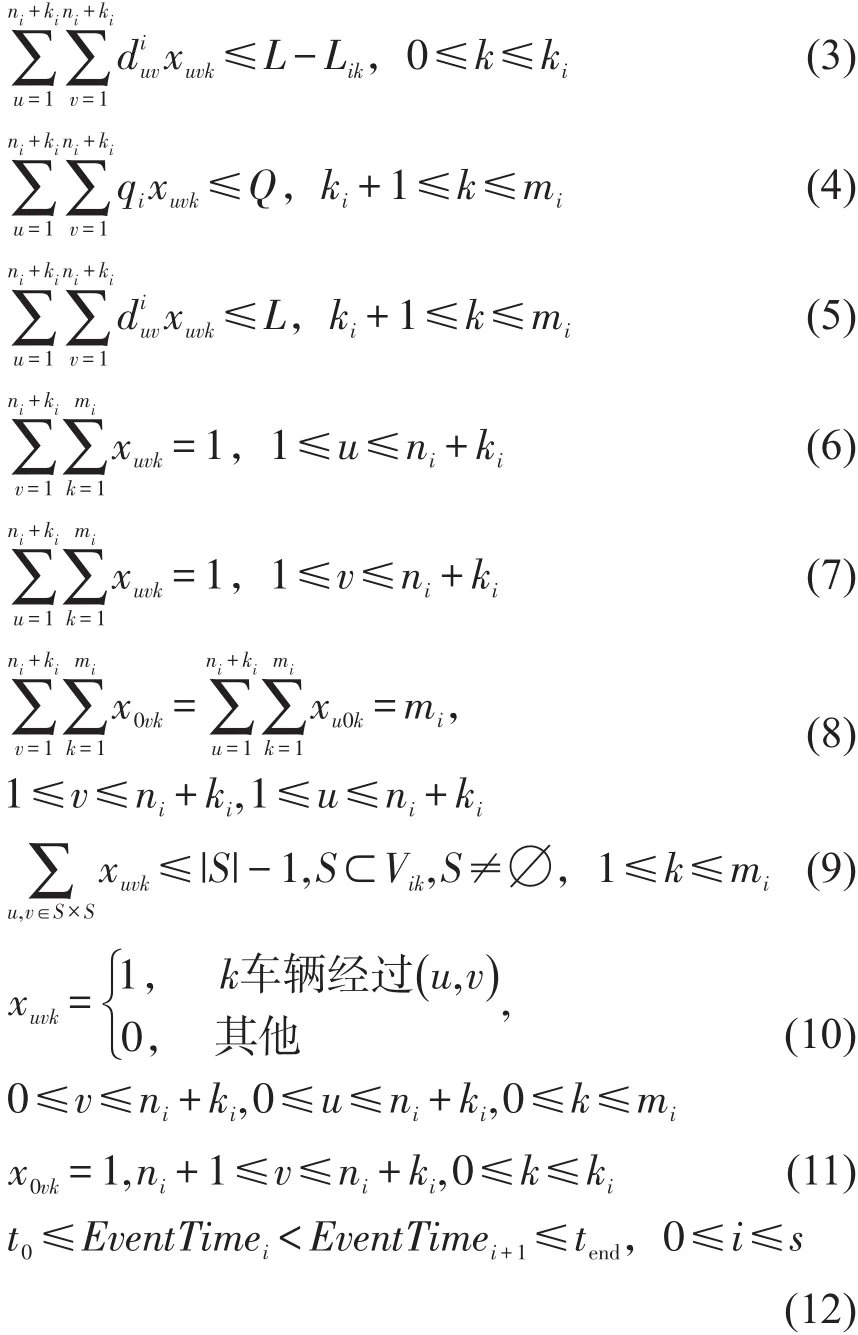
式(1)为总行程最小目标；式(2)和式(3)为车载量与行驶距离约束；式(4)和式(5)为计划从配送中心派送车辆的载量与行驶距离约束；式(6)和式(7)表示每个客户恰好仅被1辆车服务；式(8)约束了所有车辆的起终点都在配送中心；式(9)表示每辆车行驶的路径轨迹恰好为一个简单圈；式(10)为变量含义和取值；式(11)约束每辆正在执行任务的车辆必须首先服务当前所在位置对应的虚拟顾客，以使配送的路径为简单圈从而由FSMOVRP转化为CVRP问题.式(12)表示动态事件发生的时刻点在配送周期之内，且呈时间序列状态.

3 两阶段算法

根据上述建模思想，求解该模型的最大挑战在于对算法速度有非常高的要求.因为，当动态事件发生的比较频繁时，就要求算法能够在短时间内求解问题.本文设计了一个两阶段算法：改进贪婪算法和混合大邻域算法.采用该两阶段算法求解DVRP的流程图，如图2所示.

图2 两阶段算法求解DVRP流程图Fig.2 Flow chart of two-stage algorithms for solving dynamic vehicle routing problem

如图2所示，本文求解DVRP问题基于“先完成后完善”的思想.首先采用改进贪婪算法结合新的信息，快速生成一个质量满意的方案；然后充分利用下一个动态事件出现之前的这段时间，采用混合大邻域算法继续改进当前车辆的计划行驶路线；最后，当出现下一个动态事件后再重复这一过程，直到配送过程结束.

3.1 改进贪婪算法

经典贪婪算法(Greedy,GR)求解过程中初期效果非常好，但构造后期会导致质量迅速下降.另外，GR要求对任意2个顾客形成的距离从小到大排序，那么相当于对n(n-1)/2条边排序，根据排序算法GR算法的复杂度至少为O(n2logn)，该复杂度会随着n的增加而迅速增加.本文提出2个分别提高GR求解质量和求解速度的策略，得到改进GR(Improved GR,IMGR).

IMGR提高质量策略的思想是，让离配送中心较远的边更短，而离配送中心较近的边更长，从而GR将会优先连接离配送中心较远的点，使贪婪算法构造后期质量改进从而提高整体算法的质量；提高速度的策略是，据GR运算原理，其主要计算量为求最邻近点计算，并且实际物流配送中，两点间的路网距离和直线距离高度相关.在此，我们采用K-d trees(K-dimensional binary search trees)法近似求解区域中的最邻近点，本文将配送区域作为2维平面，因此K=2，其详细执行原理参照Bentley的文献[21].该算法的性能在求解大规模CVRP问题中已得到验证，结合K-d trees的IMGR的求解复杂度仅为O(nlogn)，并且求解世界上顾客数量达到20 000的规模最大标准算例的求解质量与理论最优解的偏差仅为5.18%[22].

3.2 混合大邻域算法

通过文献[23]研究旅行商问题(Traveling Salesman Problem,TSP)的求解算法发现，当算法搜索解空间结构(问题解空间中的可行解为节点，互为邻域的可行解之间存在边)类似于小世界网络时，其对应的算法求解质量更优，且只具有某一特定算法规则的算法，其解空间结构更类似于规则网络.

由于TSP是CVRP的子问题，因此其上述结论对CVRP具有一定借鉴意义.根据复杂网络理论可知，多个规则网络混合后得到的网络会更类似于小世界网络[24].因此，多个特定算法规则进行合理混合，就可能得到有效的算法.基于该思想，本文采用改进CVRP问题解的4种车辆路径间基本规则(Swap、Exchange、Cross-Exchange和Inter-relocate)和4种车辆路径中规则(2-opt、Lin-Kernighan、Intrarelocate和Or-opt)，设计了一个混合大邻域算法(Hybrid Large Neighborhood Algorithm,HLNA)，其求解规则伪代码如图3所示.

图3 混合大邻域算法伪代码Fig.3 Pseudo codes of HLNA

4 算例设计与求解

4.1 算例设计

为了测试本文提出模型和算法的有效性，本文以当前世界上最大的12个CVRP算例[25]为数据基础，按照动态程度δ分别为0.25、0.50和0.75构造36个大规模动态车辆路径问题标准算例，算例中相关参数设定如表1所示.

表1 36个DVRP算例中相关参数值Table 1 The parameters values of 36 DVRP instances

需要注意的是本文设计的标准算例中只考虑了新顾客出现，其主要原因是

(1)后三种动态事件与当前执行方案密切相关；

(2)后三种动态事件发生后，根据本文模型也均可以转化为CVRP问题，故在此设计的算例不影响测试本文算法的性能.

表1中设新顾客在整个配送周期中按标号升序方式均匀地出现.

4.2 算例求解

为了对比分析单独使用IMGR(参数α=0.70)和IMGR+HLNA(参数p=0.05)联合使用的效果，本文分别用该两种方式求解在4.1节设计的36大规模动态车辆路径问题的标准算例，求解环境：Studio Visual C++6.0；CPU为Inter(R)core(TM)Q9400，内存为4.0G，主频为2.66GHz，其求解质量如表2所示，求解总耗时如表3所示，需要注意的是，求解质量为求解路径长度与对应静态算例已知最优解的偏差.

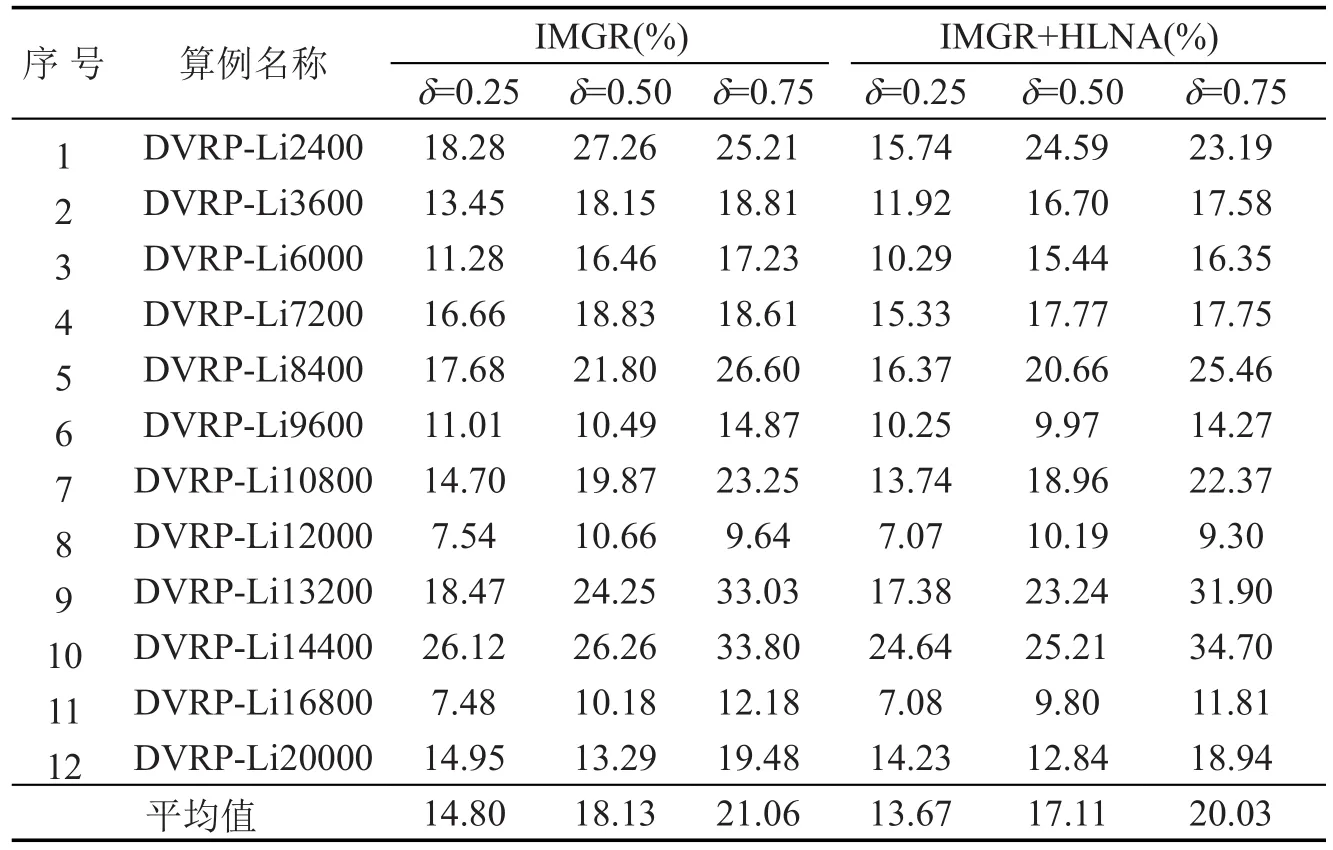
表2 IMGR与IMGR+HLNA求解36个算例质量Table 2 The solution quality comparison of IMGR and IMGR+HLNA

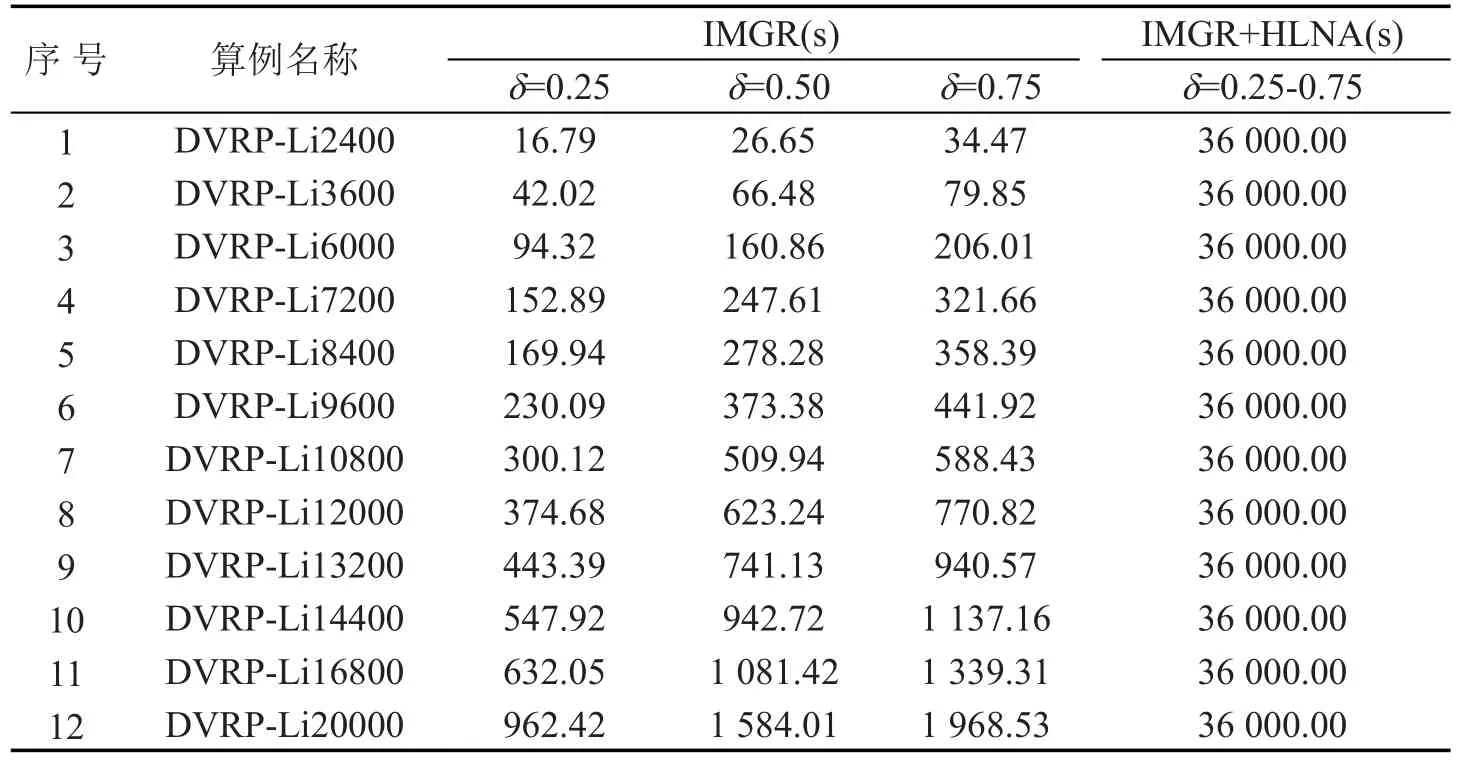
表3 IMGR和IMGR+HLNA求解36个算例总耗时Table 3 The total running time of IMGR and IMGR+HLNA

由求解结果可知，对于规模相同的算例，动态程度越大IMGR与IMGR+HLNA的求解质量会越差.并且相比较而言，IMGR+HLNA的求解质量要优于IMGR，通过对比表2所示的不同算例相邻动态事件间隔可以发现，动态事件发生的越频繁，IMGR+HLNA的求解质量优势越不明显，这是因为用于HLNA进一步改进的时间非常紧迫.

由上述求解质量结果可以得到以下启示：

(1)HLNA是元启发式算法，需要更充足的运行时间才能保证改进IMGR的求解结果，当运行时间非常有限时(不足60 s)，IMGR+HLNA与IMGR几乎有类似的求解结果.

(2)IMGR+HLNA在时间紧迫的情况下对于有些算例的求解质量甚至略低于IMGR(如DVRPLi14400动态程度δ=0.75时)，这说明在动态车辆路径算例中，当前更优的求解结果并不一定会导致最终形成的解质量更高.

由表3所示的IMGR和IMGR+HLNA的求解总时间可知，IMGR远远少于IMGR+HLNA的求解时间.这是因为IMGR+HLNA为了在动态事件未出现时，充分利用HLNA不断优化当前未执行的计划配送路线，使HLNA在整个配送周期T=10 h=36 000 s中一直处于运行状态.

总体来说，IMGR能够快速地应对动态事件，生成新的方案，且当动态事件出现非常频繁时IMGR与IMGR+HLNA有类似求解质量，但当动态事件出现时间间隔超过1 m in时，IMGR+HLNA求解质量明显优于IMGR.

5 研究结论

本文分析了DVRP问题中4种主要不同类型动态事件对优化问题本质的影响，通过分析得到DVRP问题可以转化为多个FSMOVRP问题，并进一步转化为CVRP问题，基于分析结论建立了DVRP模型.基于先完成后完善的思想，提出了一个由复杂度仅为O(n log n)的IMGR和HLNA构成的两阶段算法.为了验证本文提出的模型和算法的有效性，基于12个当前世界上最大的CVRP问题的标准算例，设计了36个DVRP算例，通过求解发现，本文提出的两阶段算法能够在合理时间内，求解动态程度较高的大规模的DVRP问题.

[1]Dantzig G B,Ramser J H.The truck dispatching problem[J].Management Science,1959,6(1):80-91.

[2]Psaraftis H N.Dynamic vehicle routing problems[M]. North-Holland:Elsevier,1988.

[3]Psaraftis H N.Dynamic vehicle routing:Status and prospects[J].Annal of Operations Research,1995,61 (1):143-164.

[4]Pillac V,Gendreau M,Guéret C,et al.A review of dynamic vehicle routing problems[J].European Journal of Operational Research,2013,225(1):1-11.

[5]Larsen A.The dynamic vehicle routing problem[D]. Technical University of Denmark,2001.

[6]Brotcorne L,Laporte G,Semet F.Ambulance location and relocation models[J].European Journal of Operational Research,2003,147(3):451-463.

[7]Taniguchi E,Shimamoto H.Intelligent transportation system based dynamic vehicle routing and scheduling with variable travel times[J].Transportation Research Part C:Emerging Technologies,2004,12(3-4):235-250.

[8]Fleischmann B,Gnutzmann S,Sandvoss E.Dynamic vehicle routing based on online traffic information[J]. Transportation Science,2004,38(4):420-433.

[9]Melachrinoudis E,Ilhan A B,Min H.A dial-a-ride problem for client transportation in a health-care organization[J].Computers& Operations Research, 2007,34(3):742-759.

[10]Khouadjia M R,Sarasola B,Alba E,et al.A comparative study between dynamic adapted PSO and VNS for the vehicle routing problem with dynamic requests[J]. Applied Soft Computing,2012,12(4):1426-1439.

[11]Ferrucci F,Bock S,Gendreau M.A pro-active real-time control approach for dynamic vehicle routing problems dealing with the delivery of urgent goods[J].European Journal of Operational Research,2013,225(1):130-141.

[12]Albareda-Sambola M,Fernández E,Laporte G.The dynamic multiperiod vehicle routing problem with probabilistic information[J].Computers&Operations Research,2014,48(2):31-39.

[13]Ghannadpour S F,Noori S,Tavakkoli-Moghaddam R, et al.A multi-objective dynamic vehicle routing problem with fuzzy time windows:Model,solution and application[J].Applied Soft Computing,2014,14 (1):504-527.

[14]谢秉磊,郭耀煌,郭强.动态车辆路径问题:现状与展望[J].系统工程理论方法应用,2002,11(2):116-120. [XIE B L,GUO Y H,GUO Q.Dynamic vehicle routing problems:status and prospect[J].Systems Engineering Theory Methodology Applications,2002,11(2):116-120.]

[15]郭耀煌,谢秉磊.一类随机动态车辆路径问题的策略分析[J].管理工程学报,2003,17(4):114-115.[GUO Y H,XIE B L.Policy analysis on a stochastic dynamic vehicle routing problem[J].Journal of Industrial Engineering Engineering Management,2003,17(4): 114-115.]

[16]郭耀煌,钟小鹏.动态车辆路径问题排队模型分析[J].管理科学学报,2006,9(1):33-37.[GUO Y H,ZHONG X P.Analysis of the queuing model of dynamic vehicle routing problem[J].Journal of Management Sciences in China,2006,9(1):33-37.]

[17]刘霞,齐欢.带时间窗的动态车辆路径问题的局部搜索算法[J].交通运输工程学报,2008,8(5):114-120. [LIU X,QI H.Local search algorithm of dynamic vehicle routing problem with time window[J].Journal of Traffic and Transportation Engineering,2008,8(5):114-120.]

[18]Hong L X.An improved LNS algorithm for real-time vehicle routing problem with time windows[J]. Computers&Operations Research,2012,39(2):151-163.

[19]陈久梅,张旭梅,肖剑,等.随机动态装卸混合问题的分区求解策略[J].管理科学学报,2012,15(1):43-53. [CHEN J M,ZHANG X M,XIAO J，et al.Region partitioning policy for stochastic dynamic pick-up and delivery problem[J].Journal of Management Sciences in China,2012,15(1):43-53.]

[20]葛显龙,王旭,邓蕾.基于联合配送的开放式动态车辆路径问题及算法研究[J].管理工程学报,2013,27 (03):60-68.[GE X L,WANG X,DENG L.Research on open and dynamic vehicle routing problems based on joint distribution[J].Journal of Industrial Engineering Management,2013,27(03):60-68.]

[21]Bentley J L.K-d trees for semidynamic point sets[C]// Proc.6th Ann.ACM Symp on Computational Geometry,1990:187-197.

[22]饶卫振,金淳.求解大规模CVRP问题的快速贪婪算法[J].管理工程学报,2014,28(02):45-54.[RAO W Z, JIN C.An efficient greedy heuristic for solving largescale capacitated vehicle routing problem[J].Journal of Industrial Engineering Management,2014,28(02):45-54.]

[23]Rao W Z,Jin C.A method for analyzing solution space of traveling salesman problem based on complex network[J].International Journal of Innovative Computing Information and Control,2013,9(9):3685-3700.

[24]Costa L D,Oliveira O N,Travieso G,et al.Analyzing and modeling real-world phenomena with complex networks:A survey of applications[J].Advances in Physics,2011,60(3):329-412.

[25]Li F Y,Golden B,Wasil E.Very large-scale vehicle routing:New test problems,algorithms,and results[J]. Computers&Operations Research,2005,32(5):1165-1179.

Model and Two-stage Algorithm on Dynamic Vehicle Routing Problem

RAO Wei-zhen1，JIN Chun2，LIU Feng3，YANG Lei1
(1.College of Economics and Management,Shandong University of Science and Technology,Qingdao 266590,Shandong, China;2.Institute of Systems and Engineering,Dalian University of Technology,Dalian 116024,Liaoning,China;3.College of Management Science and Engineering,Dongbei University of Finance and Economics,Dalian 116025,Liaoning,China)

In order to effectively solve dynamic vehicle routing problem(DVRP),this paper analyzes the substantial effect of four main categories of dynamic information on classical vehicle routing problem,and transform DVRP into multiple static fleet size and mixed open vehicle routing problems(FSMOVRP).And FSMOVRP could be further converted to multiple capacitated vehicle routing problems(CVRP).The model based on CVRP is built up for DVRP.After that a two-stage algorithm is proposed to solve DVRP model according to the analysis of DVRP characteristics.In the first stage,a fast construction algorithm with merely O(nlogn)complexity is proposed on the basis of delivery region cutting strategy by K-d trees method.In the second stage,a hybrid local search algorithm is designed by analysis of structural principal of algorithm’s solution searching space.Finally for the purpose of algorithm verification,we design and solve 36 DVRP instances generated from 12 large scale CVRP benchmark instances.The results demonstrate the effectiveness of the model and two-stage solving algorithm.

logistics engineering;two-stage algorithm;DVRP;K-d trees;algorithm searching solution space

1009-6744（2015）01-0159-08

：U491

：A

2014-08-08

：2014-09-23录用日期：2014-10-09

国家自然科学基金（71271041）；山东省优秀中青年科学家科研奖励基金（BS2014SF001）；山东科技大学人才引进基金（RCJJ2013020）；山东省软科学研究计划项目（2014RKB01506）.

饶卫振（1981-），男，江西丰城人，讲师. ＊

：raoweizhen@163.com