蒙特卡罗法在边坡可靠度分析中的应用

赵 清 静

(中国电建集团西北勘测设计研究院公司，陕西 西安 710065)

蒙特卡罗法在边坡可靠度分析中的应用

赵 清 静

(中国电建集团西北勘测设计研究院公司，陕西 西安 710065)

针对某均质边坡，采用简化Bishop法和Morgenstern-Price法计算滑动面的安全系数，对给定的滑动面进行了不同抽样次数的比较分析，选取了不同的土性随机参数进行计算，并进行了最大失效概率滑动面的搜索，得出了一些有意义的结论。

边坡稳定，可靠度分析，极限平衡法，失效概率

0 引言

边坡稳定分析是工程实践与设计中比较关键的工序。传统上而言，可使用确定的分析方法，也就是说将边坡稳定分析中的输入参数看成是确定的值，可采用的方法包括Simplified Bishop[1]、摩根斯坦法[2]、萨默尔法[3]、Unbalanced thrust force[4]，分析的结果为安全系数。虽然这种确定性的方法简单实用，但是事实上，由于构成边坡的土体材料在结构、组成以及应力历史条件等方面都表现出或强或弱的变异特性[5]，所以，这种确定性的分析方法无法真实地描述边坡的安全程度。边坡稳定可靠度分析是一种很有应用前景的分析方法，该法主要是基于统计学理论而形成的一种分析方法[6]。FOSM，RFEM，PM(如Rosenblueth法[7])，Monte Carlo Method等[8,9]。MCS(蒙特卡罗法)是一种随机抽样方法，并且该法受问题条件限制的影响较小，应用越来越广泛。本文采用蒙特卡罗法对一均质土坡进行了可靠度分析，重点研究了不同的MCS样本数目对失效概率以及土体材料参数的方差对失效概率的影响。此外，还比较了不同的样本数目下确定的滑动面与概率的滑动面之间的异同。

1 安全系数计算

对边坡进行稳定性分析或者是可靠度分析，必须要得到潜在滑动土体的稳定安全系数FS，对于不同形状的滑动土体，可采用的方法不同，例如：对于圆弧滑动，可以采用Simplified Bishop法计算安全系数；然而对于非圆弧滑动土体，则可使用摩根斯坦法计算得到其安全系数。关于计算安全系数的详细过程，限于篇幅，在此不再赘述，详情可参阅文献[10]。

2 蒙特卡罗方法

蒙特卡罗法，也就是随机抽样法或者统计试验法[8-11]。该法应用的前提是，必须要知道随机变量的概率密度函数。这种方法的主要思路如下：首先要对随机变量抽样，得到一系列的抽样值，然后利用极限状态函数来评价每个抽样值的结果，即在这个抽样值下判断边坡是否失稳。如果失稳，则称相应的抽样值为失效样本，失效样本的数目与总的样本的数目之比，可以作为失效概率的一种近似。下文主要对比分析了样本数目对计算结果的影响程度。

土体的强度参数中重度γ一般作为定值处理，而往往对粘聚力c和内摩擦角φ进行正态分布处理，也就是说，c的期望值μc以及标准差σc，内摩擦角φ的期望值μφ以及标准差σφ都是已知的。

3 算例分析

图1给出了一个典型的均质边坡，土体材料的密度ρ取为2 000 kg/m3，将其视为定值。考虑了μc以及σc三种情况，同样地，也考虑了μφ及σφ的三种组合，具体如表1所示。

表1 均质土坡计算参数

给出图2所示的一圆弧滑动面，其圆心坐标为：30.313,51.775；半径26.690，利用简化Bishop法计算得到的确定性安全系数为0.988，抽样次数取为50 000次，分别利用简化Bishop法和Morgenstern-Price法计算得到其失效概率为0.56和0.578。相对应的直方图分别如图3，图4所示。

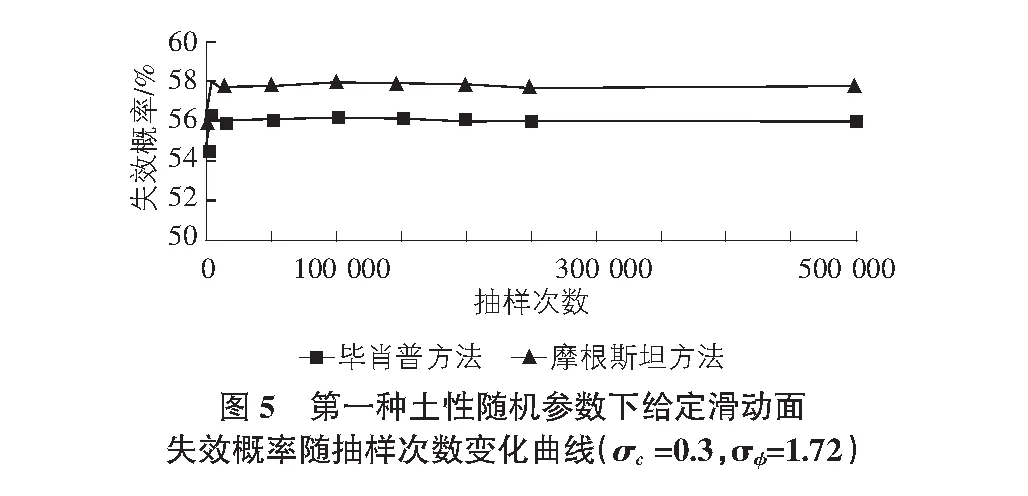
假定不同的抽样次数，分别采用简化Bishop法和Morgenstern-Price法进行了图2滑动面的失效概率计算，图5～图7给出了不同的土性随机参数的对应结果，如图7所示，在σc=0.3σφ=1.72时，Morgenstern-Price方法的结果均大于简化Bishop法结果，随着抽样次数的增加，失效概率先增大，然后至一定的抽样次数时，基本保持不变，此规律对于简化Bishop法和Morgenstern-Price法均适用。随着土性随机参数的变化，即标准差的增大，简化Bishop法和Morgenstern-Price法的结果趋于一致。

在边坡稳定确定性分析时，往往可以利用搜索算法寻求安全系数最小的滑动面作为设计的依据，在边坡可靠度分析时，同样需要寻找失效概率最大的滑动面作为设计依据，但需要注意的是，对于给定一个滑动面，确定性分析仅仅需要一次安全系数的计算，然而对于可靠度分析而言，利用蒙特卡罗法计算时，需要上万次的安全系数计算，因此搜索的效率就大大降低，确定分析仅需几秒钟，而可靠度分析却需要几天的时间。所以工程中经常利用确定性分析得到的最危险滑动面进行蒙特卡罗法的计算得到其失效概率作为设计的依据，为了探讨其区别，本文利用抽样次数为5 000和10 000两种数值进行了比对，其结果如图8，图9所示。其中完全搜索即代表可靠度分析得到的最大失效概率滑动面。由图可见，对于均质边坡而言，完全搜索得到的滑动面较之确定性搜索得到的滑动面略有不同，前者的滑动面出口位置偏右，入口位置也偏右。对于复杂边坡的情况，是下一步研究的重点。

4 结语

针对某均质边坡，采用简化Bishop法和Morgenstern-Price法计算滑动面的安全系数，首先对给定的滑动面进行了不同抽样次数的比较分析，其次选取了不同的土性随机参数进行计算，最后进行了最大失效概率滑动面的搜索，结果发现：随样本数目的增加，给定滑动土体的失效概率先增大，然后慢慢减小，最后稳定在某一数值；土性随机参数的标准差增大后，采用简化Bishop法和Morgenstern-Price法计算得到的失效概率逐渐接近；最大失效概率滑动面与最小安全系数滑动面不同。前者的入口和出口位置较之后者偏右。

[1] Bishop A W. The use of the slip circle in the stability analysis of slopes[J].Geotechnique,1955,5(1):7-17.

[2] Morgenstern N R, Price V E. The analysis of the stability of general slip surfaces [J].Geotechnique,1965,15(1):79-93.

[3] Sarma S K. Stability analysis of embankments and slopes[J].Geotechnique,1973,23(3):423-433.

[4] 时卫民，郑颖人，唐伯明，等.土坡稳定不平衡推力法的精度分析及其使用条件[J].岩土工程学报，2004，26(3)：313-317.

[5] 赵寿刚，兰 雁，沈细中，等.蒙特卡罗法在土质边坡可靠度分析中的应用[J].人民黄河，2006，28(5)：65-66.

[6] 袁 景，张秀丽.基于Monte-Carlo方法的边坡可靠度分析[J].辽宁工程技术大学学报，2005，24(sup)：10-13.

[7] 李 亮，褚雪松，郑榕明.Rosenblueth法在边坡可靠度分析中的应用[J].水利水电科技进展，2012,32(3)：53-56.

[8] 石 岩.蒙特卡罗模拟法在边坡可靠度分析中的应用[J].包钢科技，2001，27(1)：8-11.

[9] 李 亮，褚雪松，于广明.蒙特卡罗法在土质边坡失效概率计算中的应用[J].青岛理工大学学报，2012,33(6):6-10.

[10] 陈祖煜.土质边坡稳定分析——原理·方法·程序[M].北京：中国水利水电出版社，2003：372-373.

[11] 徐 江，杨更社，刘 慧.基于蒙特卡罗模拟法的冻土边坡可靠度评价[J].地下空间与工程学报，2007，3(8):1433-1437.

The application of Monte Carlo Method with traditional limit equilibrium methods in the reliability analysis of soil slopes

Zhao Qingjing

(XibeiEngineeringCorporationLimitedPowerChina,Xi’an710065,China)

For given homogenous slope, Simplified Bishop method and Morgenstern-Price method were used to calculate failure probability for given slip surface. The different sample numbers and different standard deviation values were assumed for the reliability analysis of the homogeneous slope. The critical probability slip surface with maximum failure probability was determined and was compared with that with minimum factor of safety. It draws some meaningful conclusions.

slope stability, reliability analysis, limit equilibrium method, failure probability

1009-6825(2015)16-0036-03

2015-03-28

赵清静(1979- )，女，高级工程师

TU413.62

A