沪深300股票指数期权定价实证研究

席 爽, 朱家明

(安徽财经大学 1.金融学院； 2.统计与应用数学学院， 安徽 蚌埠 233000)

沪深300股票指数期权定价实证研究

席 爽1, 朱家明2

(安徽财经大学 1.金融学院； 2.统计与应用数学学院， 安徽 蚌埠 233000)

针对中国尚未推出的沪深300股票指数期权，利用广义自回归条件异方差法和鞅方法等，使用EVIEWS软件，通过构建历史波动率模型和GARCH模型估计出标的指数的波动率水平，再利用通过鞅方法推导出的考虑股息率的扩展Black-Scholes期权定价模型对沪深300指数期权进行实证研究，计算出不同波动率水平下定期支付红利的欧式期权的理论价格。

沪深300股指期权； GARCH模型； Black-Scholes期权定价模型； 鞅方法

随着我国资本市场系统性风险的加大，投资者需要利用金融衍生产品进行风险管理，实现金融市场的资源配置和投资组合的优化。2015年2月9日，国内首支股票期权—华夏上证50ETF期权正式推出，开启了中国证券市场的期权时代。为了进一步推进金融市场创新发展和提高投资者利用金融衍生产品规避现货市场价格风险的能力，沪深300股指期权的推出指日可待。

股指期权市场发展的基础是能够对标的指数期权进行合理定价。Fischer Black和Myron Scholes(1973)[1]提出了布莱克-舒尔斯-默顿期权定价模型，即著名的Black-Scholes公式(简称B-S公式)并由此获得了诺贝尔经济学奖，它是期权定价理论的基石，主要针对不考虑支付红利情况下的欧式期权定价。为了很好的解决美式期权的定价问题，Cox，Ross和Rubinstein[2]于1979年提出了二叉树期权定价模型，相比Black-Scholes公式该模型更直观形象。Hull和White(1987)[3]通过Monte Carlo以级数的形式对期权进行了定价。股息作为广大投资者参与衍生产品市场获得收益的重要组成部分在经典的B-S模型中并未考虑，因此与现实情况不符。本文通过鞅方法推导考虑定期支付红利情况下的扩展B-S模型，然后采用扩展的B-S模型对沪深300股指欧式期权定价。

扩展的B-S定价模型中期权的价格取决于以下因素：标的指数当前市场价格S、未来T时刻执行价格K、市场无风险利率r、期权到期期限(T-t)、标的指数价格波动率σ以及定期支付红利的连续复利股息率δ。通过对各个指标的估计和计算，最终得到不同波动率水平下的欧式期权理论价格。

一、沪深300股指期权波动率估计

(一)研究思路

标的指数波动率是进行金融市场风险管理的重要参考指标，对股指价格波动率估计的精确程度决定了期权价格的精确性。本文采用历史波动率模型和GARCH模型进行标的指数波动率估计。

(二)历史波动率估计

本文选取的数据为2013年1月4日至2015年4月7日的沪深300指数的日收盘价，共计544个交易数据，数据来源为新浪财经。波动率的计算方法为：

{Pt}为标的股指的价格序列，T为样本容量，Rt为标的指数的对数收益率，σ为标的指数日波动率。

如图1所示，标的指数价格序列是非平稳的，为了得到平稳的时间序列，将标的指数价格进行对数差分处理，得到如图2所示的标的指数收益率序列。

图1 收盘价序列

图2 收益率序列

使用EVIEWS8软件得到标的指数收益率序列的统计特征如图3。

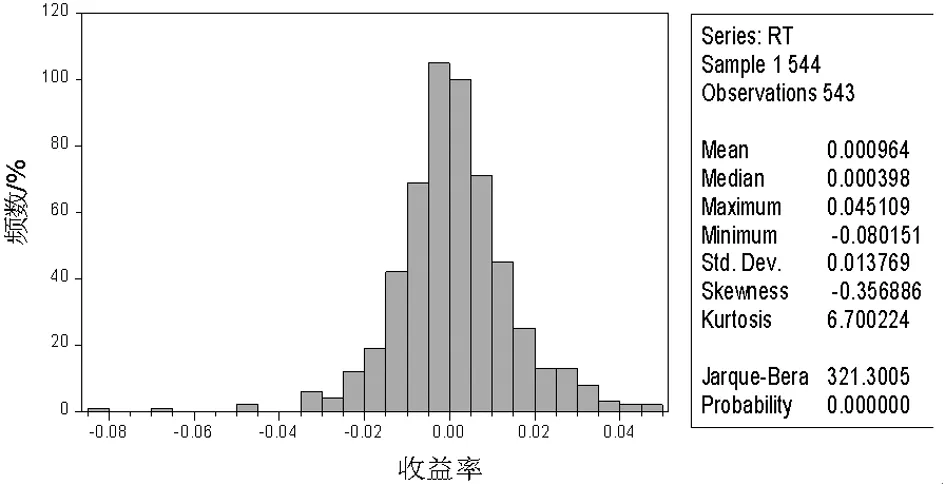
图3 对数收益率序列统计描述

得到标的指数的历史日波动率为0.013769。将日波动率转换成相应的年波动率，计算方法为：

假设我国股票市场年交易日天数为240天，则可以计算沪深300指数历史年波动率σ=0.013769×√240=0.213308=21.331%

(三)GARCH波动率估计

1.GARCH(1,1)模型

Bollerslev(1986)[4]提出了广义自回归条件异方差模型，即GARCH模型。GARCH模型[5]是用若干个协方差的滞后项代替随机干扰项的高阶滞后项，把条件方差转变为ARMA过程。它能够追踪随时间变化而改变的方差，消除残差序列的波动聚集性。GARCH(p,q)表示为：

(1)

(2)

GARCH过程为宽平稳过程的前提条件为：

ai反映当前信息对标的指数收益率序列波动的影响程度，βi反映过去信息对现在标的指数收益率序列波动的影响范围。VL表示长期平均方差。

dV=a(VL-V)dt+ζVdz

γ+α+β=1

2.数据处理

首先对标的指数收益率序列Rt使用最小二乘法进行估计，结果如下：

Rt=0.03961Rt-1+εt

图4 收益率序列残差图

对应标的指数收益率序列的残差图如图4所示。收益率序列可能存在异方差性，因此对标的指数收益率的残差序列进行波动聚集性检验。

表1 ARCH-LM检验

检验结果P值接近于0，表明残差序列存在显著的ARCH效应，拒绝其为同方差的原假设，因此可以使用GARCH(1,1)模型来描述这种异方差现象。

使用EVIEWS8对GARCH模型建立参数估计模型，结果如下：

均值方程：Rt=0.000717+0.0396944×Rt-1+εt

(3)

图5 GARCH(1,1)的建模估计

通过GARCH模型的条件方差方程(式(3))计算沪深300指数序列的长期方差VL：

股票指数的长期日波动率σ=√0.00214587=0.014648777

则沪深300股指相应年波动率为σ年=0.01465×√240=0.226937876=22.694%

二、期权定价实证

(一)扩展B-S模型推导

经典B-S模型是基于风险中性的定价原理，使用该模型对股指期权进行定价有五个假设条件，分别为：标的指数变化服从自然对数正态分布；在标的指数期权合约期内没有红利支付；金融市场没有相关交易成本；证券市场上允许对标的指数进行做空交易；证券市场上无风险套利机会不存在，股指的预期收益率是无风险利率r且在一定时间段内是固定不变的。

经典Black-Scholes模型为：

欧式看涨期权的价格为：c=S0N(d1)-Ke-r(T-t)N(d2)

欧式看跌期权的价格为：p=Ke-r(T-t)N(-d2)-S0N(-d1)

下面利用鞅方法以欧式看涨期权为例推导考虑定期支付股息的扩展B-S模型。

首先假定标的指数价格的变化过程服从几何布朗运动和伊藤过程：

dS=μSdS+σSdz

令F=lnS，则F遵循的随机过程为：

未来T时刻标的指数的对数价格服从正态分布：

标的指数欧式看涨期权的价格c为：

可以看出W服从标准正态分布W～N(0,1)

定义f(ST)为ST的密度函数，h(W)为W的密度函数，则:

(4)

同理可得欧式看跌期权的价格为：p=Ke-r(T-t)N(-d2)-Se-δ(T-t)N(-d1)

(5)

(二)数据处理

由于选取的是2013年1月4日至2015年4月7日的数据，则沪深300股指的市场价格S为2015年4月7日的股指收盘价S=4260.044。无风险利率采用上海银行间同业拆放利率(SHIBOR)，选取的无风险利率为SHIBOR一年期4.78%。沪深300股指的股息率按照连续复利下的历史股息率6.21%，数据来源于wind数据库。假定标的指数的到期执行价格K=4150.00，上文估计得到的沪深300股指的历史波动率为21.331%，以GARCH方法估计的波动率为22.694%。

沪深300股指期权定价所需的参数全部得到，代入(4)(5)式的扩展B-S定价模型可计算出到期日为2015年4月30日的支付红利的欧式看涨和看跌期权价格。结果如表2所示：

表2 2015年4月7日挂盘的沪深300指数欧式期权价格(元)

将得到的理论期权价格与沪深300指数期权的模拟交易数据进行比较，发现使用扩展的B-S模型以GARCH波动率进行期权定价的精确程度更高。

三、结论

为了促进金融产品创新发展和提高投资者和风险管理者利用金融衍生产品进行投资决策与风险管理能力，中金所未来必定推出沪深300股指期权。有效的合约设计和交易制度是保证沪深300股指期权市场平稳健康运行的关键。期权合约设计的基础是对期权的合理定价，本文利用考虑定期支付红利的扩展B-S模型对沪深300指数欧式期权进行了定价，期望能够对我国期权产品的开发和设计有所帮助。对于其他期权品种如股指期货期权，国债期权等的定价更为复杂，需要金融领域更多的探索和研究。

[1]BlackF,ScholesM.ThePricingofOptionsandCorporateLiabilities[J].JournalofPoliticalEconomy，1973，81(3):637-659.

[2]JohnC.Cox,StephenARoss,MarkRubenstein.Optionpricing:ASimplifiedApproach[J].JournalofFinancialEconomics，1979(3)：229-263.

[3]Hull,White.ThePricingofOptionsonAssetswithStochasticVolatilities[J].ReviewofFinancialStudies,1987，42(2):281-300.

[4]Bollerslev,T.GeneralizedAutoregressiveConditionalHeterosledasticity[J].JournalofEconometrics,1986(31):310-326.

[5]高铁梅.计量经济分析方法与建模：EViews应用及实例[M].北京：清华大学出版社，2009.

Empirical Research on the CSI 300 Stock Index Options Pricing

XI Shuang1， ZHU Jia-ming2

(1.SchoolofFinance; 2.SchoolofStatisticsandAppliedMathematics,AnhuiUniversityofFinance&Economics,Bengbu,Anhui233000)

China has not yet launched the CSI 300 stock index options.Through the method of generalized auto-regressive conditional heteroscedasticity and martingale methods,and by using EVIEWS software,building historical volatility and GARCH estimate volatility level of the underlying index,and then using the extended Black-Scholes option pricing model derived by martingale method taking into account the dividend yield on the CSI 300 index options empirical research,this thesis calculates the different volatility levels under the regular payment of dividends of the European option price theory.

CSI 300 stock index options; GARCH model; Black-Scholes option pricing model; Martingale method

2015-05-03

国家自然科学基金“随机动力系统的非一致指数二分性及其数值模拟”(11301001)；安徽财经大学教研项目“数学建模竞赛引领大学生科研创新的研究”(acjyzd201429)；安徽财经大学金融学院大学生科研创新基金项目“关于中国房地产价格指数期货的设计与定价研究”(JRXY2015010)。

席 爽，1994年生，女，安徽砀山人，研究方向：金融工程；

F830.91

A

1671-9743(2015)07-0035-04

*通讯作者：朱家明，1973年生，男，安徽泗县人，副教授，硕士，研究方向：应用数学与数学建模。