BTT导弹地形跟踪/地形回避控制器设计方法

魏东辉，水尊师，徐 骋

（北京机电工程研究所，北京100074）

BTT导弹地形跟踪/地形回避控制器设计方法

魏东辉，水尊师，徐 骋

（北京机电工程研究所，北京100074）

针对倾斜转弯（BTT）导弹地形跟踪/地形回避控制任务，在弹体坐标系下建立了导弹的动力学数学模型，将滚转通道独立解耦，俯仰-偏航通道耦合设计；依据H∞混合灵敏度理论，设计了俯仰-偏航通道过载控制器和滚转通道滚转角控制器；通过六自由度非线性仿真，验证了设计方法的有效性。

倾斜转弯；地形跟踪/地形回避；H∞混合灵敏度

0 引言

巡航导弹射程远、飞行时间长，容易被敌方防御系统探测跟踪，进而实施拦截。超低空飞行能够降低导弹的被探测概率，增大敌方防御系统的拦截难度，从而大幅提升导弹的突防能力。通常情况下，巡航导弹采用基于BTT的地形跟踪/地形回避技术来实现超低空飞行。如何设计良好的地形跟踪/地形回避控制器是该技术的关键之一。

1 倾斜转弯导弹运动数学模型

1.1 问题描述

倾斜转弯(BTT)导弹在实现地形跟踪/地形回避(TF/TA)时存在纵侧向同时机动的飞行状态，BTT导弹侧向机动是通过滚转使主升力面迅速转到期望平面上实现的。而滚转角速度的存在，使导弹俯仰和偏航通道存在较强的运动学耦合、动力学耦合、气动耦合以及控制耦合。并且，当导弹做大倾斜的转弯，即γ>15°时，过大的倾斜角会使得纵向运动和侧向运动耦合增强[1]，在这种条件下，基于小偏差线化的三通道独立建模方法已失去其合理性。针对BTT导弹的这一特点，本节通过在弹体系下建立导弹的运动模型，解决上述问题。

1.2 弹体系下导弹运动数学模型推导

1.2.1重要假设

1）将导弹抽象为质量恒定的刚体；2）忽略重力的影响（在导引律中补偿），仅考虑推力和空气动力作用；3）导弹的攻角α、侧滑角 β均为小量；4）发动机推力P与弹体纵轴重合；5）忽略下洗延迟引起的附加俯仰、偏航力矩；6）将导弹的飞行速度ν视为常数。

1.2.2作用在导弹上的力和力矩

基于1.2.1中的假设，作用在导弹上的力投影到弹体系下的表达式为：

作用在弹体系三轴上的力矩表达式为：

1.2.3弹体系下导弹质心运动的动力学方程

哥氏定理用于描述绝对变化率与相对变化率间的关系，选取弹体坐标系为活动坐标系，据哥氏定理有：

将式（3）展开得：

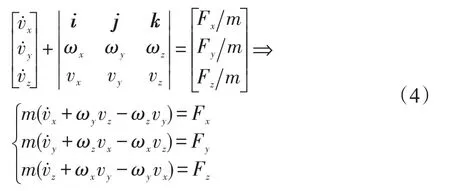
其中νχ,νy,νz是弹体系三轴上的速度分量。当α<15°,β<15°时，ν与νχ的差小于10%，故有下述近似成立：

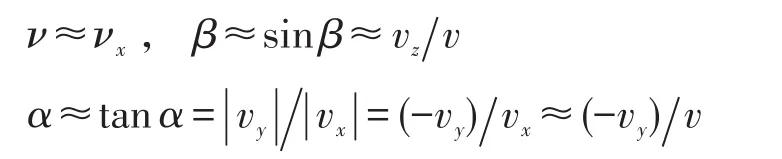
式中近似直接利用 α≈sinα≈(-vy)v对式（4）做如下变换：

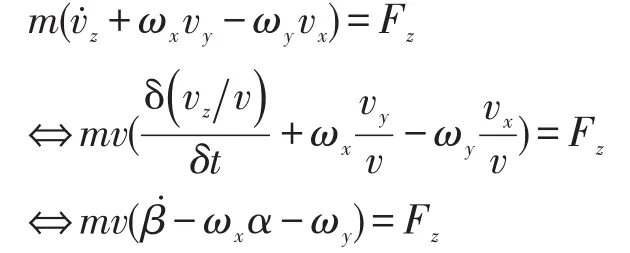
整理得

同理可得：

1.2.4弹体系下导弹绕质心转动的动力学方程

因为弹体所有的惯性积为零，且Iz=Iy，展开后的方程为[2]：

1.2.5舵机模型

舵机模型用如下一阶惯性环节近似

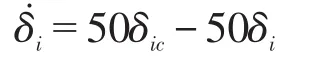
其中，δi为实际舵偏角，δic为舵偏角指令，俯仰、偏航、滚动舵均采用上述模型。

1.2.6导弹运动数学模型

将力、力矩表达式（1）、式（2）带入式（5）～式（7），并据动力系数定义[2]化简、整理，可得本文BTT导弹的运动数学模型如下：

1）俯仰-偏航通道：

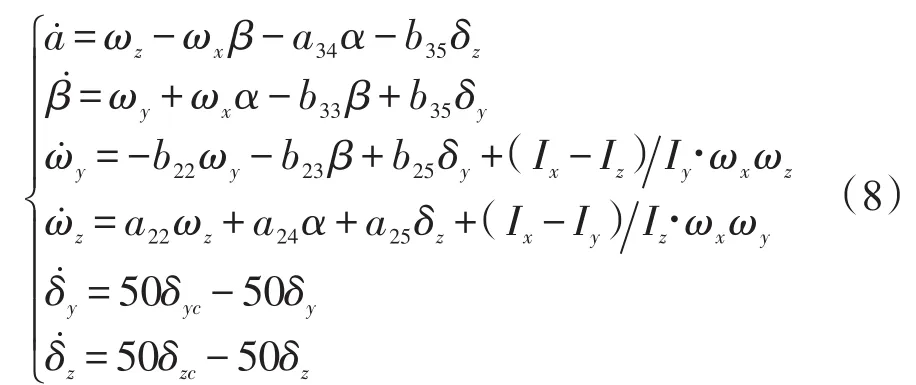
2）滚动通道:

由式（8）、式（9）可以看出，滚动通道可单独解耦，但俯仰-偏航通道存在耦合，且耦合强度与滚转角速度ωχ成正比。

1.2.7全状态可测的BTT导弹运动数学模型

对于俯仰-偏航通道，要精确测量模型的状态变量攻角α、侧滑角 β是比较困难的，从控制器设计的实用性角度考虑，加速度计可以方便地测出弹体系下的纵向和侧向过载nyt、nzt，因此可以用弹体系下的过载nyt和nzt来代替α和 β。将式（8）中的、、α、 β用、、nyt、nzt代替，可得俯仰-偏航通道的运动数学模型见式（10）。

至此，由式（9）和式（10）就组成了BTT导弹全状态可测的运动数学模型。

1.2.8 BTT导弹运动数学模型的状态空间描述

令式（10）中ωχ为常值1，将实际飞行中ωχ的变化视为模型的不确定性，利用所设计控制器的鲁棒性克服ωχ变化对闭环系统带来的影响，利用此方法便得到了BTT导弹的线性数学模型。其状态空间描述如下。

俯仰-偏航通道：状态变量，输出变量，控制量依次为：

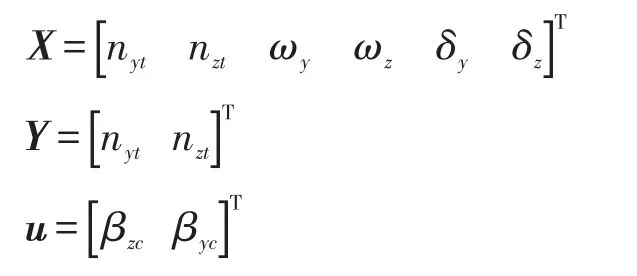
可见，俯仰-偏航通道为2入2出的多变量被控对象。

滚转通道：状态变量，输出变量，控制量依

次为：X=[ωχγ δχ]T，Y=γ,u=δχc。

2 混合灵敏度鲁棒控制器设计

2.1 问题描述

从上节BTT导弹的运动数学模型推导过程中可得出如下结论：导弹在进行侧向机动时存在一定的滚转角速度ωχ，从而导致俯仰-偏航通道存在较强耦合，并且耦合强度与滚转角速度ωχ的大小成正比。因此，我们希望设计的TF/TA控制器能够克服弹体滚转造成的严重耦合对弹体控制带来的影响，同时还希望它能克服气动参数变化、传感器噪声以及干扰力、干扰力矩等不确定性因素对导弹控制带来的影响。

鲁棒控制理论能有效解决被控对象不确定性问题，本节主要针对第一节中建立的俯仰-偏航通道2入2出过载数学模型和滚动通道数学模型，应用多变量系统鲁棒控制理论中的混合灵敏度设计方法，设计BTT导弹全状态控制器。

2.2 俯仰-偏航通道过载控制器设计

2.2.1控制回路结构设计

根据已建立的数学模型，设计俯仰-偏航通道的过载控制回路结构如下图所示：

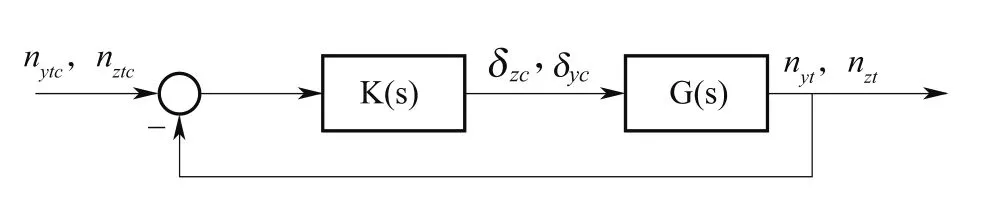
图1 俯仰-偏航通道过载控制回路框图Fig.1 Overload control loop structure for pitch-yaw channel

2.2.2权函数设计[3]

1）设计不确定性界函数W2(S)

补灵敏度函数T表示r到y的闭环传递函数，本文选择理想的Ti为一阶对角阵形式，这样可保证在阶跃指令输入下，闭环系统的输出无超调。设Ti=1(τs+1)I2×2，其单位阶跃响应为 y(t)=1-e-t/τ，在tr时刻，期望y(tr)要达到终值的m%，由此确定惯性时间常数为τ=-tr/1n(1-m%)。

本文针对被控对象的特点，选取tr=0.6，m=90，计算得τ=0.26，再根据带宽Wb与τ的反比关系取期望的闭环带宽Wb=4rad/s。

首先，令W2(s)=，其中选取k2<1。其次，利用Matlab工具箱设计H∞控制器时，需满足当 s→∞时W2(s)有界，所以要在分母上乘以τ1s+1，得

最后，通过调整参数k2、τ1以满足W2(s)的高通滤波性以及与0dB线交叉频率的要求。经调试，确定k2=0.6，τ1=0.0001。

2）设计性能权函数W1(s)

因为S+T=I，Ti=1(τs+1)I2×2，所以理想的灵敏 度 函 数 为 Si=s(s+1 τ)I2×2。 同 上 ， 令W1(s)=，其中k1<1，其次为满足W1(s)不同频段的幅值要求以及与0dB线交叉频率的要求，对W1(s)做如下修正，W1(s)=[k1(s+1 τ)](s+τ2)I2×2。经调试，确定k1=0.4，τ2=0.001。

2.2.3控制器求取

1）求取广义被控对象P(s)：由于求取H∞鲁棒控制器设计的算法定义在标准H∞控制问题框架下，所以欲求得控制器需首先求出广义被控对象P(s)[4]。

2）求解H∞控制器K(s)：利用Matlab鲁棒控制工具箱可以计算得到控制器K(s)。但直接利用上述方法得到的控制器为一个2×2的传递函数矩阵，且矩阵的每一个元素阶次高达14阶，由于过高的阶次实现起来比较困难，所以需要对求得的控制器K(s)进行降阶处理。降阶处理分三步完成，首先求K(s)的最小实现Km(s)，其次求Km(s)的均衡模型Kb(s)，最后求出降阶模型Kr(s)。

3）求K(s)的最小实现：对一个可实现的传递函数来说，有无穷多个状态空间实现与其对应，其中维数最小的状态空间实现称为该传递函数的最小实现[4]。

4）基于Gram矩阵的均衡降阶处理：基于Gram矩阵的均衡降阶方法的理论依据和均衡实现的基本思想可参见文献[5]。

至此，本文得到一个6阶的控制器Kr(s)

另外，控制器Kr(s)也可以用一个2入2出6状态的状态空间形式描述，其中2个输入为弹体系下纵、侧向过载指令与实际输出过载的差，2个输出为俯仰舵偏角和偏航舵偏角指令。

5）控制器离散化处理：考虑到后续非线性仿真的需要，现利用Matlab中的函数c2d，采用零阶保持器的方法，以5ms作为采样周期，对上述得到的控制器状态空间描述做离散化处理，得到一个2入2出6状态的离散控制器状态空间描述。

2.3 滚转通道控制器设计

滚转通道控制器设计方法同俯仰-偏航通道，这里不再赘述，仅给出滚转通道的权函数和控制器设计结果。

不确定性界函数

性能权函数

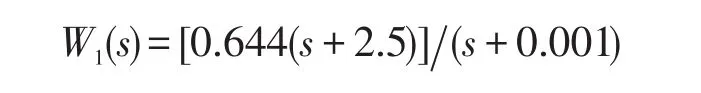
控制器

离散化后的控制器可用一个单入单出3状态的状态空间形式描述，输入为滚转角指令与实际滚转角输出的差，输出为副翼偏角指令。

2.4 线性仿真结果及分析

用设计好的离散控制器来控制名义被控对象，采样周期为5ms。纵向过载指令nytc=1，侧向过载指令nztc=0，滚转角指令γ=0.5rad，指令信号均为阶跃输入。

仿真结果表明，两通道都实现了对输入指令信号的渐进跟踪，且无超调，系统响应达到稳态值70%时的调节时间约为0.6s，满足快速性要求。

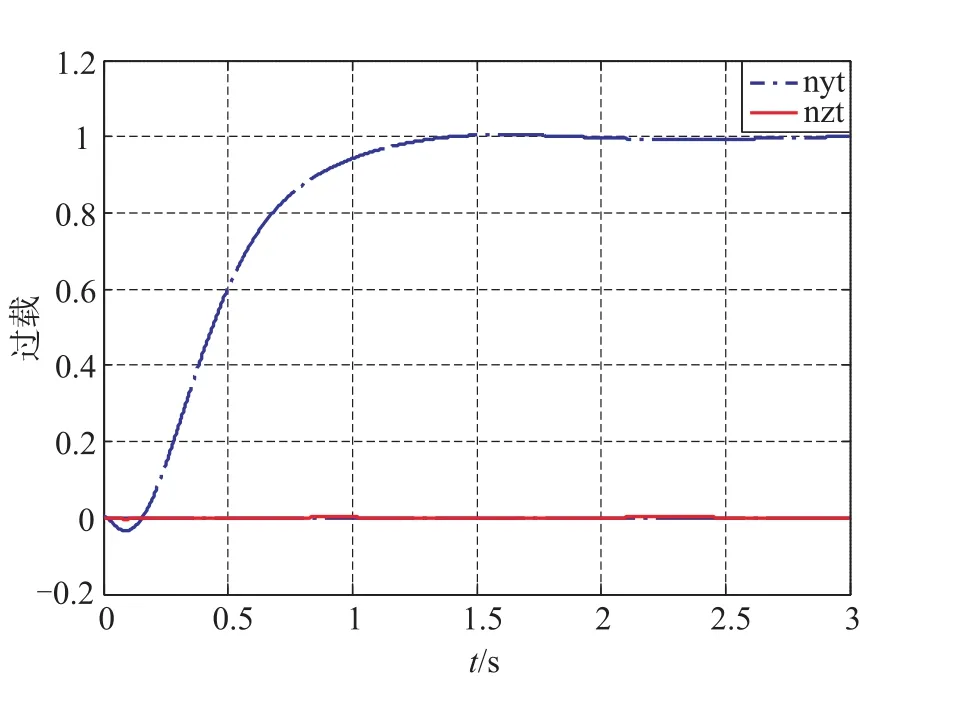
图2 俯仰-偏航通道过载阶跃响应曲线Fig.2 Overload step response curve for pitch-yaw channel

图3 滚转通道滚转角阶跃响应曲线Fig.3 Roll angle step response curve for roll channel

3 地形跟踪/地形回避制导指令设计

3.1 地形跟踪/地形回避制导策略简介

3.1.1适应角法

本文研究重点在于BTT导弹建模和TF/TA控制器设计，故关于TF/TA制导策略的研究，本文暂且引用一些参考文献的研究成果。基于适应角法的TF生成弹道倾角指令θFL，其具体形式为：θFL=K(λ+ϑ+HsR-Fs)。如图4所示：P点为前方地形最高点，Hs为安全偏置高度，R为导弹到P点的斜距，λ为雷达扫描角，ϑ为当前导弹的俯仰角，权函数K用来控制发挥导弹的机动能力，抑制函数Fs用来推迟拉起提高隐蔽性[5-8]。因此，实现对θFL指令的跟踪也就实现了TF飞行。类似地可以通过跟踪ψvFL指令实现TA飞行。

3.1.2 TF/TA制导控制回路设计

要实现跟踪期望弹道倾角θFL，可以通过控制弹道倾角θ或控制纵向过载ny来实现。由于控制过载较控制弹道倾角，相位上更加提前，另外通过对过载指令信号nyc限幅，可便于达到限制过载的目的。基于以上分析，本文采取通过控制纵向过载ny来实现TF飞行，TA飞行实现方法类似。

从弹道倾/偏角指令到弹道系下过载指令的转换关系如下（ay为弹道系下纵向加速度）：

其中， gcosθ为重力加速度补偿。同理nzc=k2vg(ψvFL-ψv)。经仿真调试 k1取2， k2取 0.7。制导控制回路结构如图5所示，其中第一步指令换算在本节已完成推导，第二步指令换算环节见本文3.2节。

图5 制导控制回路结构图Fig.5 The guidance and control loop structure

3.2 制导指令换算

欲利用本文设计的鲁棒控制器实现BTT导弹的TF/TA，需将本文3.1节中得到的弹道系下的纵侧向过载指令nyc、nzc，转换为弹体系下的纵侧向过载指令nytc、nztc以及滚转角指令。

1）将弹道系下过载指令转换到准弹体系下

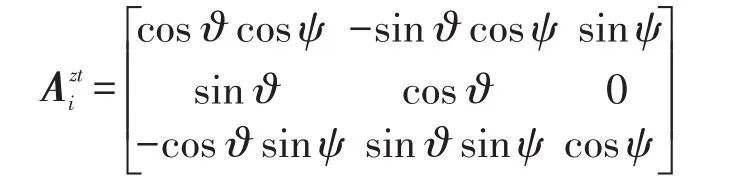
根据坐标转换矩阵的性质可得，由弹道系到准弹体系的坐标变化矩阵为：，则得：其中为准弹体系三轴上的指令过载分量。

2）将过载指令由准弹体系转换到弹体系下

根据准弹体系和弹体系的定义[3]可知，两者仅差一个滚转角γ，则弹体系下的过载指令和滚转角指令可表示为：

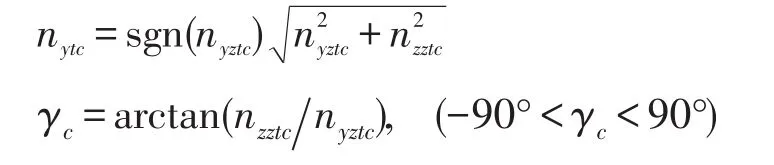
另外，为了实现较为理想的协调转弯，弹体系下侧向过载指令应为nzc=0。沿弹体纵轴过载的控制可以通过调节发动机油门来实现，本文不予考虑。至此，TF/TA指令已转换为弹体系下过载指令和滚转角指令。

4 六自由度非线性仿真

仿真时假定导弹保持恒速200m/s，仿真步长5ms，导弹起初为平飞状态，仿真时间t0=15s时，导弹接收正弦弹道倾角指令信号θpr=0.12sin[0.1π(t-t0)]，和斜坡弹道偏角指令ψvpr=0.02(t-t0)，ψvprmax=0.2，仿真飞行水平距离为10km。干扰力和干扰力矩 ΔFyt=500N,ΔFzt=200N，ΔMyt=500N·m,ΔMzt=200N·m，仿真结果见图6～图9，可以看出，所设计的TF/TA控制器能够控制导弹跟踪期望的弹道角指令，并能有效抑制干扰。

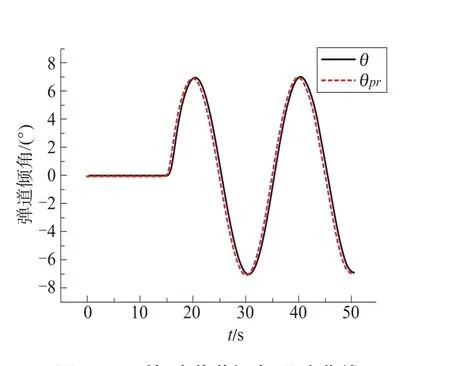
图6 无干扰时弹道倾角跟踪曲线Fig.6 The following curve of trajectory inclination angle in no disturbance

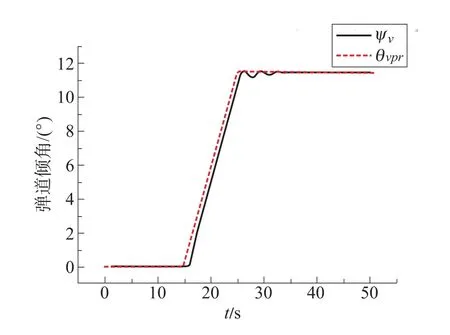
图7 无干扰时弹道偏角跟踪曲线Fig.7 The following curve of trajectory deflection angle in no disturbance

图8 有干扰时弹道倾角跟踪曲线Fig.8 The following curve of trajectory inclination angle in disturbance

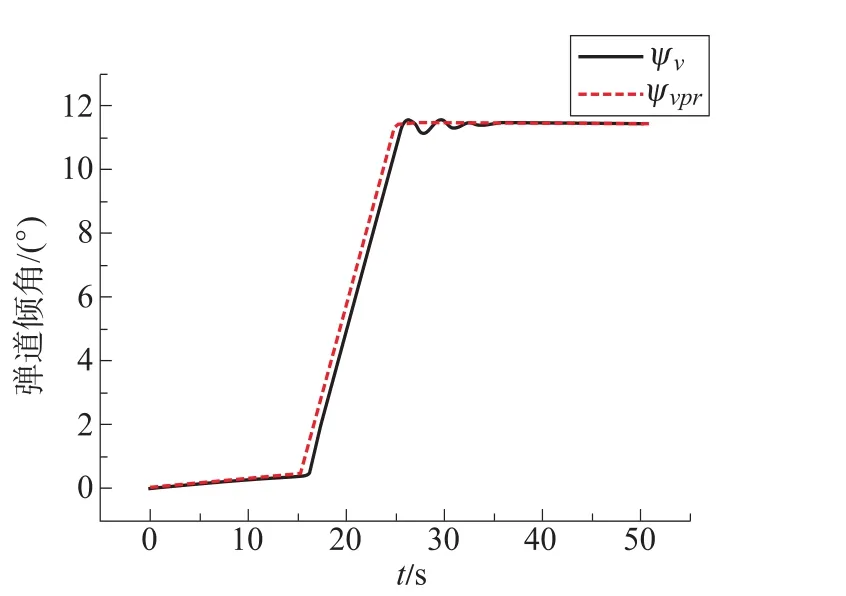
图9 有干扰时弹道偏角跟踪曲线Fig.9 The following curve of trajectory deflection angle in disturbance

5 结论

本文针对BTT导弹的特点，在弹体坐标系下建立了导弹的数学模型，实现了滚转通道独立解耦，俯仰-偏航通道耦合设计，并将俯仰—偏航通道转换为过载数学模型，以便于工程应用。基于已建立的模型，应用H∞混合灵敏度理论设计了俯仰-偏航通道的过载控制器和滚转通道的滚转角控制器。针对TF/TA适应角法给出的制导指令为弹道倾/偏角的情况，推导了将弹道倾/偏角指令转换为弹体系下纵侧向过载指令和滚转角指令的指令变换算法。最后，将设计的鲁棒控制器应用到TF/TA中，并通过6DOF非线性仿真验证了本文设计方法的有效性。

[1]周慧钟,李忠应,王瑾玫.有翼导弹飞行动力学[M].航空工业教材编审组.

[2]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2008.5.

[3]郑建华,杨涤.鲁棒控制理论在倾斜转弯导弹中的应用[M].北京:国防工业出版社,2001.4.

[4]杨琳,赵书强.H∞PSS设计中加权函数的选择及模型降阶[J].华北电力大学学报,2003,30:15-19.

[5]王长青,李景源.一类地形跟踪控制系统方案探讨[J].战术导弹技术.1998(2):35-39.

[6]姚宏浩.先进控制方法在TF/TA飞行控制系统中的应用[D].西安:西北工业大学硕士学位论文.2004.

[7]L U NARDI,H Y KAWANA.Development of Automatic Terrain-Following/Automatic Terrain-Avoidance Decoupling Techniques[C]//.AIAA,NO.75-1074.

[8]Gary Balas,Richard Chiang,Andy Packard.Robust Control Toolbox Getting Started Guide.

BTT Missile Controller DesignApproach forTerrain Following and TerrainAvoiding

WEI Dong-hui,SHUI Zun-shi,XU Cheng
（Beijing Electro-mechanical Engineering Institute，Beijing 100074，China）

For BTT missile terrain following and terrain avoiding requirements,the missile dynamic mathematical model is established in the body coordinates.The roll channel is decoupled from pitch-yaw channel.Based on H-infinite mixed sensitivity theory,overload controller for pitch-yaw channel and roll angle controller for roll channel are designed.Finally.The ndinear6-DOF simulation is performed to verify the validity of the method in this article.

Bank to turn;Terrain following/terrain avoiding;H-infinite mixed sensitivity

V24

A

2095-8110（2015）02-0013-07

2014-11-18；

2015-01-09。

魏东辉（1987-），男，硕士，主要从事飞行器导航、制导与控制方面的研究。E-mail:weidonghui2652@sina.com