指数函数膜计算模型的自动设计方法研究

赖正坤，孙 敏，杨昌东

(西南交通大学电气工程学院，四川 成都 610031)

指数函数膜计算模型的自动设计方法研究

赖正坤，孙 敏，杨昌东

(西南交通大学电气工程学院，四川 成都 610031)

膜计算模型设计是当前膜计算方向非常活跃的一个研究方向。研究者们利用数学、形式语言等工具进行膜计算基础理论研究，已经提出了各种膜计算模型，并取得了许多研究成果。从最开始复杂的手工推导到近期的自动设计研究，在膜计算模型自动设计方法变的日益成熟的过程中，膜计算模型也能解决更多的问题。在前人的基础上将膜计算自动设计方法用于推广到指数函数的计算，同时对设计方法进行了改进，采用置换编码的方法，结合遗传算法在P-Lingua仿真平台实现了2n、3n、4n的计算，验证此方法的有效性和可行性。

膜计算；指数函数；自动设计；置换编码

0 引 言

膜计算(membrane computing，MC)作为自然计算的一个年轻分支，旨在从生命细胞的结构与功能中以及从组织和器官等细胞群的协作中抽象出计算模型[1-3]，其计算模型被称为膜系统或P系统。膜计算领域的一个热门研究方向就是如何根据特定的任务要求，设计出可以完成一定功能的膜系统计算模型。研究者在研究的过程中，采用数学、形式语言等工具来进行膜计算的理论分析，已经提出了许多不同的细胞型计算模型[4-6]、组织型膜计算模型[7-8]、脉冲型膜计算模型[9]等。从最开始复杂的手工推导到近期的自动设计研究。随着对膜计算研究的不断深入，研究者们更多地把目光集中于对膜系统设计方法的研究。文献[10]第一次提出将遗传算法应用于膜系统的自动设计，在预先设计一个由18条规则组成的冗余规则集基础上，通过遗传算法对冗余规则集中的规则进行寻优，实现膜系统的自动设计；文献[11]将量子进化算法与膜系统的设计结合起来，并首次通过0、1编码来表示冗余规则集规则的选取，其中“0”表示不选取该条规则，“1”表示选取该条规则。不仅实现了计算42的膜系统设计，更是将问题扩展到了n2(n为自然数)膜系统的自动设计，且成功率要优于文献[10]；文献[12]首次提出了一种通过调整膜系统的膜结构、初始化对象集、进化规则集3个要素来实现完成特定计算任务的膜系统自动设计方法，并将该方法应用于42膜系统的自动设计中，实验表明，该方法能够成功设计出种类更多的膜系统；文献[13]在膜系统具有相同的初始化格局下，与量子进化算法相结合，分别实现了能够完成加、减、乘、除、加权5种算术运算膜系统的自动设计；文献[14]又提出了用膜系统自动设计来完成多项式的计算，能计算出最高次数为4次，最大项数为4项的多项式，同时改进了规则的设计，规则条数在预设最大数目内可以变化。

虽然上述文献成功地将进化算法和细胞型膜系统的设计结合起来，但是只能完成一些较为简单的任务，在计算复杂问题时成功率很低，因此在固定膜结构的前提下初始对象与规则通过自动设计来完成指数函数的计算，在推广膜计算的同时又能找到一些简单的P系统，同时最终用多个对象个数来表示结果，提高了试验的成功率，增加了膜系统的多样性和灵活性。

1 设计思想和设计方法

1.1 细胞型膜系统简介

细胞型膜系统是模仿细胞结构和功能的计算模型，一个细胞型膜系统主要由字母表、膜结构、初始化对象集、进化规则集、结果输出区域5个部分组成，如图1所示。其中，每一个组成元素均扮演着特定的角色，且能够与实际生物细胞中的组成要素相对应，对应关系及各自作用描述如下：

1) 字母表：对应实际生物细胞中的物质，是组成初始化对象集和进化规则集的字符集；

2) 膜结构：对应实际生物细胞的细胞膜及内膜之间组成的层次结构，用于划分不同对象的多重集所组成的区域。最外层膜被称为表层膜，膜内不包含其他膜的膜被称为基本膜。每个膜所围成的部分被称为区域，每个区域内包含着各自的规则与对象。

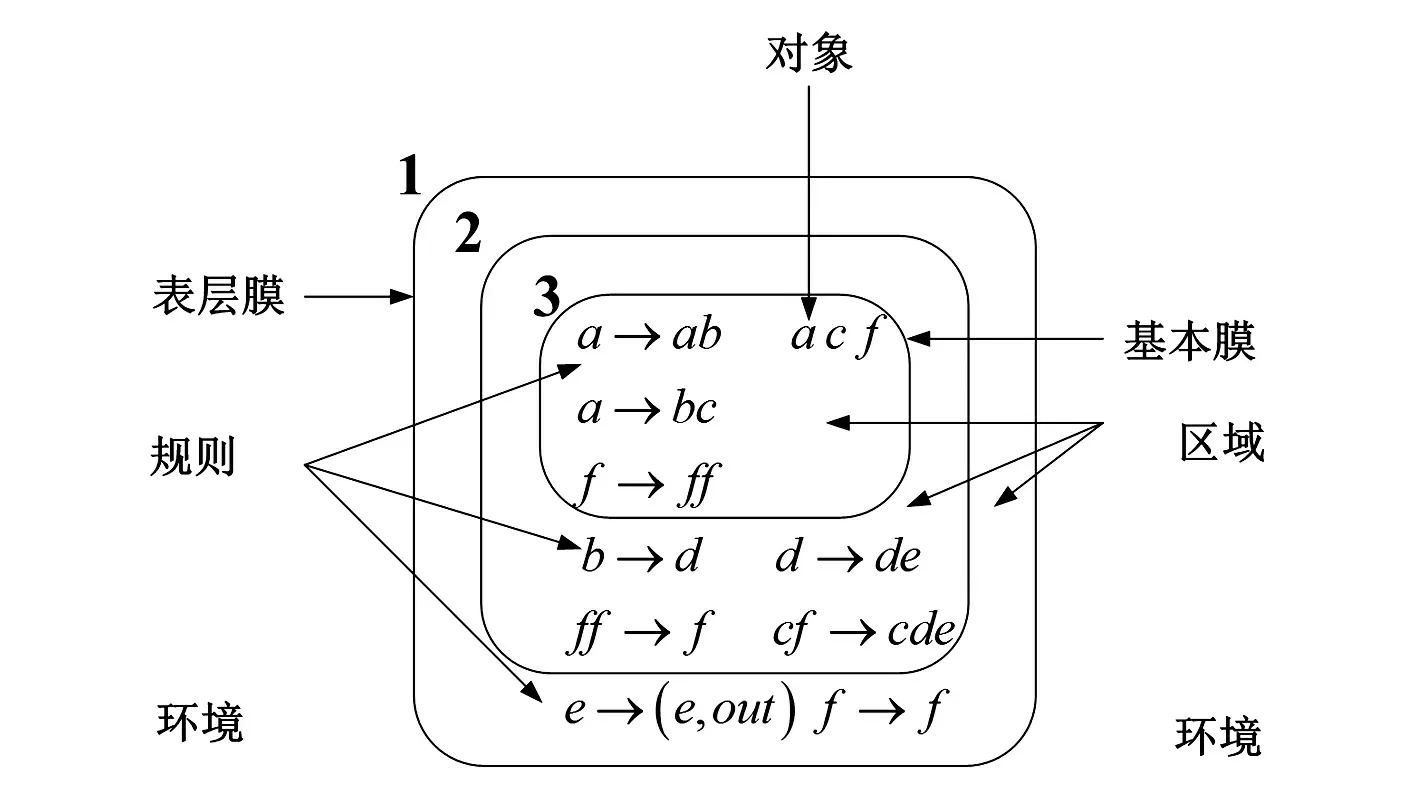
图1 膜系统示意图

3) 初始化对象集：对应实际生物细胞中的反应物，由字母表中的字符表示；

4) 进化规则集：犹如一个个的化学反应式，对应实际生物细胞膜中的化学反应。一条规则需要有一组输入物质，然后通过该条规则产生一组输出物质，每条规则能够确定被处理的对象以及具体进行的操作。规则间采用极大并行的方式执行，由字母表中的字符组成。

5) 结果输出区域：对应实际生物细胞中的环境，随着规则的执行，会不断有物质传递到环境中，每一次格局转换完成后，环境中的物质可当作是计算的“结果”。

1.2 设计思路和方法

设计目标：设计一个确定性的、非终止型的细胞型膜系统∏=(V，μ，W，R，i0)，使之能够用于求解简单的指数函数。

需要说明的是：1)由于给定的是确定性的目标，因此要设计的膜系统必须是确定性的膜系统，即在格局的变化中任何时刻每个对象只能触发执行一种规则；2)由于求解的目标是形如2n的指数函数，这就需要保证设计出的膜系统可以随着式中变量n取值的变化而计算出相应的结果，因此该膜系统必须是非终止型的，即在仿真过程中不会进入停机状态的膜系统，随着格局的变化总有规则被对象触发执行。

设计目标中要求设计出的膜系统能够对指数函数进行求解，这里可以将问题转化为寻找一种膜系统，在格局的变化过程中某一对象或多个对象个数的变化与函数结果随值的变化一致。这样可以将膜系统的设计问题当作是一个优化问题来处理，借助遗传算法，对膜系统的要素进行优化搜索，并通过膜系统仿真软件P-Lingua来验证、评价获得的膜系统个体，最终得到满意的膜系统。

考虑一个膜系统种群∏，∏={∏i}i⊆N(N为自然数集合)，则其中任意一个膜系统个体可定义为如下数学模型：

∏i=(V，μ，W，R，i0)

(1)

1)V是预先设计好的字母表，字母表中的元素称为对象，选自26个字母组成的英文字母表。设计时需根据初始化对象集中对象个数以及进化规则集中规则条数来合理确定字母表中对象的个数；

2)μ是膜结构，一般来讲，复杂的膜结构更能够实现设计难度更大的问题。而这里主要是对膜系统设计方法的研究，因此，用最为简单的单层膜结构μ=[]1反而更能证明所提方法的有效性；

3) 初始化对象集是W设计的目标，通过遗传算法对字母表寻优获得。设计时必须考虑初始化对象集中包含对象的最大个数；

4) 进化规则集R是设计的目标，通过遗传算法对字母表寻优获得；设计时必须考虑进化规则集中包含规则的最大条数；

5)io为输出结果区域，本方法中io=1，即最终结果保存到表层膜中。

1.3 膜系统的评价方法

适应度函数是膜系统设计中的关键，适应度函数设计的合理与否将直接关乎膜系统设计的成败。将多项式转化为与仿真步数step相关的函数f(step)，例如要设计一个求解2n的细胞型膜系统，则可以首先将其转化为关于仿真步数的函数f(step)，f(step)=2step；然后，以膜系统每一个格局的表层膜中某些对象的数量NumSomeObj来代表实际的计算结果，则适应度函数fitness可表示为

fitness=|NumSomeObj-f(step)|

(2)

fitness的值用于表征实际结果与期望结果之间的差距，显然，fitness的值越小越好。这里由于将函数中的变量n与仿真步数step相关联，因此被求解式中n需为自然数。

1.3 膜系统设计实现算法

这里的膜系统自动设计方法均是基于遗传算法实现的，因为是着眼于如何提出指数函数膜系统的设计方法，而不是如何设计进化算法，故而选用了现已发展成熟且具备专用算法包JGAP[15]的遗传算法来实现膜系统的自动设计，设计过程中只需考虑遗传操作算子的选择及遗传参数的设置问题。其中遗传算子采用精英选择算子、单点交叉算子、均匀变异算子，参数设置主要考虑以下一组参数。

set={Pm,Pc,Np,IterNum}

(3)

式中，Np是膜系统的种群规模；Pc是交叉概率；Pm是变异概率；Iternum是算法的最大迭代次数。

设计流程如图2所示。

步骤1：初始化膜系统种群∏={∏1，∏2，…，∏NP-1，∏NP}，其中NP为种群规模；

步骤2：判断当前仿真是否达到终止条件，“是”，则转向步骤6；“否”，则转向步骤3；

步骤3：单步仿真当前膜系统，即对个体解码后，创建该多项式膜系统的P-Lingua文件，调用内核P-LinguaCore中的函数实现对膜系统的仿真，并读取仿真结果；

步骤4：单步评价当前膜系统，即评价该多项式膜系统是否满足确定性、非终止性，是否含有冗余对象、冗余规则，是否能够用于对求解目标的计算等，若不满足期望要求，则对适应度函数增加相应的惩罚值；

图2 多项式膜系统自动设计流程

步骤5：经过评价后，若多项式膜系统最终的适应度函数值为0，则转向步骤6；若适应度函数值不为0，则转向步骤7；

步骤6：输出仿真结果，并转向步骤8；

步骤7：对种群进行选择、交叉、变异等更新操作，并转向步骤2；

步骤8：结束本次仿真。

2 膜系统三要素的置换编码

采用置换编码来编码膜系统。所谓置换编码就是采用字母表中每一个对象对应的实际位置来表示其编码。如字母表为V={s，a，b，c，x}，采用置换编码方案，则有下面给出的对应关系：s→1，a→2，b→3，x→4，c→5，且一个字母表中只需插入一个空字符λ，其对应的置换编码为0，即λ→0。那么选中字母表中每一个对象的概率为P(λ)=P(s)=P(a)=P(b)=P(x)=P(c)=1/6。而如果采用二进制编码方案，则需对字母表进行23-5=3位补空操作，即V′={λ，λ，λ，s，a，b，c，x}，那么选中对象s，a，b，c，x的概率为P(s)=P(a)=P(b)=P(x)=P(c)=1/8，而选中空字符λ的概率为P(λ)=3/8。

可以看出，相比于传统二进制编码，置换编码的优势在于在遗传算法对字母表进行寻优的过程中保证了每一个对象都是被等概率选取的，而等概率选取的好处最终体现在遗传优化的过程中不会产生过多无效的基因变化，如λ→λ。

由于已预先固定膜结构为单层膜结构μ=[]1，因此只需对膜系统的其余两要素初始化对象集W和进化规则集R进行编码，而W和R皆选自字母表V。

2.1 初始对象集W的置换编码

初始对象集表示为W={w1}，若已知w1中对象的最大个数为n，则初始化对象集可以用n位置换编码来表示。如w1中包含对象的最大个数为4，当w1=scax时，对应的4位置换编码为1524；当w1=ab时，对应的4位置换编码为0023。

2.2 进化规则集R的置换编码

进化规则集表示为R={R1}，进化规则采用重写规则，规则形式如下：

[leftobj→rightobj]1

(4)

假设每一条规则的左侧leftObjSet和右侧rightObjSet中包含对象的最大个数分别为nleft和nright，则可相应的采用nleft和nright位置换编码来分别表示leftObjSet和rightObjSet。那么R1中任何一条规则的置换编码位数可用公式(5)来计算。

Lr=nleft+nright

(5)

假设规则左侧最多包含1个对象，规则右侧最多包含5个对象，则每一条规则可以用6位置换编码来表示。如一条规则为r1=[s→assbc]1，则对应的置换编码为121135；若一条规则为r2=[x→abc]1，则对应的置换编码为400235。

设计过程中，还需知道R中包含的规则条数nR，即可用公式(6)来计算整个进化规则集的置换编码位数。

LR=nRLr

(6)

膜系统∏的置换编码：因为没有对膜结构进行编码，因此膜系统的编码只有初始化对象集和进化规则集两部分，编码的位数即为两部分编码位数之和，计算公式如下：

L∏=n+LR

(7)

3 仿真实验及结果分析

3.1 仿真实验

实验目标：设计一个能够用于求解2n的膜系统，其中n为自然数。这里将2n中变量n转化为仿真步数(step)，即随着仿真步数的增加就能计算出n依次增加的一系列2n的值。

实验条件：实验所用计算机为MD2.3GHZ，2GMB，仿真平台是Eclipse 3.5.0，JDK 版本为1.7.1，仿真膜系统的软件为P-Lingua 2.1.0。

参数设置：字母表V={s，a，b，x，c}；膜结构μ=[]1；初始对象集W={w1}，nw1=4；进化nR1=3nrleft=1nrright=4规则集R={R1}，规则均采用重写规则，计算结果以对象c的个数来表示；惩罚因子η=10 000，最大仿真步数MaxSteps=25。

遗传算法参数设置：根据文献[14]中可以看出：变异概率Pm=0.1时，成功率达到最高，平均进化代数最少；交叉概率Pc=0.75时，成功率和平均进化代数最为理想；当种群规模大于等于30时，成功率达到最大值，最大迭代次数Iternum=300时成功率最高，且平均运行时间最少。综上，可以得到一组最优的参数组合setBest={0.1，0.75，30，300}。

评价函数为fitness=|Numofc-2step|,即当c的个数满足2stetp(2n)时输出符合要求的膜系统。

3.2 仿真结果

在上述最优遗传参数组合的条件下，独立运行100次，其中有49次找到了成功的膜系统，将49个膜系统用膜系统分析软件[14]进行统计排除相同的膜系统，共得出14种不同的膜系统，由于其他要素都相同，所以下面只列出初始对象集和进化规则集，如表1所示。

得到上述结果后，采用P-Lingua软件中的膜系统仿真工具来展示膜系统每一步的格局变化，以验证所得的膜系统是否满足设计要求。这里以表1中的第5种膜系统的设计结果为例。仿真过程如图3和表2所示，图中则直观的展示了每一步规则执行完后各个对象的个数，表中所示为每一步由对象触发的规则，从膜系统的初始化格局开始，随着仿真的进行，规则被对象触发执行，膜系统的格局不断发生着变化。下面只展示了前几步中每一格局对象个数的变化，代表计算结果的对象c的个数也发生着变化，其值依次为2，4，8，16，32，64。不难看出，对象c的个数随仿真步数的变化规律与实验中所求的函数2n随变量n值的变化(n=1、n=2、n=3、n=4、n=5、n=6)的取值一致，也就证明了所设计的膜系统满足设计要求。

用同样的设计方法可以找到实现3n、4n的膜系统，验证了所提出的指数函数的膜系统自动设计方法的正确性和有效性。

表1 指数函数膜系统的设计结果

图3 膜系统格局转换示意图

执行的规则各对象的个数初始格局x,s第一步r1≡s→xcr2≡x→scas,c*2,a,x第二步r1≡s→xcr2≡s→scar3≡a→axss*2,c*4,x*2,a*2第三步r1≡s→xcr2≡s→scar3≡a→axss*4,c*8,x*4,a*4第四步r1≡s→xcr2≡s→scar3≡a→axss*8,c*16,x*8,a*8┆┆┆

[1] Paun Gh. Computing with Membranes[J]. Journal of Computer and System Sciences，2000, 61(1): 108-143 (frist circulated at TUCS Research Report No 208, November 1998).

[2] Paun Gh. Membrane Computing:An Introduction[M]. Berlin: Springer， 2002.

[3] 张葛祥, 潘林强. 自然计算的新分支——膜计算[J]. 计算机学报，2010, 2(33):208-214.

[4] Obtulowicz A, Paun Gh. (in search of)Probabilistic P Systems[J]. BioSystems, 2003, 70(2):107-121.

[5] Ferrettia C, Mauria G, Paun Gh, et al. On Three Variants of Rewriting P Systems[J]. Theoretical Computer Science, 2003, 301(1-3):201-215.

[6] Mutyam M. Rewriting P Systems:Improved Hierarchies[J].Theoretical Computer Science, 2005, 334(1-3):161-175.

[7] Freund R, Paun Gh. Tissue P Systems With Channel States[J]. Theoretical Computer Science, 2003, 296(2): 295-326.

[8] Martin-Vide C, Paun Gh, Pazos J. Tissue P system[J]. Theoretical Computer Science, 2003, 296(2):295-326.

[9] 潘林强，张兴义，曾湘祥，等. 脉冲神经膜计算系统的研究进展及展望[J]. 计算机学报, 2008,31(12):2090-2096.

[10] Escuela G, Gutiérrez M. An Application of Genetic Algorithms to Membrane Computing[C].Proc. of. the Eighth Brainstorming Week on Membrane Computing, Esvilla. 2010：101-108.

[11] Huang X, Zhang G, Rong H. Evolutionary Design of a Simple Membrane System[C].Lecture Notes in Computer Science. Berlin: Springer. 2012: 203-214.

[12] Ou Z, Zhang G, Wang T. Automatic Design of Cell-like P Systems through Tuning Membrane Structures, Initial Objects and Evolution Rules[J]. International Journal of Unconventional Computing, 2013.

[13] Chen Y, Zhang G, Wang T. Automatic Design of P Systems for Five Basic Arithmetic Operations within One Framework[J].Chinese Journal of Electronics, 23(CJE-2): 302-304.

[14] 孟琪.多项式膜计算模型的遗传优化设计方法[D].成都：西南交通大学,2014.

[15] Meffert K, Rotstan N, Knowles C, et al. Jgap-java Genetic Algorithms and Genetic Programming Package. URL:http://jgap. sf. net, 2008.

The design of membrane computing model is the current research direction of membrane computing. Researchers use math, formal language and other tools to form the basis for the theory of membrane computing, they have proposed a variety of membrane computing models and have achieved many research results. From the complex manual automatic derivation to the recent research of automatic design in membrane computing model, the automatic design methods becomes increasingly sophisticated, and the membrane computing model also can solve more problems. On the basis of the former researches, the automatic design methods of membrane computing are applied to the calculation of exponential function, while the design method is improved. Using replacement encoding method and combined with genetic algorithm in P-Lingua simulation platform to achieve 2n, 3n, 4ncalculations, the validity and feasibility of the proposed method are verified.

membrane computing; exponential function; automatic design; replacement encoding

TM769

A

1003-6954(2015)03-0050-05

2015-01-15)

赖正坤(1989)，硕士，研究方向为自然计算分支膜计算。