超特高压输电线路绕击性能分析

刘 意，文 艺

(国网四川检修公司，四川 成都 610072)

超特高压输电线路绕击性能分析

刘 意，文 艺

(国网四川检修公司，四川 成都 610072)

运用电气几何模型(EGM)的方法来分析超/特高压交流输电线路的绕击耐雷性能，并给出了计及导线工作电压的绕击耐雷水平和绕击跳闸率计算式。然后，再对影响超/特高压输电线路绕击耐雷特性的雷电流幅值、杆塔高度、线路绝缘水平，线路所经过的地形、保护角、工频瞬时电压、地面植被等主要因素做了分析研究。

超特高压；输电线路；耐雷性能；电气几何模型；绕击跳闸率

0 前 言

经验表明，不同电压等级的输电线路雷击跳闸的主要原因不同。500 kV及以上超/特高压输电线路，绕击占绝大部分[1]。分析超/特高压交流输电线路的耐雷性能，就要对其绕击耐雷性能展开分析。

超/特高压线路输送距离远，线路走廊所经区域地形复杂，大多穿越中国多雷区域，因此，需要综合考虑多方面因素对超/特高压线路绕击性能的影响。

1 雷电绕击分析方法

中国现今常用的输电线路绕击耐雷性能的分析方法有：规程法、电气几何模型(electric geometric model,EGM)、改进型电气几何模型、先导发展模型(leader progression model,LPM)等。目前广泛使用的EGM仍然有不足，这里提出了一种新的改进型EGM来分析超/特高压输电线路的绕击特性。

2 超/特高压输电线路EGM

在超/特高压交流输电线路的雷击跳闸事故中，绕击引起的雷击故障是主要因素。在运用EGM对输电线路绕击耐雷性能进行分析时，由于超/特高压杆塔很高，当较小的雷电流绕击导线时，大地雷电捕捉面离地高度低于导线在杆塔的悬挂高度，因此，绕击弧需要画到导线所在水平面以下。文献[2]还表明导线击距与雷电流、导线平均高度和导线工作电压有关。

在已有EGM基础上，给出了一个垂直地面落雷的杆塔线路EGM(水平地面)，如图1所示。图中，α为地线保护角；以过地线的垂线为基准逆时针为正，顺时针为负；θ1、θ2以水平线为基准，逆时针划过为正，顺时针划过为负；W为边相导线到杆塔中垂线的水平距离；hg、hc分别为地线和导线的平均对地高度；hs为大地雷电捕捉面离地高度；Rg、Rc为地线和导线的击距。图2所示EGM的基本原理与经典EGM类似，只不过这里考虑了导、地线以及大地对雷电先导吸引能力的区别，在分析导线上的击距时，还考虑了导线上的工作电压的影响。地线击距公式、大地雷电捕捉面离地高度公式如下。

地线击距[3]为

(1)

大地雷电捕捉面离地高度为[4]

hs=5.5I0.65

(2)

式中，I为雷电流幅值。

考虑导线工作电压时，按以下方法确定其击距计算式。长空气间隙的负极性放电电压跟不考虑工作电压时导线击距的关系如下[5]。

(3)

式中，Rc0为不考虑工作电压导线的击距；U0为雷电先导头部电压MV。

根据式(1)和式(3)可得

(4)

雷电对导线的击距公式如下：

(5)

式中，UPH为导线上工作电压的瞬时值,MV。

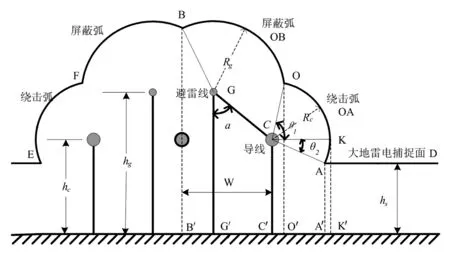
图1 完整杆塔线路的电气几何模型

由图1所示EGM可以看出，当雷电先导进入弧OB或弧FB上，雷电放电将击向地线，这样导线就被保护起来了，故称弧OB和弧FB为屏蔽弧；当雷电先导进入弧OA或弧FE上，则雷击击中导线，地线未起到应有的屏蔽作用，即发生了绕击现象，弧OA和弧FE称作绕击弧；若雷电先导落地大地雷电捕捉面上，那么雷电将对大地放电。

3 各因素对超/特高压输电线路绕击的影响

中国的防雷体系对线路走廊的雷电活动特征掌握不够全面，线路结构及地形地貌特征等还未能全面考虑，使得目前的防雷设计和措施改造还处于简单、粗放的状态，缺乏针对性[1]。因此，应该充分考虑线路工作电压、走廊雷电活动、线路绝缘配置、线路杆塔结构特性以及地形地貌等因素的影响，对输电线路的防雷进行综合评估[6]。

3.1 导线工频电压对绕击的影响

3.1.1 导线工频电压对绕击耐雷水平的影响

计及导线工频电压的绕击等效电路见图2。图中虚线右侧UPH=UPHmcos(wt+φ0)为从雷击点A看向被击交流线路的瞬时工作电压，Z/2为被击线路的等值波阻抗，Z为线路波阻抗；虚线左侧为从雷击点A看向雷电通道的电压源等效电路，U0分别代表沿雷电通道传播而来的电压波；Z0代表的是雷电通道的等值波阻抗。

从图2易得，雷击点A的电压表达式如式(6)：

(6)

在粗略计算式，近似有Z0≈Z/2成立。式(6)可简化为

(7)

绕击导线时，整个雷电放电过程的时间相对于工频电压变化的时间非常短，可认为雷击过程工作电压瞬时值不变，当雷击发生在工频电压位于任意初始相位φ0时，即存在

(8)

令Z=400Ω，UA=U50%，其中U50%为绝缘子串50%冲击放电电压。则计及导线工作电压时绕击耐雷水平[7]公式为

(9)

图2 线路绕击等效计算电路

3.1.2 导线工频电压对绕击跳闸率的影响

绕击要造成跳闸事故须满足两个条件，当绕击雷电流幅值I大于线路耐雷水平Imin时才会发生绝缘闪络现象，但绝缘闪络并不一定会造成跳闸，只有在冲击闪络转化为稳定的工频电弧才会引起线路跳闸。其中冲击闪络转化为稳定的工频电弧的概率称为建弧率η[8]。建弧率可由式(10)获得：

η=(4.5E0.75-14)×10-2

(10)

式中，E为绝缘子串的平均电场强度，可由式(11)求得：

(11)

式中，Un为线路运行额定电压；l为绝缘子串长度。

由图2中几何关系不难得出

(12)

(13)

那么，雷电流幅值I绕击概率Pα为

雷电流幅值概率是表征雷电活动频度，计算绕击跳闸率的另一重要参数。西南交通大学结合中国雷电流幅值概率分布，提出了一种适合中国实际情况的雷电流概率密度计算公式[9]。该雷电流概率密度PI的计算为

(15)

由式(15)和式(16)，可得绕击闪络率Pf为

(16)

因为雷电流幅值为Imax时，绕击弧变为0，θ1=θ2，联立式(12)和式(13)，并带入导、地线击距和大地雷电捕捉面高度可求得Imax。

绕击跳闸率n(次/km·a)的计算式如式(17)。

n=NPfη

(17)

式中，N为分析线路的年落雷次数。

3.2 雷电流对绕击的影响

雷电流有两方面含义：一是雷电流幅值的大小；二是雷电流幅值概率，其取值精确性直接关系到跳闸率的计算精度，进而也会对耐雷性能的分析产生影响。

3.2.1 雷电流幅值对绕击的影响

图3为雷击线路的EGM。较大幅值的雷电流对应较大的击距，一系列逐渐变大的雷电流形成了逐渐向外的一系列定位曲面，图中阴影部分为各雷电流情况下的绕击区，绕击弧随着雷电流幅值的增大而逐渐减小。当雷电流幅值超过该线路的绕击耐雷水平Imin时，线路就会发生绕击闪络；当雷电流增大到Imax时绕击弧长变为0，此时雷电不是击中地线，就是击中大地，而不会再发生绕击。此时的雷电流幅值Imax称为该线路的最大临界绕击电流，对应的击距则是最大击距Rcm[10]。最大击距Rcm与杆塔上导、地线的平均高度、塔头结构以及地形等有关。考虑击距系数β时，水平地面的最大击距计算公式为

(18)

式中，F=β2-sin2α；G=F[(hg-hc)/cosα2]。

图3 雷击线路的电气几何模型

3.2.2 雷电流幅值概率对绕击的影响

每次雷击的雷电流幅值呈随机概率分布，通过分析大量实测的雷电流幅值，可得到雷电流的幅值概率分布曲线。数据表明：雷电流幅值概率分布具有很强的地域性，它主要和该地区的纬度、地形地貌、雷暴强度等因素有关。

国网武汉高压研究院对1 000kV特高压交流输变电示范工程沿线雷电分布特征和易闪络段开展了全面的分析得到了如图4所示的沿线路走廊雷电流幅值累积概率分布曲线和图5所示的雷电流自然分布概率曲线。

图4 雷电流幅值累积概率分布曲线

以“晋东南—南阳—荆门”1 000kV特高压交流输变电示范工程ZBS2杆塔为例，由式(9)可得计及导线工作电压时的最小耐雷水平Imin≈35.51kA，雷电流概率密度PI≈32%，即幅值超过绕击最小闪络电流35.51kA的雷电流概率约为32%。

图5 雷电流自然分布概率曲线

3.3 线路绝缘水平对绕击的影响

超/特高压输电线路的绝缘有两类：一类是导线与杆塔之间的绝缘子串；另一类则是导线跟杆塔之间或大地之间的空气间隙[10]。

输电线路的绝缘水平主要取决于线路和杆塔间绝缘子串的放电特性。一般来说，当绝缘子串串长一定，绝缘子串片数越多，线路绝缘水平就越强，绝缘子串50%冲击放电电压U50%就越高，线路的绕击跳闸率就越低，线路的耐雷水平就越高。为使线路保持一定的绝缘水平，在设计杆塔和导线布置形式时，应合理设置导线与杆塔或大地的空气间隙。

3.4 线路走廊地形对绕击的影响

从4种不同类型的地形状况，考虑超/特高压交流输电线路的绕击耐雷性能。平原下的绕击状况已在3.1节中做过相应分析，这里主要研究山坡、山顶、峡谷3种地形对绕击的影响。

3.4.1 山坡上输电线路绕击分析

山坡线路的绕击EGM如图6。θ为山坡的倾角。

图6 山坡线路EGM

绕击弧在山坡地面的投影长度计算式如式(19)。

(19)

式中，θ1y、θ1z、θ2都是倾角θ的函数。由图6可得

(20)

位于山坡的输电线路绕击率计算式为

(21)

位于山坡的右侧和左侧输电线路的最大击距Rmy和Rmz的计算式如式(22)。

(22)

式中，

(23)

(24)

由3.1节所述方法可以得到Imaxy、Imaxz。然后，可计算输电线路的右侧和左侧的绕击闪络率Pfy和Pfz以及总的绕击闪络率Pf。

(25)

Pf=Pfy+Pfz

(26)

其中，PI为雷电流概率密度；Imin为绕击闪络的临界电流，kA。

3.4.2 山顶上输电线路绕击分析

山顶线路的绕击EGM如图7。其中θy、θz分别为山体右侧和左侧的地面倾角。

绕击弧在山坡地面的投影长度计算式如式(27)。

(27)

图7 山顶线路EGM

θ2z位于山顶的输电线路，其EGM中θ1y、θ1z、θ2y、都是山体倾角θy或θz的函数，由图8可得

(28)

山顶输电线路绕击率计算式为

(29)

位于山顶的输电线路右侧与左侧最大击距Rmy和Rmz的计算公式为

(30)

式中，

(31)

(32)

求得输电线路右(左)侧最大绕击雷电流Imaxy(Imaxz)，再根据式(25)和式(26)就可得到通过山顶的输电线路的绕击闪络率。

3.4.3 峡谷上输电线路绕击分析

穿过峡谷输电线路的绕击EGM分析如图8所示。θy、θz分别为峡谷右侧和左侧的地面倾角。

图8 峡谷线路EGM

与位于山坡、山顶的输电线路情况一样，位于峡谷输电线路绕击弧与θ1y、θ2y、θ1z、θ2z有关。其绕击弧在地面投影长度计算式如式(33)。

(33)

式中，θ1y、θ1z、θ2y、θ2z也都是山体倾角θy或θz的函数，其中θ2y、θ2z的计算式与式(28)中的计算式一样。由图8中几何关系有

(34)

峡谷输电线路绕击率计算式为

(35)

穿越峡谷的输电线路右侧与左侧最大击距Rmy和Rmz的计算公式为

(36)

式中，Fy、Fz的计算式如式(37)，Gy、Gz的计算式与式(32)一致。

(37)

求得右侧和左侧最大绕击雷电流Imaxy、Imaxz，再根据式(25)和式(26)就可得到通过山顶的输电线路的绕击闪络率。

3.5 保护角对绕击的影响

线路保护角对输电线路绕击耐雷性能也有较大影响。当输电线路的保护角变小时，导线受到地线更强的屏蔽作用，输电线路的绕击跳闸率会降低[11]。固定塔型上的输电线路，由于导线的弧垂大于地线的弧垂，故输电线路在两基杆塔档距中央处有最小保护角，在塔头处有最大保护角，所以在评价保护角对超/特高压输电线路绕击特性的影响时，应选择塔头处的保护角来进行分析[12]。以特高压ZBS2线路杆塔为研究对象，分析同一雷电流幅值不同线路保护角下平原地区塔头处输电线路绕击EGM。

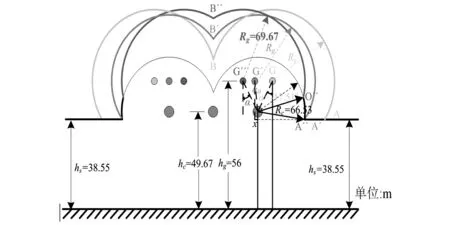
图9 不同保护角下酒杯塔线路EGM

图9为20kA雷电流下不同保护角时水平地面ZBS2塔型输电线路绕击EGM。通过逐渐缩短两根避雷线之间的距离以逐渐增大线路保护角α，对不同保护角下输电线路绕击跳闸率做定性分析。

结果显示：在20kA雷电流幅值作用前提下，地线位置从G移动到G″的过程中，当地线位于G处时，保护角α为负，导线不会发生导线绕击的情况；当地线位于G″处时，保护角α为正，这时可能会发生绕击导线的情况；当地线位于G′处时，并且当大于此保护角时，导线不再得到地线的有效屏蔽保护，小于此保护角时导线始终处于地线的有效保护下。称地线位于G′处的保护角α0为20kA雷电流幅值作用时的临界保护角，由图9得

(38)

临界保护角计算式为

(39)

3.6 地面植被对绕击的影响

国内关于地面植被对输电线路绕击跳闸率的影响的研究还很少，IEEE工作组在IEEEStd1410-2004中给出了树木对线路绕击跳闸率影响的标准，认为地面植被对线路的屏蔽作用随着树木高度以及树木与导线之间的水平距离的不同而存在较大差异[13]。地面植被影响下输电线路绕击跳闸率计算式为

N=n(1-Sf)

(40)

式中,N为考虑植被屏蔽后线路的绕击跳闸率；n为没有植被屏蔽作用的空旷地域中线路的绕击跳闸率；Sf为树木的屏蔽因素。

屏蔽因素Sf指线路周围的树木对单位线路绕击的屏蔽作用[14]。Sf值的确定现在还没有固定的公式，IEEEStd1410-2004给出了Sf随树木高度以及树木与导线间的水平距离而变化的曲线图10。

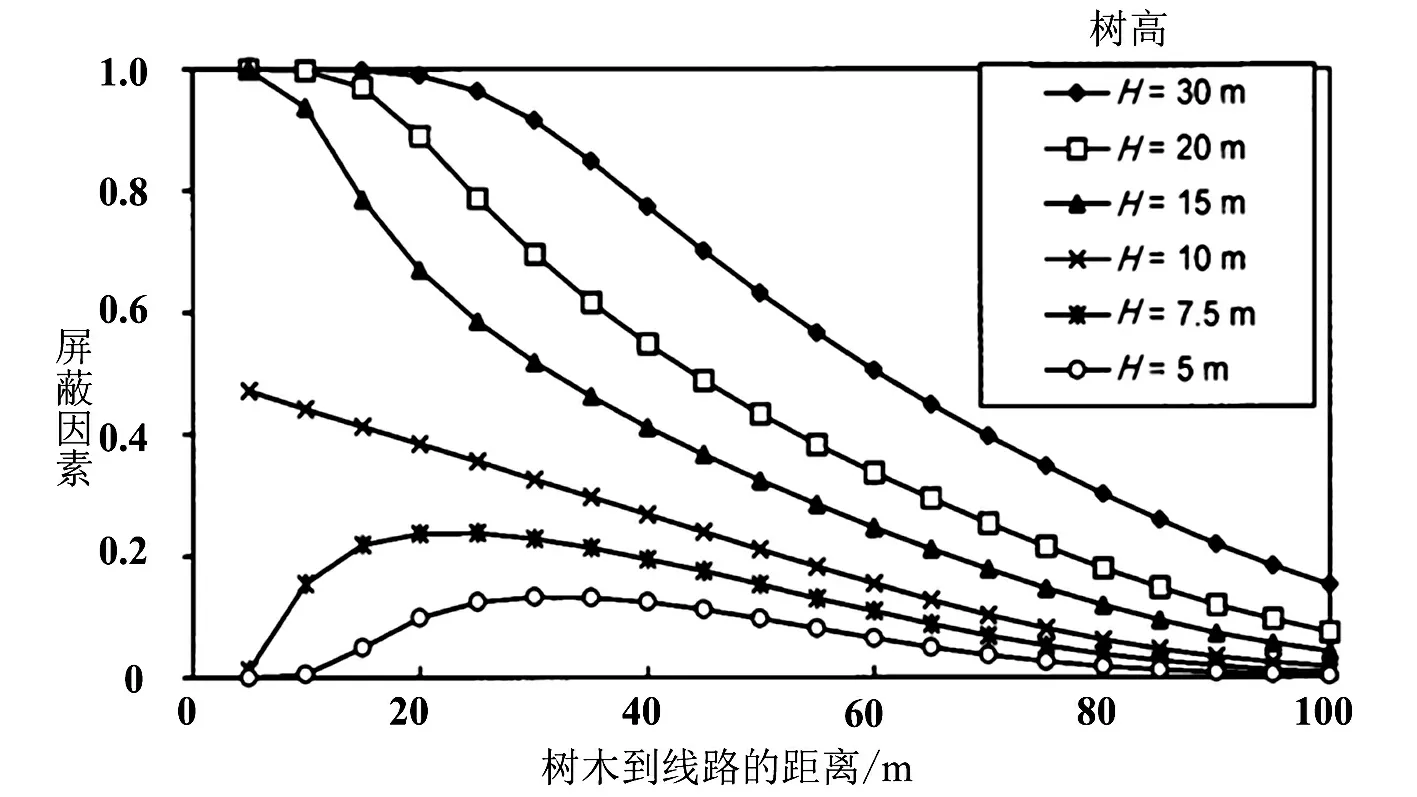
图10 不同树高、线路到树水平距离时的屏蔽因数

线路周围树木对线路绕击跳闸率的影响很大，在导线平均高度、树木与导线间水平距离不变的情况下，树木对线路的屏蔽作用随着树木高度的增加而增强，树木高度越高绕击跳闸率越小；在树高不变，树木与导线间水平距离不变的情况下，树木对线路的屏蔽作用随导线平均高度的增大而变小；高度大于10m的树木，对线路的屏蔽作用随与输电线路水平距离变近而越强。

4 计算分析

这里以500kVZB1型酒杯塔为例，杆塔几何尺寸如图11所示。导线弧垂为12m，避雷线弧垂为9.5m，绝缘子串长度为5m，四川地区落雷密度取5 次/km2·a，绕击耐雷水平为17kA。

地面倾角θ=0°，导线工频电压相角φ=0°，忽略地面植被影响时，不同绝缘子片数下线路的绕击跳闸率如图12(a)；地面倾角θ=0°，导线工频电压相角φ=0°，绝缘子串片数为28片，忽略地面植被影响时，不同线路保护角下线路绕击跳闸率如图12(b)；导线工频电压相角φ=0°，绝缘子串片数为28片，忽略地面植被影响时，不同地面倾角下线路绕击跳闸率如图12(c)；导线工频电压相角φ=0°，绝缘子串片数为28片，不同地面倾角线路绕击跳闸率加权平均值下，不同树高、不同线树距离下线路绕击跳闸率如图12(d)。

图11 500 kV单回线路杆塔结构几何尺寸

图12 不同影响因素对500 kV单回线路绕击跳闸率的影响

图12是根据上述绕击跳闸率计算式所得500kVZB1型酒杯塔在不同影响条件下的绕击跳闸率。从图中可以看出：随着绝缘子串片数的增加线路绕击跳闸率降低；绕击跳闸率值随着保护角的增加逐渐增大，当保护角超过10°时，绕击跳闸率值增加幅度变大；线路绕击跳闸率随着地面坡度的增大呈非线性上升趋势；在导线平均高度、树到导线水平距离不变的情况下，树木越高，树线路绕击跳闸率越小，且树木与输电线路的水平距离越近时，线路绕击跳闸率越小。

5 总结及建议

运用EGM分析了垂直地面落雷条件下超/特高压交流输电线路的绕击性能，通过对影响其绕击性能的几个主要因素的分析，结果表明如下：

1)只有在绕击导线的雷电流幅值I满足：Imin

2)决定线路绝缘水平的绝缘子片数足够多、导线与杆塔间或大地间的空气间隙足够长时，不会发生因线路绝缘而产生的绕击故障；

3)线路经过山顶时，绕击跳闸率最大；经过山坡时次之；位于峡谷的线路绕击跳闸率最低；平原地区的线路绕击跳闸率也很低；

4)减小地线保护角，绕击跳闸率将明显降低；

5)地面植被对超/特高压输电线路绕击耐雷水平的影响，与树高以及树木到线路的水平距离等有关。

上述各绕击影响因素的分析结果是在仅考虑某一个变量条件下得到的，而实际运行线路中，各类影响因素需综合考虑，才能准确评价线路的绕击特性。

[1] 李景禄等.现代防雷技术[M]．北京：中国水利水电出版社， 2009．

[2] 何金良，赵杰，NAYELM，等.导线电压对电气几何模型的雷电击距的影响[J].南方电网技术，2007，1(1)：14-19.

[3]ErikssonA.J．AnImprovedElectrogeometricModelforTransmissionLineShieldingAnalysis[J].IEEETransactionsonPowerDelivery，1987，2(3)：871-88．

[4]IEEEStd1243-1997，IEEEGuideforImprovingtheLightningPerformanceofTransmissionLines[S]．

[5] 刘振亚．特高压电网[M]．北京：中国经济出版社，2005．

[6] 陈家宏，吕军，钱之银，等．输电线路差异化防雷技术与策略[J]．高电压技术，2009，35(12)：2891-2902．

[7] 贾磊，舒亮，郑士普，等．计及工频电压的输电线路耐雷水平的研究[J].高电压技术，2006，32(11)：111-114．

[8] 赵智大．高电压技术[M]．北京：中国电力出版社，1999．

[9] 李瑞芳，吴广宁，曹晓斌，等.雷电流幅值概率计算公式[J]．电工技术学报，2011，26(4)：161-167．

[10] 刘洪建，和伟，徐八林，等.导线电压对其雷电绕击耐雷性能的影响[J]．南方电网技术，2011，5(2)：72-75．

[11] 王志勇，余占清，李雨，等.减小地线保护角对改善线路防雷性能的效果[J].高电压技术，2011，37(3)：622-628．

[12] 王茂成，张治取，滕杰，等．1 000kV单回特高压交流输电线路的绕击防雷保护[J]．电网技术，2007，32(1)：155-159．

[13]IEEEStd1410-2004，IEEEGuideforImprovingtheLightningPerformanceofElectricalPowerOverheadDistributionLines[S]．

[14] 陈国庆．交流输电线路绕击仿真模型及同杆双回耐雷性能的研究[D]．重庆：重庆大学，2003．

Electro-geometric model (EGM) is used to analyze the lightning protection performance of shielding failure for UHV/EHV transmission lines, and the formula for calculating the lightning shielding failure withstand level and the shielding failure trip-out rate is given which considers the effects of conductor operation voltage. Then, the main factors which would impact the lightning shielding failure performance for UHV/EHV transmission lines are analyzed and studied, such as lightning current amplitude, tower height, insulation level of lines, landforms along the transmission line corridor, the protection angle of tower, power-frequency voltage and ground vegetation.

EHV/UHV; transmission line; lightning protection performance; electro-geometric model; shielding failure trip-out rate

TM863

A

1003-6954(2015)03-0015-08

2015-03-19)

刘 意(1982)，工学硕士，工程师，研究方向为高压输电线路运行状态监测与安全评价；

文 艺(1988)，男，工学硕士，研究方向为输变电设备状态监测与故障诊断。