用于夹层玻璃抗爆设计的W-R法*

张红 邓汉国 姚小虎 龙谦

(华南理工大学 土木与交通学院, 广东 广州 510640)

用于夹层玻璃抗爆设计的W-R法*

张红 邓汉国 姚小虎 龙谦

(华南理工大学 土木与交通学院, 广东 广州 510640)

夹层玻璃的抗爆设计有利于抵抗爆炸冲击波对人员的伤害.传统的抗爆设计p-i图法(p为超压,i为单位面积正冲量)未考虑爆炸负压段的影响,而负压段会显著影响夹层玻璃的动态响应.为此,文中采用有限元法就爆炸负压段对p-i图抗爆设计方法的影响进行了仿真,针对p-i图抗爆设计方法的不足,提出了抗爆设计的W-R法(W为炸药当量,R为爆炸距离).相比于p-i图,W-R图更具规律性和直观性,W-R公式形式更为简单,用于抗爆设计更具可行性.文中还定性分析了玻璃几何参数对夹层玻璃抗冲击性能的影响,以玻璃临界破坏为基准,得到了评估夹层玻璃抗爆性能的W-R经验公式,可为夹层玻璃抗爆设计提供指导.

夹层玻璃;抗爆;临界破坏;炸药当量;爆炸距离;有限元法

随着世界各地恐怖主义袭击和各种爆炸事件的不断发生,建筑玻璃的破坏研究成为了人们关注的热点.爆炸事故中,爆炸冲击波作用到建筑玻璃上,产生飞溅的玻璃碎片,这是造成人员伤亡的主要原因[1].鉴于此,研究及设计人员开始考虑使用抗爆玻璃来减小甚至消除爆炸冲击波对人的伤害[2].

很多研究者进行了玻璃幕墙的抗爆研究,高轩能等[3]应用弹性薄板振动理论研究框支承玻璃在爆炸冲击荷载下的动力响应,得到玻璃最大挠度与最大应力的计算公式以及安全距离的经验公式,但忽略了爆炸负压段以及玻璃横向尺寸的影响.在玻璃幕墙抗爆设计方面,p-i(p为超压,i为单位面积正冲量)曲线被广泛用于评估结构的损伤.Wei等[4]研究了爆炸冲击下点支承整块单层玻璃和夹层玻璃的失效破坏模式,得到相应的p-i曲线,并将其用于评判玻璃的抗冲击性能,但所得p-i曲线只在某固定玻璃尺寸下才适用.Zhang等[5]研究了几何参数(包括玻璃尺寸、PVB(聚乙烯醇缩丁醛)薄膜厚度、玻璃厚度)和边界条件对p-i曲线的影响,最终得出的经验公式可直接用于爆炸载荷作用下的夹层玻璃抗冲击能力评估.然而,该研究未考虑爆炸负压段的影响,破坏是以PVB破坏为基准,可能高估了玻璃幕墙的抗冲击性能,存在一定风险.Krauthammer等[6]认为爆炸负压段对玻璃板的影响不可忽略,爆炸冲击波作用下,玻璃板可能飞向建筑物内,也可能向着相反的方向脱开窗框.Jun等[7]采用薄板小挠度理论、大挠度理论以及有限元法对爆炸荷载下夹层玻璃的动态响应进行了分析,指出爆炸负压段的影响一般不可忽略.

文中考虑爆炸负压段可能产生的影响,在对p-i图法进行修正的基础上,提出了新的夹层玻璃抗爆设计方法——W-R法(W为炸药当量,R为爆炸距离)；通过分析玻璃尺寸参数对夹层玻璃抗冲击性能的影响,得到了以玻璃临界破坏为基准的评估夹层玻璃抗爆性能的W-R经验公式,以期为夹层玻璃抗爆设计提供指导.

1 夹层玻璃有限元模型材料参数选取

文中夹层玻璃有限元模型的建立依据Kranzer等[8]的试验,材料参数取值的合理性采用Kranzer试验和p-i图进行验证.

1.1 有限元模型及试验验证

根据Kranzer等[8]的试验,夹层玻璃长、宽分别为1.1 m和0.9 m,总厚度为7.52 mm(3 mm厚外层玻璃+1.52 mm厚PVB+3 mm厚内层玻璃),玻璃内外表面所粘结的橡胶垫宽50 mm、厚4 mm.文中采用序号为FX014的爆炸试验数据来验证夹层玻璃有限元模型材料参数选取的合理性,爆炸荷载如图1所示[8].爆炸冲击荷载均匀分布,由于边界条件、几何形状和所施荷载等具有对称性,有限元模型模拟计算采用1/4模型,局部细节如图2所示.约束外层密封橡胶上表面以及内层密封橡胶下表面所有节点的所有自由度,对称面则约束法向自由度.在玻璃厚度方向划分4个网格,在PVB胶片和橡胶层厚度方向划分2个网格,板平面划分为220×180个网格,单元均采用线性减缩积分.玻璃与PVB接触方式采用面面绑定接触,使用type6沙漏控制.

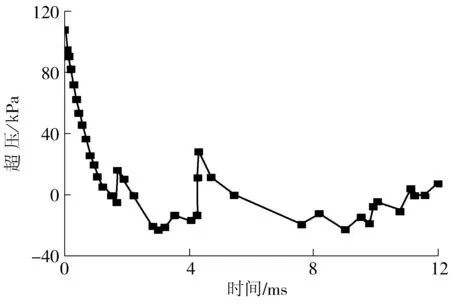
图1 试验FX014的超压-时间曲线[8]

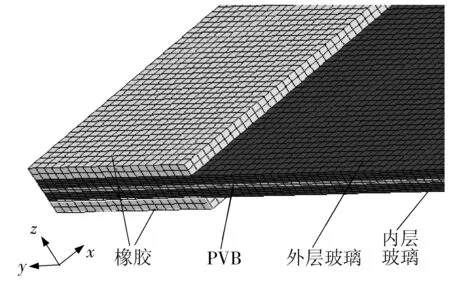
图2 1/4夹层玻璃模型

玻璃本构采用LS-DYNA中的110号材料JH2进行模拟,PVB、橡胶均取弹塑性本构.PVB、橡胶、玻璃[5,9- 10]的模型参数如表1和2所示.

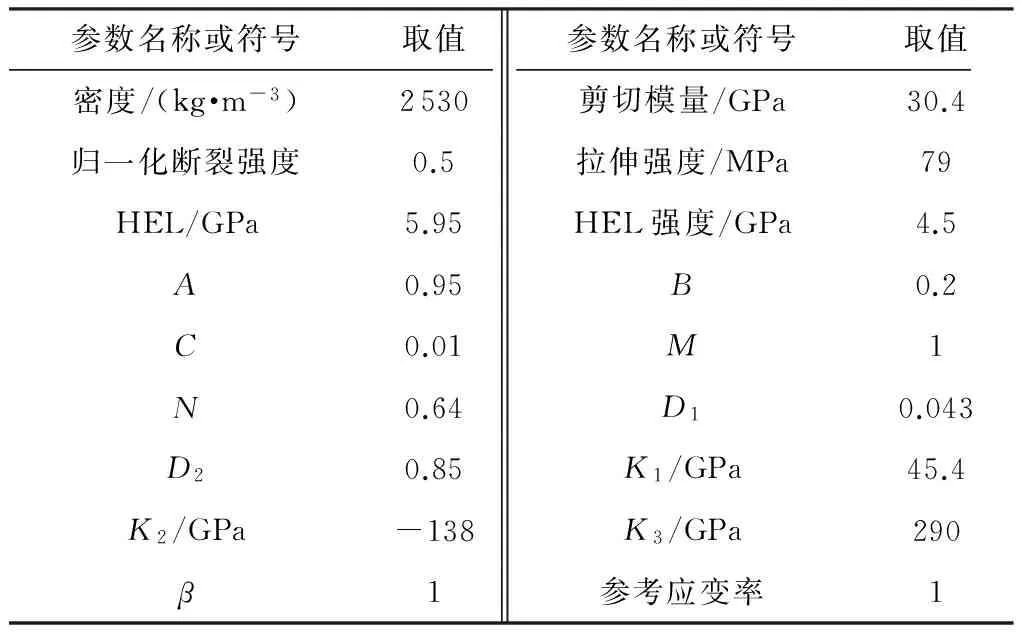
表1 浮法玻璃的JH2模型参数1)

1)A—归一化未破裂强度参数；B—归一化破裂后强度参数；C—应变率相关的强度参数；M—破裂后强度参数；N—未破裂强度参数；D1、D2—破裂的相关系数；K1、K2、K2—压力系数；HEL—弹性极限(Hugoniot Elastic Limit)；β—弹性能转化为静水压力下内能的比例.

表2 PVB和橡胶的材料参数

由于瑕疵不确定性等因素,浮法玻璃的拉伸强度T需依据具体试验材料来确定.如图3所示,T取80 MPa时板中心处挠度峰值比T取65MPa时的小19%,说明T值对挠度有较大影响.文中JH2中的T取为79 MPa.对比有限元模拟结果与Kranzer试验FX014的试验值发现,有限元模拟结果与试验结果吻合非常好,挠度峰值模拟值(15.5 mm)比试验值(15.0 mm)高3.3%左右,峰值对应时间(3.68 ms)与试验时间(3.70 ms)相差0.5%左右.有限元法得到的夹层玻璃中点法向速度与Kranzer试验法结果吻合较好,在2 ms后,玻璃发生了破坏,受该破坏行为的影响,由PVB节点法测得的法向速度存在波动,如图4所示.以上结果说明,文中采用的材料本构参数是合理、可靠的,可用于后文的相关研究.

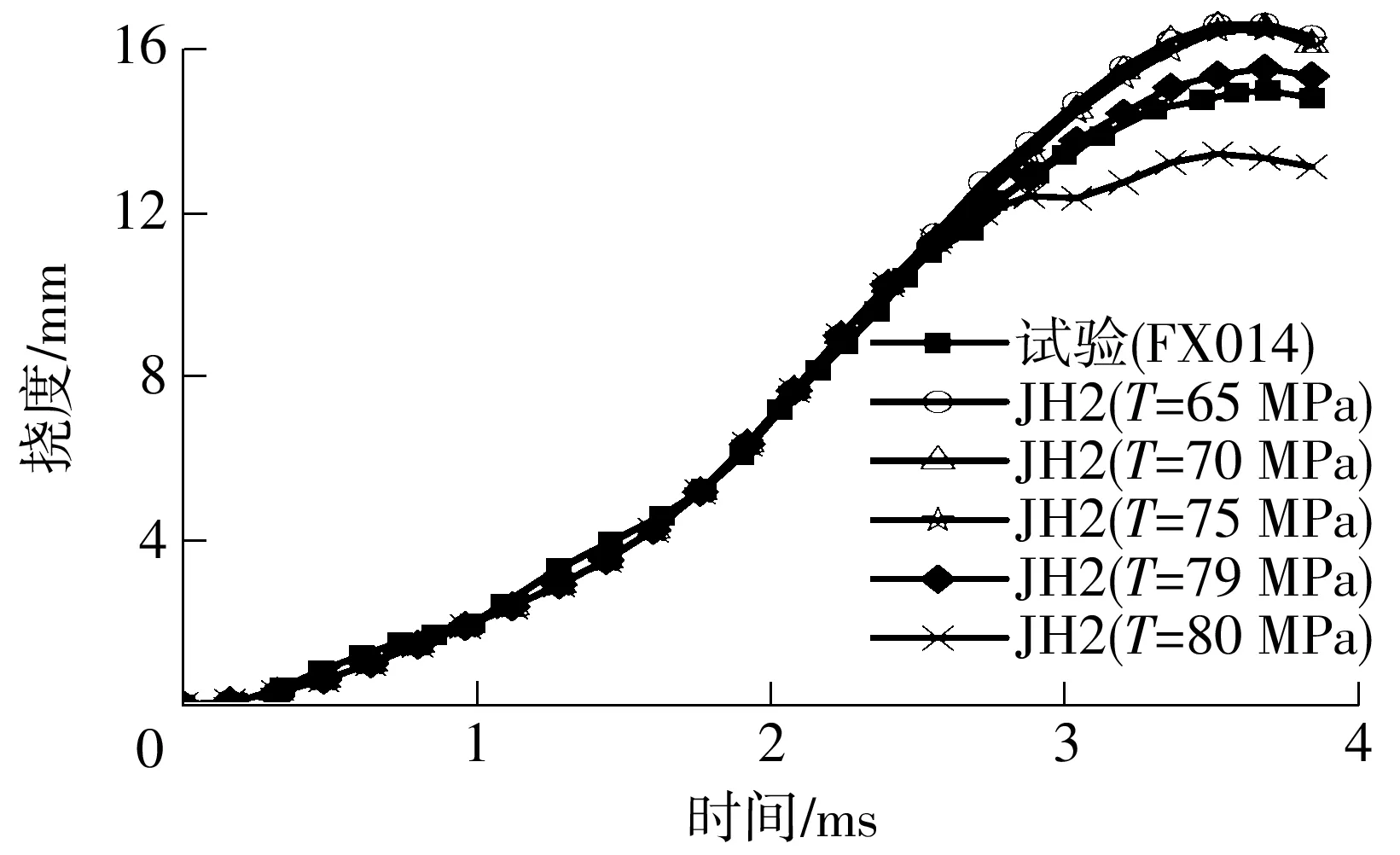
图3 T值对夹层玻璃中点挠度时程曲线的影响

Fig.3 Influence ofTvalue on midpoint deflection-time curves of laminated glass

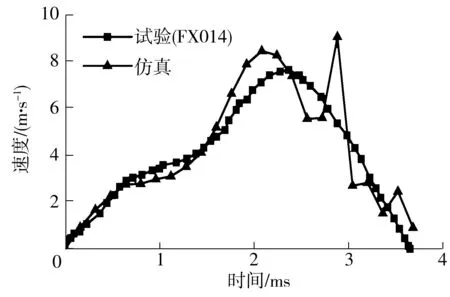
图4 Kranzer试验与有限元模拟得到的夹层玻璃中点法向速度时程曲线

Fig.4 Midpoint normal velocity-time curves of laminated glass respectively obtained by Kranzer’s test and finite element simulation

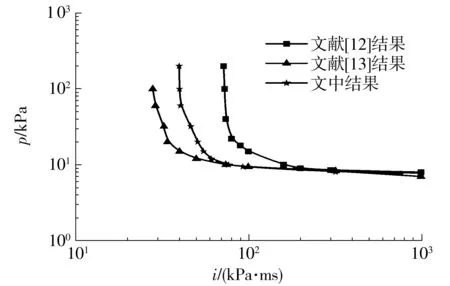
1.2p-i图验证

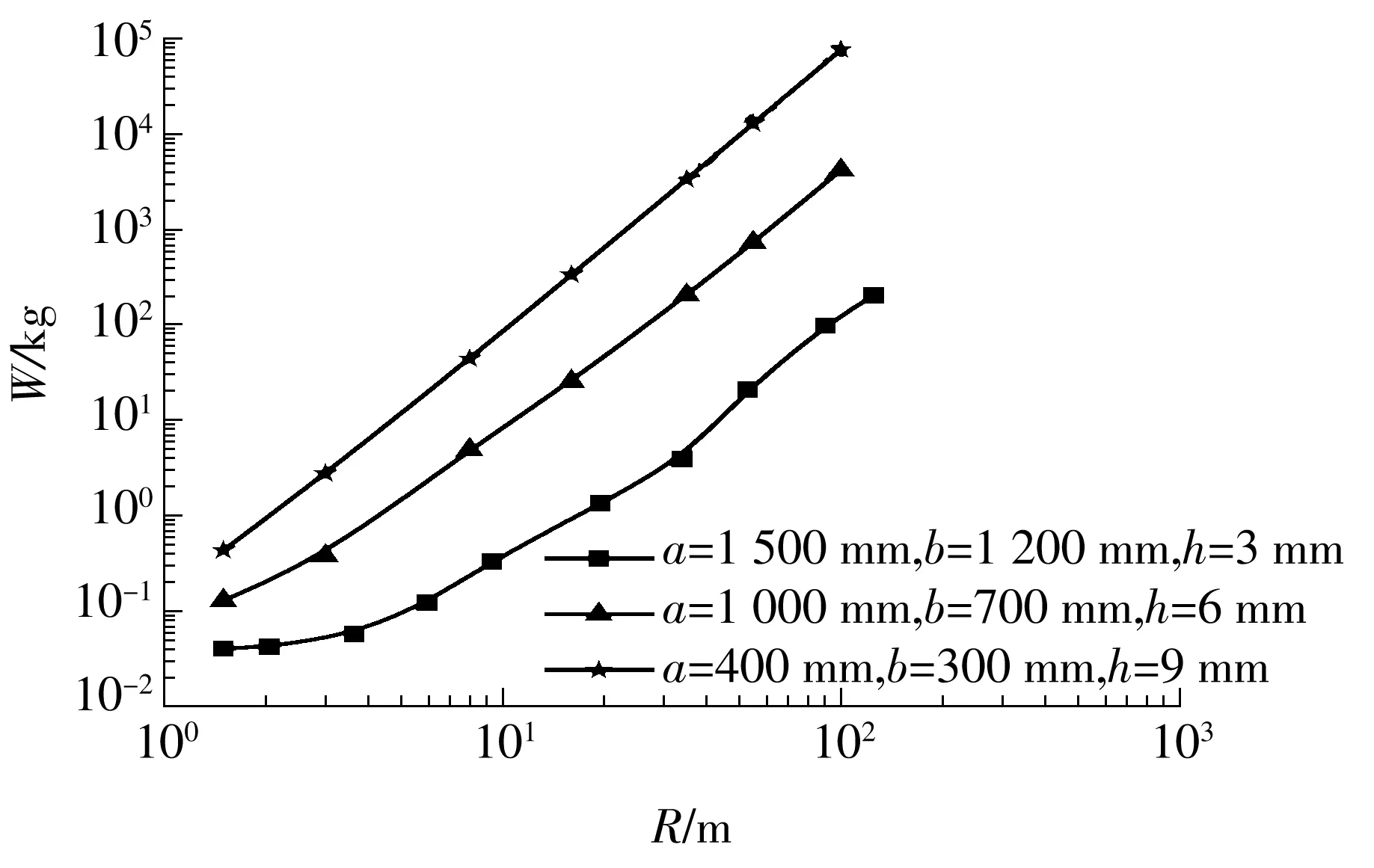
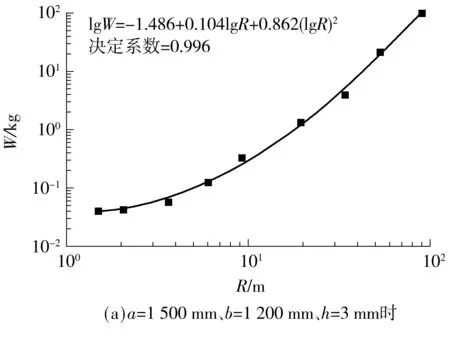
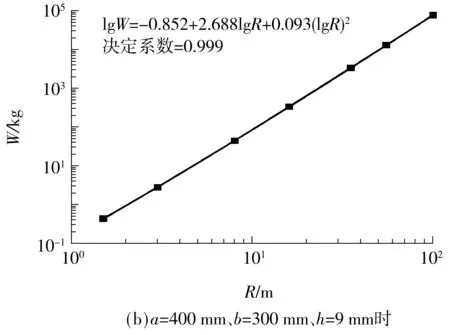
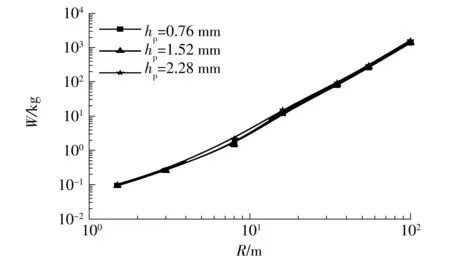
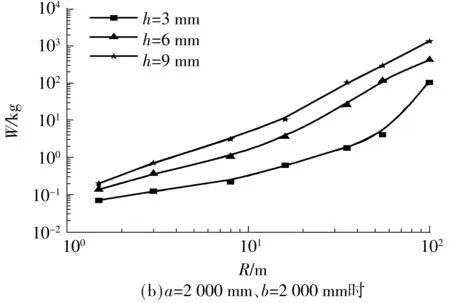
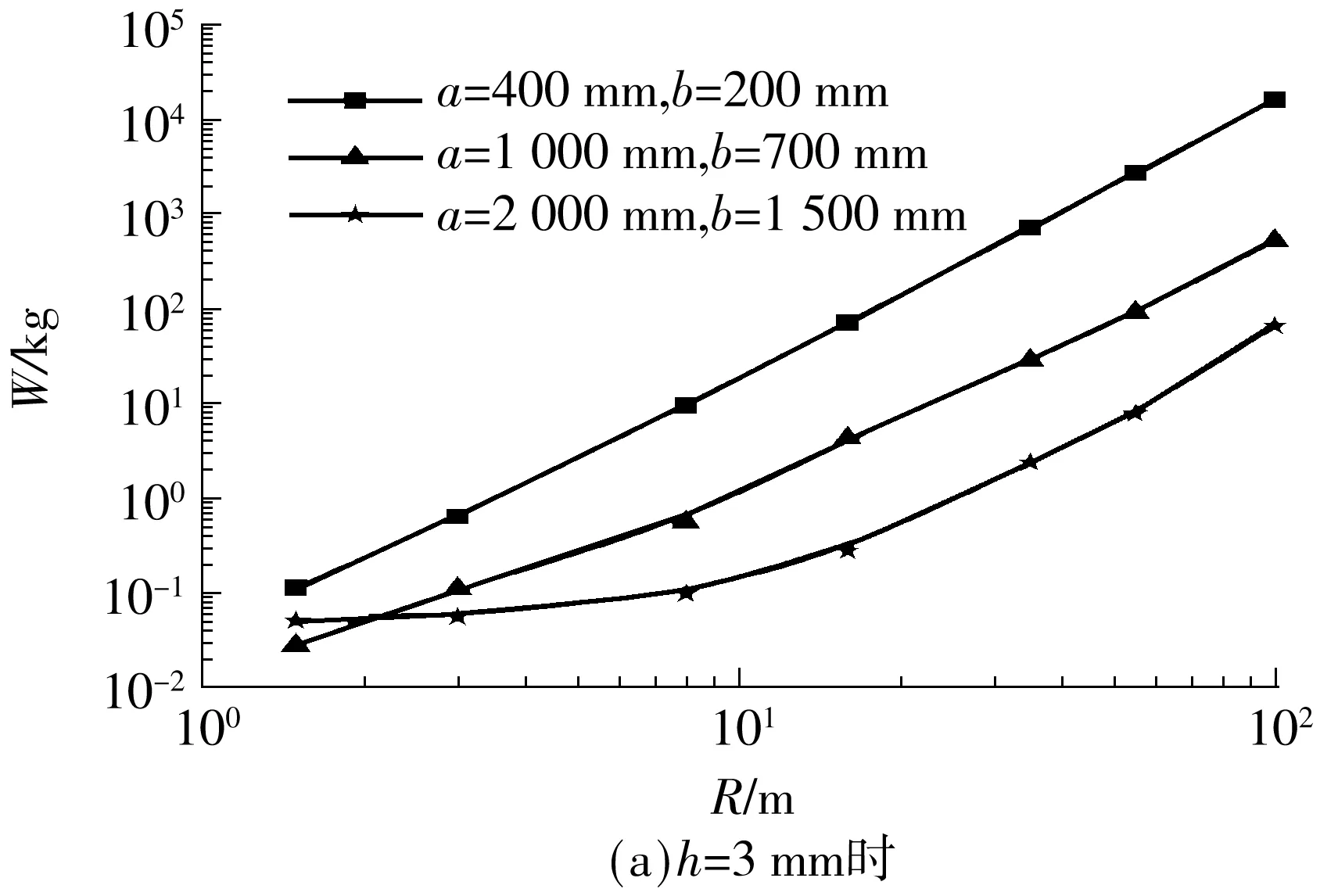
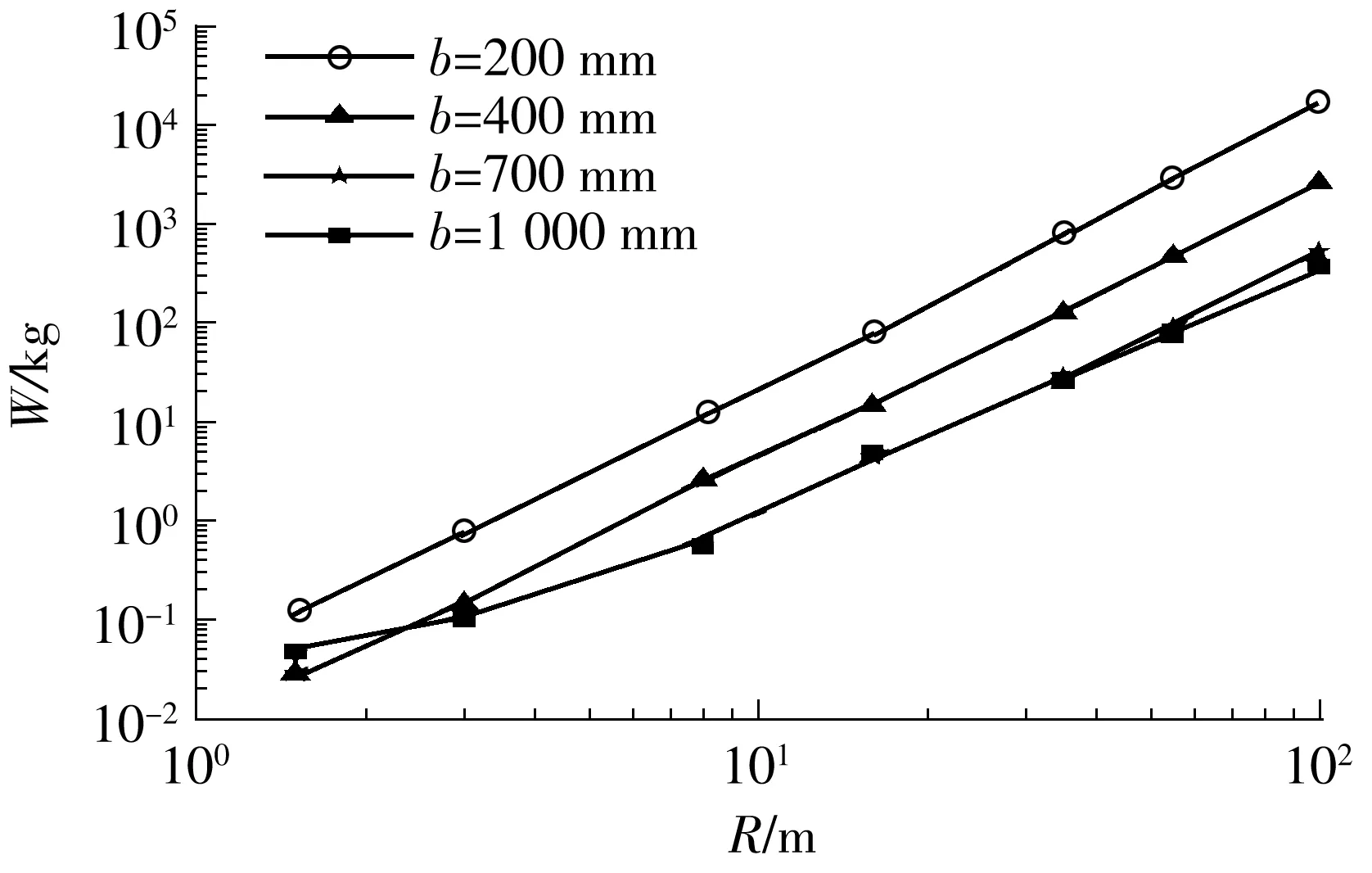
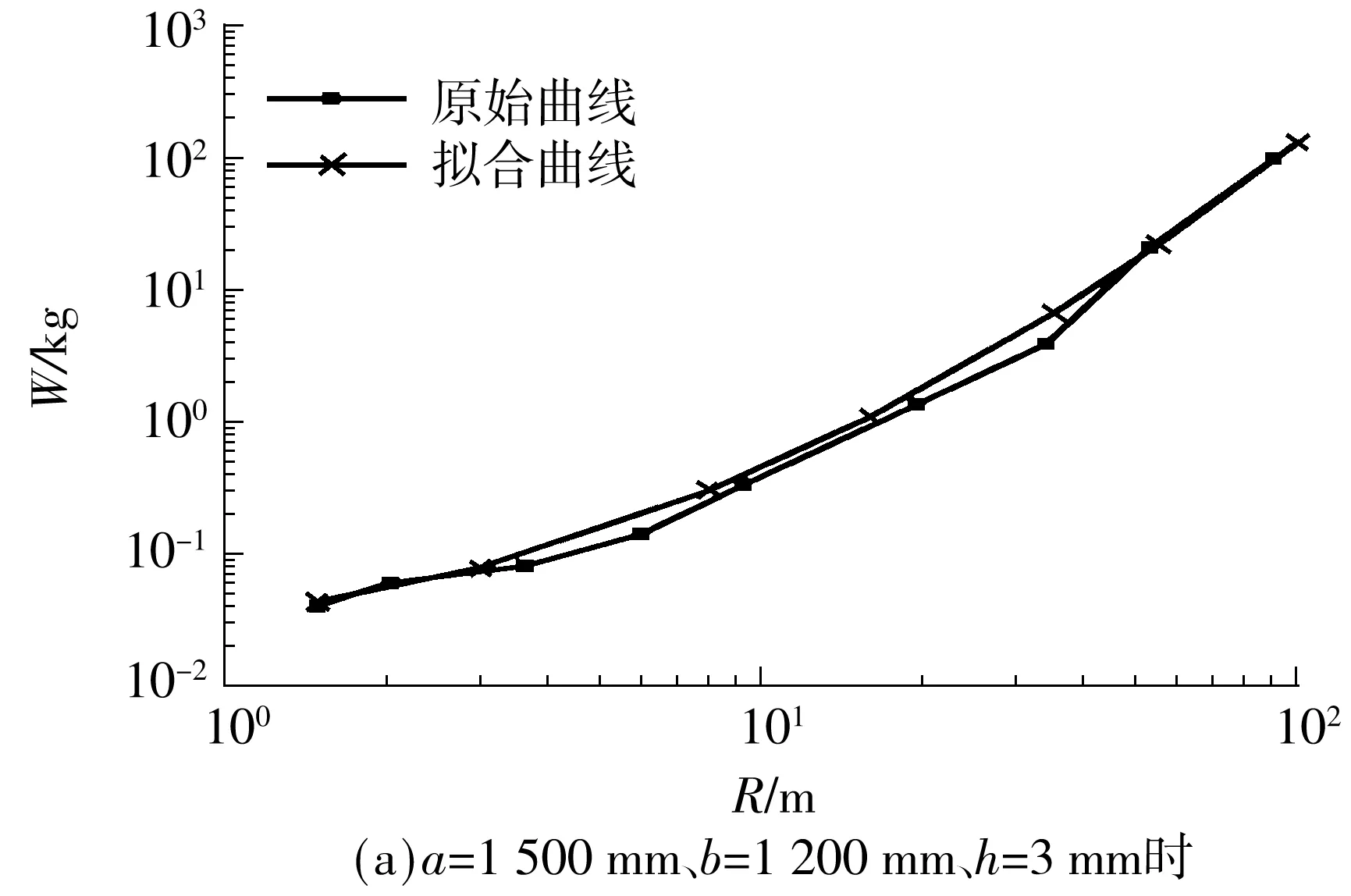
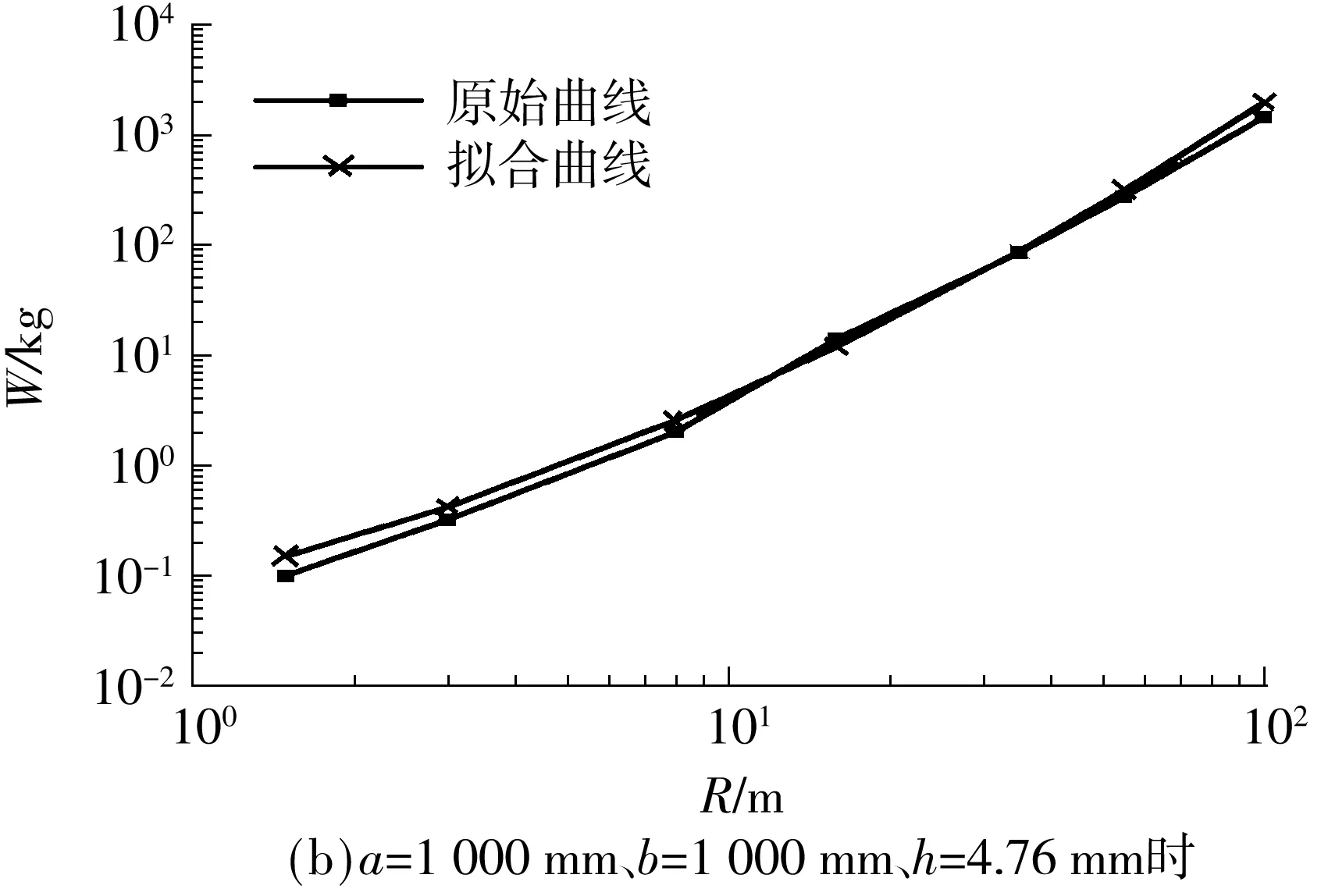
依据文献[11],典型的p-i曲线具有两个重要特征：水平渐近线和垂直渐近线.如图5所示,阶段Ⅰ代表正冲量控制的临界荷载,只要i

图5 典型的p-i曲线(对数坐标)

图6所示为未考虑负压段的p-i曲线与文献[12- 13]中结果的对比,其中,夹层玻璃尺寸如下：长度a=1 500 mm,宽度b=1 200 mm,内外层玻璃厚度h内=h外=3 mm,PVB厚度hp=1.52 mm.后文若无特别说明,PVB厚度固定为1.52 mm,玻璃等厚度(h),受边界固支约束.从图6可以看出,文中所得的p-i曲线在Ⅰ和Ⅱ段居于文献[12]与[13]所得的p-i曲线之间,而在Ⅲ段与文献结果吻合很好.三者的差异在于：文献[12]中采用把夹层玻璃简化成单自由度系统的方法,文献[13]中对玻璃采用线弹性本构(失效应力为80 MPa),而文中采用JH2本构(失效塑性应变为0.000 1)模拟浮法玻璃,玻璃本构以及失效定义的差异很可能造成p-i曲线的差异.p-i曲线对比结果也表明,文中有限元模拟采用的材料参数取值是合理的.

图6 p-i曲线对比

2 考虑负压段的抗爆设计方法

2.1 负压段对p-i图的影响

空气中的爆炸荷载p(t)可以描述成一个指数形式的函数表达式[14]：

(1)

式中,cr为正压放大系数,Δpf为爆炸超压峰值(MPa),t为时间(ms),t+为正压作用时间(ms),α为衰减系数.

Δpf可由下式得到[15]：

(2)

其中,Z由下式得到：

(3)

R为爆炸距离(m),W为炸药当量(kg).

t+可由式(4)求得[14]：

(4)

衰减系数α表示为

α=1.5Z-0.38, 0.1≤Z≤30

(5)

单位面积正冲量i+(kPa·ms)根据式(1)对时间t(t∈[0,t+])积分求得,即

(6)

正压放大系数cr为

(7)

其中p1=Δpf+p0,环境气压p0约为101.3kPa.

事实上,忽略负压段的影响有可能会低估爆炸荷载的作用.根据文献[14]和[16],负压段的影响程度与结构的固有频率有关.一般而言,结构的固有频率越低,越可能受负压段影响.文中对夹层玻璃进行了考虑负压段的p-i曲线研究,定性分析了固有频率与负压段对夹层玻璃p-i曲线的影响.如图7(a)所示,由于夹层玻璃固有频率较低(22Hz),在Ⅰ和Ⅱ段,负压段起的作用是不可忽略的,忽略负压段会高估夹层玻璃的抗爆炸临界荷载.在Ⅲ段,负压段对p-i曲线无明显影响.如图7(b)所示,当玻璃尺寸变小、厚度增加、固有频率增大(93Hz)时,负压段所起作用减小.如图7(c)所示,当夹层玻璃固有频率足够大(481Hz)时,负压段影响可忽略.图中的细微差异是由于考虑爆炸负压段影响时是按指数衰减形式(式(1))来计算爆炸荷载的,未考虑负压段影响时则是采用简化三角形脉冲荷载来计算爆炸荷载,即

(8)

虽然p-i曲线为夹层玻璃的抗爆设计提供了极大的便利,但考虑负压段可能会对夹层玻璃的动态响应产生影响,因此需要对p-i曲线做适当修正,垂直段Ⅰ可能失去冲量渐近线这一重要特性,呈非单值性,并且,垂直段Ⅰ对应中短爆炸距离,这在实际中更为常见.若只保留水平段Ⅲ的超压渐近线,针对中短爆炸距离的情形会偏于安全,偏于安全的程度与夹层玻璃结构固有频率和爆炸工况等有关；而统一按水平段Ⅲ的超压渐近线设计,又可能过分低估玻璃的抗爆性能,造成浪费.因此,有必要进一步探讨新的夹层玻璃抗爆设计方法.

(a)a=1 500 mm、b=1 200 mm、h=3 mm、固有频率=22 Hz时

(b)a=1 000 mm、b=700 mm、h=6 mm、固有频率=93 Hz时

(c)a=400 mm、b=300 mm、h=9 mm、固有频率=481 Hz时

Fig.7 Influence of considering negative phase of blast or not onp-icurves

2.2W-R法研究

文中考虑负压段,对3种尺寸的夹层玻璃p-i曲线(见图7)进行了进一步的研究,根据有关计算公式,某一数据点(p,i)必对应另一数据点(W,R),故可以把图7所示的的p-i图转换成如图8所示的W-R图.

从图9所示W-R拟合曲线可以发现：经多项式拟合后,W-R函数具备较为简单的形式,拟合二项式的决定系数均达0.99,拟合效果相当好.对于负压段影响不大的尺寸(a=400 mm,b=300 mm,h=9 mm),其W-R曲线近似一条直线,二次项系数很小；若负压段影响较大,则中短爆炸距离的W-R函数是曲线形式,二次项系数较大；在不受负压段影响的远距离区域,W-R函数依旧保持直线形式,如尺寸a=1500 mm、b=1200 mm、h=3 mm时.

图8 不同尺寸夹层玻璃的W-R曲线

图9 W-R拟合曲线

由上可见：W-R曲线具有规律性——当负压段影响不大时表现为直线,当负压段影响较大时表现为二次曲线；W-R图同样具有直观性——直接给出了某爆炸距离R下某夹层玻璃尺寸的临界炸药当量W；W-R函数表达式简单,便于抗爆设计应用；采用W-R法进行抗爆设计具有可行性.

2.3 尺寸参数对W-R图的影响

2.3.1 PVB厚度的影响

随着PVB厚度的增加,夹层玻璃临界荷载W-R曲线略向上偏移,但变化不大,如图10所示.PVB厚度为2.28 mm时的W值比厚度为0.76 mm时的仅增大20%左右(R=8 m),相比玻璃厚度的增加,W值增大效果不明显,故文中忽略其影响.

图10 PVB厚度对W-R曲线的影响

2.3.2 玻璃厚度的影响

不同尺寸夹层玻璃的玻璃厚度对W-R曲线的影响见图11.

图11 玻璃厚度对W-R曲线的影响

由图11可见W-R曲线最明显的特性：不论夹层玻璃尺寸大小,玻璃厚度的增加均使W-R曲线往上移动,说明玻璃厚度的增加可有效提高夹层玻璃的抗冲击承载力；随着夹层玻璃尺寸的增大,固有频率降低,近距离负压段影响变大,W-R曲线由线性(见图11(a))变为非线性(见图11(b)).

2.3.3 夹层玻璃面积的影响

如图12所示,随着夹层玻璃面积的增加,W-R曲线大体向下偏移,夹层玻璃抗冲击承载力下降.R=8 m时,2 000 mm×1 500 mm夹层玻璃(h=3 mm)的临界W值约是400 mm×200 mm玻璃的1%；2 000 mm×2 000 mm夹层玻璃(h=6 mm)的临界W值约是400 mm×400 mm玻璃的4.9%,这说明面积的增加会导致夹层玻璃抗冲击承载力的急速下降.

2.3.4 玻璃长宽比的影响

如图13所示,当夹层玻璃宽度由200 mm增加到400和700 mm时,W-R曲线下移,R=8 m时,宽度为400和700 mm的夹层玻璃对应的W值分别降低到宽度为200 mm的玻璃的22.6%和5.0%,而宽度为700和1 000 mm的夹层玻璃的W-R曲线相差较小.这说明,狭长的矩形夹层玻璃有利于抗冲击承载力的提高,长宽比例接近1的夹层玻璃构造反而于抗冲击性无益.

图13 长宽比对W-R曲线的影响

2.4W-R经验公式

根据前文结果,假设W-R函数的一般形式如下：

lgW=A×(lgR)2+B×lgR+C

(9)

式中,系数A、B和C与夹层玻璃尺寸有关,一般夹层玻璃长宽比越小,玻璃厚度越大,结构固有频率越高,负压段影响越不显著,W-R曲线就越接近直线,相应地,系数A越小,B和C越大.可假设A、B和C与夹层玻璃尺寸a、b和h的关系满足以下公式：

(10)

(11)

(12)

设定玻璃厚度分别为3、6和9mm,长度分别为400、1 000和2 000mm,在4种宽度共计36(3×3×4=36)种玻璃尺寸下探讨矩形夹层玻璃不等边的情形.爆炸距离R分别为1.5、3.0、8.0、16.0、35.0、55.0和100.0m,于是共有252(36×7=252)个(R,W)数据点.采用1stOpt中的麦夸特法和通用全局优化法拟合系数A、B和C,得

0.285)+2.222

(13)

5.075)+6.803

(14)

1.341)-0.887

(15)

系数A随玻璃厚度h的增加而减小,系数B和C则随h增加而增大；系数A随玻璃面积增大而增大,系数B和C则随玻璃面积增大而减小,这与参数影响的定性分析结果是一致的,且拟合的效果很好,决定系数为0.996,相关系数为0.998.取两种尺寸的夹层玻璃(不用于拟合W-R函数)的W-R曲线与拟合函数预估曲线进行对比,所得结果如图14所示.除了少数(R,W)数据点的预估误差可能较大(25%～40%)外,多数点的预测效果较好,这表明将拟合的W-R函数用于预测夹层玻璃以玻璃临界破坏为基准的抗爆炸冲击临界荷载是可行的.误差产生的原因主要在于：虽然研究的尺寸参数有3个,且玻璃厚度和长度分别取3个值,长宽比取4个值,爆炸距离取7个值,计算量很大,但相对于每个参数来说,数据量仍然不够；另外,假设的系数函数不够精确,不能完全反映客观规律.因此,拟合的W-R函数用于预测研究参数取值范围内的W-R曲线是具备一定精度的,但很可能不适用于外推,需要用更多数据来分析才可行.

图14 原始W-R曲线与拟合预测W-R曲线的比较

Fig.14ComparisonoforiginalandfittedpredictionalW-Rcurves

3 结语

文中对抗爆设计p-i图进行了爆炸负压段影响的研究,发现爆炸负压段对夹层玻璃的动态响应一般是不可忽略的.鉴于现有p-i图法的不足,文中探讨了一种新的抗爆设计方法——W-R图法,得到了以玻璃临界破坏为基准的评估夹层玻璃抗爆特性的W-R经验公式.尽管精度还不够理想,但该W-R函数考虑了夹层玻璃的尺寸(长度、宽度、玻璃厚度),可以给出某尺寸玻璃的W-R曲线并将其直接用于抗爆设计,因此对W-R抗爆设计方法的完善有较大工程意义与学术价值.后续研究中,将探讨进一步提高W-R经验公式精度的途径,并开展相应的爆炸试验研究,为W-R图法提供依据.

[1] Bruck T.The economic consequences of the new global terrorism [J].Economic Bulletin,2002,39(10):327- 332.

[2] Norville S,Conrath E J.Considerations for blast-resistant glazing design [J].ASCE:Journal of Architectural Engineering,2001,7(3):80- 86.

[3] 高轩能,江媛,王书鹏.建筑玻璃的爆炸动力响应及防爆距离 [J].计算力学学报,2011,28(4):560- 565. Gao Xuan-neng,Jiang Yuan,Wang Shu-peng.Dynamic response of architectural glass to explosion and safe extent research[J].Chinese Journal of Computational Mecha-nics,2011,28(4):560- 565.

[4] Wei Ya,Chen Suwen,Au T K Francis.Failure analysis of four-point-supported glass panels subjected to blast loading [EB/OL].(2013- 04- 29) [2015- 03- 20].http:∥www.tandfonline.com/doi/full/10.1080/1023697X.2013.785089#abstract.

[5] Zhang X H,Hao H,Ma G W.Parametric study of lamina-ted glass window response to blast loads [J].Engineering Structures,2013,56(6):1707- 1717.

[6] Krauthammer T,Altenberg A.Negative phase effects on glass panels [J].International Journal of Impact Engineering,2000,24(1):1- 18.

[7] Jun W,Dharani Lokeswarappa R.Response of laminated architectural glazing subjected to blast loading [J].International Journal of Impact Engineering,2006,32(12):2032- 2047.

[8] Kranzer C,Gürke G,Mayrhofer C.Testing of bomb resis-tant glazing systems:experimental investigation of the time dependent deflection of blast loaded 7.5 mm maminated glass [EB/OL].(2005- 08- 31) [2015- 03- 20].http:∥www.glassfiles.com/articles/testing-bomb-resistant-glazing-systems-experimental-investigation-time-dependent-deflection.

[9] Larcher Martin,Solomos George,Casadei Folco,et al.Experimental and numerical investigations of laminated glass subjected to blast loading [J].International Journal of Impact Engineering,2012,39(1):42- 50.

[10] Hidallana-Gamage H D,Thambiratnam D P,Perera N J.Failure analysis of laminated glass panels subjected to blast loads [J].Engineering Failure Analysis,2014,36(1):14- 29.

[11] Li Q M,Meng H.Pressure-impulse diagram for blast loads based on dimensional analysis and single-degree-of-freedom model [J].Journal of Engineering Mecha-nics,2002,128(1):87- 92.

[12] Cormie D,Mays G,Smith P.Blast effects on buildings [M].2nd ed.London:Thomas Telford,2009.

[13] Hooper P A,Sukhram R A M,Blackman B R K,et al.On the blast resistance of laminated glass [J].International Journal of Solids and Structures,2012,49(6):899- 918.

[14] Teich M,Gebbeken N.The influence of the under pressure phase on the dynamic response of structures subjected to blast loads [J].International Journal of Protective Structures,2010,2(1):219- 234.

[15] Sadovskiy M A.Mechanical effects of air shockwaves from explosions according to experiments [M]∥Sadovskiy M A.Selected works:Geophysics and Physics of Explosion.Moscow:Nauka Press,2004.

[16] Yang Mijia,Ahmari Saeed.Investigation of effect of ne-gative phase of blast loading on cable net curtain walls through the linearized stiffness matrix method [J].International Journal of Impact Engineering,2013,61(4):36- 47.

W-RMethod for Blast Resistance Design of Laminated Glass

ZhangHongDengHan-guoYaoXiao-huLongQian

(School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640,Guangdong,China)

The blast resistance design of laminated glass helps to reduce the personal injury caused by explosive blast. The traditional blast resistance design withp-idiagram, wherepis overpressure andiis positive impulse per unit area, does not take into consideration the effect of negative phase of blast. However, the negative phase can significantly affect the dynamic response of laminated glass. In order to solve this problem, the effect of the negative phase of blast on thep-idiagram is simulated by means of the finite element method. Aiming at the deficiency of thep-idiagram design method for blast resistance, a design method namedW-Rmethod, whereWrefers to explosive equivalent andRrefers to explosion distance, is developed for blast resistance. In comparison with thep-idiagram design method, theW-Rdesign method is more feasible for the blast resistance design because theW-Rdiagram has a simpler form and is more regular and more intuitional. Furthermore, the effects of the geometric parameters of laminated glass on its impact resistance are qualitatively analyzed, and by taking the critical damage of laminated glass as the benchmark, an empiricalW-Rformula is fitted to evaluate the blast resistance of laminated glass, which can provide guidance for the blast resistance design of laminated glass.

laminated glass; blast resistance;critical damage;explosive equivalent;explosion distance; finite element method

2015- 04- 10

国家自然科学基金资助项目(11372113) Foundation item: Supported by the National Natural Science Foundation of China(11372113)

张红(1967-),女,博士,副教授.主要从事复合材料及其结构力学和冲击动力学研究.E-mail: emhzhang@scut.edu.cn

1000- 565X(2015)11- 0119- 08

TU 382

10.3969/j.issn.1000-565X.2015.11.017