新型功率分流混合动力汽车的动力性优化*

王晨 郭明林 刘国志

(1.同济大学 新能源汽车工程中心， 上海 201804; 2.上海交通大学 机械与动力工程学院， 上海 200240;3.科力远混合动力技术有限公司 系统控制科， 上海 201501)

新型功率分流混合动力汽车的动力性优化*

王晨1郭明林2刘国志3

(1.同济大学 新能源汽车工程中心， 上海 201804; 2.上海交通大学 机械与动力工程学院， 上海 200240;3.科力远混合动力技术有限公司 系统控制科， 上海 201501)

动力性是整车的重要性能指标之一.为研究混合动力汽车的动力性优化问题，按照车速序列将全油门加速过程转化为多级决策过程，提出了动力性优化问题的动态规划求解方案;建立了新型功率分流混合动力汽车模型，基于Matlab仿真平台得到了全局最优控制策略;同时，建立了双电机转矩图，定义电机速比及动力电池功率带，分析、归纳了全油门加速控制策略.整车动力性优化试验结果显示，优化后车辆的百公里加速时间减少了15.7%，基于动态规划算法的控制策略可显著提升整车动力性.

混合动力总成;加速控制;混合动力汽车;动态规划;优化

经济性与动力性是汽车性能的两大指标.混合动力汽车可降低油耗，并具有很好的动力性[1- 3].由于混合动力技术节油效果显著，目前针对混合动力汽车的研究主要集中在燃油经济性，关于动力性的研究则主要是对整车开发前期的参数匹配进行仿真[4- 7].

动态规划算法是优化算法的一种，目前已广泛应用于混合动力汽车控制策略优化来提高燃油经济性.按照时间序列，将车辆驾驶过程划分为多级决策过程，以整车能量消耗最小为控制目标，建立动态规划问题，可求得既定工况下的最优控制策略[8- 9].

文中将动态规划算法应用于整车控制策略动力性优化,目的是将动力性优化工作从参数匹配阶段扩展至性能优化调试阶段，并为整车性能优化调试阶段提供理论指导和工程应用方法.考虑到动力性和经济性往往相互制约，不能实现同时最优，为深入研究系统动力性，研究中仅以动力性为优化指标而忽略对经济性的影响.

1 动态规划动力性仿真方案的设计

1.1 动力性定义

整车的动力性能包括加速能力、最高车速和最大爬坡度，其中最高车速与最大爬坡度主要通过参数匹配设计实现优化.文中选取加速度能力表征整车动力性，通过优化控制策略、减少百公里加速时间来提高动力性.百公里加速时间是指混合动力汽车处于混合动力模式时，整车由静止开始全油门加速至100 km/h所用的时间.

1.2 动力性问题动态规划求解方案的设计

动态规划是将一个多级决策问题简化为一系列单级决策过程的运筹学方法，经过计算可以得到全局最优解.全油门加速过程中，车速从零增加至100 km/h，可根据车速序列将其划分为一个多级决策过程，即每隔一定车速差为一级,通过调整每一级的整车状态，使得整车动力性达到最优.

动态规划的一般表述如下：

N级过程的状态方程组为

(1)

式中：k=0,1,…,N-1;状态变量x(k)与控制变量u(k)的约束条件分别为

x(k)∈X⊂Rn

(2)

u(k)∈Ω⊂Rm

(3)

求最优控制序列u*(k)，使得代价函数最小，代价函数为

(4)

功率分流混合动力汽车可实现发动机转速与轮边车速的解耦.通过选取发动机转速为状态变量、发动机转动加速度为控制变量，确定每一级状态下的车速与发动机转速，则仅需调整发动机与电机转矩状态即可确定整车驱动转矩，实现系统状态转移.状态方程组为

(5)

式中：nE为发动机转速，r/min;aE为发动机加速度，rad/s2;Δt(k)为第k级转移至k+1级所用的时间，

(6)

(7)

v(0)=0km/h,v(N)=100km/h，v为车速，km/h;mv为整车质量，kg;Fpro为整车驱动力，N和Fresi为整车阻力.

动力性代价函数以加速时间来建立[6]，时间越短，动力性越好.动力性代价函数表示如下：

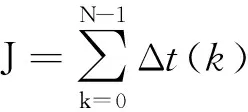
(8)

2 新型功率分流混合动力系统方案

2.1 混合动力系统结构设计

图1所示为新型功率分流混合动力系统[10- 12]的结构.混合动力汽车的主要机构包括发动机、小电机E1、大电机E2、镍氢动力电池、双行星排混合动力变速箱、主减速器和差速器.其中，发动机与镍氢动力电池作为驱动能量源，为整车提供驱动力.发动机与变速箱的行星架PC相连，小电机E1与前行星排太阳轮S1相连，大电机E2与后行星排太阳轮S2相连，变速箱的齿圈R与主减速器相连.制动器B1与行星架相连，用于锁止行星架，制动器B2与小电机E1相连，用于锁止小电机E1.

图1 新型功率分流混合动力系统的结构

Fig.1 Configuration of novel power-split hybrid power system

2.2 整车参数

表1所列为新型功率分流混合动力汽车的整车参数.

表1 新型功率分流混合动力汽车的整车参数

2.3 整车状态约束

2.3.1 双行星排混合动力变速箱模型

由行星齿轮运动学和动力学可得到混合动力变速箱各部件的转矩关系[13- 14]：

TE-JEαE=TPC

(9)

T1-J1α1=TS1

(10)

T2-J2α2=TS2

(11)

-TO-JRαR=TR

(12)

TPC+TS1+TS2+TR=0

(13)

(1-i1)TS1+(1-i2)TS2+TE=0

(14)

式中：TE为发动机转矩;TPC为行星架转矩;T1为电机E1转矩;TS1为太阳轮S1的转矩;T2为电机E2转矩;TS2为太阳轮S2的转矩;TO为输出轴输出转矩;TR为齿圈转矩;JE为发动机转动惯量;J1为电机E1转动惯量;J2为电机E2转动惯量;JR为齿圈上的整车当量转动惯量;α1为电机E1加速度;α2为电机E2加速度;αR为齿圈加速度;i1为前行星排传动比，即太阳轮S1到行星架PC的等效杠杆距离[15];i2为后行星排传动比，即太阳轮S2到行星架PC的等效杠杆距离.

转速关系由前后行星排传动比决定：

n1=nOi1+nE(1-i1)

(15)

n2=nOi2+nE(1-i2)

(16)

式中：nO为变速箱输出轴转速;n1为太阳轮S1转速，即电机E1转速;n2为太阳轮S2转速，即电机E2转速.图2为混合动力变速箱四轴等效杠杆图[13- 14]，各纵轴位置表征当前轴转速，横轴Lref以上转速为正，Lref以下转速为负.各轴上箭头表示作用于各部件轴上的转矩，箭头向上则转矩为正，向下则转矩为负.

图2 混合动力变速箱四轴转速等效杠杆

2.3.2 车辆动力学模型

由车辆动力学可得

(17)

(18)

Fresi=-(Ff+Fw+Fi+Fj)

(19)

式中：r为车轮半径;i为主减速器齿轮传动比;Ff为滚动阻力;Fw为空气阻力;Fi为坡度阻力，文中考虑平直路面，不考虑坡度;Fj为加速阻力，已在代价函数中体现，故取为0.

2.3.3 发动机模型

图3所示为发动机万有特性，其中，发动机转矩外特性取决于发动机转速.

图3 发动机万有特性图

2.3.4 电机模型

图4和5分别为电机E1和E2的特性曲线，其中，电机的转矩外特性取决于电机转速.电机额外功率损耗取决于电机当前转速与转矩.

图4 电机E1的特性曲线

图5 电机E2的特性曲线

2.3.5 动力电池模型

百公里加速时间短，故可忽略温度的影响，将动力电池模型简化为充放电功率不大于20 kW的电源，则有

(20)

式中：Pmin、Pmax分别为当前动力电池功率的上、下限，正为放电，负为充电;η1为电机E1工作效率;η2为电机E2工作效率;φ为电机工作模式，发电模式为1，电动模式为-1.

3 动态规划仿真结果与分析

3.1 动态规划仿真结果

动态规划仿真结果如图6-8所示.

图6 发动机加速度控制曲线

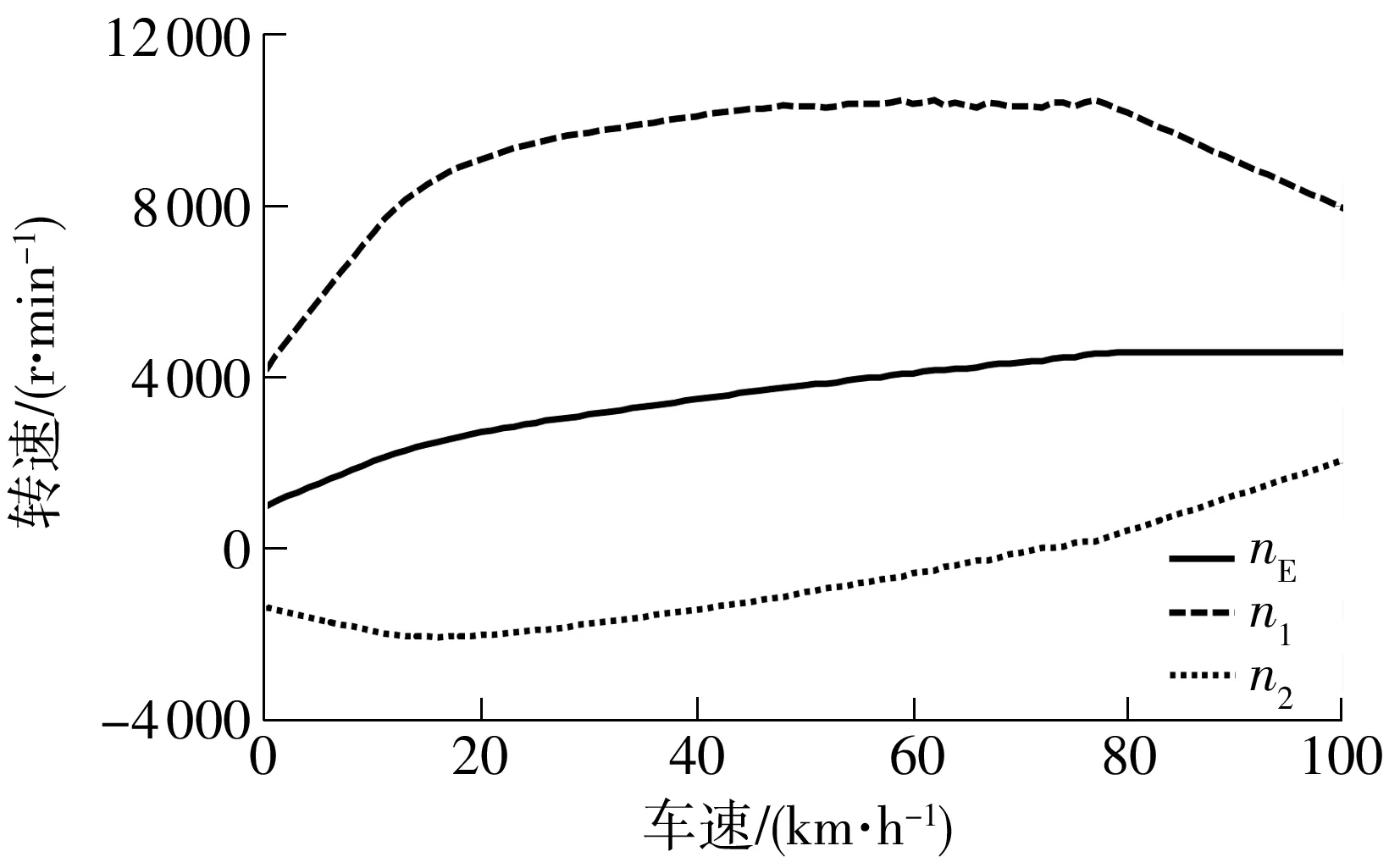
图7 三轴转速曲线

图8 四轴转矩曲线

根据动态规划仿真结果，可得控制策略如下：在[0,20]km/h车速区间，快速提高发动机转速;在(20,80]km/h车速区间，缓慢提高发动机转速，并维持电机E1转速，防止E1超限;在(80,100]km/h车速区间，维持发动机的高转速.

3.2 双电机转矩图

3.2.1 线性规划问题转化

虽然动态规划算法可针对非线性系统优化问题求得全局最优解，但是仿真结果难以揭示控制规律.为便于分析系统控制规律，忽略电机额外功率损耗和四轴转动惯量.每一级下变速箱四轴转速已知，则在系统特性约束下，实现整车驱动力最大即实现变速箱输出转矩最大.经转化，动力性优化问题如下：

max:TO=TE+T1+T2

(21)

s.t.

(1-i1)T1+(1-i2)T2+TE=0

(22)

T1(n1)min≤T1≤T1(n1)max

(23)

T2(n2)min≤T2≤T2(n2)max

(24)

(25)

式中，T1(n1)min和T1(n1)max、T2(n2)min和T2(n2)max分别为电机E1、E2在当前转速下的最小和最大可执行转矩.

3.2.2 双电机转矩图原理

以电机E1转矩为横坐标、电机E2转矩为纵坐标，并以两电机转矩工作点表征系统状态，建立图9所示的双电机转矩图(T-T图).

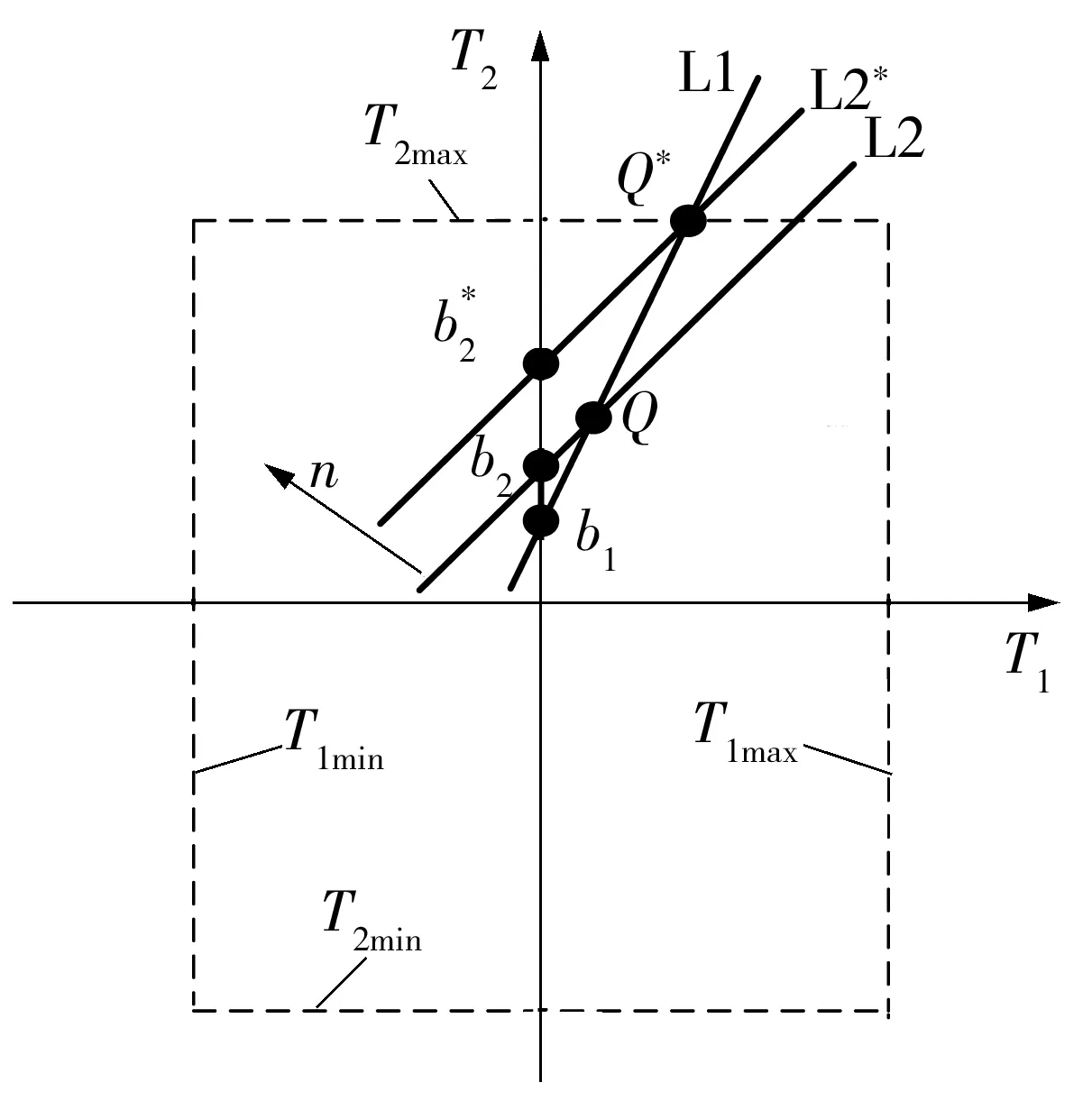
图9 双电机转矩图原理

虚线对应于当前转速下两电机的转矩限值，虚线矩形框内为电机可行域，等价于式(23)和(24)

将式(22)移项，前后行星排传动比取常数，得直线L1方程如下：

(26)

以式(22)为约束条件，则电机转矩必满足式(26)，T-T图上电机工况点需在直线L1上.直线L1与纵轴交于截距点b1，

b1=0.74TE

(27)

b1越大表明发动机转矩越大.将式(21)和(22)合并消除TE，得

TO=i1T1+i2T2

(28)

式(28)与式(21)等价，为便于分析，以式(28)代替式(21)作为动力性优化问题的代价函数.将式(8)移项，前后行星排传动比取常数，得直线L2方程如下：

(29)

直线L2与纵轴交于截距点b2，

b2=0.42TO

(30)

b2越大表明系统输出转矩越大.直线L1与L2相交于电机工作点Q，对应电机工况点(T1Q,T2Q).

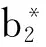
3.2.3 电机速比

双电机转矩图对应的是两电机之间的转矩关系.为研究四轴转速状态对控制策略的影响，引入电机速比ε，

(31)

由电机的转速与转矩状态可以确定电回路的状态.对式(25)，忽略电机的工作效率，得电回路功率如下：

(32)

图10为引入电机速比的T-T图.对于电机当前工作点Q，当前的电机速比为εQ，则必然存在直线L3过点Q，直线L3方程如下：

T2=εQT1+b3

(33)

图10 引入电机速比的T-T图

在电机E2转速非零的前提下，式(33)可等价为式(32).直线L3的截距b3如下：

(34)

式中，PLQ为电机工作点Q的电回路功率，n2Q为Q点对应的电机E2转速.由定义可知，b3为动力电池当前功率在电机E2转速下的折合转矩.当L3截距为零时，两电机之间功率均衡，表明动力电池当前功率为零，即为直线L4方程：

T2=εQT1

(35)

L4为L3的特例.由于直线L4方程只与电机速比相关，可用于表征四轴转速状态.转速杠杆图可简明地表征行星排机构的转速状态，引入电机速比后的T-T图可用于表示与转速杠杆图对应的系统转速状态.表2为T-T图的不同转速比区域划分，其中的黑色粗直线为特定的四轴转速下对应的直线L4，灰色区域为旋转轴转速变化范围内对应的系统状态下直线L4的变化区域.由于四轴转速范围的限制(即发动机转速不小于1 000 r/min，电机E1的转速上限为10 500 r/min，电机E2的转速上限为8 500 r/min)，可以得到电机速比的变化范围为[3.08，+∞)和(-∞，1.07]，所以[1.07，3.08]为系统电机速比的不可行域.

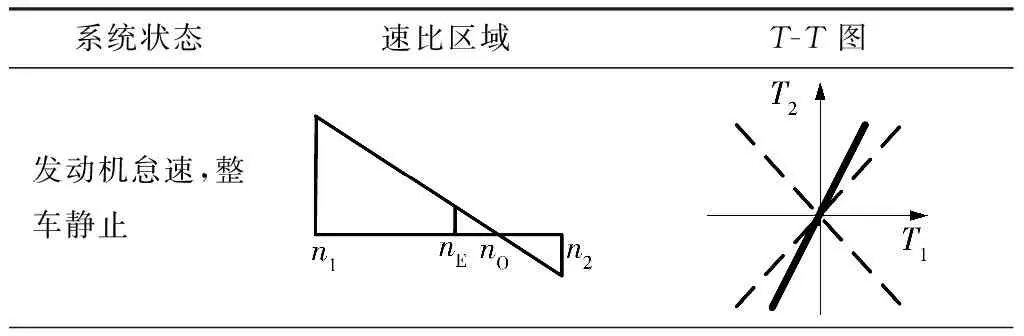
表2 T-T图的不同速比区域划分

续表2

系统状态速比区域T-T图电机E2负转速电机E2转速为零四轴正转速,电机E1转速大于电机E2四轴转速相等四轴正转速,电机E1转速小于电机E2电机E1转速为零电机E1负转速发动机怠速,电机E1负转速四轴转速约束造成的系统不可行域

3.2.4 功率带

式(25)给出了动力电池的功率限值.当电机速比不变时，电池当前功率对应直线L3.当动力电池当前功率为充放电功率极限时，可得电机速比εQ下的动力电池放电功率线L5和动力电池充电功率线L6.直线L5方程如下：

T2=εQT1+T2Pmax

(36)

直线L6方程如下：

T2=εQT1+T2Pmin

(37)

两直线与坐标轴的截距分别为

(38)

(39)

(40)

(41)

式中：T2Pmax和T2Pmin均为直线L3截距b3的特例，其中T2Pmax为动力电池最大放电功率Pmax仅供电机E2工作时所对应的电机E2转矩，T2Pmin为仅由电机E2产生动力电池最大充电功率Pmin时所对应的电机E2转矩;T1Pmax为直线L5在横坐标轴的截距，即动力电池最大放电功率Pmax仅供电机E1工作时所对应的电机E1转矩;T1Pmin为直线L6在横坐标轴的截距，即仅由电机E1产生动力电池最大充电功率Pmin时所对应的电机E1转矩.

在动力电池最大充放电功率限制下，直线L5与L6之间为直线L3的可行域，称为动力电池功率带.功率带的斜率由电机速比决定.在确定的电机速比下，功率带的宽度由动力电池可充放电功率范围[Pmin,Pmax]决定，充放电功率范围越大，功率带越宽.

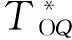
图11 功率带影响的T-T图原理

3.3 动态规划仿真结果分析

根据动态规划算法所得全油门加速过程控制策略的四轴转速，可得电机速比变化过程.图12所示为电机速比变化曲线.全油门加速过程中，电机速比ε先从3.08增大至188.10，在电机E2由负转速变化到正转速后，ε由188.10突变为-2 110.00，随后逐渐增大至-3.84.因此，全油门加速过程中，电机速比依次经历表2中前4个T-T图所示工况.

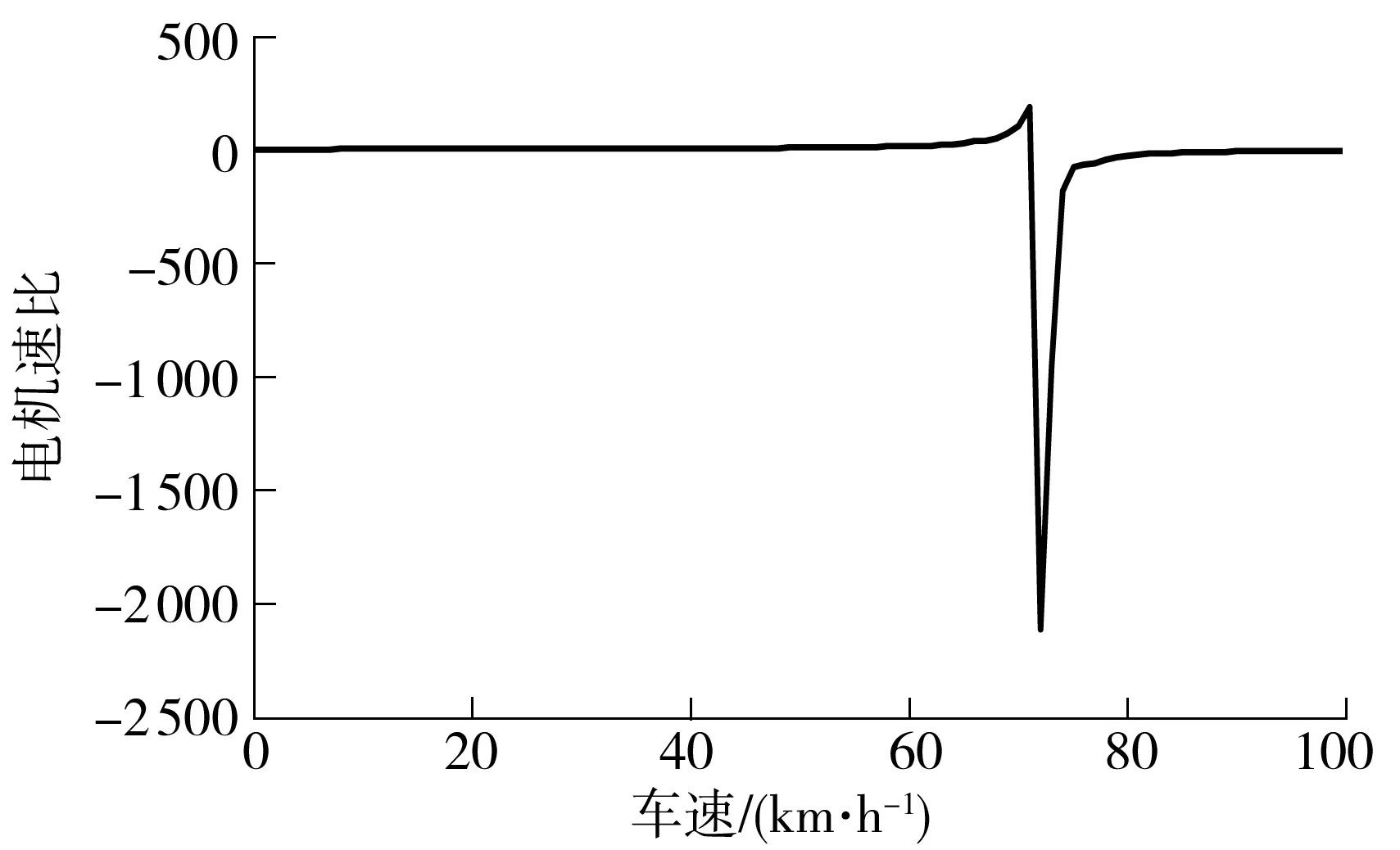
图12 传动比变化曲线

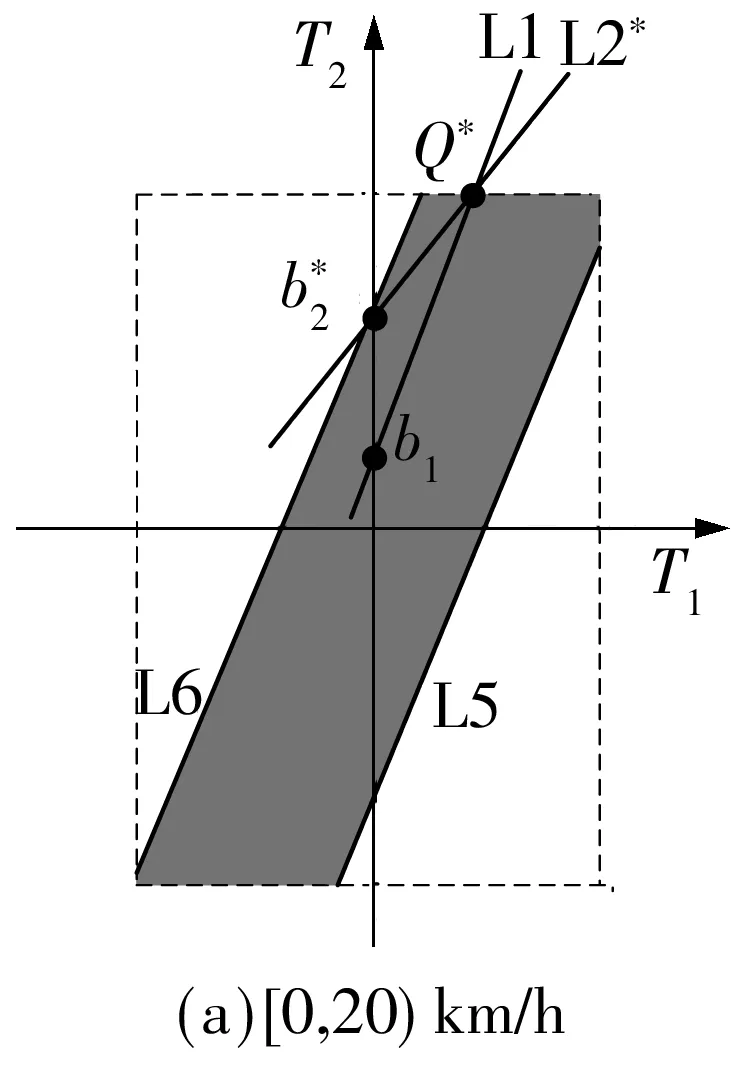
图13为全油门加速过程的T-T图.图13(a)对应于[0,20]km/h车速区间.在该车速区间，由式(21)和(22)，得系统输出转矩如下：

(42)

全油门加速过程中，为配合转矩，当电机E1转矩不受限时，系统输出转矩取决于电机E2转矩和发动机转矩，若二者转矩都取最大值，则系统输出转矩最大.全油门加速过程中，电机E2转速在3 000r/min以内，由图5可知，其转矩上限为200N·m.全油门加速过程前期，电机E2均能以200N·m输出，系统输出转矩取决于发动机输出转矩，故在[0,20)km/h车速区间，通过快速提升发动机转速可提高发动机最大转矩，有利于系统动力输出.在该车速段，整车储备功率充足而车速较低，整车驱动需求功率较低，故未能充分利用动力电池助力功率，发动机的部分功率则用于动力电池充电.

图13(b)所示为[20,50)km/h车速区间的T-T图.在该车速区间，发动机高转矩输出，即截距b1相比图13(a)中的上移.电机E2工作在外特性，即Q*处于电机E2的转矩上限，电机E1配合系统转矩输出.由于电机E1转速较高，该车速区间的极限转矩显著减小.该过程通过缓慢提高发动机转速来提高整车驱动功率，并控制电机速比，防止电机E1转速上升导致电机E1转矩范围收窄，限制系统动力性输出.随着车速的提高，整车需求功率提高，动力电池逐渐由充电状态变为放电状态.

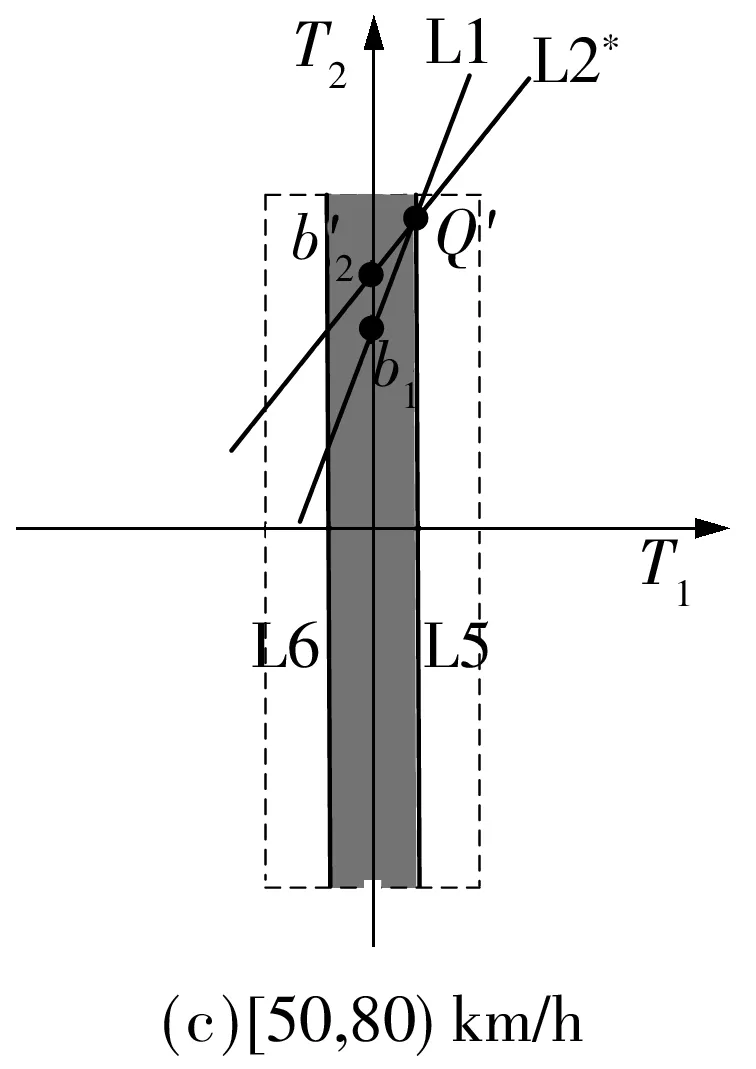
图13(c)所示为[50,80)km/h车速区间的T-T图.在该车速区间，电机E2在零转速附近，电机速比迅速增大，电机E1转速较高，所以功率带收窄，动力电池功率限制系统动力输出，电机E2转矩下降，系统输出转矩下降.由于发动机在高转速区间，其最大输出转矩变化小，即直线L1基本不变，而在电机速比变化过程中，功率带旋转，导致直线L2′截距缓慢下降.所以电机E2转矩呈逐渐下降趋势(见图8)，转矩波动由电机额外功率损耗的非线性特性以及发动机加速度波动造成.该过程需合理控制发动机转速，保持电机E1工作在极限转速附近.由于处于控制临界点，所以在该车速段发动机加速度控制曲线波动明显，如图6所示.

图13(d)所示为[80,100)km/h车速区间的T-T图.在该车速区间，通过维持发动机高转速保持发动机以高功率输出.而随着车速上升，电机E1转速逐渐下降，有利于扩张功率带，使直线L2保持高位，维持系统的大转矩输出.

4 整车试验验证与分析

根据动态规划仿真控制策略结果，提取发动机转速控制曲线为目标控制曲线，在工程样车上进行动力性能试验[16].

优化前后的区别在于发动机转速控制方式的不同.优化前，发动机转速按照原有Map由整车车速与油门踏板得到目标发动机转速以拉升发动机转速;优化后，根据动态规划仿真所得的发动机转速控制曲线拉升发动机转速.优化前后，由于油门踏板开度均为100%，所以发动机目标转矩均为外特性.

图14所示为优化前后发动机的转速曲线.在[10,80]km/h的车速区间，优化前发动机的转速远低于仿真目标.经过优化，在低速区间快速拉升发动机转速逼近仿真目标转速，使得[10,40]km/h区间内发动机以仿真目标转速运行.实际控制中，由于整车阻力较大，若发动机在(40,90]km/h区间内以仿真目标转速运行，将导致电机E1转速超出最大转速，存在电机烧毁风险，故在(40,90]km/h区间，优化后发动机转速低于仿真目标且高于优化前转速.在(90,100]km/h区间，发动机实际功率随着转速明显增加，由双电机转矩图可知，这有利于提高系统动力性，故继续拉升发动机转速.

图14 优化前后发动机的转速曲线

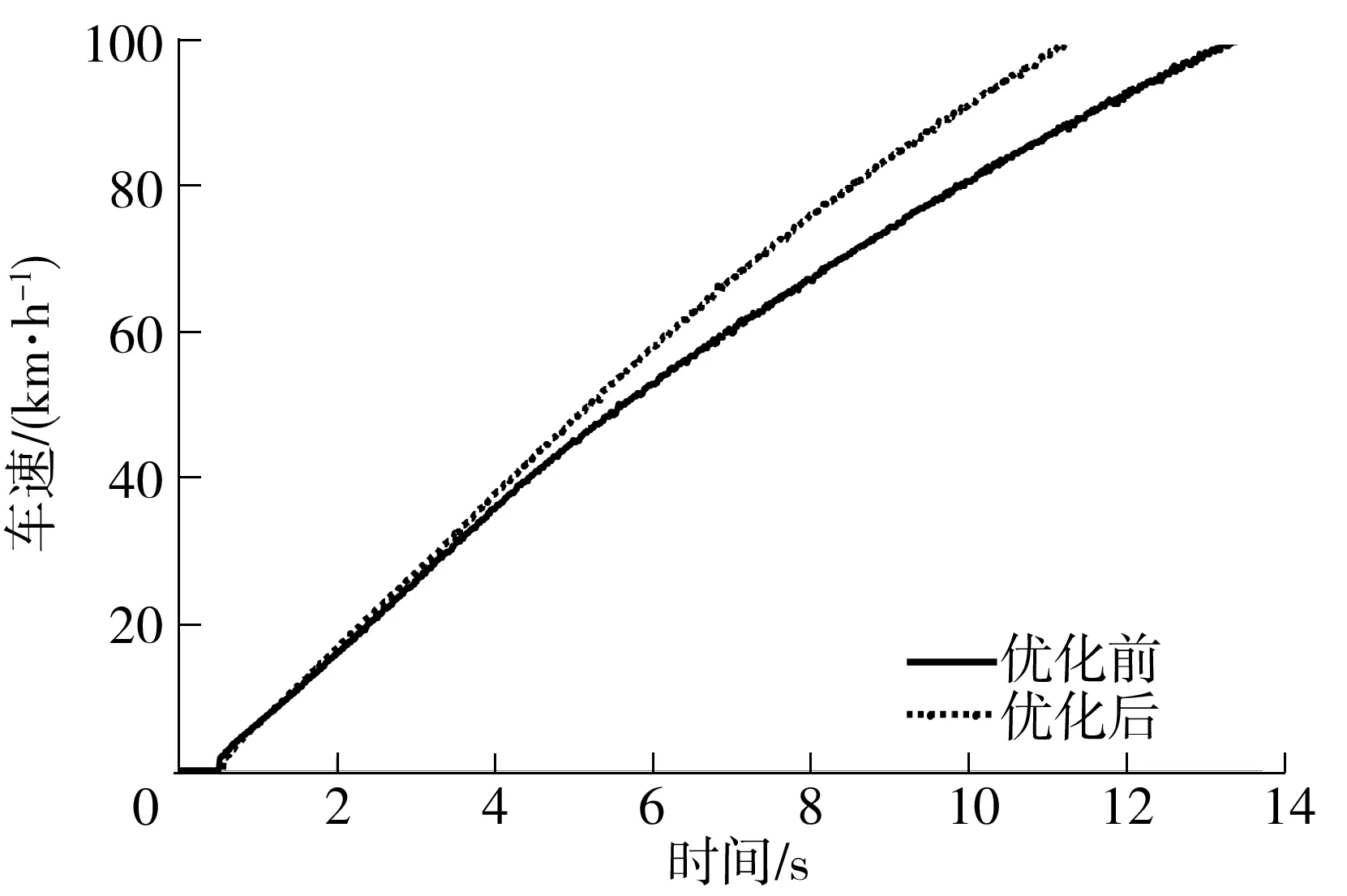
图15 优化前后的整车车速曲线

图15所示为优化前后的整车车速曲线.优化后百公里加速时间从13.4 s缩短至11.3 s.通过发动机转速控制优化，百公里加速时间减少15.7%.以仿真所得发动机转速曲线优化发动机转速控制策略，有效地提高了动力性.

5 结语

文中针对新型功率分流混合动力系统进行了数学建模，以车速为序列将全油门加速过程划分为一个多级决策过程，以发动机转速为状态变量、发动机加速度为控制变量、百公里加速时间为代价函数，应用动态规划算法求解了整车动力性优化问题.

基于仿真结果，文中归纳了全油门加速过程控制规律.忽略电机额外功率损耗和四轴转动惯量，建立了双电机转矩图，定义了电机速比及动力电池功率带，将百公里加速过程划分为4个阶段并归纳了各阶段对应的控制规律.同时，以动态规划仿真中的发动机转速控制曲线为控制目标曲线，应用所得控制规律进行了整车控制策略优化试验，结果表明，优化后百公里加速时间减少了15.7%，整车动力性显著提升.

文中以动力性为优化指标而不考虑对经济性的影响，在后续研究中，可通过选取适当的转化因子，并建立合理的代价函数，在优化动力性的同时优化经济性.

[1] Chan C C,Bouscayrol A,Chen K.Electric,hybrid,and fuel-cell vehicles:architectures and modeling [J].IEEE Transactions on Vehicular Technology,2010,59(2):589- 598.

[2] Zhang X,Mi C.Vehicle power management:modeling,control and optimization [M].London:Springer Science & Business Media,2011.

[3] Li W,Abel A,Todtermuschke K,et al.Hybrid vehicle power transmission modeling and simulation with simulationX [C]∥Proceedings of International Conference on Mechatronics and Automation,ICMA 2007.Harbin:IEEE,2007:1710- 1717.

[4] Ahn K,Papalambros P Y.Design optimization of motor/generator full-load characteristics in two-mode hybrid vehicles,SAE paper,2009- 01- 1317 [R].[S.l.]:SAE International,2009.

[5] Singer-Englar A,Kamisky R,Erickson P,et al.Design and development of a parallel hybrid powertrain for a high performance sport utility vehicle，SAE paper,2005- 01- 3827 [R].[S.l.]:SAE International,2005.

[6] Moore T C.Tools and strategies for hybrid-electric drivesystem optimization,SAE paper,961660 [R].[S.l.]:SAE International,1996.

[7] 周兵,江清华,杨易.两挡变速器纯电动汽车动力性经济性双目标的传动比优化 [J].汽车工程,2011，33(9):792- 797. Zhou Bing,Jing Qinghua,Yang Yi.Transmission ratio optimization with dual objectives of power performance and economy for a two-speed electric vehicle [J].Automotive Engineering,2011,33(9):792- 797.

[8] Han Z,Yuan Z,Guangyu T,et al.Optimal energy management strategy for hybrid electric vehicles [J].SAE Tran-sactions,2004,113(3):408- 417.

[9] Chen Z,Mi C,Xu J,et al.Energy management for a po-wer-split plug-in hybrid electric vehicle based on dynamic programming and neural betworks [J].IEEE Transactions on Vehicular Technology,2014,63(4):1567- 1580.

[10] Han Bing,Cai Yixi,Zhang Tong.Hydraulic system design for full hybrid transmission [C]∥Proceedings of the 2011 International Conference on Electric Information and Control Engineering (ICEICE).Wuhan:IEEE,2011:2256- 2259.

[11] Han Bing,Zhang Tong,Cai Yixi.Development of a single-mode full hybrid system [C]∥Proceedings of the 2011 International Conference on Electric Information and Control Engineering (ICEICE).Wuhan:IEEE,2011:2108- 2111.

[12] Wang D P,Li S M.Study on power balance control in full hybrid system [J].Applied Mechanics and Mate-rials,2011,143/144:259- 264.

[13] Yu H S,Zhang J W,Zhang T.Control strategy design and experimental research on a four-shaft electronic continuously variable transmission hybrid electric vehicle [J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2012,226(12):1594- 1612.

[14] Yu H,Zhang J W,Zhang T.Optimal control of one hybrid electric vehicle with four-shaft planetary power-split transmission [J].International Journal of Electric and Hybrid Vehicles,2012,4(2):161- 185.

[15] 冯樱.运用杠杆法计算汽车行星齿轮变速器的传动 [J].湖北汽车工业学院学报,2008,22(3):17- 20. Feng Ying.Analysis on the ratios of AT by lever method [J].Journal of Hubei Automotive Industries Institute,2008,22(3):17- 20.

[16] GB/T 19752—2005,混合动力电动汽车动力性能试验方法 [S].

Acceleration Performance Optimization of Novel Power-Split Hybrid Electric Vehicle

WangChen1GuoMing-lin2LiuGuo-zhi3

(1.Clean Energy Automotive Engineering Center，Tongji University，Shanghai 201804，China;2.School of Mechanical Engineering，Shanghai Jiaotong University，Shanghai 200240，China;3.Technology Development Department，Corun CHS Technology Co.，Ltd.，Shanghai 201501，China)

Acceleration performance is one of important vehicle performance indicators. In order to solve the optimization problem of acceleration performance of hybrid electric vehicle,the full-load acceleration progress is converted into the multi-level decision-making process according to vehicle speeds, and a solution scheme based on dynamic programming is put forward. Then, a model for the novel power-split hybrid vehicle is constructed, and a globally-optimized control strategy is obtained on the Matlab platform. Meanwhile, a dual-motor torque figure is established,in which both the motor speed ratio and the battery power band are defined to analyze the control strategy of full-load acceleration. The vehicle test results of acceleration performance optimization show that one-hundred-kilometer acceleration time after the optimization decreases by 15.7%, which means that the proposed control stra-tegy on the basis of dynamic programming can significantly improve the vehicle acceleration performance.

hybrid powertrain; acceleration control;hybrid electric vehicles;dynamic programming;optimization

2015- 03- 09

国家高技术研究发展计划(863计划)项目(2011AA11A207)；国家自然科学基金资助项目(51275355) Foundation items: Supported by the National High-Tech R&D Program(863 Program) of China(2011AA11A207) and the National Natural Science Foundation of China(51275355)

王晨(1986-)，男，博士生，主要从事混合动力变速器控制技术研究.E-mail： w_chen_ev@sina.com

1000- 565X(2015)11- 0096- 09

U469.72

10.3969/j.issn.1000-565X.2015.11.014