悬链线和大变形梁理论的J型铺设研究
2015-04-18康庄张立张翔
康庄,张立,张翔
(哈尔滨工程大学 船舶工程学院 深海工程技术研究中心,黑龙江 哈尔滨150001)
悬链线和大变形梁理论的J型铺设研究
康庄,张立,张翔
(哈尔滨工程大学 船舶工程学院 深海工程技术研究中心,黑龙江 哈尔滨150001)
为获得J型铺设解析方法,研究了深水钢悬链立管的J型铺设作业过程中的静力分析,引入一种称为分段力学模型的优化模型。首先基于悬链线理论建立悬链线模型进行求解,然后在悬链线模型的基础上对立管进行分段计算,变形大的区域使用大变形梁理论,依据奇异摄动法渐近展开二阶非线性微分控制方程,其余区域使用悬链线理论重新求解,最后合成两部分结果为整体解。与悬链线理论和大变形梁理论对比分析之后发现,分段力学模型对边界条件满足较好,计算结果与高精度的大变形梁理论结果相当。同时,使用分段力学模型来分析了湿重以及刚度的参数敏感性影响。
钢悬链立管;J型铺设;悬链线;大变形梁;摄动法;分段力学模型
立管系统作为连接海上浮体与水下生产系统的关键性部分,是海洋开发中不可或缺的组成部分,其中钢悬链立管(steel catenary risers, SCR)以其良好的适用性以及低廉的价格成为立管系统的首选形式[1],铺设深度也从浅水走向3 500 m以上的超深水。与S型铺设和卷筒铺设方法相比,J型铺设,以立管近乎垂直下放到水中的形态而得名,能够使钢悬链立管产生更小的应力,成为超深水立管铺设中的最优选择。有以下优点:1)缩短安装船与触地点(touch down point,TDP)之间的距离;2)有效降低安装船对立管的水平支撑力,进而降低了立管的应力;3)消除了立管在托管架附近上弯段的弯曲;4)减小了安装船所提供的拉力的要求,无需脆弱的托管架[2];5)除了接近海面的一小段区域外立管受波浪影响很小[3]。J型铺设过程中钢悬链立管的铺设形态和受力分析是立管总体设计的重点,一方面关系到钢悬链立管的安全性能,决定了立管在自重和张紧器作用下的静张力和弯矩,另一方面静力分析更是动力分析的初始平衡位置[4]。
立管J型铺设分析中,悬链线理论、有限元和有限差分法是常用到的方法:悬链线理论忽略了立管的弯曲刚度,有限元和有限差分法[5]离散了立管结构带来了结果的不精确,与钢悬链立管的实际受力有一定的不同,而大变形梁理论则能够充分把握受力的最主要特点[6],国际上有不少学者[2,4-10]提出了基于大变形梁理论的解析方法。
R.PLUNKETT[7]建立了大变形梁理论的受力非线性微分方程,利用奇异摄动法渐进展开,对立管受力求解。D .A .DIXON等[8]对原有的悬链线理论加以改进,引入了刚性悬链线理论进行管道铺设形态分析,并尝试用数值方法迭代求解。F. Guarracino等[9]研究了S型铺设的立管弹性变形,考虑了立管弯矩影响、立管横截面的变形,以及立管在水中的内压和外压影响,修正弯矩表达,通过使用奇异摄动法,获得立管S型铺设的解析解。S.Lenci 等[2]从经典悬链线微分方程出发,提出了3种阶梯状的不同形式的简化模型,解决不同边界条件下的求解,但是其可靠性和安全性有待验证。Torselletti等[10]基于大变形梁理论分析S型铺设过程中管线悬垂段的应力。王琴等[4]基于大变形梁理论,对J型铺设研究,并利用奇异摄动法求解,得到J型铺设过程中的弯矩和顶部张力。然而,大变形梁理论虽然求解精度较高,但是计算过程针对于高阶非线性方程复杂,计算量较大,其在计算J型铺设时,假设立管顶端的弯矩为零,这与工程实际有一定的误差,另外,悬垂段使用大变形梁理论分析并不必要。
本文在前人研究的基础上,对立管的大变形梁理论模型进行改进,提出“分段力学模型”:先对立管整体使用悬链线理论计算得到其一般初始形态,找到立管上曲率小于某值λ的分段点E,然后在垂弯段使用大变形梁理论,通过摄动法得到解析解,自分段点至立管顶部分离点使用悬链线模型重新求解,进而合成两部分解得到整体解。
1 J型铺设的静力分析
在深水铺设过程中,立管要受到多种力的复杂作用,其中主要为自身重力、浮力,以及水动力的影响,为了建立模型对J型铺设进行静力分析,做出以下合理假设:1)立管在变形时候不产生扭矩;2)立管是细长体,可以简化为梁单元;3)海床是刚性的,忽略立管的剪切变形和轴向变形。
为了更好地对钢悬链立管进行静力分析,本文使用了两个逐步近似的悬链线模型和分段力学模型。后者在前者的基础上,对立管整体使用分段计算:触地点附近使用大变形梁理论,弯曲变形较小的区域使用悬链线模型。
1.1 悬链线模型
深水J型铺设中,悬链线模型是描述J型铺设的最简单的形式,它忽略了弯曲刚度,只承受轴向拉力,在假设条件下,模型可简化为固定平面内的二维模型,如图1所示。在该分析模型中,模型的原点O建立在触地点TDP,该点是立管从海床脱离的位置;x轴是水平轴,正向沿着管线伸展的方向;D是最大海水深度,即海床所在水深;l表示立管顶端的水平位置,微元承受的张力为T(x),单位长度立管的湿重为w。
悬链线的控制方程为
(1)
式中:δ=w/H,考虑触地点TDP处的边界条件:
(2)
当海床坡角为0o,有
(3)
同时,考虑到铺管船位置的边界条件:y(l)=D,y′(l)=tanφ(φ由J型塔控制),可得任意位置与水平方向夹角、曲率以及张力如下:
(4)
(5)
(6)
虽然在微元力学模型中并没有计入弯曲刚度影响,但是近似的弯矩仍然可以通过将抗弯刚度乘以管线的曲率得到:
(7)
悬链线模型主要优点是:1)概念上较为简单;2)计算结果不复杂,便于工程应用;3)能够给出悬垂段的可靠结果;4)对于更高精度的解析模型或者数值模型,能够给出一个初始值,便于其使用;5)当抗弯刚度越小,该模型的结果越精确[2]。悬链线模型建立在对于管线受力极大限度简化的基础之上,主要缺点是在触地点TDP附近的不精确,而对于深水J型铺设而言,TDP附近的求解是非常重要的。
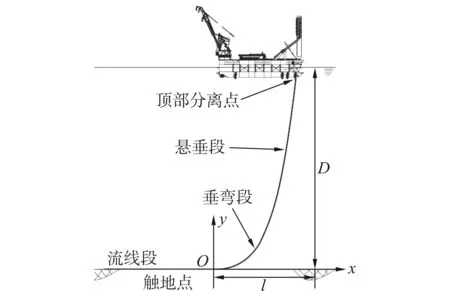
图1 J型铺设示意图Fig. 1 Configuration of J lay installation
1.2 分段力学模型
在利用1.1中悬链线模型得到SCR的解之后,立管的曲率从O点(TDP)到分离点A逐渐下降,在κ(x)函数曲线上,点E处κ(x)=λ,且OE段曲率变化迅速,EA段曲率变化平缓。图2分别对OE和EA的微元描述如下。图中,H,V分别表示微元在水平和竖直方向的受力,M表示微元所受弯矩,θ表示与水平方向的夹角,w表示单位微元在水中的湿重,f(s)表示单位微元所受的流体力。

图2 分段力学模型形态和受力示意图Fig. 2 Configuration and forces diagram of piecewise mechanics model
1.2.1OE段
f(s)sinθ·ds=0
(8)
根据弯矩剪力的微分关系:M=EIdθ/ds将微元当作梁单元处理,则I为常数,dM/ds=EId2θ/ds2,显然水平力H=C,且dV/ds=w。
对于θ有:dy/ds=cosθ,dx/ds=sinθ,深水铺设过程中,f(s)/w≪1 ,因而f(s)≈0可以忽略。则微分方程可以写成:
(9)
式(9)大变形梁理论控制方程是典型的二阶非线性方程,且由于其边界可动,此类问题常用奇异摄动理论进行求解。本文采用匹配渐进展开法,借助Wasow的研究,使用VanDyke匹配原则,在O点(TDP)和E点邻域使用内场展开,对于其余部分使用外场展开。
主要求解过程如下:
1)控制方程的无量纲化

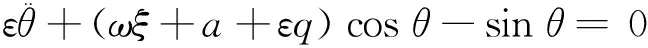
(10)

2)一般区域的外场展开
将θ(ξ,ε) 展成关于ε的幂级数:
(11)
则
(12)
展开并使ε各次幂系数为0,可得θk(ξ)的各阶递推方程,前三阶方程表示为
ε0阶
(13)

(14)
ε1阶
(15)
由式(13)~(15),解得方程(10)的二阶外场展开解为:
θo(ξ,ε)=arctan(ωξ+a)+
(16)

显然,此外场解对ξ=0,1 的2个边界层区域内不适用,因此需分别建立两边界层内的内场近似解。
3)ξ=1 端的内场展开
(17)
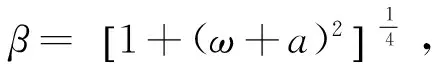
(18)

(19)
与外场解求解过程类似,将方程(19)代入式(18)并展开,使ε各次幂系数为0,获得φ的各阶递推方程。考虑ξ=1 处的边界条件:
(20)
则
(21)
式中:τ为无量纲曲率。
利用边界条件(21)求解各阶递推方程,同时,运用VonDyke匹配原则,即n项外部展开式的m项内部展开式等于m项内部展开式的n项外部展开式,确定递推方程中积分常数。这里取m=n=2。可得θ在ξ=1 端的二阶内场展开解为
(22)

4)TDP附近(ξ=0 端)的内场展开

(23)

(24)
考虑TDP点边界条件,为保证弯矩的连续性,选择曲率边界条件,有:
(25)
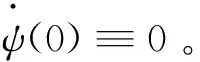
利用边界条件求解递推方程,同时利用VonDyke匹配原则,确定积分常数,仍取m=n=2。
得θ在ξ=0 端的二阶内场展开解为:
(26)
5)合成渐进展开解

(27)
后两项分别表示ξ=0及ξ=1端边界处外场解的内场极限。将内场解统一为外场变量,有:
θC(ξ,ε)=arctan(ωξ+a)+
(28)
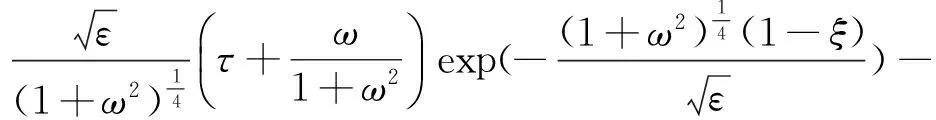
(29)
6)其他参数的获得
为得到管线弯曲形态,需获得曲线各点的横纵坐标。由式(29)得到:
同理,大变形梁总长L可表示为:
(30)
注意,L是利用大变形梁理论重新求解后的结果,与1.1节中提供的初值有区别。
考虑端点E受力情况,如图3所示。

图3 分段点E点受力分解Fig. 3 Components of the force acting on point E
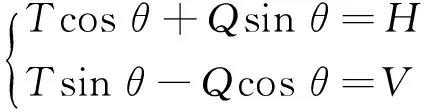
(31)
则轴向张力可表示为
T=Hcosθ+Vsinθ
(32)
(33)
1.2.2EA段
当OE段使用大变形梁理论计算出结果之后,根据E点的形态和弯矩连续作为边界条件,利用1.1节中悬链线模型重新计算得到EA段的结果。得到钢悬链立管的形态、轴向张力、弯矩等参数之后,冯米塞斯应力计算原理可以计算出立管的等效应力等参数。
1.2.3 分段力学模型的优点
1)计算精度高,与悬链线模型相比,不受抗弯刚度EI影响;2)在曲率较大影响的区域,充分考虑了弯矩影响;3)相对于全部使用大变形梁理论的摄动法求解,分段力学模型求解非线性方程区域缩小,具有计算效率高的特点;4)不需要假设顶端未知条件;5)为包含大变形和小变形的结构,如S型铺设、缓波和陡波形SCR和柔性立管的求解提供了解决思路。
2 数值求解
钢悬链式立管J型铺设分段力学计算模型的计算流程如图4所示。
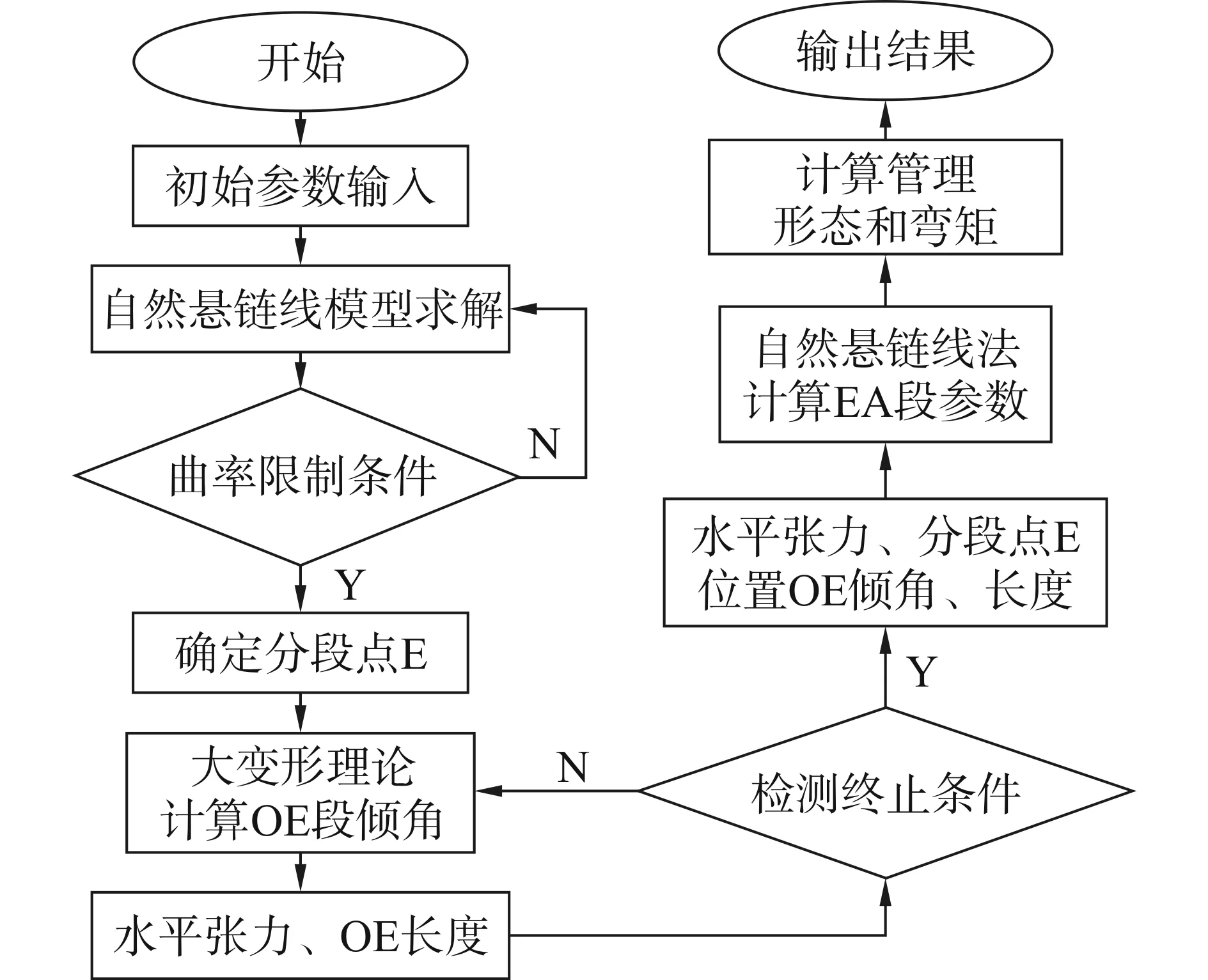
图4 计算流程图Fig. 4 Flowchart of calculation
求解过程叙述如下:
1)输入初始参数;
2)确定分段点E位置,OE初始长度L0;
3)匹配渐进展开法求解OE段,具体过程为:
①确定方程参数ε的初始值,得到新参数ε;
4)重新对EA段采用悬链线理论求解;
5)将两部分力学模型的结果进行综合,得到J型铺设全长范围内的挠曲线形态以及弯矩等参数。
3 算例分析
为了验证悬链线模型和分段力学模型的合理性,使用算例进行分析,J型铺设进行计算,钢材选取为X65钢,密度为7 850 kg/m3,海床倾角为0,其余数据根据API规范设定。计算程序基于MATLABVersion7.10,画图使用Origin8.0。
3.1 模型对比
管径为18英寸,壁厚1.25英寸,作业水深为3 000m,管线总长为4 000m,预张力为5 681kN。悬链线理论、大变形梁理论和分段力学模型对形态和弯矩的计算结果如图5和6所示。

图5 3种模型的形态计算结果Fig. 5 Configuration of three models

图6 3种模型的弯矩计算结果Fig. 6 Bending moment of three models
根据图5,三者形态计算结果相似,仅在顶部附近出现较小偏差,详细数据如表1所示,大变形梁理论和分段力学模型对悬垂段和分离角都有较好的符合。在图6中,悬链线理论计算出的最大值大于大变形梁理论和分段力学模型的结果,最大值出现位置与后两者略有差距,且在触地点TDP位置出现弯矩不连续,由于底端受海床约束,浮体响应以及海流诱发的立管涡激振动容易导致SCR触地点区域的疲劳破坏[11],而触地点区域的动力响应主要决定了钢悬链线立管的可行性[12],故悬链线理论受到极大局限。而后两者在除立管顶端分离点以外的计算结果近似重合,证明分段力学模型是合理的;实际铺设过程中立管从J型塔分离要产生一定弯矩,大变形梁理论假设顶端弯矩为零不但不合实际,且导致其结果在顶部分离点附近出现弯矩突变。分段力学模型由于在垂弯段使用的是可控的曲率作为边界条件,在悬垂段使用的是分段点的形态和弯矩的连续作为边界条件,避免了不合理假设带来的误差。

表1 3种模型的计算数据
注:0 m自井口算起,下同;分离角是立管与竖直方向的夹角。
3.2 湿重
本质上,立管尺寸的变化是湿重和刚度的变化,因而根据API规范,选取相应类型的立管作为分析算例。图7、8中给定的湿重分别是1.50、1.55、1.60、1.65、1.70 kN/m。
图7显示随着湿重的增加,TDP位置不同,立管从J型塔的顶部分离点与TDP的距离减小。图8表明立管弯矩从TDP迅速增加到最大值后减小,而随着湿重的增加,TDP附近的最大弯矩的值随之增加,详细计算结果如表2所示。

图7 不同湿重的形态计算结果Fig. 7 Configuration of different wet weights
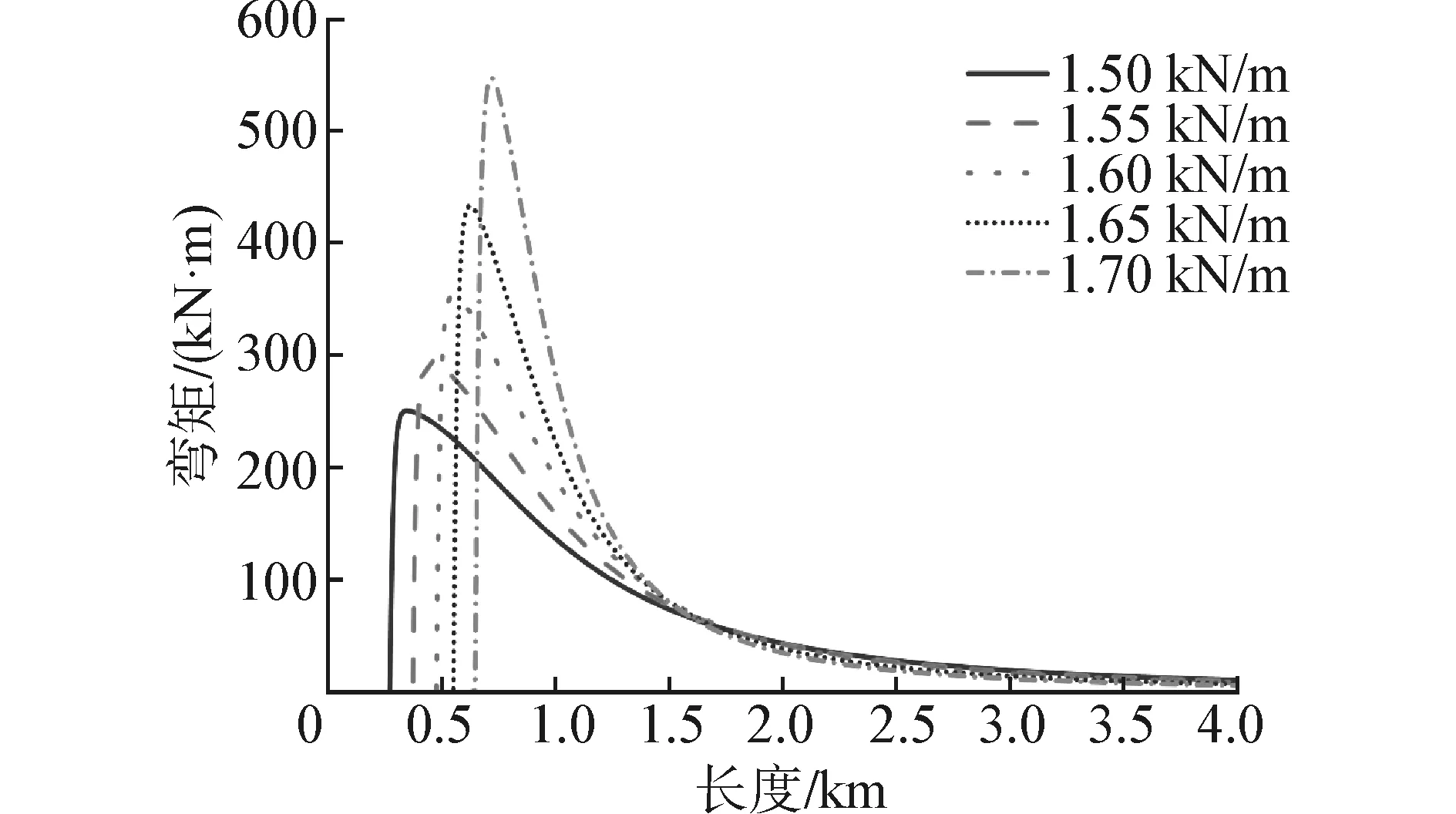
图8 不同湿重的弯矩计算结果Fig. 8 Bending moment of different wet weights
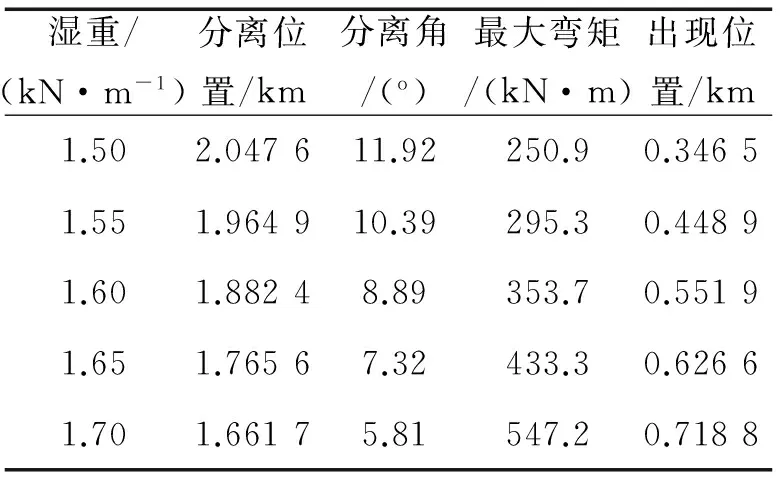
表2 不同湿重计算结果
3.3 刚度
不同刚度时的形态和弯矩计算结果如图9和10所示,刚度EI分别是1.0×108、1.5×108、2.0×108、2.5×108、3.0×108N·m2。
图9 不同刚度的形态计算结果Fig. 9 Configuration of different bending stiffness

图10 不同刚度的弯矩计算结果Fig. 10 Bending moment of different bending stiffness
根据图9和表3,5者的形态十分相近,立管从铺管船J型塔的分离位置和分离角近似相同;根据图10,弯矩的最大值随着刚度的增加而增加。

表3 不同刚度计算结果
4 结论
1)基于悬链线理论和大变形梁理论的“分段力学模型”在TDP附近能够很好地与大变形梁理论的结果吻合较好;在悬垂段,由于立管的曲率不大,分段力学模型能够与悬链线理论和大变形梁理论结果较好近似,同时兼具悬链线理论和大变形梁理论的优点,并且有效回避了二者的缺点,计算过程较大变形梁理论简单,是一种合理的优化模型,证明其高效高精度合乎工程实际,其计算结果可以为钢悬链立管J型铺设提供预报。
2)算例结果表明,分段力学模型与大变形梁理论精度相当。分段力学模型与大变形梁理论的结果吻合较好,特别在TDP位置;对比不同湿重和刚度的结果后,发现湿重和刚度对计算结果影响明显。
3)分段力学模型经过扩展后可以为包含大变形和小变形结构如S型铺设、缓波和陡波形SCR和柔性立管的解析求解提供一种思路,延拓了单一悬链线理论和大变形梁理论的使用范围。
[1]宋儒鑫. 深水开发中的海底管道和海洋立管[J]. 船舶工业技术经济信息, 2003(6): 31-42. SONG Ruxin. Pipelines and risers for deepwater developments[J]. Technology and Economy Information of Ship Buildings, 2003(6): 31-42.
[2]LENCI S, CALLEGARI M. Simple analytical models for the J-lay problem[J]. Acta Mechanica, 2005, 178(1/2): 23-39.
[3]安德鲁 C 帕尔默, 罗杰 A 金. 海底管道工程[M]. 2版. 梁永图, 译. 北京: 石油工业出版社, 2013: 176-177.
[4]WANG Qin, DUAN Menglan, LI Haiming, et al. A singular perturbation method for parametric investigation on J-lay installation of deepwater pipelines[J]. China Ocean Engineering, 2013, 27(6): 751-766.
[5]SANTILLAN S T, VIRGIN L N. Numerical and experimental analysis of the static behavior of highly deformed risers[J]. Ocean Engineering, 2011, 38(13): 1397-1402.
[6]CALLEGARI M, CARINI C B, LENCI S, et al. Dynamic models of marine pipelines for installation in deep and ultra-deepwaters: analytical and numerical approaches[C]//Proceedings of the 5th National Congress of the Italian Association of Mechanics (AIMETA). Ferrara, 2003.
[7]PLUNKETT R. Static bending stresses in catenaries and drill strings[J]. Journal of Engineering for Industry, 1967, 89(1): 31-36.
[8]DIXON D A, RUTLEDGE D R. Stiffened catenary calculations in pipeline laying problem[J]. Journal of Engineering for Industry, 1968, 90(1): 153-160.
[9]GUARRACINO F, MALLARDO V. A refined analytical analysis of submerged pipelines in seabed laying[J]. Applied Ocean Research, 1999, 21(6): 281-293.
[10]TORSELLETTI E, VITALI L, LEVOLD E, et al. Submarine pipeline installation JIP: strength and deformation capacity of pipes passing over the S-lay vessel Stinger[C]//25th International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2006: 227-235.
[11] 王坤鹏, 薛鸿祥, 唐文勇. 基于全耦合模型和管土作用模型的深海悬链线立管触地区域疲劳特性分析[J]. 上海交通大学学报, 2014, 48(4): 576-582. WANG Kunpeng, XUE Hongxiang, TANG Wenyong. Fatigue characteristics analysis of steel catenary riser near touchdown zone based on full coupled model and SCR-soil interaction model[J]. Journal of Shanghai Jiaotong University, 2014, 48(4): 576-582.
[12]李艳, 李欣, 罗勇, 等. 深水钢悬链线立管 (SCR) 的设计与研究进展[J]. 中国海洋平台, 2013, 28(2): 6-13. LI Yan, LI Xin, LUO Yong, et al. Review of the design and research on deepwater steel catenary riser[J]. China Offshore Platform, 2013, 28(2): 6-13.
Analysis of J lay installation of a steel catenary riser based on catenary and large deflection beam theory
KANG Zhuang,ZHANG Li,ZHANG Xiang
(Deepwater Engineering Research Center, College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)
In order to obtain an analytic method for J lay installation, a static analysis was made of the J lay installation process of a deepwater steel catenary riser, then introduced an optimized model called the piecewise mechanics model. First the catenary model based on the catenary theory was established and solved. Then the riser was computed piece by piece, based on the catenary model, applying large deflection beam theory for the area with large deformation, and developed asymptotically the 2nd-order nonlinear differential control equation on the basis of a singular perturbation equation. This process was repeated using catenary theory for the remaining areas. Last, the results of the two parts were combined into an overall solution. A comparison of the piecewise mechanics model with the catenary riser theory and large-deflection beam theory, shows that the piecewise mechanics model meets the boundary conditions very well, the computation result matches the result of high-precision large-deformation beam theory. The piecewise mechanics model can also be used to analyze the influence of wet weight and stiffness on parameter sensitivity.
steel catenary riser; J lay; catenary method; large deflection beam; perturbation; piecewise mechanics model
2014-06-23.
时间:2015-07-15.
国家科技重大专项基金资助项目(2011ZX05027-002-004-008).
康庄(1978-), 男, 副教授; 张立(1991-), 男, 硕士研究生.
张立,E-mail:vzhangli@hrbeu.edu.cn.
10.3969/jheu.201407009
O312.2
A
1006-7043(2015)09-1170-07
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.U.20150715.1727.004.html
