改进的模拟退火算法在放射形专用线取送车优化中的应用

2015-04-18吴艳群

武汉理工大学学报（交通科学与工程版） 2015年6期

董鹏吴艳群

（兰州交通大学交通运输学院兰州 730070）

0 引言

在较大的铁路货运站、技术站和大型企业铁路专用线的各种运输作业中，取送车作业都是非常重要的工作，其效率高低直接关系到车辆周转率和货物送达的速度，进而影响企业的经营效益.因此，对取送车作业进行优化，能够有效缩短车列的停留时间，加速车辆周转率，对于提高运输效率和企业的经济效益意义重大.

铁路专用线按装卸作业点的不同布置形式，分为放射形和树枝形2大类［1］.本文主要讨论放射形专用线取送车优化问题.宋建业等［2－3］采用表上移动法以取送同序方案为初始状态，通过在方案计算表上移动相邻送车顺序或取车顺序，使各作业地点中断时间的最大值降低到最小程度，从而得到一个最优取送顺序方案，方法相对易于实现.王慈光等［4］针对该问题给出了送车需要时间和取车需要时间的计算公式，并用送车增量和取车增量替代目标函数简化计算.用分部求解的思路寻求最佳取送方案，本质是在送车状态树上采用隐枚举法进行搜索.牟峰、王慈光等［5－6］将取送车作业作为一个系统进行整体考虑，以货车在站停留的总车小时消耗最小为优化目标，建立了数学模型，并采用基于云模型的参数自适应蚁群遗传算法进行求解.上述若干文献对问题本身的研究透彻，建立的数学模型成熟，后期的研究则主要集中于智能优化算法的设计和仿真分析，力图提高计算速度.文献［7］设计了单亲遗传算法，文献［8］提出了一种基于遗传算法信息素更新策略的改进蚁群算法，并结合算例进行仿真，也都取得了较好的效果.

本文针对放射形专用线直达车流取送车问题设计了一种专门的模拟退火算法，并结合算例进行仿真和分析.

1 问题描述与分析

放射形专用线的布置图形可抽象为图1，其中节点0为货运站，节点1，2，3分别为3条专用线.放射形专用线直达车流取送车问题可描述为：若干直达列车整列到达货运站（节点0）后，首先在货运站解编成车列；然后由一台调车机车将其中一个车列由货运站送往对应的专用线，到达专用线后将车列摘下进行装卸作业，调车机车立即返回货运站，这就完成了一次送车作业；重复执行上一步，直到所有车列都送往专用线为止，这一过程称为送车过程；接下来开始取回车列，调车机车从货运站开到最先完成装卸作业的专用线，连挂车列并返回货运站，完成一次取车作业；重复执行上一步，直到所有车列都取回到货运站为止，这一过程称为取车过程.

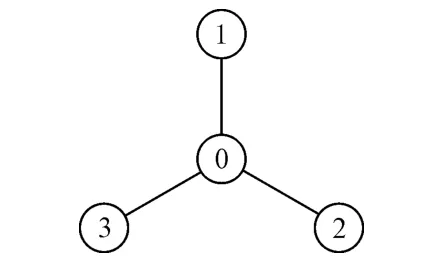
图1 放射形专用线示意图

放射形专用线的布置形式决定了调车机车每次将一车列由货运站送到专用线后，必须返回到货运站，才能开始送下一车列.取车过程也是一样.通常取送车作业只由一台调车机车完成.按节点1→2→3的顺序送车过程见图2a），按节点2→1→3的顺序取车的过程见图2b）.

图2 送车和取车实际径路

定义I为专用线集合，I＝｛1，2，3，…，n｝.其中：n为是专用线的最大数量.

衡量取送车作业的好坏必须考虑如下3种时间耗费.

1）装卸作业时间Li各专用线的装卸作业所需时间各不相同，用Li表示，i∈I.

2）取送作业时间Ti一次完整的送车作业包括调机连挂车列自货运站开往专用线和调机单机自专用线返回货运站2个单程，而取车作业也同样包括2个单程.一般将每个单程所需时间认为相等，因此取车作业时间和送车作业时间也相等.设调机自货运站开往专用线i的所需单程时间为ti，那么：调机完成一次取车或送车作业的时间Ti＝＝2ti，i∈I，通常：Li≫Ti.

3）调机等待时间Wi当全部送车作业完成之后，只有其中一条专用线完成装卸作业之后调机才能开始取车作业，因此可能需要调机等待装卸作业完成，这一时间称为该专用线的调机等待时间，用Wi表示，i∈I.假如某货运站有两条专用线，取送作业和装卸作业所需时间见表1，那么调车机车按先1后2的顺序送车，就会在到专用线1取车之前产生调机等待时间W1.

图3为取送车作业时序.图中方块1～10表示调车机车往返过程，0～60min为送车过程，80～150min为取车过程.其中白色方块5（60～80 min之间）是全部送车任务结束后，要等待专用线1完成装卸作业而耗费的时间W1（方块上方画有虚线箭头），白色方块8（100～110min之间）表示为等待专用线2完成装卸作业而耗费的时间W2.由图3可见，调车机车只需要在一条专用线装卸作业完成之时赶到即可，而不是等装卸作业完成之后才去取车.所以图中1号专用线的装卸作业从车列送达后开始，送车过程真正提供的装卸作业时间只有＝t＋2t（10～60min之间），12但取车过程又可以提供时间（80～90min之间），加起来正好是T1＋T2＝2（t1＋t2）.

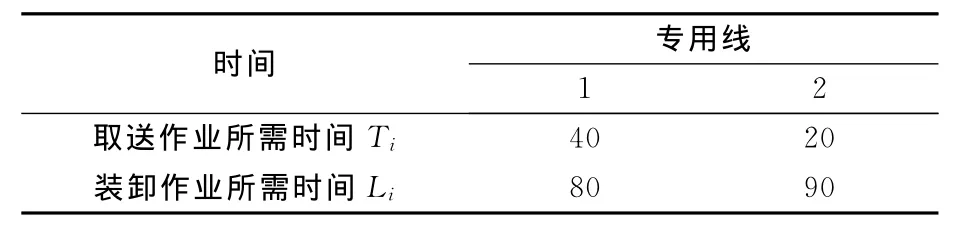
表1 2条专用线的各项作业所需时间 min

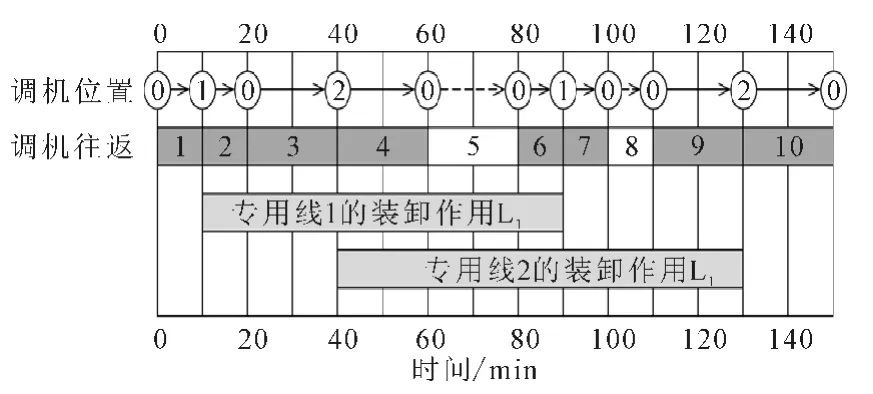
图3 取送车作业时序图

放射形专用线直达车流取送车问题的优化目标只能是各种作业时间之和最小，而不可能是取送车走行路径最短.因为对每条专用线来说，调车机车取送各一次，路径长度是固定的.在3种作业时间中，装卸作业时间由装卸任务和装卸能力决定，由于装卸能力通常是稳定的，所以一个装卸任务所需的装卸时间是固定的；取送作业所需时间由取送作业走行长度和机车走行速度决定，在线路条件和机车类型没有较大改进的情况下也不会有太大变化；只有调机等待时间会由于取送车顺序的不同而有所不同.因此最好的取送车方案是使调机等待时间最小的方案，而这与送车顺序和取车顺序密切相关.

下面根据实例建立调机总等待时间（见表2～表5）的计算公式.现有如下货运站，共4条专用线，分别用1，2，3，4进行编号，即I＝｛1，2，3，4｝.

送车顺序用S（s1，s2，s3，s4）表示，如果有4条专用线，送车顺序为4－1－2－3，则s1＝4，s2＝1，s3＝2，s4＝3，即 S＝（4，1，2，3）.取车顺序用Q（q1，q2，q3，q4）表示.

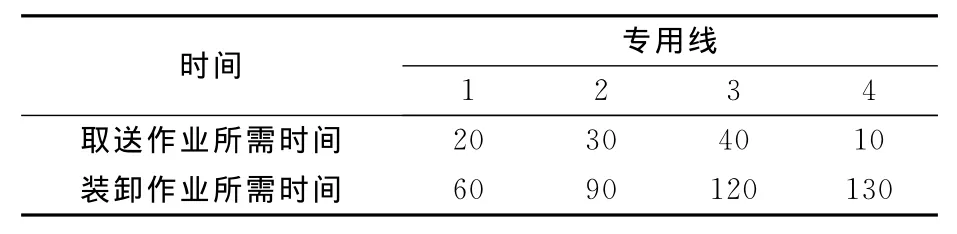
表2 4条专用线的各项作业所需时间 min

送车过程为各专用线所提供的装卸作业时间为θsi：

各专用线还需要的装卸作业时间为φsi

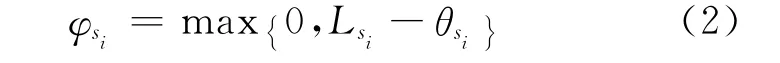
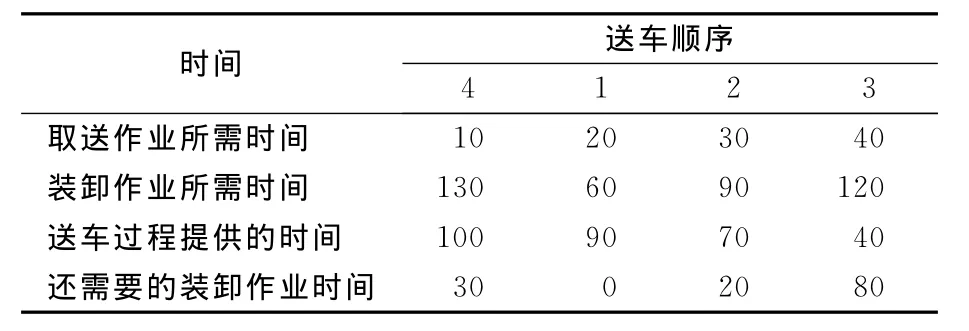
表3 送车顺序为4－1－2－3时还需要的装卸作业时间min

对于任意的取车顺序Q（q1，q2，…qn）：

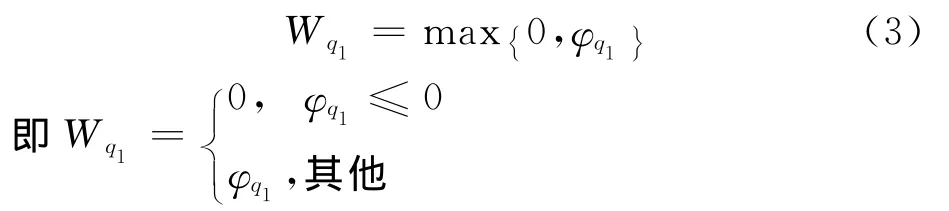
也就是说，对于要去取车的专用线如果还没有完成装卸作业，调机就必须等待一段时间；否则等待时间为0.同理：

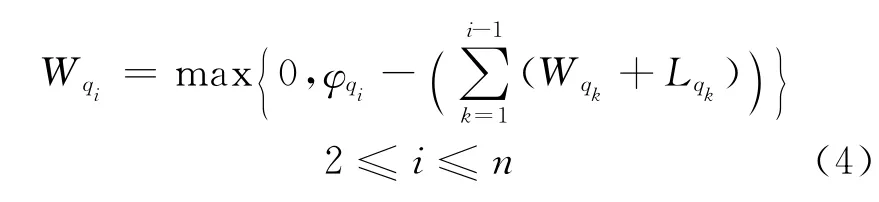
下面针对表3计算出的结果采用2种不同的取车顺序所得到的调机总等待时间.见表4、表5.

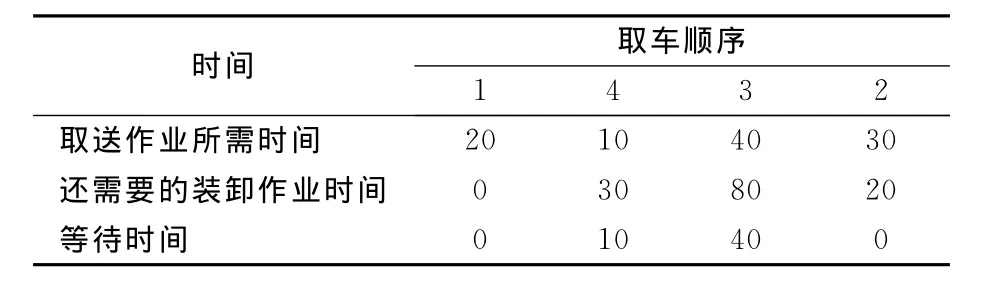
表4 取车顺序为1－4－3－2时的计算结果min

所以调机总等待时间为：0＋10＋40＋0＝50 min.

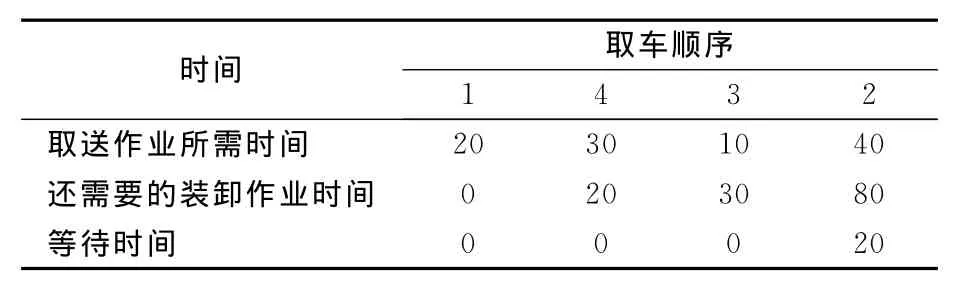
表5 取车顺序为1－2－4－3时的计算结果min

这时的调机总等待时间为：0＋0＋0＋20＝20 min.两者相比，在送车顺序一定的情况下，显然第二种取车顺序更好.

2 建立数学模型

根据对放射形专用线直达车流取送车问题的分析可知，使各专用线的调机等待时间最小的取送车方案才是最好的方案，而这由取送车顺序决定.假定某一货运站有n条专用线，用集合I＝｛1，2，…，n｝表示.送车顺序用S（s1，s2，…，sn）表示，取车顺序用Q（q1，q2，…，qn）表示.

如果在取送过程中为各地点提供的装卸作业时间都大于等于其所需时间，那么调车机车在去各地点取车时装卸作业都已完成，无需等待，这是最理想的情况.在一般情况下，由于在车辆取送过程中为某些专用线提供的装卸时间不足，就会产生调车机车到部分专用线取车之前必须等待一段时间.对取送车方案的优化是使总的等待时间最小.

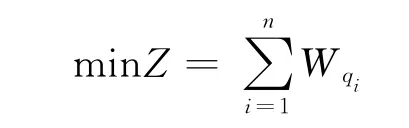
因此，放射形专用线直达车流取送车问题的数学模型可完整表示如下.

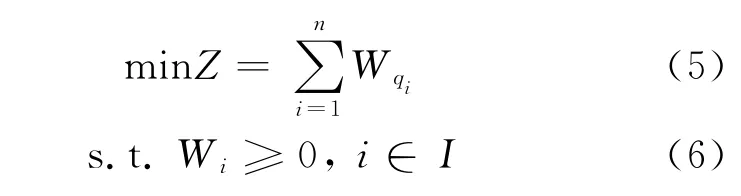
3 算法设计

根据放射形专用线直达车流取送车问题的特点，设计了一种改进的模拟退火算法，用于此问题的求解.模拟退火算法是基于Monte Carlo迭代求解策略的一种通用的随机寻优算法，最早由Metropolis等于1953年提出，1983年Kirkpatric等将其应用于组合优化问题，目前已在VLSI、生产调度、车辆路径、机器学习等诸多领域得到成功应用［9－10］.

编码方式.

对送车顺序采用顺序编码方案，简单自然.如编码为［4 2 1 3］的一个方案表示按专用线4－2－1－3的顺序送车.而送车顺序一旦确定，各专用线完成装卸的时间也就可以确定下来了.那么此时，到最先完成装卸作业的专用线取车显然是最有利的.

取车顺序由装卸完成的早晚决定，而装卸完成的早晚是由送车顺序决定的，所以，送车顺序决定取车顺序.如果没有考虑这一点，n条专用线的送车顺序有n！种，取车顺序也有n！种，取送车方案总共有n！×n！＝（n！）2种方案；考虑这一特点，问题的解空间则会从（n！）2急剧下降到n！，搜索空间大大缩小，有利于提高算法的寻优能力.因此本算法只对送车顺序进行编码，不对取车顺序进行编码.取车顺序由装卸完成的先后来确定.

邻域的构造：在采用顺序编码的模拟退火算法中（例如求解TSP问题），2点交换（SWAP）算子是最常见的邻域构造方法，此外还有反转算子（INV）和插入算子（INS）［11］.如果送车顺序是1→2→3→4→5，2个点分别是第二个点和第五个点（见图4a）），则分别采用2点交换、反转和插入算子得到的新的送车顺序见图4b）～d）.

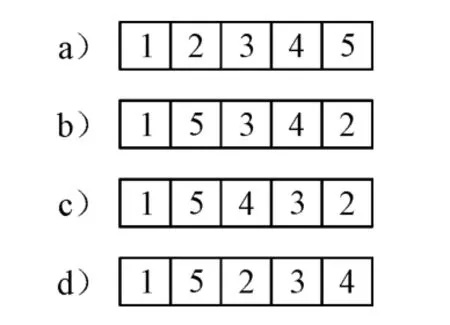
图4 顺序编码和3种算子的运算结果

为了提高算法的寻优能力，本算法将上述3种算子结合起来用于邻域构造，方法是根据概率来选用不同的算子.具体来说，如果规定在邻域构造时70%的情况下使用2点交换算子，20%的情况下使用反转算子，10%的情况下使用插入算子，也就是说这三种算子使用的概率分别是0.7，0.2和0.1.那么在实际运用时，首先产生一个［0，1）之间的随机数r，如果0.0≤r＜0.7，就使用两点交换算子，如果0.7≤r＜0.9就使用反转算子，如果0.9≤r＜1.0就使用插入算子.邻域构造方式的多样化也有利于提高算法的寻优能力.

温度控制：初始温度为T0＝100，终止温度为Tf＝0.01，每个温度下的内循环次数为100次.降温函数定义为：Tk＋1＝αTk.其中：降温系数α＝0.96.

4 仿真结果与分析

本文用CJHJ语言编写程序实现了这一算法，对应.Net Framework版本为4.0.为检测算法的性能，特地构造了如下3个算例，专用线数量分别是8条、9条和10条.针对每个算例都进行了100次仿真计算，每次计算的随机数种子各不相同，得到的最好取送车方案和调机总等待时间见表6～7.

文中编写了一个穷举法的程序，对上述3个算例的全部送车方案一一进行计算（送车方案数分别为40 320，362 880，3 628 800个），结果表明，改进的模拟退火算法找到的最好解就是该算例的最优解.见表8、图5～图6.

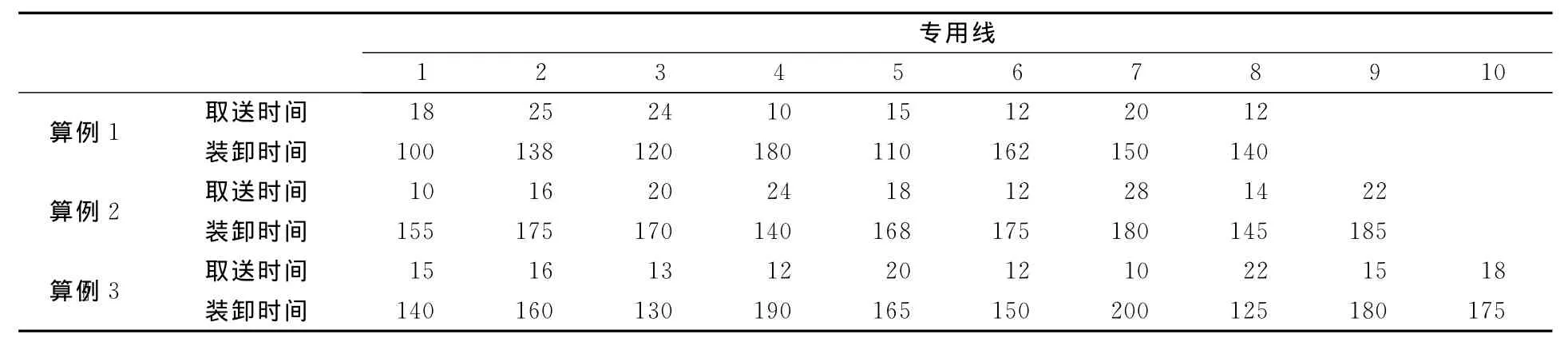
表6 3个算例的取送时间和装卸时间 min

表7 3个算例的最好取送车方案

表8 3个算例的计算时间比较

图中圆点表示在降温过程中当前方案的调机总等待时间.此图形象地表示出了模拟退火算法在一次仿真实验的迭代过程中即能向好的方向搜索，也能向差的方向搜索，温度较高时波动剧烈，温度较低时稳定性有所提高，即使有较大的偏离也能很快的回到当前最好解的附近，在局部搜索和全局搜索2个方面实现了较好的平衡.

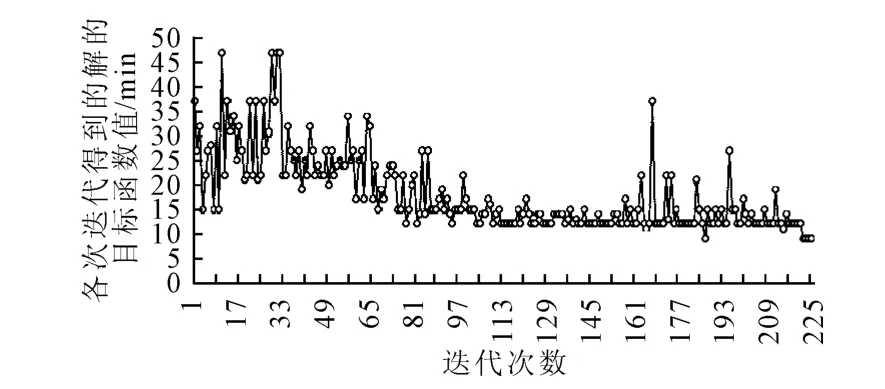
图5 算例3的1次仿真计算的完整迭代过程

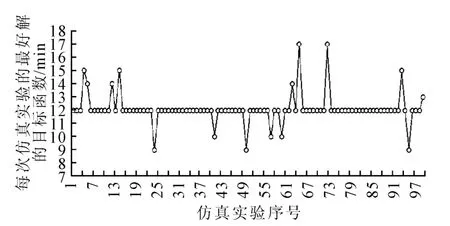
图6 算例3的100次仿真实验得到的最好方案的调机总等待时间

对算例3进行了100次实验得到的最好解的目标函数的分布见图7，即等待时间为9min的出现了3次，出现最多的是等待时间为12min的方案，共出现85次.

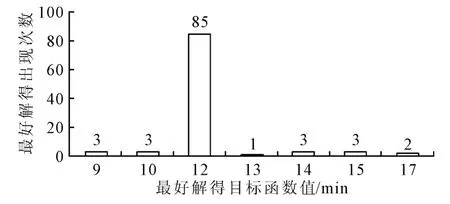
图7 算例3的100次仿真结果分布图

算法寻优能力分析.

按照所设定的温度控制参数，设温度从初始的100℃下降到0.01℃

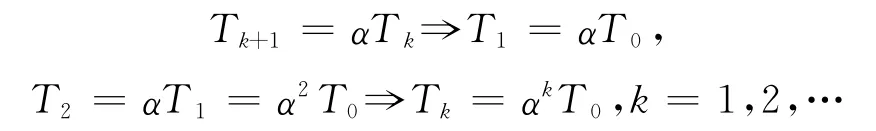
设温度从初始的100℃下降到0.01℃需要迭代n次，则

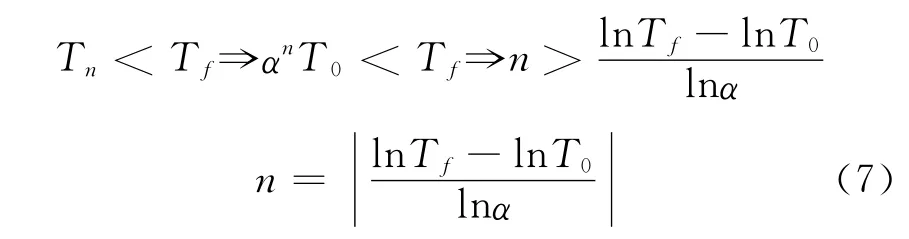
将T0＝100，Tf＝0.01和α＝0.96代入式（3）得到n＝226.

根据算例3进行分析，有10条专用线，送车顺序就有10！＝3 628 800种.整个降温过程从初始温度到最终温度共经历226个温度，在每个温度下都迭代100次，总共检查了22 600个解，只占解空间总数的0.62%，但结果已经令人非常满意，可见该算法无论是求解速度还是解的质量都是比较高的.

5 结束语

放射形专用线直达车流取送车方案的优劣直接影响到车辆周转和货物送达的时间.针对这一问题在模拟退火算法中，用顺序编码表示送车顺序，按一定概率使用两点交换、插入和反转算子来构造邻域，加快了收敛速度，提高了搜索能力，能够尽量压缩调车机车非生产等待时间，其计算性能通过仿真实验结果也得到了充分验证.这一思想不仅能够运用到树枝状专用线取送车方案的优化中，也能运用到一般组合优化问题中提高求解速度和寻优能力.

［1］彭其渊，王慈光.铁路行车组织［M］.北京：中国铁道出版社，2007.

［2］宋建业，谢金宝.铁路行车组织基础［M］.北京：中国铁道出版社，2005.

［3］宋建业.直达列车多点装卸取送顺序优化的表上移动法［J］.兰州铁道学院学报：自然科学版，2002（1）：76－79.

［4］王慈光.放射形专用线非直达车流取送车问题研究［J］.交通运输工程与信息学报，2006，4（3）：16－23.

［5］牟峰，王慈光，杨运贵.放射形专用线非直达车流取送车模型及算法［J］.铁道学报，2009，31（3）：2－5.

［6］牟峰，王慈光，左大杰，等.放射形专用线取送车模型及算法［J］.西南交通大学学报，2010，45（1）：104－110.

［7］李海军，朱昌锋.放射形铁路专用线直达车流取送车问题的单亲遗传算法研究［J］.铁道科学与工程学报，2011，8（6）：114－117.

［8］雷友诚，吴志飞.改进的蚁群算法在放射形专用线取送车优化中的应用［J］.控制工程，2012，19（6）：1007－1010.

［9］KIRKPATRIC S，GELATT C D，VECCHI M P.Optimization by simulated annealing［J］.Science，1983，220：671－680.

［10］KIRKPATRIC S，TOULOUSE G.Configuration space analysis of traveling salesman problem［J］.J Phys，1985，46：1277－1292.

［11］王凌.智能优化算法及其应用［M］.北京：清华大学出版社，2001.

［12］雷友诚，涂祖耀，桂卫兵，等.基于遗传蚁群算法的树枝型铁路取送车问题优化［J］.中南大学学报：自然科学版，2011（8）：55－58.