地铁客流分析及列车发车间隔优化研究*
2015-04-18刘兰芬杨信丰
刘兰芬 杨信丰
(兰州交通大学交通运输学院 兰州 730070)
0 引 言
地铁作为大城市公共交通的重要组成部分,对缓解城市交通拥堵,促进城市交通的可持续发展有重要作用.地铁客流在1d内随着人们的生活习惯和工作需要而变化,工作日的出行规律和休息日的出行规律也有着明显的不同.由于地铁客流具有动态性和时变性特点,就需要根据实际情况调整行车间隔时间.发车间隔的确定是地铁运营中十分重要的组成部分,对于吸引客流和提高服务水平都具有十分重要的意义.
部分学者对行车间隔时间进行了相关研究.林震等[1]对影响轨道交通发车间距的因素进行了分析,以运营者效益最大化与社会福利最大化为目标函数,建立了发车间距的优化模型.洪玲等[2]分析了不同的行车间隔对实际客流需求以及系统运输能力的影响,给出变化趋势曲线,对行车间隔进行优化调整.F.J.Vázquez-Abad等[3]建立了乘客等待时间的优化模型,使用离散仿真模型对原模型进行简化,通过计算寻求最优的服务水平.严波[4]提出了以乘客满意度和企业满意度加权平均值最大为总体目标的行车间隔时间优化模型,并在一条具体的实例线路上演示了计算和分析的过程.徐育锋等[5]根据客流在时间上变化的规律,建立以乘客的等车费用、车内费用和运营企业变动费用总和最小为目标的轨道线路行车间隔非线性优化模型.肖枫[6]以乘客为出发角度,参考城市公共交通系统,建立了一个以乘客满意度和企业满意度为优化目标的轨道交通行车间隔时间优化理论模型.刘涛等[7]提出了换乘站大客流行车间隔协调调整策略,建立了基于行车间隔协调调整的换乘站大客流处置优化模型.L.F.Liu等[8]研究了基于行车间隔城市轨道交通列车在换乘站的换乘协调问题.
由于客流的动态变化,需要根据实际情况调整行车间隔时间,以满足客流需求.鉴于此,本文综合考虑列车满载程度及乘客舒适度,建立多目标行车间隔时间优化模型;采用基于NSGA-II的多目标遗传算法求解该问题的Pareto解集,综合考虑相邻时段发车间隔的稳定性,确定各时间段的发车间隔.
1 客流分析
1.1 时间分布特性分析
1.1.1 工作日客流时间分布
地铁客流在1d内随着人们的生活习惯和工作需要而变化.图1是某工作日某地铁2号线工作日的进出站客流量分布图,从图中可知,该地铁客流在1d内形成2个客流高峰,在早高峰和晚高峰时,同时存在较高的进站和出站客流,其他工作日的客流量时间分布规律与此类似.

图1 工作日进出站客流图(周二)
由图1可见,早高峰客流量较大,进出站的早高峰客流峰度大于晚高峰客流峰度,但晚高峰的时间跨度大于早高峰,说明早高峰时段客流比较集中,晚高峰峰值相对于早高峰客流变化较缓和;另外,可以看出进站客流的早晚高峰均早于出站客流的早晚高峰.由此可知,该地铁线路客流具有通勤、通学特性.
1.1.2 周末客流时间分布
图2为周末客流分布图,可知周六与周日的客流时间分布规律有相似之处,均无明显的早晚高峰,周末客流与工作日客流时间分布存在明显的差异,周末最高峰没有工作日客流高,但周末平峰时段的客流量却大于工作日的客流量,说明周末旅客出行较分散.周六与周日的客流分布规律亦有不同之处,周六早上进出站客流均远大于周日的客流,可能是由周末加班的职工和学生造成.

图2 周末进出站客流对比图
1.1.3 “五一”客流时间分布
图3为“五一”客流分布图.由图3可见,“五一”与周末的客流时间分布规律有相似之处,均无明显的早晚高峰,但“五一”的客流量大于周末的客流量,“五一”的早上进出站客流较大.

图3 “五一”与周末进出站客流对比图
1.2 客流聚类分析
从地铁客流时间分布特性可知,每日的客流特性并不完全相同,特别是工作日与周末及节假日.为了提高地铁服务质量及降低运行成本,需要根据不同的地铁客流分布特性确定列车的开行间隔.Frey等[9]提出了近邻传播聚类算法(affinity propagation,AP算法),该方法能较快地处理大规模数据,可得到比较稳定的聚类结果.因而本文利用AP聚类算法对地铁客流数据进行聚类分析,将客流数据分为若干个子类,进而针对每一子类确定其列车开行间隔.
对于一个有N个样本的地铁客流数据集,AP算法定义任意2个样本xi,xk之间的相似度为

AP算法的基本步骤如下.
步骤1 设m=0,最大迭代次数为M,计算数据集的相似度矩阵S,设定相似度矩阵对角线元素为相同值p,设定初始可信度和可用度r(0)(i,k)=0,a(0)(i,k)=0及阻尼系数λ.
步骤2 如果m大于M ,则转步骤5,否则,m =m+1按式(2)及(3)计算r(m)(i,k),a(m)(i,k);
步骤3 按下式更新可用度和可信度.

步骤4 确定聚类中心,(r(m)(i,k)+a(m)(i,k)>0时认为是一个聚类中心),返回步骤2.
步骤5 将其余点根据相似度划分到各个聚类中,算法结束.
本文选取某地铁2号线的站点进行观测,以30min为时间间隔,对2014年4~5月客流数据进行统计.利用AP算法进行聚类分析,取参考度p为-35 000,得到的聚类数及聚类结果见表1.从聚类结果来看,周六和周日在一个聚类内,周一至周五的客流数据聚集为一类,而“五一”前1d在一个分类内,“五一”假期为单独一类.
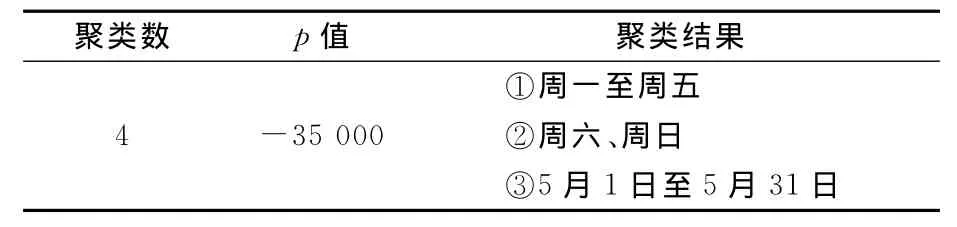
表1 客流聚类结果表
2 发车间隔优化模型的建立
2.1 模型的假设
地铁列车行驶过程受众多因素影响,模型在建立时考虑了以下假设:(1)同一时间段的发车间隔固定;(2)每一时间段内客流均匀到达和离开车站;(3)车辆选型和编组固定列车定员人数固定;(4)列车全程匀速运行,未发生安全事故;(5)同线路上各列车一次运行的运营成本相同.
2.2 符号及变量说明
K={k|k=1,2,…,N}为城市轨道交通线路断面集合,N为断面数量;Q为列车定员;q为线路的最大断面客流量;T为调度模拟时间段;h1,h2为模拟期间的最小及最大发车间隔;I为模拟期间线路发车数;m1,m2为模拟期间的最小及最大车辆满载率;d为车内乘客站立人员密度.
2.3 模型分析及建立
1)乘客舒适度 地铁车厢拥挤程度直接影响乘客的乘车舒适度,用车辆内乘客站立人员密度作为衡量舒适度的标准,也是定员标准[10].《城市轨道交通工程项目建设标准》建议的车辆内乘客站立人员密度评价标准见表2.

表2 车内乘客站立人员密度评价标准表
车内乘客站立人员密度d可表示为

式中:S为列车坐席数量;A为列车立席区分配面积.
对于乘客而言,当舒适度空间恰好接触但不挤压乘客身体,乘客可小幅活动,此时乘客的舒适度良好,随着乘客数量的增加,舒适度逐渐降低,根据表2的标准,可构建乘客舒适度的分段效用函数如下:

2)满载程度衡量 地铁运营管理者为了降低经营成本,往往会增大发车间隔,以增加列车的满载程度.满载率一般可用车内实际的乘客数与车辆定员的比值来表示,可构建以下效用函数对满载率进行衡量.

式中:α为成本参数;β为强度系数.本文取α=40,β=10.
依据上述分析,构建地铁列车行车间隔优化模型如下.

其中:式(9)为发车间隔限制约束;式(10)为车辆满载率约束.
3 求解算法
由于本模型由2个相互冲突的目标函数构成,因而需要寻求该模型的Pareto最优集.遗传算法作为一种启发式的搜索算法,在多目标优化问题中得到了广泛的应用.其中,NSGA-II(nondominated sorting genetic algorithm II)采用简洁明晰的非优超排序和排挤机制,使算法具有逼近Pareto最优前沿的能力,并采用排挤机制保证得到的Pareto最优解具有良好的散布,表现出较好的综合性能[11].本文基于 NSGA-II设计模型的求解算法.
1)染色体的构造 采用二进制编码方式表示模拟时间段内的发车数,发车数满足约束条件(9)及(10).
2)交叉算子 按交叉概率pc从父代选择一些染色体,两两分组,并对每组染色体进行如下操作:随机产生两个交换位,将两条染色体中的基因进行交换,从而得到两条新的染色体.
3)变异操作 对popsize个染色体以变异概率pm进行变异:对被选择变异染色体的基因,随机产生一个变异位置,并重新产生其基因,从而得到一条新的染色体.
4)拥挤度选择算子 快速非支配排序:设ni为种群中支配个体i的个体数,Si为种群中被个体i支配的个体集合.快速非劣分层的具体步骤为[12].
步骤1 找出种群中所有ni=0的个体,并保存在当前集合F1中.
步骤2 对于当前集合F1中每个个体i,遍历Si中每个个体l,执行nl=nl-1,如果nl=0,则将l保存在集合H 中.
步骤3 记F1中得到个体为第一个非支配层的个体,并以H为当前集合,重复以上操作,直到整个种群被分层.
确定拥挤度计算步骤为
步骤1 对同层的个体初始化距离,令每个体i的拥挤度初始值L[i]d=0.
步骤2 对不同的目标函数,重复步骤3-1~3-3操作.
步骤3-1 对同层的个体按目标m的函数值进行优劣排序;
步骤3-2 使得排序边界上的个体具有选择优势,给定一个大数L[0]d=L[l]d=∞ ,以确保进入下一代;
经过快速非支配排序和拥挤度计算,群体中的每个个体i都得到两个属性:非支配序irank和拥挤度id.进而可采用轮盘制选择算子进行选择,具体过程为:对于个体i,j,当irank<jrank或irank=jrank且id>jd时,选择i,如果2个个体在同一级,取周围较不拥挤的个体.
4 算例分析
选取某地铁2号线为例,以30min为时间间隔,对2014年4~5月客流数据进行统计.利用AP算法进行聚类分析,结果见表1,对应时段的最大客流断面见表3.该线路列车采用6辆编组,定员Q为1 440人,列车坐席数量S为240,列车立席区分配面积A为200m2,最大发车间隔为10 min,最小发车间隔2min,最大车辆满载率为1.1,最小车辆满载率为0.7.利用本文设计的模型及算法对4类客流进行行车间隔优化.
计算结果见表3.综合考虑相邻时段发车间隔的稳定性,确定4类客流列车开行的间隔见表4.从优化结果来看,该线路各时段乘客的舒适度均较好,在07:00~22:00间满载率也较高,说明本文设计的模型及算法具有较好的适用性.
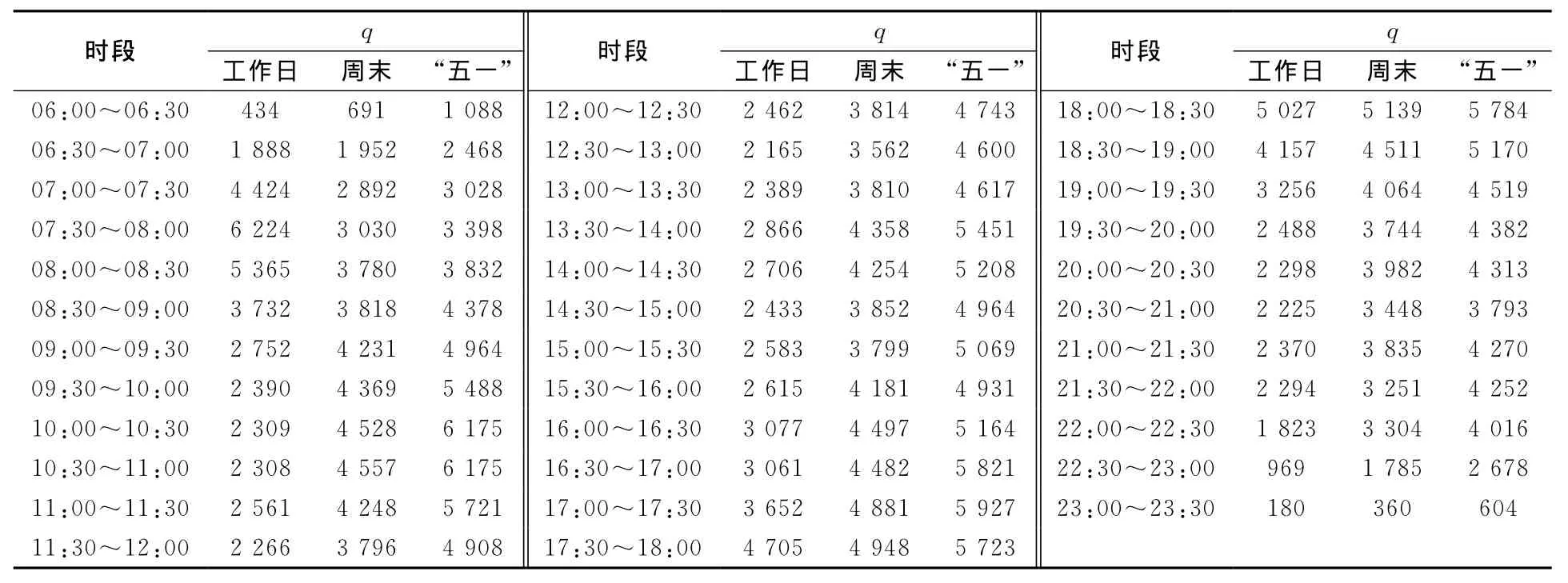
表3 4类客流优化结果min

表4 4类客流列车开行间隔结果min
5 结束语
本文综合考虑列车满载程度及乘客舒适度,建立多目标行车间隔时间优化模型;采用基于NSGA-II的多目标遗传算法求解该问题的Pareto解集,该解集可为运营管理者提供多个可选择方案;最后,综合考虑相邻时段的发车间隔的稳定性,确定了各时间段的发车间隔.算例分析表明本模型在地铁列车行车间隔调度方面是合理可行的,但本模型没有考虑地铁线路间的乘客换乘影响,需要在今后进一步深入研究.
[1]林 震,杨 浩.城市轨道交通发车间距优化模型探讨[J].土木工程学报,2003,36(1):1-5.
[2]洪 玲,陈菁菁,徐瑞华.市域快速轨道交通线行车间隔优化问题研究[J].城市轨道交通研究,2006,9(3):35-37.
[3]VáZQUEZ-ABAD F J,ZUBIETA L.Ghost simulation model for the optimization of an urban subway system[J].Discrete Event Dynamic Systems,2005,15(3):207-235.
[4]严 波.城市轨道交通行车间隔时间优化模型研究[J].城市轨道交通研究,2008,11(6):53-57.
[5]徐育锋,范炳全,何胜学,等.单轨道交通线路行车间隔优化模型研究[J].交通与运输,2010,26(12):104-107.
[6]肖 枫.基于模糊神经网络的城市轨道交通行车间隔时间优化研究[D].重庆:重庆交通大学,2013.
[7]刘 涛,徐瑞华.基于行车间隔协调调整的换乘站大客流处置[J].城市轨道交通研究,2014,17(2):50-53.
[8]LIU L F,YANG X F,YANG K.Research on the multi-objective transfer coordination optimization of urban rail transit trains[J].Journal of Information &Computational Science,2015,12(5):1855-1864.
[9]FREY B J,DUECK D.Clustering by passing messages between data points[J].Science,2007,315(5814):972-976.
[10]中华人民共和国建设部.建标104-2008城市轨道交通工程项目建设标准[S].北京:标准出版社,2008.
[11]王 林,陈 璨.一种基于DE算法和NSGA-II的多目标混合进化算法[J].运筹与管理,2010(6):58-64.
[12]KALYANMOY D,AMRIT P,SAMEER A,et al.A fast elitist multi-objective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
