基于灰色系统理论田庄煤矿工业广场建筑物变形数据分析

侯曰鹏

（山东能源临沂矿业集团田庄煤矿，山东 济宁272100）

0 引言

近年来，随着科学技术的迅猛发展和我国现代化进程的不断加快，各类高耸建筑物雨后春笋般拔地而起。由于建筑物增高、荷载增加，在地基基础和上部结构的共同作用下，建筑物会产生不同程度的沉降，其中有些不均匀沉降轻者会使建筑物产生倾斜或出现裂缝，影响正常使用，重者将危及建筑物的安全。为了保证建筑物施工和运营的安全，避免造成经济损失和人员伤亡，建筑物的变形预测已成为建筑工程防灾减灾的一个重要方面，所以需要定期对高层建筑和重要建筑进行沉降观测，获得沉降变形数据，并对其进行预测分析，掌握建筑物沉降变形的规律，正确预测变形大小，以便及时采取适当的预防或善后措施，确保建筑物的安全使用。

本文提出灰色系统理论在建筑物沉降预测方面的应用，并以田庄煤矿工业广场建筑物沉降变形为例，分别利用传统GM（1，1）模型和改进后模型，建立等间隔灰色预测模型对其沉降数据进行分析。

1 灰色系统理论简介

灰色系统理论是我国学者邓聚龙教授于20世纪80年代提出的。它是以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，主要通过对部分信息的生成、开发，提取有价值的信息，实现对系统运行行为和演化规律的正确把握和描述。

灰色系统理论与方法的核心是灰色动态模型，特点是生成函数和灰色微分方程。灰色动态模型是以灰色生成函数概念为基础，以微分拟合为核心的建模方法，灰色系统建模思想是直接将时间序列转化为微分方程，从而建立抽象系统的发展变化动态模型，即Grey Dynamic Model，简记为GM。灰色数列预测是指利用动态GM模型，对系统的时间序列进行数量大小的预测，即对系统的主行为特征量或某项指标，发展变化到未来特定时刻出现的数值进行预测。

1.1 灰色预测模型建模的思想

原始序列(非负序列)经过一次累加生成后，形成一个单调递增数列，新序列中各数据点的连线可以用指数函数（y=aebx）进行拟合。根据这个指数函数可以推导出下一个(即第一个预测期)累加值的预测值，最后通过累减生成将累加序列预测值还原为原始序列预测值。

1.2 传统GM（1,1）模型

设非负原始序列:

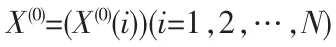
对X(0)作一次累加，则：

求出相应的 1-AGO 序列：X(1)={X(1)(k)}(k=1，2，…，N)；

Z(1)为X(1)的紧邻均值生成序列：

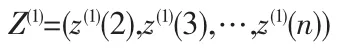
其中：

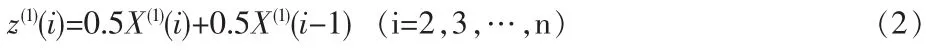
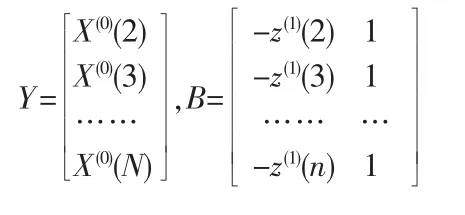
则微分方程系数向量：

得微分方程动态模型及时间响应函数：

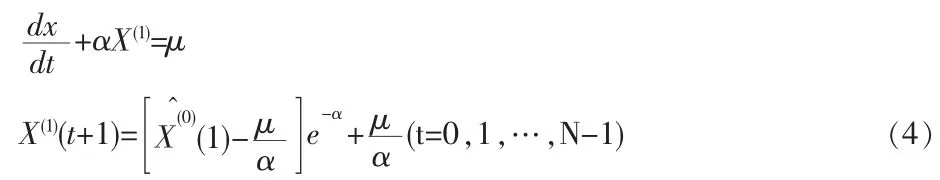
由上式求出生成数的回代计算值X(1)(i)，然后计算原始数据的还原值：

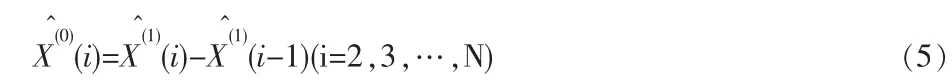
1.3 改进后GM(1，1)模型

设非负原始数据列为：

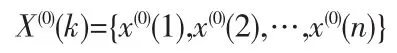
对X(0)(k)作一次累加生成(1-AGO)，得生成数列：

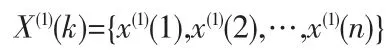
其中：

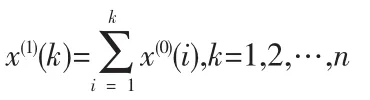
则对生成数列X(1)(k)有如下白化微分方程：

若将上式在区间[k，k+1]上积分，有：

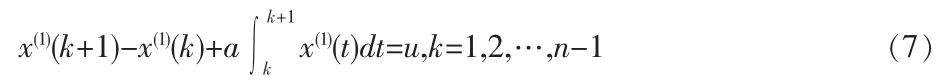
当设Z(1)(k+1)为x(1)(t)在区间[k，k+1]上的背景值时，则有：

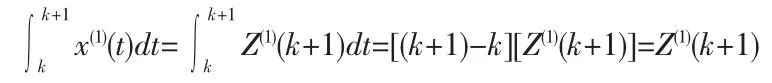
由此可知这里的背景值即为x(1)(t)在区间[k，k+1]上的定积分。

由于方程（6）的解为指数形式，为方便起见，x(1)(t)可以用如下指数曲线近似表示：

并假设该曲线过x(1)(k+1)和x(1)(k)两点，因此有

由上式可得：

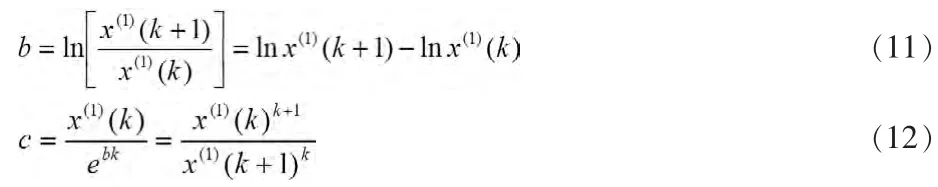
因此背景值为：

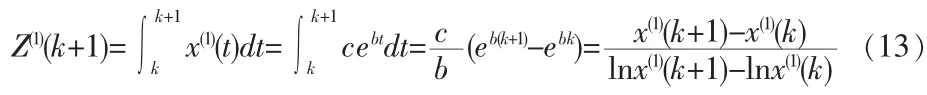
注意到：

因此上式可表示为：

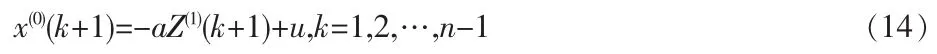
将上式用矩阵表示，则：

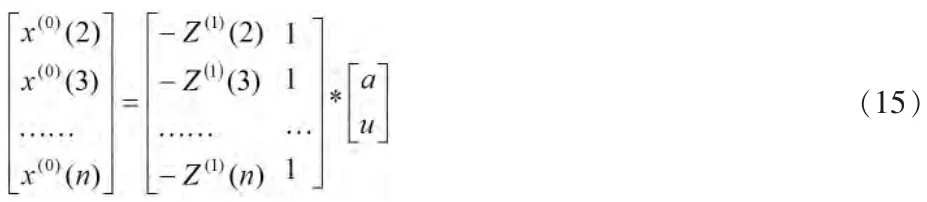
令

由式（17）求出背景值B后，然后按传统模型的计算方法算出经累减还原后即可得到的估计值。

1.4 精度检验

对模型精度的评定方法有残差大小检验、关联度检验和后检差检验三种，灰色模型的精度通常用后验差方法检验。

设由 GM（1，1）模型得到：

记原始数列X(0)及残差数列∈的方差分别为S21，S22，则有：

后验差比值：

C=S2/S1

指标C是后验差检验的重要指标，指标C越小越好，C越小，表示S1越大而S2越小。S1大表示原始数据方差大，原始数据离散程度大，S2小表明残差方差小，残差离散程度小，C小就表明尽管原始数据很离散，而模型所得计算值与实际值之差并不太离散

平均精度检验：

很据残差： ∈(0)(i)=X(0)(i)-(0)(i)(i=1，2，…，N)

模型相对误差为:

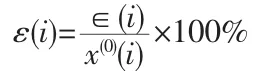
2 工程应用

2.1 工程概况

拟建工程位于济宁市高新区王因镇，所在区域属于煤矿塌陷区。建筑物主楼为地上6层，框架结构，基础埋深约7.4m；基坑东西长约93m，宽约71m，拟开挖6.5米。按本工程支护设计方案，本基坑东侧北段及南侧西段设计安全等级为一级，余位二级。

2.2 基准点、工作基点、沉降观测点的布设

2.2.1 基准点、工作基点的布设

根据现场情况及设计要求，在工地附近及路上距测区较远且坚实稳固的位置，布设四个水准基点 BM1、BM2、BM3、BM4。基准点使用钢筋标志，采用深埋方法设置。高程采用任意高程基准。

2.2.2 沉降观测点的布设

根据建筑物的结构特点，在楼室外主要承重柱及基础能反映建筑物地基变形的位置一共布设了26个沉降观测点，沉降观测点采用一体式螺栓观测标志。

2.3 数据处理

本文以L1沉降观测点的15期数据进行处理分析，分别基于传统GM（1,1）模型和改进后GM（1,1）模型对数据进行了处理，并作了相关比较。

综合上述两种模型算法数据，得到两种模型数据对比，如表1；建立实测模拟预测数据对比，如图1所示。分别如下：

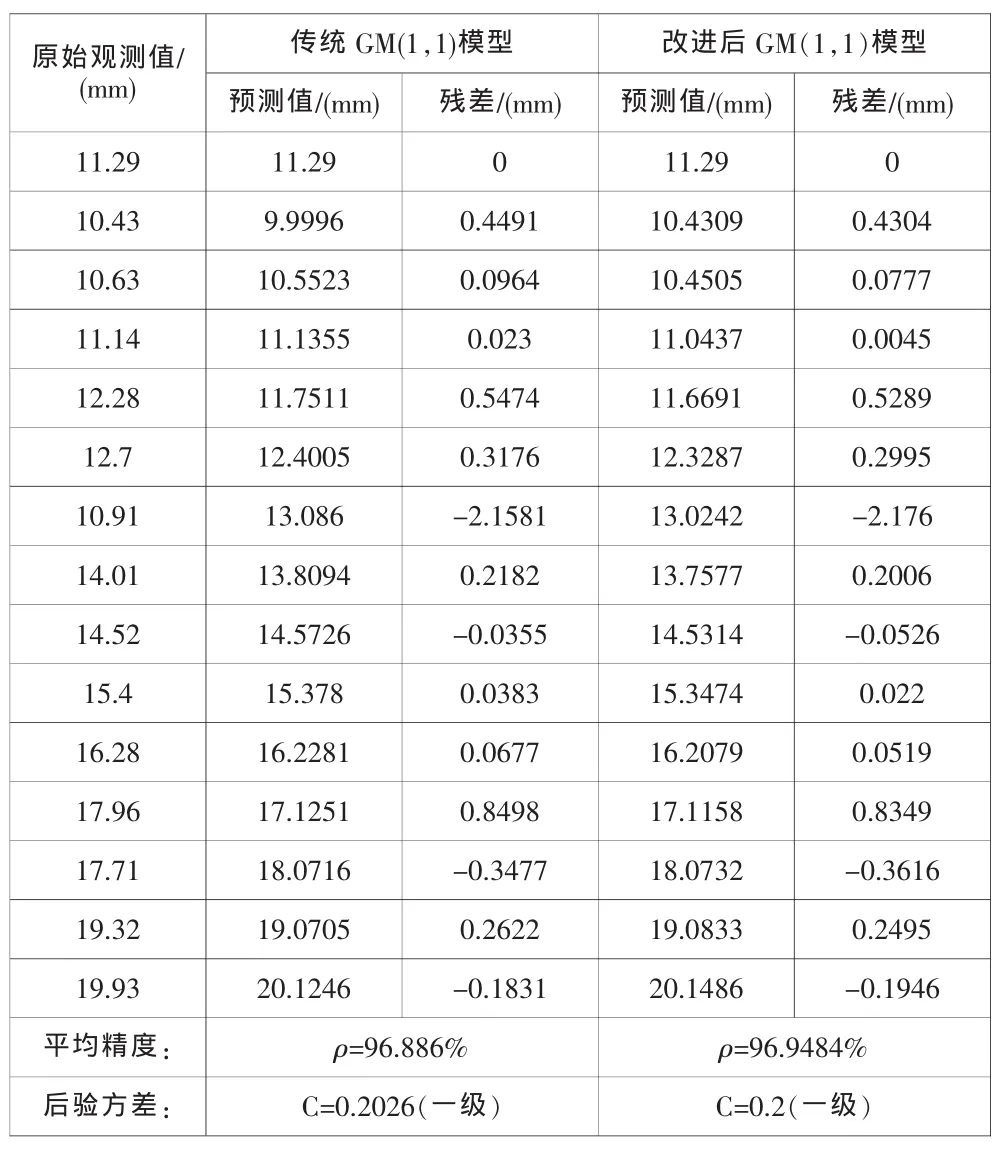
表1 L1点数据对比

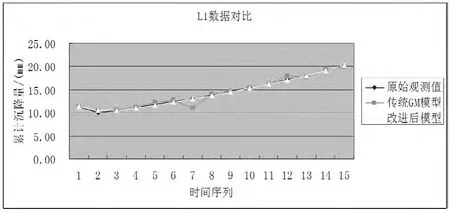
图1 L1数据对比示意图

3 结论

传统GM(1，1)模型得到的短期模拟数据精度较高，背景值计算方法简单，计算量小，但是随着预测时间的延长，其模拟预测的结果精度逐渐降低。同时，其模拟预测曲线在变化趋势上总体出一条单调曲线，其变化率逐渐减小，曲线走向趋于缓和，在某种程度上不能很好映变形数据的反复性与复杂性。是做短期预测的较优模型。

改进后GM(1，1)模型不仅适用于低增长序列、也适用于高增长序列；不仅适用于短期预测，同样也适用于中、长期预测。预测、拟合精度相近，误差可修正。因此GM(1，1)改进模型是一种比较好的拟合和预测模型。

［1］陈鲤江,等.数学表达式的归一化方法研究[J].浙江工业大学学报,2012(02).

［2］王永,等.利用Excel绘制误差椭圆的方法[J].矿山测量,2008,12.

［3］李水兵,李培现.基于BP神经网络的深基坑变形预测[J].测绘信息与工程,2011,10(06).

［4］王永,等.基于分形的线要素综合数据处理方法[J].矿山测量,2009,10.

［5］苗元欣.基于一元线性回归的变形监测数据处理与分析[J].山西建筑,2013(33).