基于双相介质理论的储层参数反演方法

桂金咏， 高建虎， 雍学善， 李胜军

1 中国石油勘探开发研究院西北分院, 兰州 730020 2 中国石油天然气集团公司油藏描述重点实验室, 兰州 730020



基于双相介质理论的储层参数反演方法

桂金咏1,2， 高建虎1， 雍学善1， 李胜军1

1 中国石油勘探开发研究院西北分院, 兰州 730020 2 中国石油天然气集团公司油藏描述重点实验室, 兰州 730020

传统基于单相介质理论的储层参数反演方法将孔隙流体与固体骨架等效为单一固体，弱化了孔隙流体的影响，反演结果精度不高. 本文提出根据双相介质理论反演储层参数的方法. 首先，在前人研究的基础上，利用岩石物理模型建立弹性参数与孔隙度、饱和度、泥质含量等储层参数间的关系，进而将双相介质反射系数推导为储层参数的函数；其次，根据贝叶斯反演理论，在高斯噪声假设的基础上，采用更加符合实际情况的修正柯西分布函数描述反射系数的稀疏性，推导出储层物性参数目标反演函数；最后, 应用差分进化非线性全局寻优算法来求解目标反演函数，使得反演结果与实际资料间误差最小. 新方法旨在突出流体对介质反射系数的影响，以期得到较高的储层参数反演精度. 模型与实际资料测试均表明该方法可行、有效且反演精度较高.

双相介质； 储层参数； 反演； 岩石物理模型； 贝叶斯框架

1 引言

地震波特征分析，尤其是地震波振幅随偏移距变化(AVO)分析，在储层预测中有着非常重要的地位. 不同储层以及同一种储层的孔隙流体特征不同时，对地震振幅的影响规律也不同. 储层内部性质如孔隙发育程度、孔隙流体类型、流体饱和度的改变会对地震振幅造成一定的影响(Hilterman, 1989，2001；Russell et al., 2003). 反映储层内部性质的储层参数，如孔隙度、泥质含量、饱和度等参数是预测油气分布、估算油气储量、确定开发井位的重要参数.

传统的储层参数获取方法将含流体储层等效为单一固体，利用地震波反射振幅随偏移距变化特征开展叠前AVO反演，其理论基础是Zoeppritz方程(Avseth et al.，2005; Grana and Della Rossa, 2010). Zoeppritz方程是描述地震振幅在两种单相固体介质分界面处的反射与透射规律的基本方程 (Zoeppritz, 1919). 然而，含油气储层并非完全固体的弹性介质. 通常情况下，含油气储层为孔隙、裂缝型，表现为固体骨架与流体双相介质特征. 由于流体的存在以及固体与流体的相互作用会弱化岩石的力学性质，弹性波在双相介质中的传播比在单相介质中的传播更具复杂性，双相介质中不仅有第一类纵波，还有第二类纵波，地震波的反射与透射机理与单相介质存在着较大的差别(Biot, 1956, 1962； 雍学善等，2006). 因此，传统基于单相介质理论的Zoeppritz方程难以准确描述地震波在双相介质中的传播过程和规律.

Biot理论的提出奠定了双相介质传播理论的基础. 双相介质理论充分考虑了介质的岩石骨架结构和孔隙流体性质以及局部特性与整体效应的关系，将含流体储层表述为固体相和流体相的复合体，且分别考虑了固体和流体以及二者相互耦合对地震波传播的影响(Biot, 1956, 1962).Geertsma和Smit(1961)研究了饱和流体孔隙介质分界面上纵波垂直入射时的反射透射问题. Nur和Wang(1989, 1999)总结了早期学者关于双相介质的理论、模型与实验的研究成果，较为详细地论述了流体饱和度、裂隙密度、孔隙度、孔隙流体压力与围压、裂隙与孔隙空间几何形态等因素对地震波传播的影响以及孔隙性岩石地震波的传播特点，并指出了双相介质理论在测井评价、强化回收率、断层检测、油气区域圈定等领域的应用前景. 王尚旭(1990)研究了双相介质中地震波的传播规律，实现了双相介质中地震波传播的有限元解法，并对单相和双相介质反射系数进行了比较，指出当双相介质孔隙度较大且孔隙流体的弹性模量和密度与固体颗粒相同量级时，两者有明显差异. Wu等(1990)和乔文孝等(1992)对弹性波在双相介质分界面处任意入射角下的反射、透射特征进行了研究. 牟永光(1996)通过数值模拟实验，观测到了双相介质中慢速纵波和慢速横波的存在并给出了双相介质AVO方程的具体表达式. 杨顶辉(2002)从微观流场的流体相对流动各向异性速度和Biot宏观流体的双相各向异性介质中弹性波方程出发，实现了双相各向异性介质中“相对流体位移”的有限元波场模拟. 雍学善等(2006)，高建虎等(2007)对双相介质AVO方程进行了参数简化及反演研究，为双相介质地震波传播理论的实际应用开辟了新的途径. 王华青和田家勇(2011)从岩土力学、地球物理勘探、声学研究等领域方面总结了双相介质弹性波传播问题在理论、动态参数的测量技术、动力响应分析方面的研究成果.这些成果的获得为我们进一步研究双相介质储层参数反演提供了坚实的基础.

本文直接从双相介质地震波反射理论出发，将双相介质反射系数简化为储层参数的函数，并建立了新的目标反演函数及非线性求解算法.通过模型反射系数敏感性分析、目标函数收敛性分析以及实际资料测试，表明了方法的可行性与有效性.

2 方法原理

2.1 双相介质反射系数方程

在两个半无限的双相介质分界面处，平面纵波Pi以入射角αi入射到分界面，将产生以下几类波：第一类反射纵波P11，第二类反射纵波P12，反射横波S1，第一类透射纵波P21，第二类透射纵波P22，透射横波S2，如图1所示.

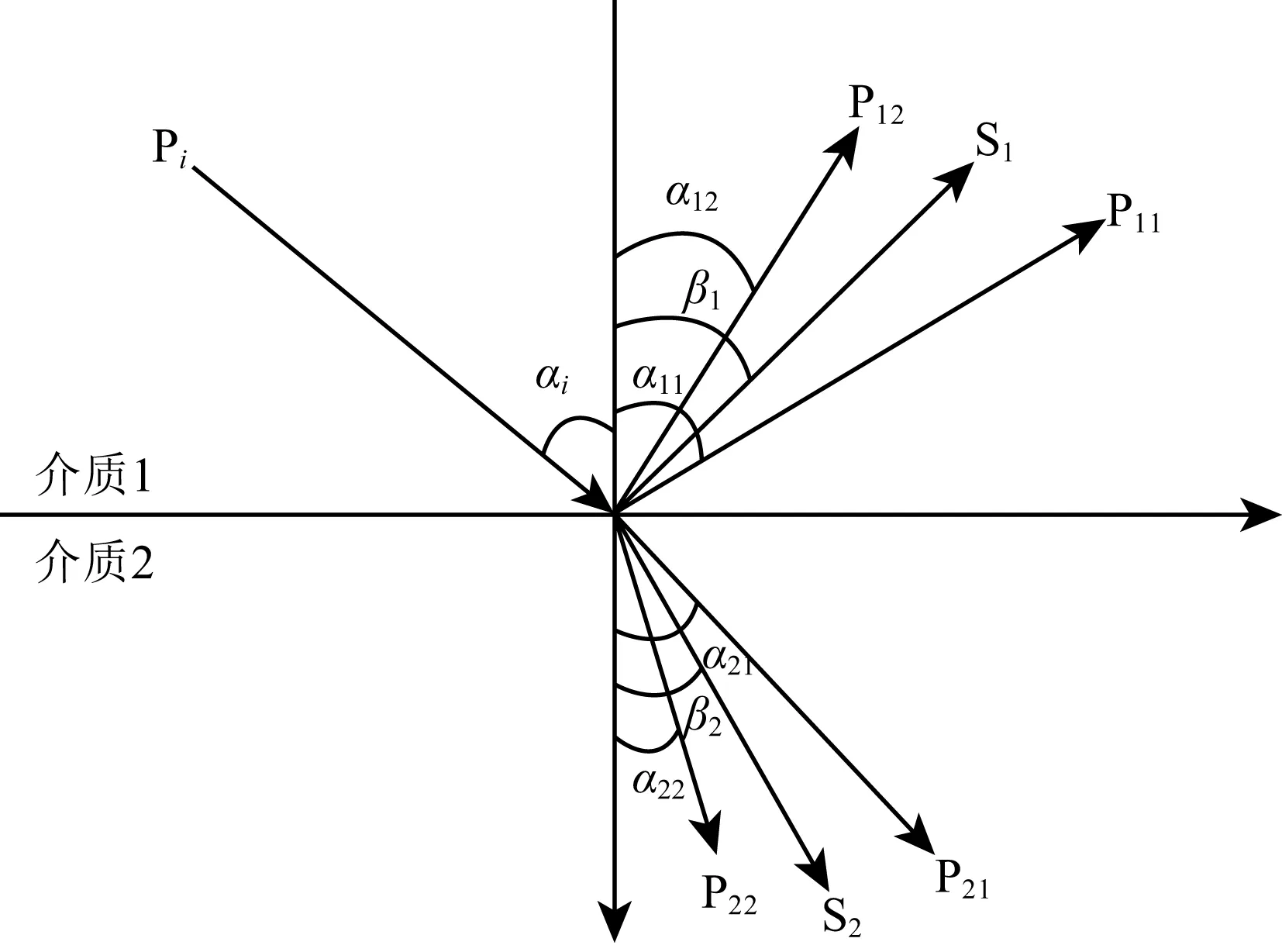
图1 两种介质分界面上的反射与透射Fig.1 Reflection and transmission on the surface of the boundary between two media

定义快纵波反射系数RP11=AP11/APi，慢纵波反射系数RP12=AP12/APi，横波反射系数RS1=AS1/APi，快纵波透射系数TP21=AP21/APi，慢纵波透射系数TP22=AP22/APi，横波透射系数TS2=AS2/APi. 在平面波传播斯奈尔定律以及固体法向、切向位移连续、法向总应力连续、固体切向应力连续、流体压力及流体法向流量连续等六个边界条件的假设基础上，根据牟永光(1996)的推导结果，有：

(1)

由方程(1)可以看到，双相介质反射系数和透射系数方程并不像Zoeppritz方程那样简单，用纵波速度、横波速度和密度等3个弹性参数就可以表达，而需用10多个参数才能表达. 其中，包括4个双相介质弹性参数(A、N、Q、R)、3个质量参数(ρ11、ρ22、ρ12)、2个流体与固体振幅比参数(m1、m2)以及孔隙度(φ). 如此多的参数很难由地震资料反演求取且与常用的描述储层内部性质的含气饱和度、孔隙度等储层参数差异较大，在实际工作中很难使用. 需要进一步推导，将双相介质反射系数方程改写为储层参数的函数.

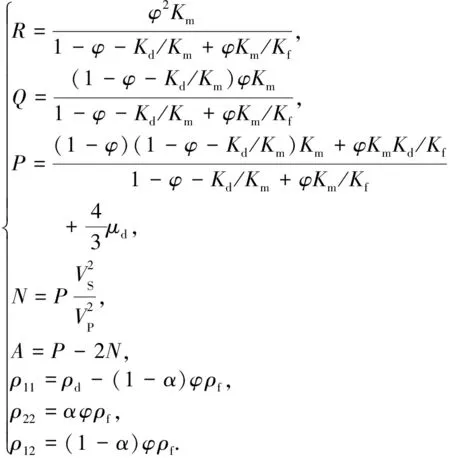
(2)

其中Km、Kd、Kf分别为基质、干岩、混合流体的体积模量；μd为干岩剪切模量；ρd、ρf分别为干岩、流体的体积密度；α为曲折度，可以利用Berryman关系式α=1-r(1-1/φ)求取，r介于0和1之间(Berryman et al.，1995).

重点在于未知弹性参数Km、Kd、Kf、μd、ρd、ρf的求取. 岩石物理模型是建立弹性参数与储层参数间定量关系的桥梁. 以砂岩天然气储层为例，通过多种岩石物理模型可将弹性参数E描述为含气饱和度Sg、孔隙度φ以及泥质含量Vsh的函数：E=f(Sg,φ,Vsh).因此，可根据实际研究区地层岩石物理特点选择合适的岩石物理模型将双相介质参数进一步转化为储层参数的函数.

在砂岩天然气储层中，饱和岩石一般由粘土、石英、水、气等成分组成. 记Kc、Ks、Kw、Kg分别表示粘土、石英、水、气的体积模量，μc、μs分别表示粘土、石英的剪切模量；ρc、ρs、ρw、ρg分别表示粘土、石英、水、气的体积密度. 一般采用Voight-Ruess-Hill平均求取岩石基质模量(Mavko et al., 2009)：

(3)

不同岩石物理模型对岩石孔隙结构的描述不同，主要体现在对干岩模量的求取方式上，具有代表性的有Krief模型、Nur模型、Pride模型以及Hertz-Mindlin模型等(Nur et al.,1998; Mavko et al., 2009). 对于一般干燥岩石，可根据Nur的临界孔隙度理论，利用临界孔隙度φc将孔隙介质的机械和声波特征分成两个截然不同的区域，大于临界孔隙度为悬浮域，小于临界孔隙度为承载域，可以得到在承载域下的干岩体积、剪切、密度模量(Nuretal.,1998)：

(4)

多种流体共存的混合模式主要有均匀分布和斑块饱和分布(White, 1975). 在天然气储层中一般倾向于斑块饱和分布(MavkoandMukerji，1998). 通过合理调节斑块参数e可以得到流体体积模量Kf与含气饱和度间的关系(Brie et al., 1995)：

Kf=(Kw-Kg)(1-Sg)e+Kg.

(5)

由Wood公式建立含气饱和度Sg同流体密度ρf的关系(Mavko et al., 2009)：

ρf=Sgρg+(1-Sg)ρw.

(6)

最后，根据Gassmann理论，可以得到饱和岩石弹性参数与储层参数间关系(Mavkoetal., 2009)：

(7)

式(3)—(6)中饱和岩石组分模量参数一般通过岩石物理实验或经验统计得到. 表1给出了本文采用的饱和岩石组分模量参数. 在通过(3)—(7)式获得饱和岩石弹性参数后，代入(2)式得到双相介质参数. 最后可由雍学善等(2006)的方法得到流体与固体振幅比参数(m1、m2).

表1 饱和岩石组分模量参数Table 1 Modulus value of saturated rock components

至此，通过合理的岩石物理模型假设，可以将双相介质参数转化为储层参数的函数，进而代入(1)式，双相介质反射系数方程便可以转化为饱和度Sg、孔隙度φ以及泥质含量Vsh的函数.双相介质反射系数方程简化为三个未知参数的函数，较原反射系数方程未知参数大大减小，更加有利于叠前AVO反演. 通过改写后的双相介质反射系数方程，反射系数与饱和度、孔隙度及泥质含量等储层参数间建立起了直接的关系，使得双相介质储层参数的反演成为可能. 然而，这种关系为高度非线性关系，需要进一步建立一套非线性反演机制才能从地震振幅中得到准确的储层参数.

2.2 目标反演函数

基于贝叶斯反演理论框架，构建目标反演函数. 按照地震褶积模型：

d=Gr+n,

(8)

其中d=[d1,d2,…,dN]T是观测得到的地震数据，r=[r1,r2,…,rM]T是反射系数序列，G是N×M维子波矩阵，n=[n1,n2,…,nN]T表示观测噪声.由贝叶斯公式可得以下近似式：

P(r|d)∝P(r)·P(d|r),

(9)

其中：P(r|d)表示反射系数的后验概率密度信息，P(r)表示反射系数先验概率密度信息，P(d|r)表示似然函数.

一般地面地震观测数据的噪声服从零均值、协方差矩阵为CS的高斯分布(Downton, 2005).当给定反射系数r之后，则观测数据与模型参数之间的似然函数P(d|r)可以通过该观测方式下噪声的分布特征来表示，即P(d|r)=

(10)

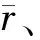
(11)

根据贝叶斯反演框架，后验概率分布P(r|d)表达了从观察数据中获得的对未知量的认知程度：

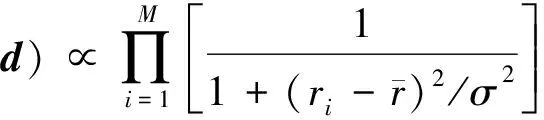
(12)

由贝叶斯理论可知，使(12)式取最大值的解为反射系数的最优解，即对模型参数的最大后验概率密度解.

对(12)式两边同时取对数，整理后即可得到目标反演函数：

(13)

若任给一组饱和度、孔隙度、泥质含量参数，即(Sg,φ,Vsh)i，就可以得到一条与之相应的反射系数曲线ri. 因此，反演问题就变成了通过选择合适的一组参数(Sg,φ,Vsh)i，使得目标函数J(ri)为最小的过程.

2.3 非线性反演

考虑到求解精度与效率，本文采用差分进化(Differential Evolution，DE)算法对目标反演函数(13)式进行非线性求解. 同遗传算法一样，DE算法也是基于群体智能理论的优化算法，通过群体内个体间的合作与竞争产生的群体智能指导优化搜索. 但与传统遗传算法相比，其采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性且易于并行实现，效率较高且不需要借助问题的特征信息，适于求解一些利用常规的数学规划方法所无法求解的复杂优化问题(Storn and Price, 1997).

设初始种群规模是由N个D维参数向量表示的个体xi=[xi,1,xi,2,…,xi,D]组成，则该种群通过变异、交叉、选择等三个过程即可得到下一代种群 (StornandPrice, 1997; 印兴耀等，2013)：

(1)变异操作

(2)交叉过程

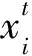
其中，RAN(j)∈[0,1]代表均匀分布随机数；C为交叉概率常数；RANn(i)∈[1,2,…,D].

(3)选择标准

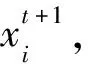
3 可行性分析

3.1 反射系数敏感性分析

叠前地震资料振幅随偏移距的变化实质是反射系数随入射角的变化. 不同储层参数值对应的反射系数值差异越明显，表示反射系数对储层参数的敏感性越强，利用反射系数反演该储层参数的可能性也就越大. 设斑块饱和参数e为3，依据表1中岩石物理参数和临界孔隙度为0.4的Nur岩石物理模型以及(1)—(7)式(如无特别说明，文中分析实例的岩石物理模型及参数均同此)，建立一个两层泥、砂岩模型用来分析在不同入射角情况下含气饱和度、孔隙度、泥质含量的变化对双相介质反射系数的影响. 模型储层参数及变化范围如表2所示. 固定孔隙度、泥质含量及含气饱和度三参数中的两个，另一参数在某一范围内变化，相应的反射系数随入射角变化情况如图2所示.

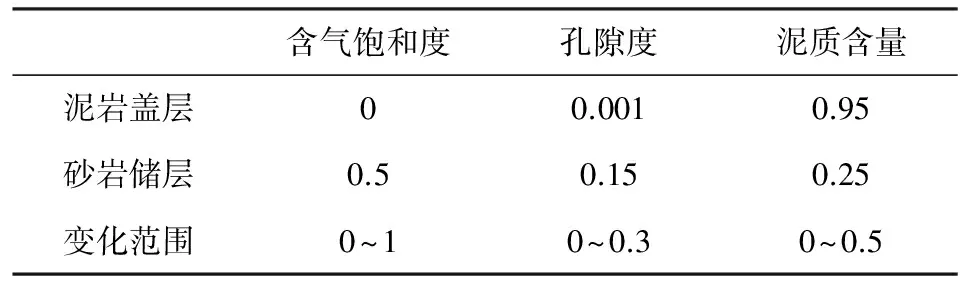
表2 敏感性分析模型参数Table 2 Model parameters for sensitivity analysis

由图2可以看到，含气饱和度、孔隙度及泥质含量的改变都会对反射系数的变化造成一定的影响且影响程度与入射角有关.

在泥质含量与孔隙度固定的情况下，可以发现随着含气饱和度的增加，反射系数间的差异逐渐减小，这种趋势随着入射角的增大越发明显. 在入射角小于35°的范围内，不同含气饱和度值对应的反射系数值差异较大，易于区分.当入射角大于35°时，随着入射角的增大，高含气饱和度值对应的反射系数值差异越来越小.

在含气饱和度与孔隙度固定的情况下，模型的泥质含量设定在砂岩岩性范围内0～0.5. 可以发现低泥质含量(小于0.3)对应的反射系数值在入射角小于35°的情况下，差异明显.入射角大于35°时，差异逐渐变小，直至重合.而高泥质含量(大于0.3)对应的反射系数值在入射角临近50°时，仍有明显的差异.

在含气饱和度与泥质含量固定的情况下，可以发现不同孔隙度对应的反射系数值差异较含气饱和度、泥质含量尤为明显，且在50°后仍有一定差异.

整体上在泥岩、砂岩分界面处，双相介质反射系数对含气饱和度、泥质含量、孔隙度变化的敏感程度依次增强. 当入射角大于临界角时，反射系数会发生剧烈变化，对储层参数的敏感性变得十分复杂.

图2 反射系数随储层参数及入射角的变化(色标表示反射系数值)，(a)、(b)、(c)分别为反射系数随含气饱和度、泥质含量、孔隙度及入射角的变化Fig.2 Reflection coefficient versus reservoir parameters and incident angles (the color codes represent the reflection coefficient values): (a) reflection coefficient versus gas saturation and incident angles, (b) reflection coefficient versus shale content and incident angles, (c) reflection coefficient versus porosity and incident angles

图3 目标函数收敛情况Fig.3 The convergence of objective inversion function

实际地震资料的入射角范围一般小于35°，在临界角以内. 因此，在实际应用中，利用振幅随入射角的变化特征来反演储层参数是可行的.

3.2 目标函数收敛性分析

通过反射系数敏感性分析可以确认利用振幅随入射角的变化反演储层参数是可行的，但反演目标函数的收敛性关系到能否具备全局最优解. 建立一个两层砂泥岩模型，通过给定砂岩储层参数取值范围-50%～50%，设定入射角度为0°～40°，利用目标反演函数(13)式分析双相介质反演目标函数能否收敛到极小值，模型参数如表3所示.

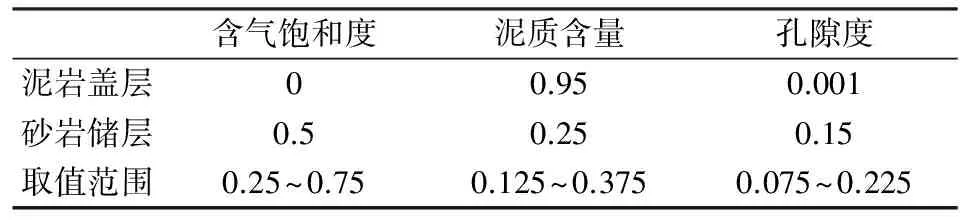
表3 收敛性分析模型参数Table 3 Model parameter for convergence analysis

由图3a—3c可以看到，目标函数收敛域形态呈椭球状，椭球的短轴方向较长轴方向易收敛. 整体上看，目标函数对含气饱和度、泥质含量、孔隙度的收敛程度虽有所差别，但均能收敛到极小值附近.

固定含气饱和度，分析孔隙度、泥质含量取值与目标函数的关系，由图3a可以看到，目标函数沿纵向变化快，沿横向变化慢，说明砂岩储层中孔隙度较泥质含量易收敛.

固定泥质含量，分析孔隙度、含气饱和度与目标函数的关系，由图3b可以看到，目标函数沿纵向变化快，沿横向变化慢，说明砂岩储层中孔隙度较含气饱和度易收敛.

固定孔隙度，分析泥质含量、含气饱和度与目标函数的关系，由图3c可以看到，目标函数沿横向变化快，沿纵向变化慢，说明砂岩储层中泥质含量较含气饱和度易收敛.

通过反射系数敏感性分析以及目标函数收敛性分析，可以得出这样的结论：在实际叠前地震资料入射角范围内，反射系数整体上对孔隙度、泥质含量、含气饱和度的变化较为敏感且目标函数能收敛到极小值，利用叠前地震资料反演储层参数是可行的且能得到最优解.

4 方法测试

4.1 模型测试

依据表1中岩石物理参数和临界孔隙度为0.4的Nur岩石物理模型，利用A区测井曲线计算得到的双相介质反射系数与40 Hz零相位雷克子波褶积，合成角度范围为0°～35°的叠前地震角度道集(每道间隔5°)，如图4所示. 以此为基础数据对不同初始模型、信噪比条件下的模型数据进行反演结果分析.

反演过程中，DE算法的缩放控制参数F设定为0.8，交叉概率C设定为0.4，迭代次数设定为200次. 以长度为10个样点的小时窗对测井曲线进行平滑作为初始模型，反演结果如图5所示. 可见，初始模型与测井曲线十分接近，反演结果亦与测井记录非常吻合. 以长度为50个样点的大时窗对测井曲线进行平滑作为初始模型，反演结果如图6所示. 图6可见初始模型虽与测井曲线差异较大，但仍能得到较高精度的储层参数反演结果. 这得益于DE算法对初始模型的依赖程度较弱，能有效避免陷入局部极值的优点(印兴耀等，2013).

在实际地球物理勘探中，受采集环境及仪器影响，采集到的叠前地震数据不可避免的含有一定程度的噪声. 为了使模型分析结果更具实际指导意义，在合成地震记录中加入随机噪声，得到信噪比分别为10、5的含噪地震记录来分析噪声对本文方法的影响. 含噪合成地震记录如图7所示.

采用与图6相同的初始模型，利用图7中所示含噪合成地震角度道集反演孔隙度、泥质含量及含气饱和度，反演结果如图8、图9所示.

通过对比图6、图8、图9可以看到，当加入噪声时，孔隙度、泥质含量及含气饱和度反演结果在整体上均受到一定的影响，信噪比越低，影响越大. 同时也注意到，即使信噪比为5，反演结果虽有所偏离，但整体趋势仍然接近实际曲线，主要原因在于目标反演函数在构建的过程中考虑了噪声的影响. 含气饱和度受噪声影响相对于孔隙度、泥质含量稍大，其他两个储层参数在反演过程中对噪声具有一定的压制，因为通过前面的分析可以知道双相介质反射系数本身对含气饱和度的敏感性相对于孔隙度、泥质含量较低. 因此，为确保含气饱和度反演结果更加可靠，反演前需对叠前道集进行相应的叠前去噪处理.

4.2 实际资料测试

为了进一步说明双相介质储层参数反演方法的实用性，以实际测井、井旁道叠前地震道集进行反演效果测试. 在进行反演前，叠前道集已经过去噪、保幅等处理，信噪比较高. 该测试数据孔隙度、泥质含量、含气饱和度测井曲线以及叠前道集如图10所示，在630 ms左右处发育一套砂岩气藏.

图4 测井曲线及合成地震记录Fig.4 The well log curves and synthetic seismic record

选用恰当的岩石物理模型能保障储层参数转化到反射系数的正确性.利用图10中孔隙度、泥质含量、含气饱和度曲线，分别根据Nur与Krief的岩石物理模型计算弹性参数曲线，与实测弹性参数曲线对比结果如图11所示. 两种岩石物理模型的主要差异在于对干岩体积模量与剪切模量的计算方式不同，进而导致纵、横波速度的计算结果不同. 由图11可见，两种岩石物理模型计算的纵、横波速度差异较大，而密度相同，整体上Nur的岩石物理模型建模结果与实测曲线对应较好.

高信噪比的叠前地震资料以及恰当的岩石物理模型，说明该区域适合进行双相介质储层参数反演，储层参数反演结果如图12所示.

由图12可以看到，储层参数反演结果与实测结果吻合较好，630 ms处的气层特征得到了较好的反映：高孔隙、低泥质含量、高含气饱和度.

将反演过程中的地震子波与由反演成果曲线计算得到的双相介质反射系数进行褶积运算，得到合成角度道集，分析合成角度道集与实际道集的吻合程度，如图13所示.由图13可以看到，利用反演结果合成得到的角度道集与实际地震角度道集在整体上对应较好，振幅趋势一致，残差较小. 这说明反演结果是准确、可靠的.

受计算效率及成本的限制，非线性反演方法目前仍停留在二维实际资料应用阶段. 一般而言，商业气藏与贫气藏在地震资料上具有相似的反射特征，如“亮点”等，一般方法较难区分(Avseth et al., 2005). 然而，地震解释工作者仍可以根据含气饱和度的高低来确定气藏是否具有商业价值. 因此，准确的含气饱和度参数显得尤为重要. 图14为含气饱和度二维反演剖面，可以看到含气饱和度反演剖面上的高值部分与实际含气位置(红色椭圆位置)对应较好. 根据该反演剖面，地震解释工作者不仅可以确定含气储层的分布，还可以根据含气饱和度值的高低判断该储层是否具有商业价值.

5 结论

图5 小时窗平滑初始模型储层参数反演结果黑色虚线、蓝色实线、红色实线分别代表初始模型、测井数据、反演结果曲线(下同).Fig.5 Inversion results of reservoir parameters with initial model of small time window Black dash line represents the initial model curve, blue line represents the actual value, red line represents the inverted value (the same below).

图6 大时窗平滑初始模型储层参数反演结果Fig.6 Inversion results of reservoir parameters with initial model of big time window

图7 含噪合成地震角度道集(a) 信噪比为10； (b) 信噪比为5.Fig.7 Synthetic seismic record with noise in the angle domain(a) Signal-noise ratio is 10; (b) Signal-noise ratio is 5.

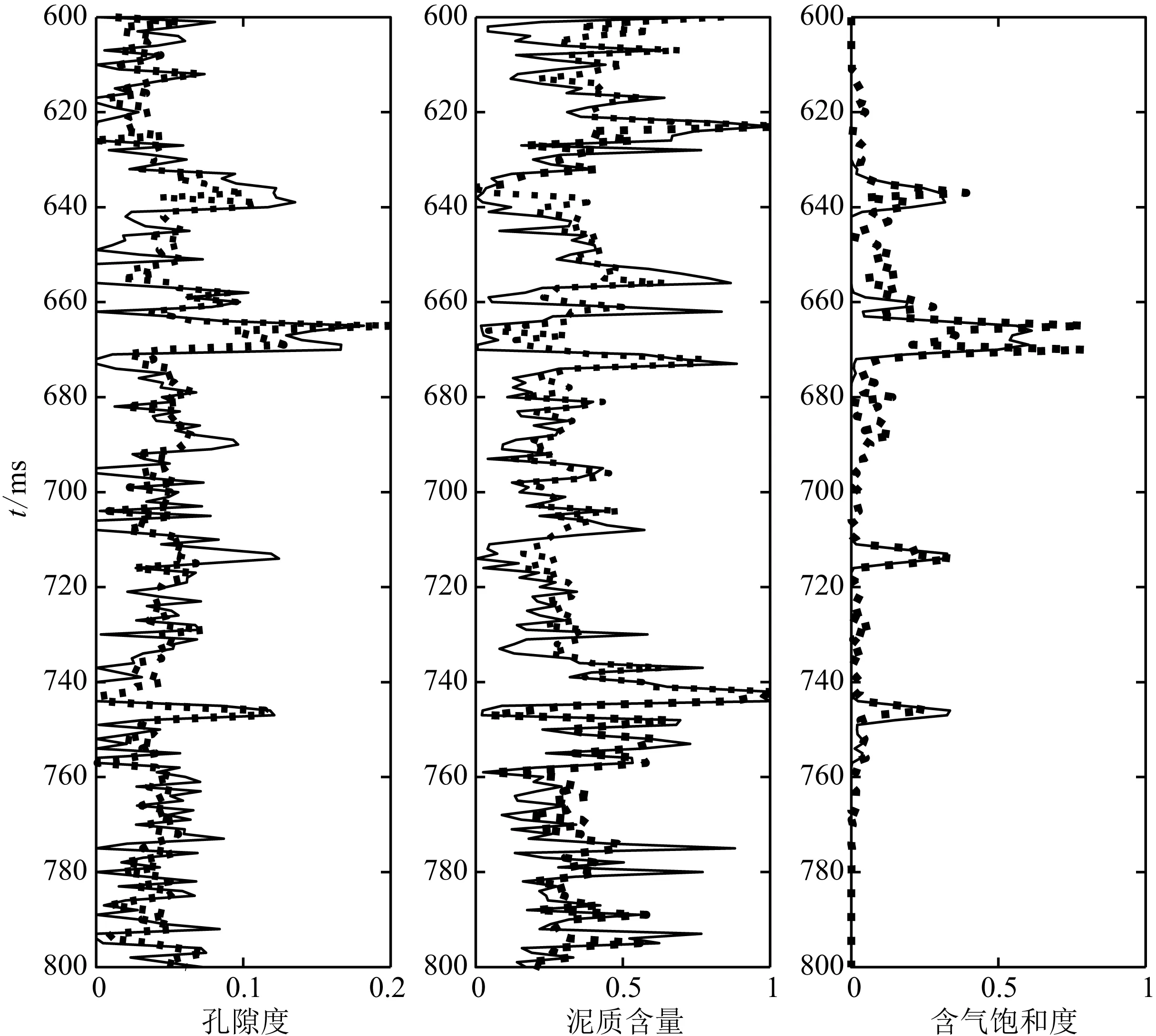
图8 地震数据信噪比为10时的储层参数反演结果实线、虚线分别为实际测井、反演曲线(下同).Fig.8 Inversion results of reservoir parameters with signal-noise ratio is 10 Solid line represents the actual value, dash line represents the inverted value (the same below).

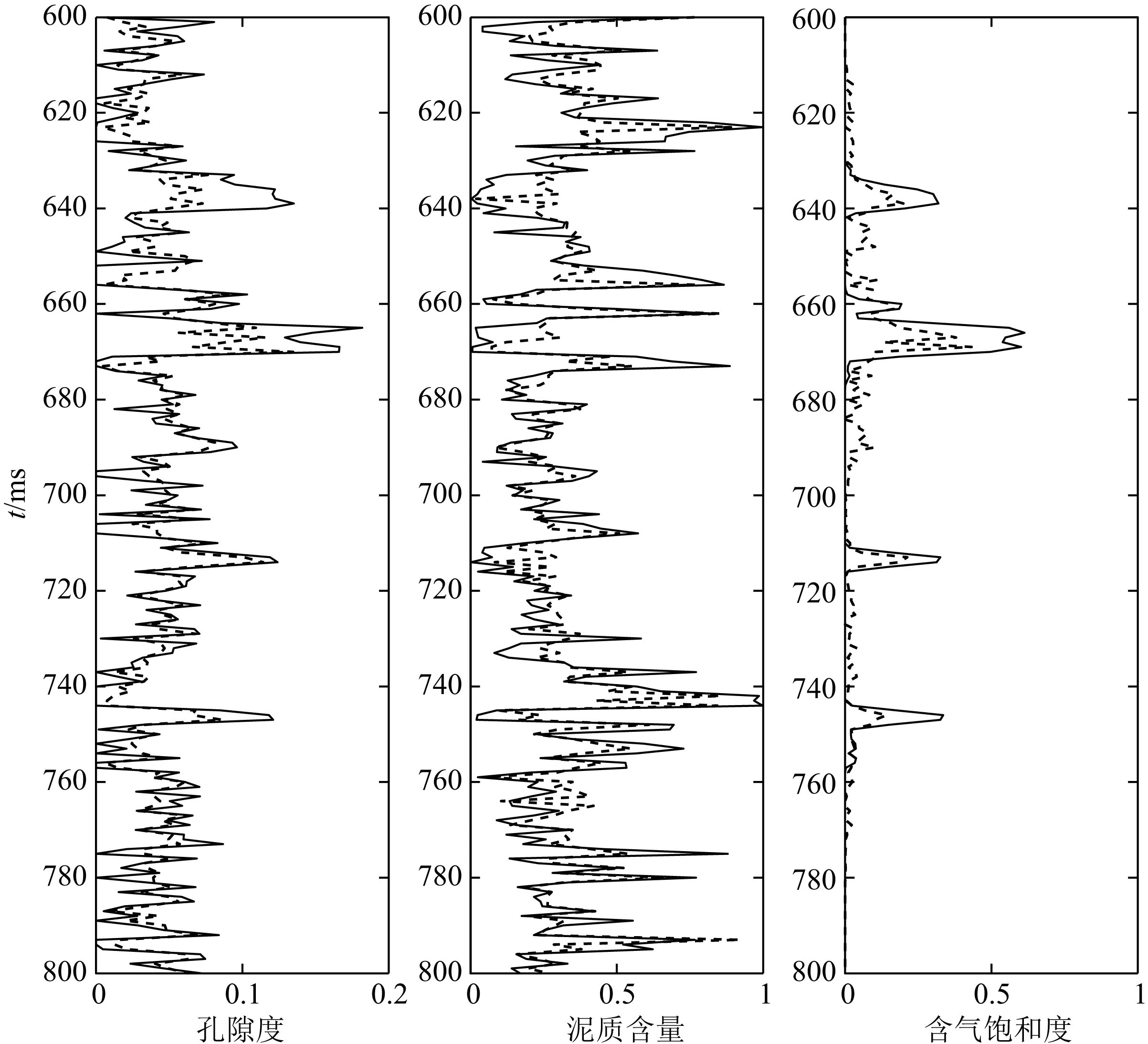
图9 地震数据信噪比为5时的储层参数反演结果Fig.9 Inversion results of reservoir parameters with signal-noise ratio is 5

图10 实际资料储层参数测井曲线及井旁道道集Fig.10 Actual reservoir parameters well log curves and the borehole-side seismic gathers

图11 岩石物理模型弹性参数曲线黑色、红色、蓝色线分别表示实际测井曲线、Nur模型计算曲线、Krief模型计算曲线.Fig.11 Elastic parameter curves calculated by rock physical model Black line，red line and blue line respectively represent the actual curve, curve calculated by Nur′s model and curve calculated by Krief′s model.

储层参数能较好地表征储层的物性特征，评价储层的开发潜力. 当岩石含有流体时，表现为双相介质特征，常规基于单相介质理论的储层参数反演方法弱化了流体的影响，预测油气存在不足. 本文提出的储层参数反演方法，直接基于双相介质理论，突出流体的影响，利用双相介质振幅随偏移距变化规律反演储层参数. 与常规方法相比，该方法更加贴合储层实际情况. 模型与实际资料测试结果均表明，该方法具有较好的反演效果. 在实际应用过程中有几个方面需要特别注意：

(1) 本文方法受岩石物理模型的影响因素较大，不恰当的建模结果会导致储层参数与地震振幅间的联系发生严重偏离. 岩石物理实验以及大量的岩石物理模型统计分析能有效地保证建模结果的准确性；

(2) 同常规叠前地震反演方法相同，高信噪比以及保幅的叠前地震道集能保证反演结果的精度；

(3) DE算法虽然对初始模型的依赖较弱，但仍建议利用常规方法的反演结果作为初始模型，能够减少反演迭代次数，节省计算时间；

(4) 目标函数的求解具有高度非线性，涉及大量、反复的正演过程，计算量较大，高性能计算设备的投入以及高效的正、反演算法的发展能够有力推动双相介质理论走向大规模三维实际应用.

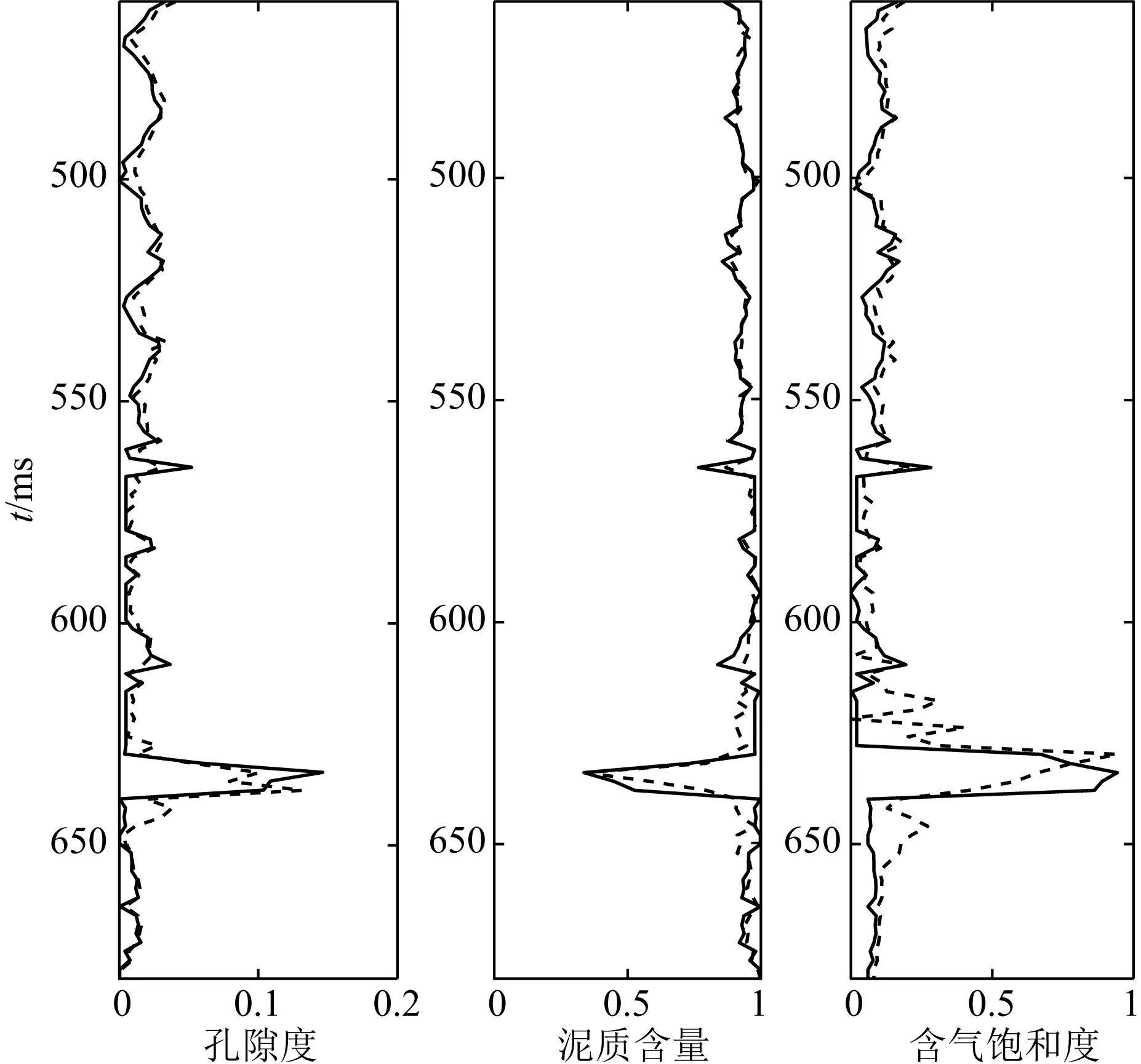
图12 储层参数反演结果实线、虚线分别为实际测井、反演曲线.Fig.12 Inversion results of reservoir parameters Solid line represents the actual value, dash line represents the inverted value.

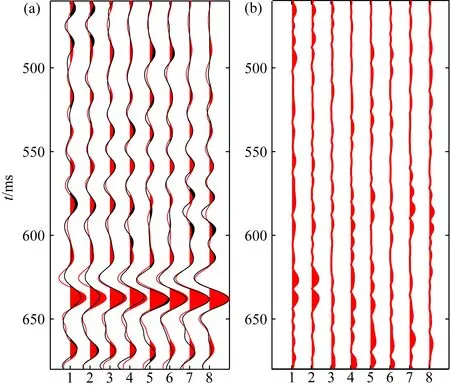
图13 反演结果合成记录与实际地震记录对比(a) 黑色、红色曲线分别为实际地震道、合成地震道; (b) 为合成地震道与实际地震道间的残差.Fig.13 The comparison between synthetic seismic and actual seismic record(a) Black curve and red curve respectively represent for the actual seismic and synthetic seismic record; (b) The errors between synthetic seismic and actual seismic record.

图14 含气饱和度反演剖面Fig.14 The inverted gas saturation profile

Avseth P, Mukerji T, Mavko G. 2005. Quantitative Seismic Interpretation: Applying Rock Physics Tools to Reduce Interpretation Risk. Cambridge: Cambridge University Press.

Berryman J G, Wang H F. 1995. The elastic coefficients of double-porosity models for fluid transport in jointed rock.JournalofGeophysicalResearchSolidEarth, 100(B12): 24611-24627.

Biot M A. 1956. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. low-frequency range.J.Acoust.Soc.Am., 28(2): 168-178.Biot M A. 1962. Mechanics of deformation and acoustic propagation in porous media.JournalofAppliedPhysics, 33(4): 1482-1498.

Brie A, Pampuri F, Marsala A F, et al. 1995. Shear sonic interpretation in gas-bearing sands. ∥SPE Annual Technical Conference & Exhibition. Dallas, Texas: SPE, 701-710.

Downton J E. 2005. Seismic parameter estimation from AVO inversion [Ph. D. thesis]. Calgary: University of Calgary.

Gao J H, Liu Q X, Yong X S, et al. 2007. The method study of pre-stack reservoir parameter inversion in dual phase media.AdvancesinEarthScience(in Chinese), 22(10): 1048-1054.

Geertsma J, Smit D C. 1961. Some aspects of elastic wave propagation in fluid-saturated porous solids.Geophysics, 26(2): 169-181.

Grana D, Della R E. 2010. Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion.Geophysics, 75(3): O21-O37.

Hilterman F J. 1989. Is AVO the seismic signature of rock properties. ∥ 59th Annual Meeting, SEG, Expanded Abstracts. Dallas, Texas, 59.Hilterman F J. 2001. Seismic amplitude interpretation: 2001 distinguished instructor short course (No.4). Houston: Geophysical Development Corporation.Mavko G, Mukerji T. 1998. Bounds on low-frequency seismic velocities in partially saturated rocks.Geophysics, 63(3): 918-924. Mavko G, Mukerji T, Dvorkin J. 2009. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media. Cambridge: Cambridge University Press. Mou Y G. 1996. Reservoir Geophysics (in Chinese). Beijing: Petroleum Industry Press.Nur A M, Wang Z J. 1989. Seismic and acoustic velocities in reservoir rocks: experimental studies. Geophysics reprint series. Society of Exploration Geophysicists.Nur A M, Mavko G, Dvorkin J, et al. 1998. Critical porosity: A key to relating physical properties to porosity in rocks.TheLeadingEdge, 17(3): 357-362.

Nur A M, Wang Z J. 1999. Seismic and Acoustic Velocities in Reservoir Rocks: Recent Developments (Vol.3). Soc of Exploration Geophysicists.Qiao W X, Wang Y, Yan Z P. 1992. Reflection and transmission of acoustic wave at a porous solid/porous solid interface.ChineseJ.Geophys. (ActaGeophysicaSinica) (in Chinese), 35(2): 242-248.

Russell B H, Hedlin K, Hilterman F J, et al. 2003. Fluid-property discrimination with AVO: A Biot-Gassmann perspective.Geophysics, 68(1): 29-39.Storn R, Price K. 1997. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces.JournalofGlobalOptimization, 11(4): 341-359.

Wang S X. 1990. Finite element numerical solution and AVO problem of elastic wave in two phase media [Ph. D. thesis] (in Chinese). Beijing: University of Petroleum.

Wang H Q, Tian J Y. 2011. Review of the investigation of elastic-wave propagation in a fluid-saturated porous solid. ∥ Bulletin of the Institute of Crustal Dynamics (in Chinese). Beijing: Seismological Press: 28-34.

White J E. 1975. Computed seismic speeds and attenuation in rocks with partial gas saturation.Geophysics, 40(2): 224-232.

Wu K, Xue Q, Adler L.1990. Reflection and transmission of elastic waves from a fluid-saturated porous solid boundary.JournaloftheAcousticalSocietyofAmerica, 87:2349-2358.

Yang D H. 2002. Finite element method of the elastic wave equation and wave-field simulation in two-phase anisotropic media.ChineseJ.Geophys. (in Chinese), 45(4): 575-583.

Yin X Y, Kong X X, Zhang F C, et al. 2013. Pre-stack AVO inversion based on the differential evolution algorithm.OilGeophysicalProspecting(in Chinese), 48(4): 591-596.

Yong X S, Ma H Z, Gao J H. 2006. A study of AVO equation in dual-phase medium and parameter simplification.AdvancesinEarthScience(in Chinese), 21(3): 242-249.

Youzwishen C F. 2001. Non-linear sparse and blocky constraints for seismic inverse problems [Ph. D. thesis]. Alberta: University of Alberta.

Zoeppritz K. 1919. On the reflection and penetration of seismic waves through unstable layers.GöttingerNachr, 1(7B): 66-84.

附中文参考文献

高建虎, 刘全新, 雍学善等. 2007. 双相介质叠前储层参数反演方法研究. 地球科学进展, 22(10): 1048-1054.

牟永光. 1996. 储层地球物理学. 北京: 石油工业出版社.

乔文孝, 王宇, 严炽培. 1992. 声波在两种多孔介质界面上的反射和透射. 地球物理学报, 35(2): 242-248.

王尚旭. 1990. 双相介质中弹性波问题有限元数值解和AVO问题[博士论文]. 北京: 石油大学.

王华青, 田家勇. 2011. 流体饱和多孔介质中弹性波传播问题的研究进展. ∥ 地壳构造与地壳应力文集. 北京: 地震出版社, 28-34.杨顶辉. 2002. 双相各向异性介质中弹性波方程的有限元解法及波场模拟. 地球物理学报, 45(4): 575-583.

印兴耀, 孔栓栓, 张繁昌等. 2013. 基于差分进化算法的叠前AVO反演. 石油地球物理勘探, 48(4): 591-596.

雍学善, 马海珍, 高建虎. 2006. 双相介质AVO方程及参数简化研究. 地球科学进展, 21(3): 242-249.

(本文编辑 何燕)

Inversion of reservoir parameters based on dual-phase media theory

GUI Jin-Yong1,2, GAO Jian-Hu1, YONG Xue-Shan1, LI Sheng-Jun1

1PetroChinaResearchInstituteofPetroleumExploration&Development-NorthWest,Lanzhou730020,China2CNPCReservoirDescriptionKeyLaboratory,Lanzhou730020,China

Traditional inversion methods of reservoir parameters based on the one-phase media theory regard the medium a single solid-phase body of solid skeleton and pore fluid, which may weaken the effect of pore fluid and lead to a lower credibility in inversion results. To make full use of fluid information in seismic amplitude and improve the precision of reservoir parameter prediction, this paper suggests a new method to invert reservoir parameters based on dual-phase media theory.Firstly, on the basis of previous work, a rock physics model is used to establish the relationship between the elastic parameter and reservoir parameter. Then a new dual-phase reflection coefficient equation is derived, which is the function of reservoir parameters. Secondly, according to Bayesian inversion theory and the Gaussian noise assumption, the modified Cauchy distribution is employed to describe the sparsity of reflection coefficients and deduce the final objective inversion function. Finally the differential evolution (DE) nonlinear global optimization algorithm is adopted to solve the objective inversion function and minimize the error between the inversion results and real data.From the reflection coefficient sensitivity analysis, the sensitivities to the reflection coefficient caused by change values of gas saturation, shale content and porosity are different. While fixing the values of shale content and porosity, we found that with the increase of gas saturation, the difference between reflection coefficient decreases. This trend is more obvious with the increasing incident angle. While fixing the values of gas saturation and porosity, the variation of reflection coefficients with low shale content values (less than 0.3) and under the condition of the incident angle less than 35° are obvious. With fixed values of shale content and gas saturation, the difference of reflection coefficients changing with porosity is more obvious than gas saturation and shale content, and there are still some difference even after 50°. From the objective function convergence analysis, the shape of convergence domain likes an ellipsoid. The porosity is easiest to converge to minimum and the shale content comes second. The convergence rate changes with reservoir parameters, but they all can converge to minimum. According to the analysis of the model, the DE algorithm used to solve the objective function is not sensitive to the initial model and is immune to noise to a certain degree. Even the initial model has great deviation and the signal-noise ratio is 5, our method still has a satisfactory result. We think that reservoir parameters are sensitive to the reflection coefficient and objective function can converge to a minimum in the range of actual incident angle. Using the dual-phase media theory to conduct reservoir parameter inversion is feasible and can achieve the optimal solution.Reservoir parameters can be quantitatively described as the reservoir characteristics. Results show that the inversion method based on dual-phase media theory can highlight the influence of fluid-phase and the method is feasible, effective and accurate. To get better actual application results, there are some problems need to be noted: (1) Inappropriate modeling results can cause a serious deviation to the relationship between reservoir parameters and seismic amplitude. Rock-physics experiments and statistical analysis can effectively ensure the accuracy of the modeling results. (2) High signal to noise ratio and amplitude-preserved seismic data can guarantee the accuracy of the inversion results. (3) The DE algorithm has weak dependence on the initial model, while using inversion results from traditional methods as the initial model can reduce iteration times and computing consumption of the DE algorithm. (4) High-performance computation equipment and high efficiency of forward and inversion algorithms can vigorously promote the application of the dual-phase media theory to large-scale 3D issues.

Dual-phase media； Reservoir parameter； Inversion； Rock physics model； Bayesian framework

桂金咏， 高建虎， 雍学善等. 2015. 基于双相介质理论的储层参数反演方法.地球物理学报，58(9):3424-3438,

10.6038/cjg20150934.

Gui J Y, Gao J H, Yong X S, et al. 2015. Inversion of reservoir parameters based on dual-phase media theory.ChineseJ.Geophys. (in Chinese),58(9):3424-3438,doi:10.6038/cjg20150934.

10.6038/cjg20150934

P631

2014-10-29，2015-06-16收修定稿

国家科技重大专项课题(2011ZX05007-006,2011ZX05019-008)联合资助.

桂金咏，男，1986年生，硕士，工程师，主要从事叠前地震反演及储层预测等方面的研究工作.E-mail:guijy@petrochina.com.cn