Two-stage DOA estimation method for passive radar based on sparse representation①
2015-04-17LiuNanSongWenlong
Liu Nan (刘 楠), Song Wenlong
(College of Mechanical and Electronic Engineering, Northeast Forestry University, Harbin 150040, P.R.China)
Two-stage DOA estimation method for passive radar based on sparse representation①
Liu Nan (刘 楠), Song Wenlong②
(College of Mechanical and Electronic Engineering, Northeast Forestry University, Harbin 150040, P.R.China)
In a GPS illuminator based passive radar system, estimation of direction of arriving (DOA) of multiple targets is a difficult problem due to strong interference. A two-stage method combining extensive cancellation algorithm (ECA) and sparse representation is proposed. In the first stage, ECA algorithm is used to eliminate the direct-path and multi-path interference. In the second stage, sparse representation of improved weight constraints based on L1 norm is adopted to estimate DOA and suppress the interference. Simulation results show that the proposed method can effectively estimate DOA in low computation complexity without estimating the disturbance parameter.
passive radar, GPS illuminator, direction of arriving (DOA), extensive cancellation algorithm, sparse representation
0 Introduction
Passive radar is a radar system which exploits external non cooperative transmitter as the illuminator, receives signals reflected from the target, and extracts the source bearing, speed and other parameters[1]. GPS has the characteristics of all-weather, anti-interference and real-time, and the idea of using reflected signals from GPS for the passive radar, becomes a hotspot recently[2]. However, weak echo signal through an echo channel is inevitable interfered by direct wave, multipath signal and clutter sidelobe. How to make the direction of arriving (DOA) estimation of multiple targets in the interference has become an important content which must be solved.
To detect the multiple targets when applying interference suppression, many approaches have been presented. In Ref.[3], the method for interference suppression is accurate to dispose direct wave and multipath because of estimating the parameter of each disturbance, but it can not deal with echo sidelobe interference. The extensive cancellation algorithm (ECA)[4]progressively detects the strongest delayed and frequency shifted replicas of the direct signal and removes its effects on the received signal without parameter estimation, although the technique can not estimate direction. MUSIC-like[5]method uses a subspace
method of direction estimation which is more than the number of array element, applies fourth order cumulating matrix with high computational complexity. In Ref.[6], Sparse represents a signal processing theory as a rising thought system, can use high order accumulated to estimate DOA.
A two-stage DOA estimation method is proposed in this work. In the first stage, ECA is applied to remove the direct wave and mulipath interference. In the second stage, a sparse DOA estimation model is constructed with improved L1 norm as sparse constraint conditions. And the equilibrium constraint is applied to restrain the residual echo sidelobe jamming and decrease the computation complexity. The paper is organized as follows. Section 1 describes a system model and reference scenario. Section 2 derives an improved reweighted L1 norm sparse model and problem formulation. Section 3 describes the proposed algorithm as a processing procedure. Theoretical results are supported by numerical simulations, see Section 4. Finally the conclusions are drawn in Section 5.
1 System model
The system model is shown in Fig.1. In the figure, L is a base line, RTis the distance between the target and the radiation source, RRis the distance between the target and the receiver. α is the angle between the GPS satellite and ground, γ is the angle between the target and the receiver, θ is the angle betweenL and RR, v is the projection from target to ground with angle bisector φ.
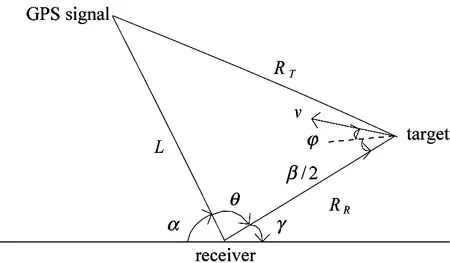
Fig.1 Space system model
The ambiguity function is
(1)
where, RR0, v0, τ0and fd0are the distance, speed, time delay and Doppler frequency shift of the initial target respectively. The receiving station is composed of reference channel and echo channel[7]. The reference channel uses standard GPS receivers to collect the direct signal. In the echo channel, the weak target echoes are embedded in the background of strong direct signal, multipath targets and multi target sidelobe jamming. In the echo channel, down conversion to an intermediate frequency is processed after amplification and filter. The two-stage DOA estimation method is proposed. In the first stage, ECA algorithm is used to eliminate the direct interference and multipath interference using time domain interference cancellation and zero Doppler subsidence. In the second stage, multi objective DOA estimation is completed in low SNR using L1 Norm as a constraint condition.
2 Two-stage DOA estimation
2.1 ECA algorithm
Different from the conventional interference suppression method, the signal from base station is projected onto orthogonal subspace with base station direct wave and time delay expansion space by ECA algorithm, instead of estimating interference parameter. In the ECA algorithm, segmented cancellation can eliminate not only direct wave and multipath interference of zero frequency, but also near zero frequency clutter. Consequently, in the first stage ECA algorithm is adopted to suppress direct wave and multipath interference.
In echo channel, the target echoes are submerged in the background including target echo, direct wave interference, multipath interference and other noises. The signal in the echo channel is

(2)
where, the first part is direct wave interference, the second part is multipath interference, the third part is target echo signal, and the last part is other noise in the channel. Suppose that in the two-dimensional correlation unit of R distance, the strongest reflected signal is k distance, then the delay reference array is
sref-k(t)=s(t)·D·F
(3)
where, D={dij} is Delay matrix, F is Doppler frequency shift matrix with P frequency points. The projection operator M is calculated by associative array sref-K(t). The target echo is projected to the interference space orthogonal subspaces by projection operator. And then echo is
ssur-E(t)=ssur(t)·[I-M(MHM)-1MH]
(4)

(5)
2.2 DOA estimation sparse representation
MUSIC-like method is proposed in Ref.[8] for multiple targets in a range-Doppler unit, which uses all four order comulation and subspace for direction finding. But this method requires information redundancy and high computation to coherent processing. Sparse representation for DOA estimation does not need signal coherence, therefore sparse representation is chosen for high accuracy and few snapshots. When the relationship between number of antenna array elements P and target number satisfied P≥uN0ln(N/N0), it is defined that the target space is a sparse structure[9]. Using sparse reconstruction, DOA of multiple target is accurately estimated with low computation complexity. The vectorization procedure of Eq.(5) is represented as
y=vec(ssur-E(τ, fd))=Aβ+n
(6)
where vec(·) is vector processing, y is the processed signal, β is a scalar matrix, A is a coefficient matrix whose components are [ejπsinθi…ejpπsinθi]T. It is known that under appropriate conditions, it is possible to solve Eq.(6) with a sparsity constraint as follows:
(7)
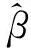
(8)
where, diagonal matrix ω whose component is
(9)
where, δ is threshold value, large coefficient will be more than δ, α controls the degree of the adjustment, η is impact factor of weight. By adjusting the above parameters, Eq.(9) can be applied to balance the constraint value with the goal of recovering sparse signal in low SNR.
3 Algorithm descriptions

Step 1: construct matrix A using ECA method according to Eq.(8)

Step 5: update α,η;
Step 6: k=k+1;
In the iterative process, the duality gap, gradient vector and Hesse matrix of the cost function O(L) is applied to determine the searching direction, dual gap is applied to determine the termination condition, and finally liner echo search algorithm is adopted to determine the optimal step size.
4 Computer simulation and complexity analysis
In order to analyze the performance, GPS signal is constructed as a radiation source in a range-Doppler unit, assuming SNR is -20dB, and the DOA of two goals is -1° and 5° respectively. Fig.2 shows the direction estimation result. Fig.3 shows the reconstruction probability of 5° goal while 1° goals remains the same. As shown in the figure, the correct rate is more than 98% when two goals are 5.1° apart. Fig.4 shows the probability estimation of two goals when SNR changes. It is obvious that this method can process target detection with SNR greater than -30dB. Fig.5 shows the correct rate when gradually adjusting the array element number and remaining SNR the same. As shown in the figure, DOA estimation accuracy is higher when

Fig.2 DOA result

Fig.3 Relationship between DOA estimation accuracy and correct rate

Fig.4 Relationship between SNR and correct rate

Fig.5 Relationship between the number of array element and correct rate
the number of array element is lager than 10 because of spatial sparsity.
In simulation, 8 multipath interferences appear in the region of 0~30km, with SINR of 50dB. The distance, Doppler shift , DOA and SNR of 4 targets are:
(20km, 1MHz, 20°, -8.04dB),(40km, 3MHz, 50°,-10.07dB),(70km,2MHz,80°,-17.28dB),(80km, -2MHz, 100°, -23.92dB). Fig.6 shows the range-Doppler correlation before processing interference suppression. As shown in Fig.6, target echo can not be detected because of channel interference. Fig.7 is zero Doppler section after ECA algorithm. ECA can eliminate interference within 10km to 60km. Fig.8 shows the contour of 2D correlation after processing ECA method for suppressing the direct wave and multipath in the region of 0~100km. Fig.9 shows the better effect detection after sparse representation. As shown in Fig.10, MSE(mean square error) of the method in this paper and Candes method is lower than that of MUSIC-like method. Fig.11 shows that the probability of resolution in this paper is higher than Candes method and MUSIC-like method. As shown in Fig.12, the RMSE (root mean square error) is stable when the threshold is less. When the threshold is greater than 0.3, RMSE increases for over constraint of much weight value.

Fig.6 Correlation before cancellation
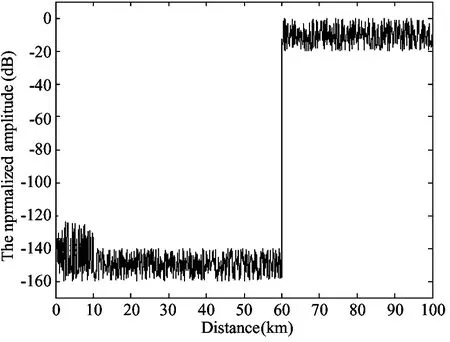
Fig.7 Zero Doppler section after ECA

Fig.8 2D correlation after ECA
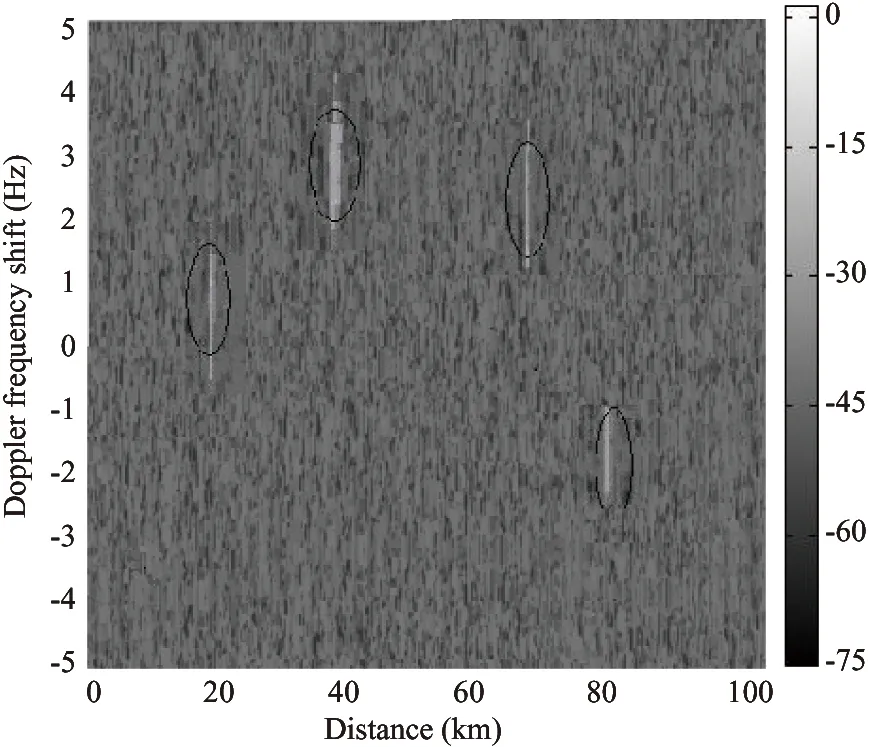
Fig.9 2D correlation after sparse representation

Fig.10 Mean square error curve
Assuming that array antenna with M element receives L snapshots, the complexity is O(LM3) in ECA algorithm and O(N3logN) in sparse reconstruction. The total complexity is O(LM3+N3logN). MUSIC-like method needs a number of multiplications and additions, whose order of complexity is O(M10+LM4+NM4). Therefore the complexity is lower based on sparse reconstruction.

Fig.11 Resolution probability curve
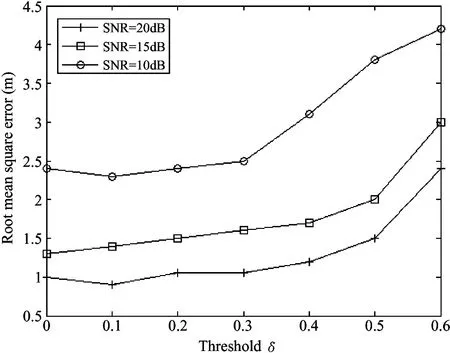
Fig.12 Relationship between threshold and RMSE
5 Conclusion
By analyzing interference factors of GPS for passive radar system, a DOA estimation based on improved weight L1 norm constraints is proposed. In the first stage ECA method can eliminate the direct and multipath interference. In the second stage, by adjusting the weight, DOA estimate accuracy is high in low SNR with less computation complexity.
Reference
[ 1] Radmard M, Karbasi S M. MIMO PCL in a single frequency network. Microwaves, Radar and Remote Sensing Symposium, 2011, 25(8) 280-283
[ 2] Idris A N, Suldi A M. Effect of radio frequency interference (RFI) on the Global Positioning System (GPS) signals. Signal Processing and its Applications, 2013, 3(10):199-204
[ 3] He D B, Wang X G. A study on passive radar target location using GPS signal. Gnss World of China, 2011,4(1):20-22
[ 4] Colone F, O’Hagan D W, Lombardo P, et al. A multistage processing algorithm for disturbance removal and target detection in passive bistatic radar. IEEE Transaction on Aerospace and Electronic Systems, 2009, 45(2):692-722
[ 5] Akkar S. MUSIC like algorithms for fast direction of arrival estimation. Advanced Technologies for Signal and Image Processing (ATSIP), 2014,3(10): 550-554
[ 6] Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 2006, 52(2): 489-509
[ 7] Wan L L, Zuo W H. Research on interference mitigation of GPS-based passive radar. Electronic Design Engineering, 2011,19(8):103-110
[ 8] Shan Z L, Ji F, Wei G. Extention Music-like Algorithm for DOA Estimation with more Sources than Sensors. Nanjing, China: Neural Networks & Signal Processing, 2003.14-17
[ 9] Julazadeh A. Classification based on sparse representation and Euclidian distance. Neural Networks, 2012, 10(3):11-16
[10] Candes E J, Wakin M B. An introduction to compressive sampling. IEEE Signal Processing Magazine, 2008, 25(2): 21-30
Liu Nan, born in 1980. She received his Ph.D degrees in Information and Communications Engineering Department of Harbin Engineering University in 2007. She also received his B.S. and M.S. degrees from Harbin Institute of Technology University in 2002 and 2004 respectively. Her research interests include the radio navigation and radar system.
10.3772/j.issn.1006-6748.2015.04.013
①Supported by the National Natural Science Foundation of China (No. 31270757), Specialized Research Fund for the Doctoral Program of Higher Education (No. 20110062110002) and the Fundamental Research Funds for the Central Universities (No. 2572014EB03, DL13BB16).
②To whom correspondence should be addressed. E-mail: wlsong139@126.com Received on Oct. 11, 2014, Dong Guanghui
杂志排行
High Technology Letters的其它文章
- Magnetometer calibration algorithm based on ellipsoid constraint①
- Study and application of vibrating wire strain gauge in monitoring cable tension of FAST cable-net①
- Service optimization in programmable cloud network①
- Motion mechanism analysis of two contacting rollers①
- Design of bilayer lengthened LDPC codes over expanded graph for relay channels①
- Effect of laser heating on the microstructure and hardness of TRIP590 advanced high strength steel used for roll forming①
