MPLPK: A mobile path localization protocol based on key nodes①
2015-04-17WangJiahao王佳昊
Wang Jiahao (王佳昊)
(*School of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu 611731, P.R.China)(**The Fifth Research Institute of Ministry of Information Industry, Guangzhou 510610, P.R.China)
MPLPK: A mobile path localization protocol based on key nodes①
Wang Jiahao (王佳昊)②
(*School of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu 611731, P.R.China)(**The Fifth Research Institute of Ministry of Information Industry, Guangzhou 510610, P.R.China)
To alleviate the localization error introduced by irregular sensor network deployment, a new mobile path localization based on key nodes (MPLPK) protocol is proposed. It can recognize all concave/convex nodes in the network as fixed anchor nodes, and simplify the following localization process based on these key nodes. The MPLPK protocol is composed of three steps. After all key nodes are found in the network, a mobile node applying improved minimum spanning tree (MST) algorithm is introduced to traverse and locate them. By taking the concave/convex nodes as anchors, the complexity of the irregular network can be degraded. And the simulation results demonstrate that MPLPK has 20% to 40% accuracy improvements than connectivity-based and anchor-free three-dimensional localization (CATL) and approximate convex decomposition based localization (ACDL).
concave, convex node, mobile anchor node, sensor network, localization
0 Introduction
Node localization is one of the key issues of wireless sensor network applications, especially for large-scale complex and irregular networks. A lot of research have been carried out about localization and localization rate in the recent study[1-3]. There has been growing interests in using connectivity information only to locate other unkown nodes in these algorithms. Multi-dimensional scaling (MDS) based localization techniques have been proved to compute positions of high accuracy with low node density[4]. It’s main advantage is that there is no need for a lot of anchor nodes and low positioning error. For example, A MDS based algorithm MDS-MAP takes a hop distance matrix between any two of these inner nodes as input, and works out a set of relative position coordinates for each node[5], which can map the relative coordinates to absolute coordinates with a few anchor nodes. Nevertheless, the accuracy of MDS-MAP depends heavily on the assumption that the hop-count distance between two nodes can correlate with their Euclidean distance. The assumption is valid only when the network is distributed in a convex field. But real sensor network deployment can hardly guarantee the requirement.
To avoid using hop-count distance between any two far-away nodes, some studies introduce landmark node to reduce the localization error in the irregular networks[6-10]. Among them, CATL is a representation solution which is proposed as a recent state-of-the-art localization algorithm[11]. The main idea of CATL is trying to identify concave nodes where the hop count of the shortest path between two nodes is greater than the true Euclidean distance. It takes use of an iterative concave-avoiding multilateration scheme to locate the unknown nodes and proposed schemes to avoid the concave node affect the localization error. The uniform deployment of anchor nodes decides the location accuracy of CATL. Furthermore, due to the iterative procedure, CATL has to suffer from error propagation. According to this problem, ACDL is proposed based on approximate convex decomposition, which decomposes the network into several convex subsections[12]. In each subsection, the hop-count distance between nodes can provide a good approximation of their Euclidean distance, and it utilizes MDS algorithm to compute relative coordinate of every node. ACDL finally unifies the locations of all subsections with a few anchor nodes. The ACDL can effectively avoid localization error due to concave node and it first proposes the definition of convex/concave node. Nevertheless, it depends on improved-MDS algorithm which has a complexity of O(N2), but also it needs several fixed anchor nodes proper-distributed in the network.
The study proposes a MPLPK protocol to localize unknown nodes with mobile anchor based on key nodes. We firstly define concave/convex nodes as key nodes which greatly impact the positioning result. The mobile anchor node is introduced to localize the selected key nodes. Finally, we use these key nodes as anchors to localize other unknown nodes. In our work, we can locate these key nodes without knowing their coordinates, which can avoid affection of non-uniform anchor distribution. Secondly we introduce an improved MST to produce mobile moving path, which can help minimize the cost of network localization process. Finally we use key nodes to localize other nodes, the computation complexity and cost is O(N), which is better than O(N2) of ACDL.
1 Finding the key nodes
In an irregular network topology, the concave/convex nodes have great impact on localization accuracy when we use range-free localization algorithms to localize unknown nodes. Therefore, take use of concave/convex nodes as key nodes in the localization process is a straight forward method to simplify the problem. The first step is to pick out all the key nodes in the network.
1.1 Key node recognition
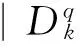

Fig.1 q is concave node, q1 and q2 is boundary node, node p is convex node, the green node is two-hop node from the node q

1.2 Finding all key nodes in network
To demonstrate the process of finding all the key nodes in an irregular network, Fig.2 is taken as an example and the nodes are assumed to be deployed in a simplified form. Firstly, every node tries to estimate whether itself is a boundary node or not. The black nodes around the network in Fig.2 represent boundary nodes. Secondly, all boundaries recognize themselves whether they are a concave/convex nodes and take them as key nodes. As shown in Fig.3, the black nodes represent the final selected concave/convex nodes.

Fig.2 Initial network
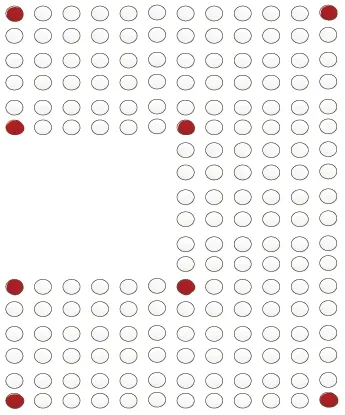
Fig.3 Find the key nodes
2 Localization of nodes
When the boundary nodes are recognized as shown in Fig.3, the localization problem of the whole network can be simplified into two steps, locate the key nodes and use them to position the rest ordinary nodes.
And most of all, the key issue of the method relies on how to effectively locate the black concave/convex nodes. To facilitate the work in real applications, a mobile anchor node is used to traverse all key nodes based on the planned moving path, and locate their positions. The path will be scheduled according to the key node distribution and no difference will be made with ordinary nodes.
2.1 Planning mobile path and locating key nodes
Due to the complexity of real application environment, wireless sensor networks are usually deployed in large geographical scopes with complex terrains. The path of the mobile anchor node needs to be carefully designed if it wants to traverse all the key nodes. A good path planning algorithm can effectively save the total path length and implementation cost of a mobile anchor node. The traversal of all key nodes is actually a special TSP (Traveling Salesman Problem), which is an NP-hard problem. Therefore, an improved minimum spanning tree (MST) introduced to accommodate the special TSP to solve the problem[15].
We generate the minimum spanning tree is generated by using the Prim algorithm and the path is simply adjusted among all key nodes, which can produce a unique and optimal path for the mobile anchor node. Our algorithm consists of the following steps:
(1) Computing the shortest path among all key nodes. Here it is assumed the boundary nodes of the network have been identified and the network is fully connected. The path is weighted as shown in Fig.4, and the shortest path is used as the weight among the key node graph.

Fig.4 Network with weight, all nodes in graph are key nodes
(2) Forming minimum spanning tree using Prim as shown in Fig.5.
(3) Deleting the connection between nodes whose degree is more than 2. Firstly a key node is randomly selected to start the traverse process. If the ith node’s degree is Wi>2, an edge with the node whose weight is the largest will be deleted until Wi≥2.
(4) Connecting the nodes whose degree is 0. The algorithm will check every key node’s degree. If the jth node’s degree is Wj=0, nodes whose degree W=0 or W=1 will be selected, and a node k is choosen which is closest to node j, and node j, k are connected at the same time, ++Wk,++Wj.
(5) After the 4th step, there should be no node with degree W=0. The algorithm will traverse all key nodes again to check nodes with the degree of W=1. It will select nodes whose degree is W=1 and connect the closest nodes together.
In the end, a fully connected Hamiltonian cycle can be achieved. As shown in Fig.6, the cycle describes the path used for mobile anchor node. And after the moving path planned, we can use the mobile anchor node to start moving in the network.
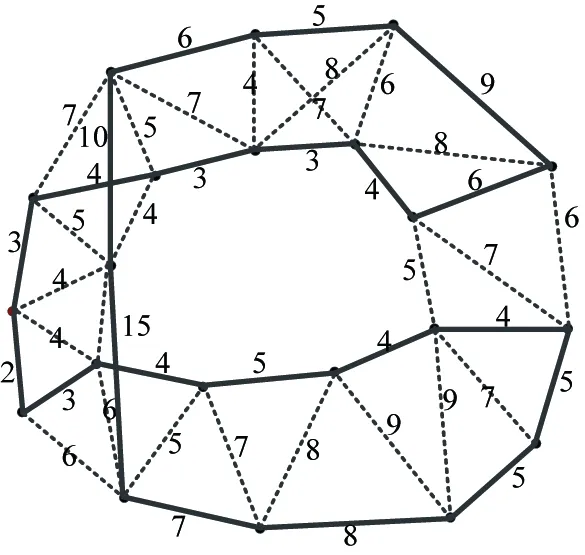
Fig.6 The shortest moving path
The key issue of key node localization is how to use the mobile anchor node effectively. Assuming there is only one anchor node each time, a more effective localization algorithm is introduced based on the solution provided in Ref.[16] and the mobile anchor node approaches the key nodes infinitely. The mobile anchor can usually detect the signal strength and direction. When the distance between the mobile anchor and unknown node is less than a threshold value close to 0, the coordinate of the mobile anchor node can be considered as the coordinate of the key node, and the localization of the key node is accomplished. The process is shown in Fig.7.
Positioning of key nodes in this method is not only accurate but also simple. It doesn’t require additional computing. Only a more accurate positioning equipment and signal detection device are needed to be installed on the mobile anchor. The method is comparably more applicable in real applications, and the MST based path planning algorithm can effectively improve the efficiency of the process.
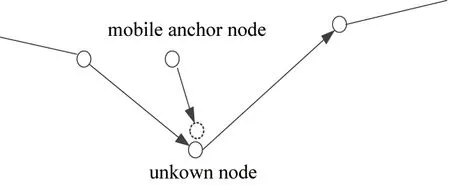
Fig.7 Localization of key node
2.2 Positioning ordinary node
After the key nodes are localized by the mobile anchor node, they can be used to locate other normal nodes. Concave nodes should exist if convex nodes appear at network boundary. Therefore, there should have no isolated node exist.
Definition 1:
Positioning directly:If there is a shortest path existing from a key node to an unknown node, and the path does not contain other key nodes, it is declared that the key node can locate the unknown node directly. Otherwise, it will locate the unknown node indirectly.
As shown in Fig.8, the shortest path between key node B and unknown node s doesn’t consist of other key nodes. Node B can be used to position node s directly, but node A can only contribute indirectly. The pseudo process of the algorithm is as:

Algorithm1:Seekingthenodessetwhichcanpositiontheunkownnodedirectly 1.C[N]asthekeynodesset,Nasthenumberofkeynodesset; 2.Setsastheunknownnode; 3.Ps[]asthekeynodessetwhichcanpositionsdi-rectly; 4.Lij[M]asthenodesetintheshortestpathbe-tweennodesiandj(exceptnodeiandnodej),MasthenumberofLij[M]; 5.fori=0toNdo 6 calculatingtheLis[]usingtheshortestpathal-gorithm; 7 forj=0toMdo 8 ifLis[j]∈C[N]thenC[i]cannotlocatenodesdirectly; 9 endfor 10 addC[i]inPs[]; 11 endfor
After getting Ps[] through Algorithm 1, distance d between unknown node s and every node could be calculated from Ps[] using range free locating algorithm like
d=Hhopsize×N
(1)
where Hhopsizerepresents the average hop distance of the entire network, which is relevant to the network density. N represents the number of hops between the key node and the target unknown node.
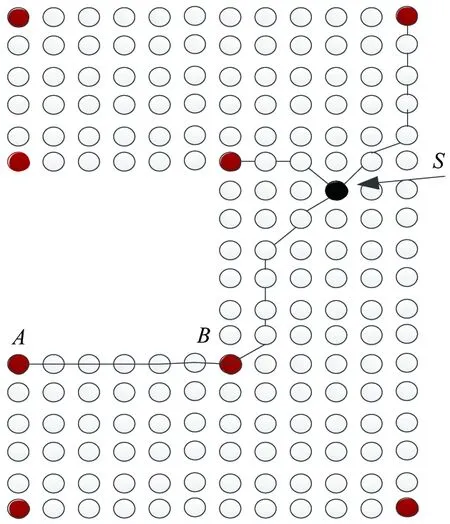
Fig.8 Positioning directly
Assuming ds1, ds2, ds3,…,dsirepresent the distances between unknown node s and the node in {Ps[1](x1,y1),Ps[2](x2,y2),Ps[3](x3,y3),…,Ps[i](xi,yi)} respectively. The node’s coordinate can be calculated as
(2)
3 Simulation
The simulation of the above mechanisms is implemented on a 1000m×1000m scene with n=1000 to n=2000 randomly distributed nodes. The entire network is full connected, the distance error ranges from 5% to 10% and the node communication radius r is set to 100 m and k=2.
The proposed MPLPK algorithm is compared with CATL and ACDL in our test. And the average localization error (ALE) and energy consumption results of the three algorithms are shown as below. Table 1 shows the comparison of their localization errors under ALE, 5-percentile, 50-percentile and 95-percentile.
From Table 1, It can be found that the proposed solution can achieve less localization errors than ACDL and CATL in different criteria. After implementing a mobile anchor node in key node localization process, our solution can effectively reduce location error 20% to 40% to the other two algorithms.

Table 1 Localization of CATL, ACDL and MPLPK
Table 2 compares the energy consumption level of the three algorithms. The results show that our algorithm can prolong the life of the entire network for it does not depend on fixed landmark node with energy consuming devices like GPS. Effective MST algorithm can greatly reduce energy consumption level for the mobile anchor node.
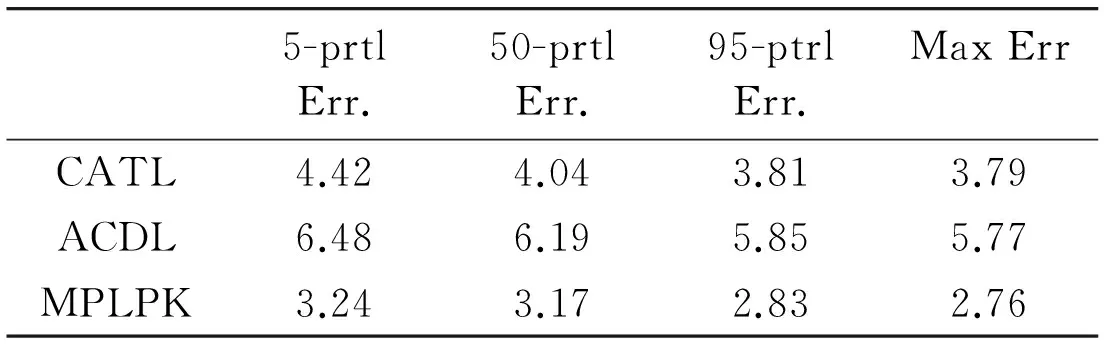
Table 2 Energy consumption
4 Conclusion
In this study, a new key node localization protocol MPLPK is proposed for wireless sensor networks with irregular topology. By identifying all concave and convex nodes in the network as key nodes, it simplifies the network deployment at first, and further takes use of them as fixed anchors to position other sensor nodes. To locate the key nodes, a MST based path planning algorithm is provided for defining mobile anchor node’s movement, which can avoid the localization error caused by concave nodes.
Here an optimized solution is provided for the irregular deployed network on the view of application. For complex network distribution, more optimization methods should be considered to simplify the implementation in real environments.
[ 1] Liu Y, Yang Z, Wang X, et al. Location, localization, and localizability. Journal of Computer Science and Technology, 2010, 25(2): 274-297
[ 2] Wang R J, Bao H L, Chen D J, et al. 3D-CCD: a Novel 3D Localization Algorithm Based on Concave/Convex Decomposition and Layering Scheme in WSNs. Ad Hoc & Sensor Wireless Networks. 2012, 0, 1-20
[ 3] Xu Y B, Sun Y L, Ma L. A KNN-based two-step fuzzy clustering weighted algorithm for WLAN indoor positioning. High Technology Letters, 2011, 17(3):223-229
[ 4] Ingwer B, Patrick J F G. Modern Multidimensional Scaling, Theory and Applications. Springer-Verlag, NewYork, 1997
[ 5] Shang Y, Ruml W, Zhang Y, et al. Localization from mere connectivity. In: Proceedings of the 4th ACM International Symposium on Mobile Adhoc Networking & Computing, Annapolis, USA, 2003. 201-212
[ 6] Bulusu N, Heidemann J, Estrin D. GPS-less low-cost outdoor localization for very small devices. Personal Communications, IEEE, 2000, 7(5): 28-34
[ 7] Jin M, Xia S, Wu H, et al. Scalable and fully distributed localization with mere connectivity. Proceedings of IEEE INFOCOM, Shanghai China, 2011. 3164-3172
[ 8] Lederer S, Wang Y, Gao J. Connectivity-based localization of large scale sensor networks with complex shape. Proceedings of IEEE INFOCOM, Phoenix, USA, 2008. 789-797
[ 9] Tang T, Qing G. Node cooperation based location secure verification algorithm in wireless sensor networks localization. High Technology Letters, 2012, 18(4):376-381
[10] Wang Y, Lederer S, Gao J. Connectivity-based sensor network localization with incremental delaunay refinement method. Proceedings of IEEE INFOCOM. Rio de Janeiro, Brazil, 2009. 2401-2409
[11] Tan G, Jiang H, Zhang S, et al. Connectivity-based and anchor-free localization in large-scale 2d/3d sensor networks. Mobihoc 2010, Chicago, USA, 2010. 191-200
[12] Liu W, Wang D, Jiang H, et al. Approximate convex decomposition based localization in wireless sensor networks. In: Proceedings of the IEEE INFOCOM 2012, Orlando, USA, 2012. 1853-1861
[13] Dong D, Liu Y, Liao X. Fine-grained boundary recognition in wireless ad hoc and sensor networks by topological methods. In: Proceedings of ACM MobiHoc 2009, New Orleans, USA, 2009. 135-144
[14] Wang Y G, Jie M, et al. Boundary recognition in sensor networks by topological methods. In: Proceedings of ACM MobiCom 2006, Los Angeles, USA, 2006. 123-133
[15] Zhao Y. An improved spanning tree algorithm for solving the Traveling Salesman Problem. Journal of Lanzhou University, 2008, 44: 164-165, 168
[16] Li S J. Research on Localization Algorithm for Wireless Sensor Network in Three-Dimensional Space: [Masters dissertation]. ECUST, 2012
Wang Jiahao, born in 1978, is an Associate Professor at University of Electronic Science and Technology of China(UESTC). He received his Msc and Ph.D Degree from UESTC in 2004 and 2007 respectively. His research interests includes RFID security, RFID&WSN integrated identifying and tracking, etc.
10.3772/j.issn.1006-6748.2015.02.002
①Supported by the National Natural Science Foundation of China (No. 61133016), the Sichuan Science and Technology Support Project(No. 2013GZ0022), the Scientific Research Fund of Xinjiang Provincial Education Department (No. XJEDU2013I28) and the Technology Supporting Xinjiang Project (No. 201491121).
②To whom correspondence should be addressed. E-mail: wangjh@uestc.edu.cn Received on Feb. 10, 2014*, Bao Honglai*, Yang Xiaoming***, Wang Ruijin*, Qin Zhiguang*
杂志排行
High Technology Letters的其它文章
- Improving wavelet reconstruction algorithm to achieve comprehensive application of thermal infrared remote sensing data from TM and MODIS①
- Security analysis of access control model in hybrid cloud based on security entropy①
- Multi-sensor federated unscented Kalman filtering algorithm in intermittent observations①
- Research on suppress vibration of rotor misalignment with shear viscous damper①
- Design and development of real-time query platform for big data based on hadoop①
- A method for retrieving soil moisture from GNSS-Rby using experiment data①
