MSA在快捷式身高测量系统设计中的应用

2015-04-17武文慧

东南大学学报(哲学社会科学版) 2015年2期

武文慧

（天津工业大学管理学院，天津 300380）

身高还为各种工业设计、机械设备、建筑家具、空间安排提供了设计的基础，其中心思想就是满足人的需求，在保证安全的情况下，提高生产效率或进行艺术创造。因此，对于如何快速准确的获取测量对象的身高，人们开始研发各种各样的身高测量仪器。

根据对A实验室深入研究和探索，以及各类传感器的特点的了解，发现可以利用F传感器来测量人体身高，以达到将A实验室用到实际中去的目的，从而设计了便捷式身高测量系统。通过对便捷式身高测量系统进行测量系统分析，得出该测量系统是可用的，虽然测量距离与实际距离之间存在一些偏差，但是可通过回归方程来纠正这一偏差，使其线性偏倚变得可接受。最后进行实用性分析，发现快捷式身高测量仪器在实际使用过程中，能够准确有效的获取的人体身高数据。并且此测量系统更简单，快捷，方便，弥补了传统身高测量仪测量过程存在的麻烦、消耗时间长等不足。

一、快捷式身高测量系统的设计

（一）设计方案

将A实验室应用于实践，而不是局限于实验教学。在对其进行探索研究的过程中，发现可以利用F传感器的原理及特点来测量人的身高。因此利用C计算器、B盒子和F传感器制作一个人体身高测量系统，如图1所示。

图1 身高测量仪模拟图

（二）原理及过程

本次制作的模型，出于方便，直接将F传感器固定在传统的身高测量仪器上，如图2所示。一侧为传统的身高测量仪，一侧为用A实验室的器材制作的高度测量仪器，可方便采集数据，以及对比。原理：将F传感器固定在一定的高度上，系统准确的测量F传感器到人头顶的距离，再由这个一定高度计算出人体身高。传统身高测量仪的标注刻度最大为2米，实际高度为2.15米，考虑到F传感器的测量范围是0.2至10米，这个一定的高度选取2.127米，即可满足绝大多数人的身高测量需求。

图2 身高测量仪器实物图

设备安装：

1.F传感器连接B盒子通道1。2.B盒子的插头连接到C计算器上。打开计算器。3.打开B盒子。4.按开始键，使用方向键。为了便于收集数据，在电脑上安装了D虚拟软件。将C计算器上的USB接口直接连接到电脑上。使用E系统采集数据，如图3所示。

图3 E系统

身高测量仪器设计制造完成后，主要任务就是来分析这个量具是否可用，以及其精密度与准确度，还有与传统的身高测量仪器相比，是否存在优势。那么首先对量具进行测量系统分析。

二、测量系统分析

测量系统分析（MSA），用于评估测量系统的质量，是运用统计方法来分析研究测量系统中的各个变差源以及它们对测量结果的贡献，并根据可接受的判断方法判断测量系统的符合性。

（一）试验方案制定

图4 测量高度

我们小组三人作为本次试验的操作员，并编号为A、B、C。每个操作人员对每个高度测量3次，设计一个3310的试验。测量过程如图4。

1.用Minitab制作随机表，由主持人按照随机表的顺序，安排操作人员进行盲测。

2.记录测得的数据和整个测量过程，进行线性和偏倚分析并得出相应结论。

（二）试验数据采集和测量系统分析

针对测量系统分析的数据采集，主要使用C计算器读取数据，便于直观的读出某个点的数据。

采集的数据导入Minitab中，并进行计算得出相关结果。

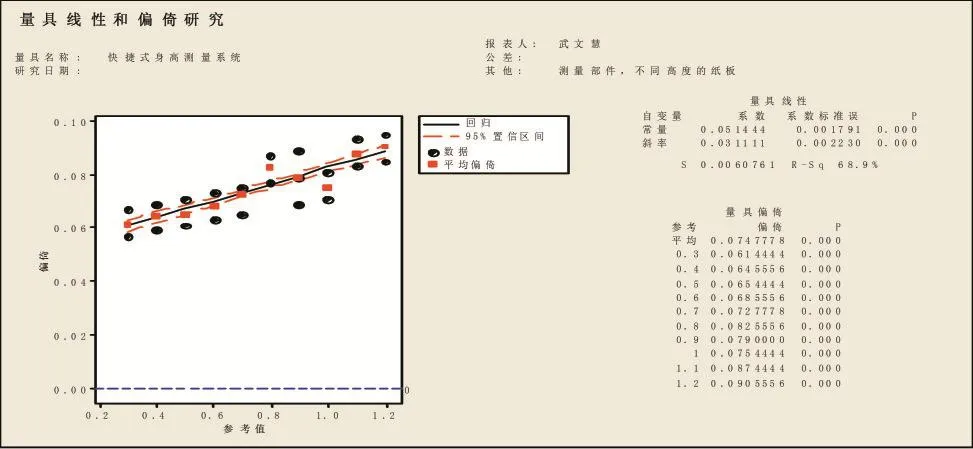
图5 线性偏移分析图

由线性偏移分析图可看出，如图5所示，量具偏倚平均的P值为0，小于0.05，根据测量系统分析判定标准可知存在显著的偏倚问题。回归线性的斜率为0.031111，P值为0，小于0.05，根据测量系统分析判定标准可知存在显著的线性问题。认为该测量系统的线性偏倚是不可接受的。究其原因，排除量具故障的可能性，主要就是量具自身缺乏稳健性，所以要对其测量结果进行线性回归分析，以弥补量具自身的不足。

（三）回归分析

测量系统存在明显的线性偏倚，对其进行回归分析并得出相应结果。将线性偏倚研究中的数据导入Minitab中，进行分析。如图6所示。

图6 回归分析

通过回归方程，根据测量数据计算出实际距离′（实际距离′=0.969测量距离-0.0496），重新收集数据导入Minitab中，并进行计算得出相应结果。

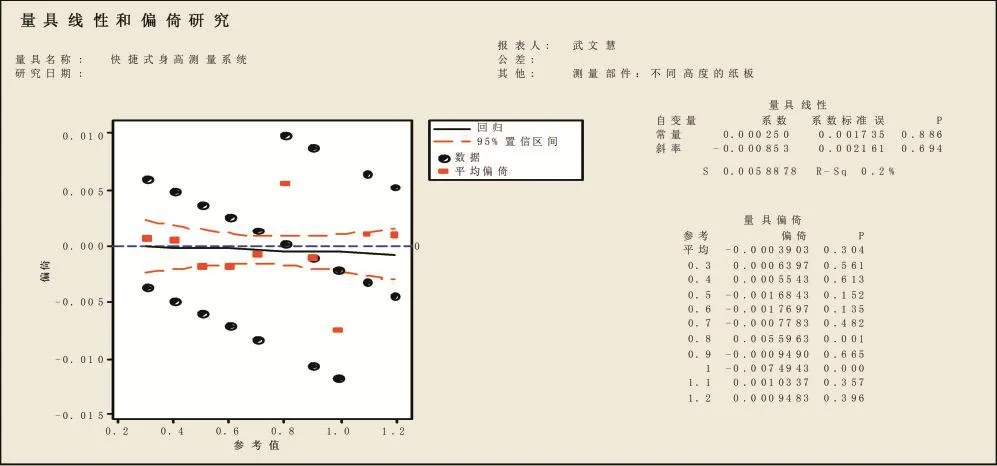
图7 实际距离′的线性偏移分析图

由实际距离′的线性偏倚分析图可看出，如图7所示，量具偏倚平均的P值为0.304，远大于0.05，根据测量系统分析判定标准可知不存在显著的偏倚问题。回归线性的斜率为0.000853，接近于零，P值为0.886，远大于0.05，根据测量系统分析判定标准可知不存在显著的线性问题。故认为经过引入回归方程，该测量系统的线性偏倚变得可接受。

三、测量系统的实用性分析

（一）身高测量仪的使用及分析

经过对制作的身高测量仪器进行的测量系统分析，该测量系统是可用的，虽然测量距离与实际距离之间存在较大的偏差，但是可通过回归方程来纠正这一偏差，使其线性偏倚变得可接受。

为了再次验证高度测量仪器的实用性，对本组成员A、B、C三人进行身高测量。在数据收集过程中，为了便于观察，采用电脑上安装的MCL虚拟软件中的“探世界”实验室系统-傅氏系统进行数据收集。如图8所示，是对A同学进行测量时，用电脑收集的图形。

图8 软件收集数据

采集数据，经过回归方程计算，得到测量高度，与A、B、C三人实际身高相比（实际高度是由传统的身高测量仪器测得的数据），误差仅在1-2毫米内。如表1所示。

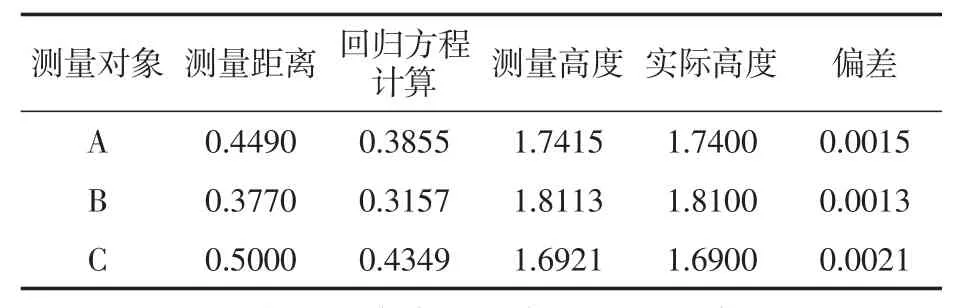
表1 身高测量数据

由以上所示，快捷式身高测量仪器在实际使用过程中，能够准确有效的获取的人体身高数据。被测者只需站在F传感器下方一秒的时间，就能用E系统的数据，将其导入到EXCEL中，通过公式计算，得出被测者的身高。这种方法简单，快捷，方便，其最大的有点就是节省时间。

（二）存在的问题及解决方案

在测量过程中，发现了一系列的问题。

1.测量身高的过程中，头发对测量结果有一定程度的影响。F传感器主要是靠超声波来测量被测对象到传感器的距离，头发的松散程度影响了测量结果，这个影响因素属于不可避免的，也是因人而异的。所以在此次测量身高的过程中，我选择在被测对象的头顶上放一张薄纸，可以保持头顶的一个水平高度，其次因为纸薄，基本上对测量结果不会有较大的影响。

2.E系统或者C计算器收集数据时，从图形中明显可以看出测量得到的数据并不是一个稳定的数值，而是有一定的上下波动范围。经多次测量发现，这个波动为上下1厘米。本文中，在进行测量系统分析中收集的数据，使用的C计算器，操作者根据自己的选择读取一个数据。在身高测量过程中，使用的是E系统，如图4-1所示，收集的数据呈上下波动状态，通过对数据的观察，选取众数（出现频率最大的数）作为测量结果进行分析。