分布相关的曲波阈值超声图像去噪方法

徐 杰，崔崤峣，向永嘉，吕铁军，顾天明

XU Jie1，2，3,CUI Yaoyao1,XIANG Yongjia1,LV Tiejun1,GU Tianming1

1.中国科学院 苏州生物医学工程技术研究所，江苏 苏州215163

2.中国科学院大学，北京100049

3.中国科学院 长春光学精密机械与物理研究所，长春130033

1.Suzhou Institute of Biomedical Engineering and Technology,CAS,Suzhou,Jiangsu 215163,China

2.University of Chinese Academy of Sciences,Beijing 100049,China

3.Changchun Institute of Optics,Fine Mechanics and Physics,CAS,Changchun 130033,China

1 引言

超声医学成像广泛应用于临床诊断，具有低成本、实时性等优点，能够配合MRI、X-CT等手段，利用图像引导、图像配准和图像融合等技术实现更好诊断效果[1]。这对超声图像质量提出了更高要求。

超声成像信号中包含的随机性的散射信号导致生成图像中含有散斑噪声，直接影响图像质量，对图像进行去噪增强，提高信噪比，滤除成像噪声干扰，是进一步分析和计算的基础[1]。常见的去噪方法包括以中值滤波和维纳滤波为代表的空域方法和以小波去噪为代表的多尺度分析方法。单尺度的空域方法相对多尺度分析方法，不能准确描述噪声信息，去噪过程信息损失较大。小波方法具有局部时频特性和多分辨特性特点，在图像去噪中广泛应用，但小波变换对边缘、纹理的表达能力有限，直接影响了去噪效果[2]。针对小波变换的局限性，Candès 等提出了曲波方法[3]，实现对信号稳定、高效和近乎最优的表示[4]，能更好地分离去除信号噪声。Donoho 文中使用硬阈值和软阈值方法[5]，为改进硬阈值的不连续性和软阈值恒定偏差的问题，后续还提出半软阈值[6]和渐进半软阈值[7]等方法，但以上方法在对于小于阈值λ的系数处理较为粗糙，使得图像中部分细节丢失，去噪性能下降。

本文针对上述问题，依据曲波噪声系数与噪声分布的相关性，利用噪声分布特点构造合适的曲波系数阈值方法，在减少图像信息损失条件下，合理去除曲波系数中的噪声系数，进一步提高曲波去噪方法的去噪性能。

2 实验方法

2.1 曲波变换

曲波变换通过曲波函数与信号f的内积，将信号分解为在不同尺度j、角度l、位置k的曲波系数矩阵{wj,l,k}，其中φj,l,k表示曲波基函数。

根据连续曲波变换方法，离散曲波方法如式（2），其中离散f[t1,t2]、φj,l,k[t1,t2]对应连续变换方法中f(x)、φj,l,k(x)，0 ≤t1,t2＜n。

在曲波变换理论基础上，Candès 等提出快速离散曲波变换（FDCT）方法[3]：USFFT 方法和Wrapping 方法。本文针对超声图像中噪声，使用二维离散快速曲波变换Wrapping（WFDCT）方法对含噪图像进行处理。曲波去噪分为曲波分解、噪声水平估计、阈值处理、图像重构四个步骤。

2.2 超声图像噪声

超声图像中固有噪声主要散斑噪声，散斑噪声模型中加性噪声ηα的影响和乘性噪声ηm相比可以忽略[1]。实际超声成像过程中，原始超声回波信号经过对数压缩放大、线性增益成像[8]，如式（3），A为放大率，g(t1,t2)为原始不含噪声信号，LGC为线性增益常数，Nf为不含噪声部分。

由散斑噪声符合瑞利分布得出实际超声图像中噪声N=A·ln(ηm(t1,t2))概率密度如式（4）：

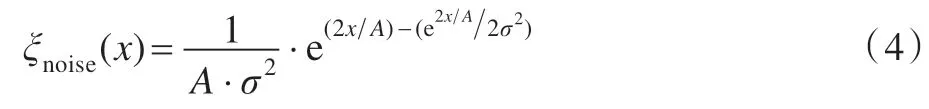
2.3 噪声水平估计

文中，定义图像中噪声X=Nf+D·N，其中D为噪声强度，N为均值为1 的噪声。

曲波去噪方法通过曲波子带系数{wj,l,k}对图像中的噪声水平D进行估计，估计值为λ，文中采用的估计方法计算式为[9]：

2.4 阈值函数

曲波阈值去噪方法通过对分解系数wj,l,k进行相应的阈值处理，滤除分解系数中的噪声系数。为反映阈值方法对分解系数的处理过程，定义曲波分解系数中的噪声水平Δρj,l,k如式（6），其中为阈值处理后曲波系数。

常用阈值设定四种方法：硬阈值[9]、软阈值[9]、半软阈值[6]、渐进半软阈值[7]。

超声信号经曲波方法（2）得到图像的曲波分解系数矩阵{wj,l,k}，分解系数中噪声信号系数的分布与原信号中噪声信号N分布有关。

曲波变换对数据中部分信号进行部分抽取分析时，噪声信号的曲波系数分布具有原信号噪声分布的特点。根据实际超声信号中散斑噪声分布的概率密度函数（4），保证分解尺度、角度的一致，构造式（8），其中H(x)为变换函数，κ为曲波变换引起的放缩系数，ε为调整含有噪声阈值区间的调整系数，在测试中取κ=2，具有较好的去噪效果。

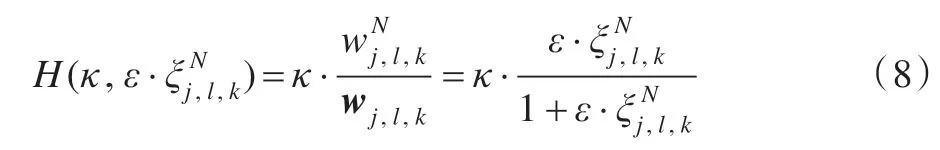
为验证噪声分布相关阈值方法，建立加性高斯白噪声噪声图像模型X=Nf+D·GN，其中GN为符合N～(0,1)分布高斯白噪声。根据据高斯白噪声概率密度曲线构造阈值函数。

根据构造函数，得到简单加性高斯白噪声基于噪声分布相关阈值方法有如下关系：

以上几种阈值方法wj,l,k～Δρj,l,k曲线的变化特点如图1 所示。

图1 阈值方法wj,k,l～Δρj,k,l 曲线对比

根据图中曲线变化趋势，分布相关阈值方法相较软阈值、折衷阈值以及渐进阈值方法收敛速度更快，并且不存在硬阈值方法不连续的缺点。

3 实验与分析

为评价不同去噪方法对散斑噪声和高斯白噪声的去除水平，使用平均结构相似度[10]（Mean Structural Similarity Index Map，MSSIM）和峰值信噪比[10]（Peak Signal to Noise Ratio，PSNR）。其中MSSIM直接反映与原图像的相似程度，为主要参考指标。

实验采用Ultrasonix 公司的SonixTouch 超声系统采集，包含不同程度噪声的人体颈动脉超声图像作为实验对象。使用均值滤波、维纳滤波、小波阈值去噪和曲波阈值去噪方法评价不同方法的去噪能力；使用基于曲波的硬阈值、软阈值、折衷阈值、渐进阈值和基于噪声分布阈值方法评价曲波方法不同的阈值处理过程去噪能力。

实验中值滤波和维纳滤波，选取3×3 模版；半软阈值系数α和分布相关参数ε、σ对去噪效果有一定的影响，选取相应噪声水平下最佳的参数进行图像去噪。

分别对含有不同程度噪声水平D的去噪对象进行相应去噪处理。不同去噪方法对去噪对象中散斑噪声处理结果见表1；不同去噪方法对去噪对象中加性高斯白噪声处理结果见表2。

表1 不同去噪方法去噪性能（散斑噪声）

表2 不同去噪方法去噪性能（高斯噪声）

在不同去噪方法上：较低噪声水平下不同去噪方法都具有较好的去噪效果，但较高噪声水平下，传统的空域去噪方法、中值滤波以及维纳滤波的PSNR和MSSIM有明显程度的下降，去噪效果不稳定；多分辨分析方法中小波以及曲波去噪方法在不同噪声水平下都能提供较为稳定的去噪性能；多分辨分析方法中相较小波方法，曲波方法平均的去噪效果优于小波方法。

在基于不同阈值方法的曲波去噪方法：两种分布相关的阈值方法在处理不同噪声水平的图像时，其PSNR和MSSIM较其他阈值方法有较大的提升；基于不同噪声分布相关的去噪方法对具有相应的噪声图像有更好的去噪效果。

图2 分别显示颈动脉超声图像的含噪图像、中值滤波、dB5 小波和分布相关阈值方法对散斑噪声去除的实际成像效果，噪声水平选取D=35。图中直观看去噪效果，分布相关阈值具有更好的去噪性能。

图2 颈动脉超声图像去噪效果

另使用Lena标准测试图作为测试对象，测试去噪后图像细节的损失，图3为含噪图像、中值滤波、dB5小波、分布相关阈值方法去噪效果对比，噪声水平选取D=35。

图3 Lena图去噪效果对比

在不同噪声水平下，中值滤波、维纳滤波、dB5 小波、硬阈值方法、散斑分布相关阈值方法的去除散斑噪声性能PSNR和MSSIM变化趋势如图4 所示；中值滤波、维纳滤波、dB5 小波、硬阈值方法、高斯分布相关阈值方法的去除加性高斯噪声性能PSNR和MSSIM变化趋势如图5 所示。根据图中PSNR和MSSIM变化趋势，本文提出的基于噪声分布相关阈值方法相较其他方法具有稳定的去噪性能，相较其他去噪方法和曲波阈值方法，去噪效果有较明显的提升。

图4 不同去噪方法去除散斑噪声性能

图5 不同去噪方法去除高斯噪声性能

4 结论

本文主要针对超声图像中的散斑噪声，在去噪方法上与传统的中值滤波、维纳滤波和小波进行对比，曲波方法能更好地去除图像中的噪声；在阈值方法上提出了基于散斑噪声分布相关的曲波阈值方法，根据噪声信号的分布特点，建立合适的阈值函数处理曲波分解系数中噪声系数，进一步提升曲波阈值方法的去噪效果。实验结果表明，提出的基于噪声分布相关的阈值去噪方法较其他算法，去噪效果有较大的提升，其中相对硬阈值方法PSNR提升1～2 dB，MSSIM也有一定的提高，验证了本文提出噪声分布相关曲波阈值去噪方法的有效性，提供了一种稳定优异的超声阈值去噪方法。

[1] 万明习，宗瑜瑾，王素品.生物医学超声学[M].北京：科学出版社，2010：531-544.

[2] Devarapu K V，Murala S，Kumar V.Denoising of Ultrasound Images using Curvelet Transform[C]//Proceedings of the 2nd International Conference on Computer and Automation Engineering（ICCAE），2011：447-451.

[3] Candès E，Demanet L，Donoho D，et al.Fast discrete curvelet transforms[J].Multiscale Modeling & Simulation，2006，5（3）：861-899.

[4] 李伟，杨航.曲波域经验Wiener 滤波[J].吉林大学学报：理学版，2013，51（2）：312-316.

[5] Candès E，Demanet L，Ying L.CurveLab toolbox user’s guide.Version 2.0.3.

[6] 栗明，郭东敏，权建峰，等.基于提升小波的改进半软阈值降噪方法[J].探测与控制学报，2009，31（4）：54-57.

[7] 周西峰，朱文文，郭前岗.基于渐近半软阈值函数的超声信号去噪方法[J].探测与控制学报，2011，33（2）：35-39.

[8] Chen Y，Raheja A.Wavelet lifting for speckle noise reduction in ultrasound images[C]//Proceedings of the Conference on Engineering in Medicine and Biology Society（IEEE-EMBS 2005），2005：3129-3132.

[9] 王文波，羿旭明，费浦生.基于曲波系数相关性的去噪算法[J].光电子·激光，2006（12）：1520-1521.

[10] Wang Z，Alan C，Sheikh H R，et al.Image quality assessment：from error visibility to structural similarity[J].IEEE Transactions on Image Processing，2004，13（4）：1-14.

[11] Lazrag H，Naceur M S.Despeckling of intravascular ultrasound images using curvelet transform[C]//Proceedings of the 6th International Conference on Sciences of Electronics，Technologies of Information and Telecommunications（SETIT），2012：365-369.

[12] Yousefi Rizi F，Ahmadi Noubari H，Setarehdan S K.Waveletbased ultrasound image denoising：Performance analysis and comparison[C]//Proceedings of IEEE EMBS Annual International Conference，2011.

[13] Rabbani H，Vafadust M，Abolmaesumi P.Speckle noise reduction of medical ultrasound images in complex wavelet domain using mixture priors[J].IEEE Transactions on Biomedical Engineering，2008，55（9）：2152-2160.

[14] Gupta S，Chauhan R C，Saxena S C.A wavelet based statistical，approach for speckle reduction in medical ultrasound images[J].IEE J Int Fed Med Biol Eng，2004，42：189-192.

[15] Rabbani H，Vafadust M，Selesnick I，et al.Image denoising employing a mixture of circular symmetric Laplacian models with local parameters in complex wavelet domain[C]//Proc of ICASSP 2007，2007：805-806.