轨道视觉检测系统中行程编码的应用研究

闵永智，康 飞，党建武，邓 岳

MIN Yongzhi1,KANG Fei1,DANG Jianwu1,DENG Yue2

1.兰州交通大学 自动化与电气工程学院，兰州730070

2.中国北车集团 大连机车车辆有限公司，辽宁 大连116000

1.School of Automation and Electrical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

2.Dalian Locomotive and Rolling Stock CO.,LTD.CNR Group,Dalian,Liaoning 116000,China

1 引言

随着我国铁路建设的快速发展，铁路客货运输呈现高速重载发展趋势，而保障运输安全的前提是线路质量安全。在工务养护过程中，常采用视觉检测方案检查轨道病害、指导线路维修、保障行车安全。轨道视觉检测系统图像预处理过程中的阈值分割会造成轨道轮廓产生“断线”和“边缘毛刺”现象。该现象主要采用形态学运算中的膨胀处理来进行消除，而该过程需要进行大量的卷积运算且运算量极大。因此，本文采用行程编码方法对形态学膨胀过程进行优化。该方法具有不考虑背景区域仅描述核心区域，不考虑内部区域仅针对边界区域的特点。此外，存在图像区域逻辑交、并的简单运算是该方法对形态学膨胀进行有效优化的另一重要优势[1]。目前对于行程编码对形态学膨胀算法的优化研究中，文献[2]分别从运行内存与运算时间的角度验证了基于行程编码法的形态学膨胀在运算效率上的优势。Trein 等人的研究提出了一种基于FPGA 的行程编码运算逻辑电路，实现了行程编码算法优化的图像数据在硬件上的高速执行与并行输入[3]。文献[4]根据行程编码的连通关系链接节点形成边界并在切削层上构造物体区域的行程编码，从而得到切削区域的拓扑结构。吴铮提出了一种基于形态学膨胀运算和行程编码的新型小波编码器，有效地提高了数学形态学用于二值图像处理的速度[5]。因此，基于行程编码优化的形态学膨胀算法能够有效提高图像预处理速度，同时在硬件上易于高速处理和实现。

2 轨道视觉检测系统原理

传统的接触式轨道检测设备由于故障率高，检测精度差、抗干扰性差等原因已经逐步被非接触式的视觉检测方案所取代[6]。轨道视觉检测系统主要利用机器视觉原理提取轨道横断面几何参数，并结合多传感器数据融合进行参数修正，轨道质量通过轨道横断面几何参数判断。图1 为轨道视觉检测系统示意图，该系统主要由CCD 高速摄像机与线激光源组成。CCD 高速摄像机通过识别线激光光源在轨道表面法向的反射成像生成原始图像数据，再通过一系列算法得到轨道横断面单像素轮廓。

图1 轨道视觉检测系统原理示意图

经过多年的发展，针对轨道视觉检测系统的研究不断完善，但研究内容与侧重各不相同。许贵阳等开发的基于机器视觉的车载轨道巡检系统主要运用主成分分析等建模方法对轨道病害进行模式识别检测处理[7]。伏思华等设计出一种由测量主车和测量靶车两部分组成的基于合作标志方法的新型轨道几何参数测量系统[8]。文献[9]提出利用DLT 和CSS 角点算法对钢轨轨头磨耗进行检测。这些研究多侧重于轨道视觉检测系统的模型建立，系统搭建与后端实现。但目前针对轨道视觉检测系统前端图像预处理过程与算法处理实时性的深入研究尚无详细表述。

在轨道视觉检测设备中图像数据信息量巨大，因此图像处理算法的速度是制约系统整体检测性能的关键。而在图像处理的各个流程中，图像的预处理用于抑制无效信息，增强有效特征，要占据绝大部分的帧处理时间和运算内存，而后期算法已经非常成熟，其优化效果对图像处理整体速度的提高效果甚微。因此，提高图像处理速度的关键在于图像预处理过程的优化。

3 基于行程编码法的形态学膨胀优化算法

3.1 行程编码

行程编码用于描述图像核心区域。在一个逐行扫描处理的图像矩阵中，具有相同灰度值的像素序列为一个行程。该行程仅存储灰度值常数k与行程长度L，从而避免了同一的灰度值的反复存储。若n×n区域图像数据矩阵中第α行像素灰度值为(k0,k1,…,kn)，其中ki～ki+5为该行中一个像素集合，灰度值常数为k，则该行程编码表示为(k,6)。

由定义可将图像关注区域视为其全体行程编码的集合。由于行程编码表示区域具有同一灰度值，因此在对图像关注区域进行逻辑交、并运算过程中可避免大量的重复冗余计算[10]。

3.2 形态学膨胀与优化特性

在轨道视觉检测过程中由于光线的干扰经常会出现阈值分割处理后轨道轮廓的“断线”和“边缘毛刺”的现象。这严重影响了系统检测的精度。因此需要利用形态学膨胀的方法来使断线和毛刺重新“生长”成为一个平滑的连通区域。

形态学膨胀定义为：

其中M为关注区域ROI，N表示为结构元。

本系统通过独特的视角提醒人们关注日常居室环境，避免室内污染对身体健康在不被感知的情况下造成的损害。采用方便、简单的设计实现室内环境数据的采集和呈现，并通过共享到云服务器为环境大数据分析提供依据。同时也考虑后期维护上比较容易，成本低、效率高。

形态学膨胀可以视为在Minkowski 加法中使用转置的结构元得到的运算结果，其中Minkowski 加法可定义为[11]：

即当转置后的结构元与ROI 存在非空交集时则以当前覆盖区域为运算结果进行存储。由定义可知其满足交换律M⊕N=N⊕M与分配律(M∪N)⊕T=M⊕T∪N⊕T。这是基于行程编码优化的形态学膨胀算法成立的重要基础。

3.3 行程编码对膨胀过程的优化

若mi、nj分别为ROI 与结构元区域的单一行程的行程编码；a、b表示两个区域各自的行程数。则基于行程编码优化的形态学膨胀算法的具体优化过程如下：

将ROI 与结构元逐点求非空交集的形式转化为利用行程编码运算求解形式，如式（3）所示：

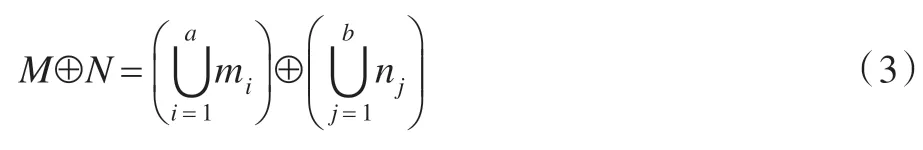
利用交换律与分配率进行转换如式（4）所示：

分别计算单一行程mi、nj的膨胀结果mi⊕nj，并对a、b次单行程处理结果求并集，优化后的Minkowski 加法可用行程编码方法表示为式（5）形式：

由于对单一行程求并集运算极其简单，通过算法的时间复杂度T(n)来对比算法优化前后的运算效率。

时间复杂度T记为：

随着n的增大，算法执行的时间增长率和函数ƒ(n)的增长率成正比[12]。若矩形图像与ROI 区域尺寸分别为U×U和u×u像素，则其行程数分别为U与u。其中结构元为一个直径为v像素的圆型区域，故其行程数为v。依据Minkowski 加法定义直接对二值图像进行膨胀处理的时间复杂度为O(U2v2)，而优化处理后的时间复杂度为O(uv)。由于U≫u故算法执行效率以2 阶提高，因此经算法优化后的形态学膨胀运算计算量明显降低。

综上，基于行程编码优化的形态学膨胀算法在时间复杂度上较二值图像直接进行膨胀处理有效降低。因此，可将其应用于对图像处理实时性要求极高的轨道视觉检测系统中。此外，在实际应用过程中，形态学膨胀并不能完全消除干扰，故前期还需对图像进行滤波去噪与图像灰度变换处理以降低光斑噪声对测量精度的影响，其具体算法与实现过程由于篇幅所限另文详述。

4 实验验证与数据分析

图2为轨道视觉检测系统提取的一副800×640的8 bit轨道图像。实验条件为：实验室环境下日光灯漫射照明。选用CCD 工业摄像机的像素尺寸为5.6 μm×5.6 μm，帧率60 f/s，信噪比>52 dB。图中白色亮带为一字线性激光光源垂直照射轨道形成的轮廓线，激光光源为红光，扇角10°，波长650 nm；实验选用图形处理器为Intel 至强X3450，工作站主频为2.66 GHz。

图2 轨道图像

实际应用中为降低阳光等外界光线干扰，采用最大类间方差自动阈值分割方法对光带信息进行动态提取，该方法可有效降低固定阈值法造成的图像信息丢失与冗余[13]，其选取的最优阈值即使该类间方差取最大值时的阈值[14]。该方法抗干扰能力强，尤其适用于分割目标与背景反差较大的图像分割应用[15]。本实验中图像分割结果如图3（a）所示。将二值图像局部放大可见存在断线和边缘毛刺现象，这一现象导致不能在进一步细化处理时得到准确的像素坐标，从而影响到测量精确度。

为了填补和平滑处理断线与边缘毛刺，需要对阈值分割后的二值图像进行形态学膨胀处理。实验采用基于行程编码的形态学膨胀优化算法对图像进行膨胀处理，处理结果如图3（b）所示。

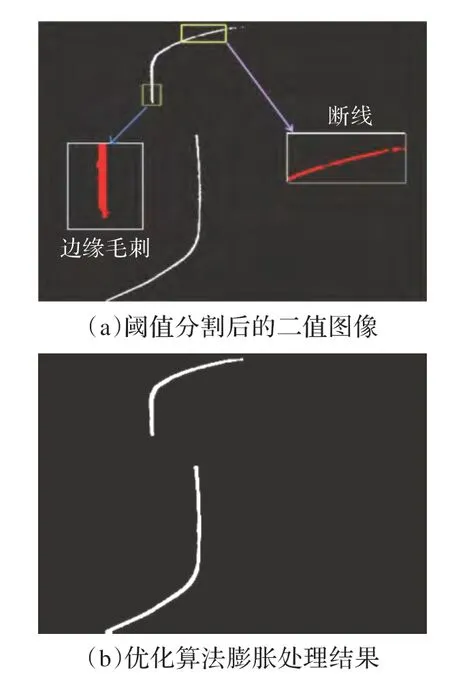
图3 优化算法处理前后比较

可见优化算法将断线和边缘毛刺完全消除，并得到平滑的轨道轮廓，形成一个完整的连通区域。由式（5）可知，优化算法并不会改变形态学膨胀的处理结果，仅在运算过程中进行了优化。

图4 为基于行程编码优化的形态学膨胀算法的处理流程与图像编码处理过程。

对优化前后10 帧图像处理时间进行分析，以进一步验证优化算法在处理实时性上的优势，统计结果如表1 所示。

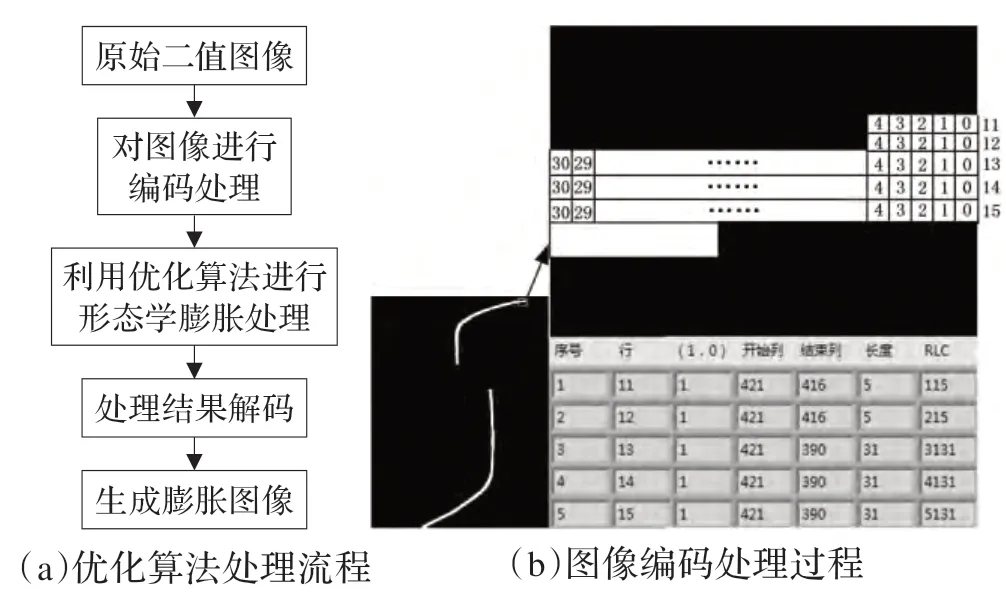
图4 优化算法处理流程与编码处理过程

表1 优化前后10 帧图像处理时间统计 ms

由表1 可见，基于行程编码优化的形态学膨胀算法在单帧图像处理速度上较优化前大幅提高。为进一步探究优化算法对不同像素大小图像的处理结果，实验选取100 帧与图3 相同场景的6 种不同像素大小图像分别进行处理，优化前后平均帧处理时间与图像像素大小关系如图5 所示。

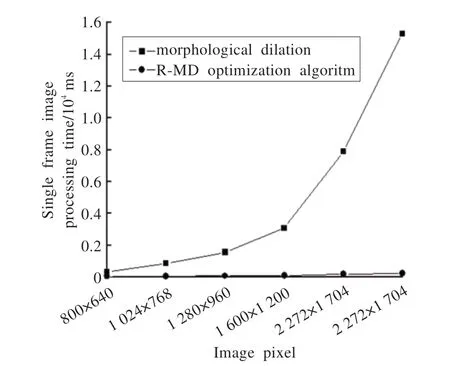
图5 不同像素图像优化前后帧平均处理时间

由图5 可见，对二值图像直接进行膨胀处理的帧平均处理时间随着图像像素的增大呈指数上升趋势，而优化后的处理结果随像素增大的上升趋势平缓。单帧图像处理速度完全能够满足轨道视觉检测系统实时在线高速检测的要求。

5 结束语

针对轨道轮廓图像阈值分割过程中存在边缘毛刺和断线现象，研究了基于行程编码优化的形态学膨胀算法并探究了其优化过程。将本文算法应用于轨道视觉检测系统的图像预处理过程中，依据优化算法特性与处理结果分析了优化前后轨道轮廓图像预处理速度差异。实验结果表明：（1）单帧图像经过基于行程编码优化的形态学膨胀算法处理的结果较阈值分割图像直接膨胀处理速度提高5 倍。（2）二值图像直接进行膨胀处理的图像帧处理时间随着图像像素的增长呈指数上升趋势，而优化处理后的帧平均处理时间上升趋势趋于平缓。（3）依据4 点/m 工务轨道检测规范，可提高理论检测精度到20 点/m 或在检测精度不变的条件下相应提高系统检测速度。

[1] Sonka M，Hlavac V，Boyle R.Image processing，analysis and machine vision[M].[S.l.]：Thomson-Engineering，2007.

[2] Kim W J，Kim S D，Kim K.Fast algorithms for binary dilation and erosion using run-length encoding[J].ETRI Journal，2005，27（6）：814-817.

[3] Trein J，Schwarzbacher A T，Hoppe B，et al.A hardware implementation of a run length encoding compression algorithm with parallel inputs[C]//Proceedings of Signals and Systems Conference（ISSC 2008），2008.

[4] 杨建中，王启富，黄正东，等.组合曲面的粗加工刀轨算法[J].计算机辅助设计与图形学学报，2006，18（2）：295-301.

[5] 吴铮，何明一.小波图像的膨胀-游程编码算法[J].电子与信息学报，2005，27（7）：1030-1034.

[6] 刘铁，任盛伟，许贵阳，等.GJ-4 型轨检车轨距-轨向检测系统改造[J].中国铁道科学，2006，27（6）：137-140.

[7] 许贵阳，史天运，任盛伟，等.基于计算机视觉的车载轨道巡检系统研制[J].中国铁道科学，2013（1）：139-144.

[8] 伏思华，于起峰，王明志，等.基于摄像测量原理的轨道几何参数测量系统[J].光学学报，2010（11）：3203-3208.

[9] Jin Wenrui，Zhan Xingqun，Jiang Benhe.An automatic scheme for rail wear detection based on infrared image analysis[C]//Proceedings of the 8th International Conference on Signal Processing，2006.

[10] 阮柏尧，陈伟峰，张歆奕.PCNN 与行程编码结合的图像压缩方法[J].计算机工程与应用，2008，44（20）：196-197.

[11] Steger C，Ulrich M，Wiedemann C.Machine vision algorithms and applications[M].[S.l.]：Wiley-VCH，2008.

[12] 王红梅，应红霞，季绍红.递归函数时间复杂度的分析[J].东北师大学报：自然科学版，2001（4）：111-113.

[13] 王昊.高速轨道检测图像处理技术[J].铁路技术创新，2012（1）：35-37.

[14] 李敏，罗洪艳，郑小林，等.一种改进的最大类间方差图像分割法[J].南京理工大学学报：自然科学版，2012，36（2）：332-337.

[15] 徐建东，孙迎春，李帅，等.基于多峰分布最大类间方差的垩白米粒检测方法[J].光电子·激光，2012（5）：956-960.