时间序列下模式挖掘模型设计

张可佳，李春生，姜海英，赵 森

ZHANG Kejia1,LI Chunsheng1,JIANG Haiying2,ZHAO Sen3

1.东北石油大学 现代教育技术中心，黑龙江 大庆163318

2.大庆油田有限责任公司 第二采油厂地质大队，黑龙江 大庆163000

3.大庆油田有限责任公司 矿区服务事业部，黑龙江 大庆163000

1.College of Computer and Information Technology,Northeast Petroleum University,Daqing,Heilongjiang 163318,China

2.The Second Oil Plant Geological Brigade,Daqing Oil Field Co.,Daqing,Heilongjiang 163000,China

3.Services Department,Daqing Oil Field Co.,Daqing,Heilongjiang 163000,China

1 引言

人工智能经过数十年发展，已经广泛应用于工业生产及工程施工的各领域，并发挥着极大的作用，如CNG-HSE 系统[1]、InterBay-System（IBS）[2]。由于信息化的普及，相关生产数据的完整性和准确性不断提高，伴随时间增长带来的数据量与日俱增，于是发现领域内数据内部规律，挖掘数据变化模式成为提高智能化应用准确度和有效性的关键[3]。时间序列的提出将关联关系以时间为维度建立，降低了大数据量分析过程中的数据间耦合度，突破数据关系分析的瓶颈，解决了模式挖掘过程中由数据关系带来的繁冗和高复杂度，使分布式并行计算的可用性和高效性更有意义。

领域决策者和专家的经验积累程度和较强业务能力对于智能化应用至关重要[4]。虽然通过知识工程的手段可以很好的发现业务领域内的影响因素变化规律和模式，较好地解决了相关领域内的故障认定、风险评价、措施优选等问题，但是依旧存在以下缺陷：（1）相比对于某种模式的描述，专家界定该模式涵盖的影响因子集合的准确程度更高，这将有利于模式挖掘中数据降维过程。现有多数方法过多的将专家定性化经验引入模式挖掘过程，增加了模式结果本身的不确定性因素，降低了模式挖掘结果的可靠性[5]。（2）多数模式挖掘结果的表达方式较为简单，应对复杂情况下的模式表达能力较弱。（3）由于缺乏对数据本身表象特征分析，忽略数值计算方法的作用导致有效数据项的拟合算法选取过于简单，在高阶拟合、余音处理等方面计算难度较大，响应时间过长，计算结果不够准确[6]。

针对此问题，设计时间序列下模式挖掘模型（TODM），提出FC 闭包模型表示由专家界定的原始影响因子集，以均方差收敛等方法清洗和过滤噪声因子。通过对数据离散点分布图进行分析，采用科学的分段拟合方法基于时间序列进行拟合，设计CCM-ECM 模型，实现对TODM 模型挖掘结果的量化特征描述，并提出一种置信度计算算法实现模型的校正和自适应过程，提高模式挖掘结果的高精细化描述程度，深度挖掘数据内部的潜在规律。

2 FC 闭包集的产生

专家组对于领域内与事务相关的影响因子界定较为准确，其判定的子集往往包含真实集[7]。将专家对于影响因子界定转化为抽象的逻辑表示形式是整个挖掘模型的基础。

2.1 原始影响因子集的获取

以n位专家组成的专家组，领域内存在某事务W，针对W发生后数据变化模式进行挖掘。取领域内影响因子全集R，分别由专家给出相应原始影响因子集，其表述形式为：

Efn={un1,un2,…,unp|u∈R}

其中Efn表示第n位专家的结果，u为全集R的元素，将专家的结果进行并运算，于是有原始影响因子集的一般表述形式为：Efa=Ef1∪Ef2∪…∪Efn。

2.2 FC 闭包模型的引入

为实现建立自然语言描述的影响因子与数据体内数据实体的映射关系，引入FC 闭包模型。具体定义如下：

定义1包含影响因子的自然语言形式u，直接描述u的数据实体df及映射关系函数F的闭包结构成为FC闭包。其一般表示形式为：

FC={u,df,F|df≠φ,u∈Efa}

其中，Efa为有专家组提供的原始影响因子集；df为数据实体，实例化后为数据体内的数据单项；F为映射关系函数，在u可直述时，F可为空，当u不可直述，df由F进行计算获得。

FC闭包模型建立自然语言与逻辑语言间的映射关系，并将因子间相互独立，可以清晰地描述其抽象结构，提高Efa集的松散度，易于分析和计算。

通过数据体模型获取Efa集元素的目标数据实体df，建立u与df间的映射关系F，结合数据集成思想，利用FC闭包模型表示形式，产生原始FC 闭包集FEfa，其一般表述形式为：

FEfa={FC1,FC2,…,FCn|n=len(Efa)}

FEfa集维度与Efa集维度相同，并存在一一对应关系，FEfa集将作为模式挖掘后续拟合计算的基础。

3 FEfa 集的有效化

受到专家不确定性经验及定性化知识影响，FEfa集往往包含真实集Tr，即Tr⊂FEfa。为了减少FEfa集内无效元素，提出一种时序下的数据处理和清洗方法，去除FEfa集内无效元素，降低模式维度，防止维灾。

3.1 分段时间序列下的数据处理

以FEfa集内元素FCn为例，在事务W发生后，给定时间序列T={t1,t2,…,tp}将FCn实例数据划分为p段等长数据，对tp={tp1,tp2,…,tps}内数据集合dp={dp1,dp2,…,dps}通过算法1 处理。

算法1

Begin：若dp原始数据长度s＞0

Step1：由公式（1）计算dp原始数据均值

Step2：将dp原始数据处理为局部距离数据

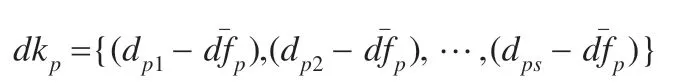
Step3：由公式（2）取局部距离的均方差

End

于是将FCn的数据处理为：

D={T,ϕ},T={t1,t2,…,tp},ϕ={ϕ1,ϕ2,…,ϕP}。

算法1只讨论二维情况，当然通过FC闭包模型可以较为容易的推广到多维情况。值得注意的是，算法1 中步骤2 中局部距离数据dkp将作为后续拟合过程中的真实数据样本，以此消除样本基数[8]差异带来的负面影响。

3.2 激巨变化和元素有效化判定

以经过处理后数据D={T,ϕ}为基础，根据切贝雪夫变形及均算术积函数[9]得到激巨判定函数如公式（3）所示：

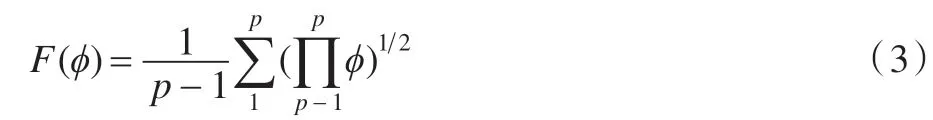
将函数还原得：

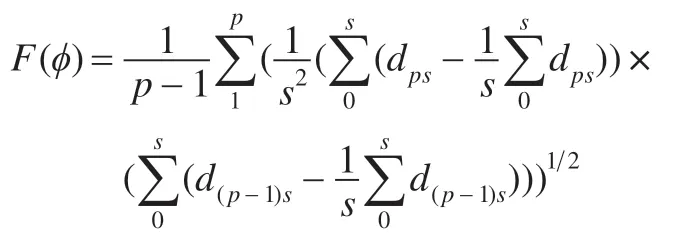
其中dps为分段内原始数据，s为分段内数据长度，p为分段量。

取μ(ϕ)=max(ϕ)-min(ϕ)，给出全局阈值系数ξ作为有效权重，于是得到阈值μr(ϕ)=ξμ(ϕ)，其中μr(ϕ)表示某元素的阈值。

根据激巨判定函数F(ϕ)，阈值函数μr(ϕ)，给出如下定义：

定义2在FEfa集内元素FCn内，以原始数据作为计算样本，当F(ϕ)＞μr(ϕ)，则认为FCn发生了激巨变化，且判定元素FCn是FEfa集的有效元素。

通过对FEfa集的搜索，逐一认定FCn的有效化，并去除无效元素，降低FEfa集的维度，并最终得到有效FEfa集（V-FEfa集，包含元素个数m）。在认定元素FCn有效后，将直接保留元素FCn的局部距离数据，并构成距离数据集合：

作为模式挖掘模型中FCn的数据样本。这种清洗和数据处理方式在降低维度的同时完成对时序拟合数据的预处理，降低后期时序拟合的复杂度。

4 时间序列下模式挖掘过程

数据体本身必定存在其内部复杂度不同的数学关系[10]。数据变化模式的最优计算方法是数值拟合进行参数计算，但对于最终表达形式的设计和拟合函数的选取一直是影响模式表示精准度的重要问题[11]。通过大量实验数据的处理，对其离散点分布图进行分析，采用一种相似度较高，拟合复杂度较低的分段拟合模型作为通用拟合方法，引入CCM-ECM 模型对最终表达形式分别描述，解决上述问题，完成模式挖掘。挖掘过程如图1所示。

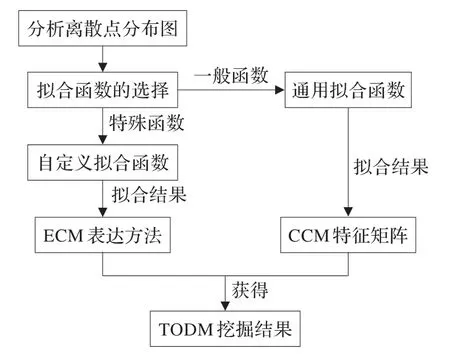
图1 TODM 模式挖掘流程图

4.1 P-L（普朗克-洛伦兹）模型的分段拟合

以工程施工或工业生产为例，当某重大行为（事务）W发生后，依据前述方法获取V-FEfa集及其各元素的距离数据集合作为样本，通过离散点分布图分析，得到如图2 所示。

图2 距离数据与时间序列（D-T）拟合曲线示意图

在事务W发生后，对于V-FEfa集某元素进行分析：在初始时间t0至最大效应时间tmax区间内，曲线呈激增上升状态，峰值为dkmax，在tmax至tps区间，曲线呈缓减下降状态，同时∀tϖ(w→p)，tϖ至tp区间作为函数余音。通过对高斯（Gaussian）、多项式、瑞利（Rayleigh）等多种模型进行分析匹配后，最终提出以P-L（普朗克-洛伦兹）模型进行分段拟合。普朗克（Planck）模型前期拟合准确度高[12]，适用于激增上升部分的拟合；洛伦兹（Lorenzian）模型对于样本量较大的拟合过程较为准确[13]，适用于缓减下降部分的拟合，同时洛伦兹模型处理余音的较强的鲁棒性，震颤情况较少。其他模型的优缺点分析在此不再累述。于是提出通用拟合方法的P-L模型表示形式，如公式（4）所示：

由拟合参数构成参数集Vr={a,b,c,d1,d2,d3,d4,τ}，并以{T,dk}进行拟合，逐一对满足P-L 模型元素FCm进行参数求解，得到：

Vrm={am,bm,cm,d1m,d2m,d3m,d4m,τm}

其中m是满足通用拟合模型的元素数量。对于不满足P-L 模型的元素可以进行单独分析结合业务或领域知识，选择适应其变化规律的独立拟合模型进行函数拟合，并得到其参数集Vgl，l为不满足通用拟合模型的元素数量，不同事务可以选取相应符合实际情况的通用拟合模型，具体过程不做累述。

4.2 CCM-ECM 模型的引入

在V-FEfa集各元素的拟合过程中，将元素序列依据是否满足通用拟合模型进行重新分类，并聚类抽象得到CCM-ECM 模型。具体定义如下：

定义3TODM 模型挖掘结果的表达方式（MOE）可由Vrm构成的特征矩阵CCM，及Vgl构成的余项集ECM表示，其一般形式如下所示：

其中余项集ECM={(F1,Vg1,1),(F2,Vg2,2),…,(Fl,Vgl,l)}，Fl为独立拟合模型或识别标识，Vgl为其参数集。由Vrm进行合并得到CCM特征矩阵：

通过CCM-ECM 模型实现的模式挖掘结果表示方式以数值计算方法为基础结合特征矩阵进行表示，屏蔽了外界因素的干扰和不确定性影响，单纯以数据角度反应与时间序列的关系，发现数据间的潜在规律，提供更准确的辅助决策支持。同时，这种设计思想对当下较为流行的大数据下的模式挖掘也具有较好的效果。

4.3 置信度校验

在获得TODM 模型结果后，需要对模型结果进行置信度校验，设定允许偏离最大误差率λ，以前述方法取得校验样本，并根据距离偏移误差公式得：

ψps=F(Tps)-dkps

其中ψps表示在某时间点Tps，预期结果F(Tps)与实际样本值dkps的偏移差，得到平均误差率的计算公式：

及最大误差率λmax的计算公式：

当λmax＜λ时，认为模型结果正确可信，当λ＜λmax,时，认为模型结果发生局部偏差，将进行局部重新拟合。当λ＜λmax,时，认为模型结果需要进行重新计算，模型将直接根据V-FEfa集进行取样，重复前述步骤，重新拟合计算并校正模型结果以实现自适应过程。

5 设计实例

以TODM 模型为基础，设计措施作业后模式挖掘模型，通过对油田施工后生产数据及相关作业历史数据进行分析计算挖掘油田生产过程中措施作业数据与油藏地质学相关的指标的变化规律和模式，应用在大庆油田某采油厂地质大队、作业大队等相关单位，为了缩小地质师和作业工程师的初次界定范围，规避客观环境影响，通过与油藏学家及上游生产信息系统（PCEDM）设计师的反复交流和推敲，对300 余项相关的指标（影响因子）进行筛选，遴选出40 余项具有典型变化特征和参照度极高的指标构成基础指标库（BER），如表1 所示。

表1 基础指标库信息表

表1 中指标可由现场专家根据施工作业及地质环境等实际情况提出疑义并讨论研究后进行增减，粒度程度表示指标的实际数据以时间为粒度的划分程度。

以强化采油（EOR）——酸化作业为例，为了提高效果的直观性，具体采用基质酸化作业为标准[14]。由6 位厂级地质师及4 位作业工程师组成的临时专家小组依据油藏数值、经验公式等知识对BER 分别筛选，并最后形成统一的原始指标集，其结构及组成如表2 所示。

表2 基质酸化的原始指标集(Efa)结构及组成

由于当前大庆地区主力油田处于高含水期和特高含水期[15]，原油含水量较高，出于保证实验结果的真实性的目的，降低环境及气候因素的影响，对于Z1 将进行去除产水量计算，即针对同一时间点取产油与产水量差值。同时，以已脱除地层水的萨尔图区块-萨二北浅层油层组初次完成基质酸化的16 口作业井进行取样，规定取样日期所处年月、季节及样本所处区块大致相同。将所有样本进行如下处理：

（1）以井为单位将数据分为16组样本，取样对象如表3所示，并随机取12组样本为训练样本，4组样本为校正样本。

表3 取样对象及相关属性表

（2）将所有训练样本以作业时间为准进行时间原点初始化，定义作业时间t=0。

（3）根据PCEDM 结构设计特点，根据指标与数据实体的关系进行原始数据采集，取生产日数据为指标的原始数据以提高实验的准确度，根据基质酸化作业的业务特点，取样范围为时间原点后900 日，并按30 日为周期将数据等长划分。

经过以上步骤完成对所有样本的原始数据采集和初步处理后，对样本原始数据进行有效化判定，最终将Z1-产油量、Z2-酸碱度、Z3-油压、Z11-壁粘稠度等7个元素判定有效，并计算相应的距离数据进行时序拟合。

有效元素经过数值匹配方法即可知Z1、Z2 等元素符合PL 模型，Z11 不符合PL 模型。图3 以Z1 及Z11 为例分别展示其离散点分布图。

图3 Z1 与Z11 离散点分布图

根据P-L 模型分段公式对符合通用模型的元素进行拟合并进行参数求解计算，参数计算结果构成的CCM矩阵特征矩阵为：

对于Z11 采用指数函数拟合模型进行拟合，构成的余项集

ECM={(Fdxs,Vg1Z11,1)},VglZ11={2,1.7,6}

以校正样本进行校正，根据专家意见，给出偏离最大误差率不高于5%，污染点个数小于5%进行校验，结果如表4 所示。

表4 校正样本误差率表

经过上述分析计算可知，最终得到基质酸化措施后的模式挖掘结果（ACI-MOE）误差精度不大于5%，同时可以发现非污染点数量越多，误差精度越小，所以TODM 对于数据准确率具有一定要求。

将上述ACI-MOE应用在另外20余口已酸化井进行同步数据监测，监测域为措施后3个月内PH值、产量等数据项，为节约篇幅，以PH值和产量为标准，同时应用模糊专家推理法（FS）进行比对，比对结果如表5 所示。

其中17 口井生产数据在开井后实际情况基本满足ACI-MOE 模式，N5-4-29X 井由于关停后转注，导致无明显变化从监测范围内排除，SN2-10-1 等2 口井发生数据大规模偏移，经作业大队检查，发现是由于抽油机故障和低温等问题发生了异常，由此可见，TODM 模型可以应用在故障排查、油田预警等领域。

根据TODM 模型开发的模式挖掘系统——井下作业跟踪监测评价系统已经正常工作，因为对数据内部潜在关系的深度挖掘和精确表达，较为广泛的应用范围和相对简单的应用过程受到了应用单位的较好评价。

6 结束语

提出了时间序列下的模式挖掘模型（TODM），以FC 闭包模型构建原始影响因子的形式语言表达结构，采用距离均方差算法以时间序列为基础将数据分段计算，根据数值计算方法及根据激巨变化函数实现对数据的预处理和有效化判定，同时根据数据特征和离散点分布图的分析给出科学合理的拟合模型；结合CCM-ECM模型实现对模式特征的抽象描述，并以距离偏移误差公式计算误差率进行置信度校验以验证结果的准确性，达到深度挖掘数据内部潜在规律，提高数据变化模式的高精细化描述程度的目的。

表5 应用效果比对表

[1] 郑言.我国天然气与安全评价与预警系统研究[D].北京：中国地质大学，2013.

[2] 吴立辉，颜丙生，张洁.求解全局优化问题的混合智能算法[J].计算机工程与应用，2006，42（16）：9-11.

[3] 刘立坤.海量文件系统元数据查询方法与技术[D].北京：清华大学，2011.

[4] Negnevitsky M.人工智能智能系统指南[M].北京：机械工业出版社，2012.

[5] 吴信东.带通配符和-条件的序列模式挖掘[J].软件学报，2013，24（8）：1804-1815.

[6] Deng Xiaoming，Wu Fuchao，Wu Yihong.An easy calibration method for central catadioptric cameras[J].Acta Automation Sinica，2007，33（8）：801-808.

[7] Lancichinetti A，Fortunato S.Consensus clustering in complex networks[J].Scientific Reports，2012，2：336-337.

[8] 杨一鸣，潘嵘，潘嘉林，等.时间序列分类问题的算法比较[J].计算机学报，2007，30（8）：1259-1265.

[9] 龙波涌.平均值与切贝雪夫泛函[D].长沙：湖南大学，2012.

[10] Liu W，Lv L.Link predicition based on local random walk[J].Europhysics Letters，2010，89（5）：58007.

[11] 尹文怡，范通让.离散数据拟合模型的研究与实现[J].计算机工程与应用，2008，44（31）：227-228

[12] 王虎，丁世飞.序列模式挖掘研究与发展[J].计算机科学，2009，36（12）：14-17.

[13] 陈家鼎，陈奇志.关于洛伦兹曲线和基尼系统的统计推断[J].应用数学学报，2011，34（3）：385-398.

[14] Yan L，Wang J.Extraction regular behaviors from social media networks[C]//Proc of the 3rd Int’l Conf on Multimedia Information Networking and Security，2011：613-617.

[15] 伍晓林，楚艳苹.大庆原油中酸性及含氮组分对界面张力的影响[J].石油学报，2013，29（4）：681-686.