标准模型下基于身份代理盲签名方案

陈 明

CHEN Ming

宜春学院 数学与计算机科学学院，江西 宜春336000

College of Mathematics and Computer Science,Yichun University,Yichun,Jiangxi 336000,China

1 引言

代理签名[1]（proxy signature）是原始签名者将自己的签名权限授予代理签名者，然后由代理签名者代表原始签名者实施签名的一种签名算法，在电子商务、电子政务和电子投标等领域有重要的研究和应用价值。

盲签名[2]（blind signature）是一种特殊的数字签名机制，签名者不知道他所签发文件的具体内容，且不能跟踪签名结果。也就是说，盲签名除了满足不可伪造性外，还需要实现盲性（blindness）[3]。盲签名被广泛应用于具有匿名性要求的领域（如电子支付和电子投票等）。结合代理签名和盲签名机制，Lin 等人[4]提出代理盲签名（Proxy Blind Signature，PBS）方案。代理盲签名方案在一些特定的场景下具有重要的应用价值，例如，由于时空限制，签名者不能亲自履行签名职责，同时兼具匿名性要求。最近，PBS 方案得到广泛的研究，主要分为基于证书的PBS[5]、基于身份的PBS[6-11]和基于无证书的PBS 方案[12-13]。

基于身份密码学（Identity-Based Cryptography，IBC）[14]是一种将用户身份标识（ID）作为用户公钥的非对称密码体制。在IBC 系统中，一个可信的密钥生成中心（Private-Key Generator，PKG）根据用户ID 使用其主密钥为用户生成长期私钥（不产生公钥证书，用户私钥与ID 相关）。IBC 算法中，系统直接将PKG 公钥和用户ID 作为算法输入，无需使用公钥证书，不仅降低了密码算法的计算开销和实现成本，而且去除了PKI 体制中的公钥证书管理负担。自Boneh 和Franklin 提出基于双线性对理论的身份基加密方案（IBE）[15]以来，这一密码体制得到广泛而深入的研究。

最近，结合IBC 与PBS，研究人员提出（IBPBS）方案。部分IBPBS 方案[6-10]基于Boneh 和Franklin 的IBE 机制，采用双线性对理论；其他IBPBS 方案[11]不采用双线性映射理论，基于椭圆曲线的离散对数问题（Discrete Logarithm Problem，DLP），以降低方案的计算开销。但是，上述研究成果要么没有提出明确的形式化安全模型，要么采用随机预言（Random Oracle，RO[16]）的可证明安全模型[11]。随机预言模型下可证明安全并不代表真实世界的安全，因为它依赖于现实世界无法实现的随机预言假设。基于标准安全模型（无随机预言）的IBPBS 方案还有待进一步研究。

2006 年，Paterson 等人[17]在欧洲密码会议上提出了一种基于身份签名方案（PS-IBS）及其标准安全模型。就目前掌握的资料来看，PS-IBS 方案是唯一一种在标准模型下可证明安全的IBS 方案，并且被其他研究者广泛研究，衍生出标准模型下的代理签名[18]和（部分）盲签名[19]等。基于PS-IBS 方案，本文构建了一种新的IBPBS 方案，并且基于Paterson 的标准安全模型[17]，结合代理签名的敌手模型[20-21]和盲签名的安全模型[22]，形式化定义了IBPBS 方案的标准安全模型。新的IBPBS 方案在标准模型下被证明满足不可伪造性和盲性。

2 背景知识

2.1 双线性映射与困难数学问题

这里简要描述双线性映射理论及困难数学问题和假设，详细内容请参考文献[17]。

双线性映射：给定大素数p，阶为p的循环群G1和G2，g是G1的一个生成元，如果e：G1×G1→G2是从G1到G2上一个有效的双线性映射，那么满足：

（1）双线性，给定u,v∈G1和任意的a,b∈ℤp，满足e(ua,vb)=e(u,v)ab；

（2）非退化性，e(g,g)≠1；

（3）可计算性，任意的u,v∈G1，存在多项式时间算法能成功计算e(u,v)。

CDH（Computational Diffie-Hellman）问题：对于任意未知的整数a,b∈ℤp，给定，求解gab。

CDH 假设：如果不存在多项式时间算法在时间t内以至少є的概率求解CDH 问题，那么称(є,t)-CDH 假设在G1上成立。

2.2 基于身份代理盲签名算法模型

基于身份的代理盲签名主要由6 个算法组成：系统建立（Setup）、用户私钥产生（KeyGen）、代理签名授权（Delegate）、代理签名密钥产生（ProxyKeyGen）、代理盲签名（ProxyBlindSign）和签名验证（Verify）。签名方案主要包含5 类用户：私钥生成中心PKG、原始签名者uo、代理签名者up和签名请求者U、签名验证者V。

Setup 算法由PKG 执行，功能是产生和发布系统公开参数params，生成PKG 的主密钥msk。

KeyGen 算法由PKG 执行，输入用户ID，PKG 利用其主密钥msk产生与用户ID 相关的私钥dID，并通过安全信道发送给用户。

Delegate 算法由原始签名者uo执行，输入代理授权书w，产生代理签名授权δ。

ProxyKeyGen 算法由代理签名者up执行，首先验证所收到的代理签名授权δ是否正确，如果正确则继续执行，产生代理签名密钥psk；若验证不正确，则重新请求代理授权。

ProxyBlindSign 算法是代理签名者up和请求签名用户U之间的交互协议，分为3 个步骤：第一步是盲化（Blinding），由用户U执行，选择随机参数对待签名消息m进行盲化处理，产生盲消息m′并发送给up；第二步是盲签名（BlindSign），由up执行，利用psk对盲消息m′进行签名，并将签名结果返回给U；第三步是去盲化（Unblinding），由用户U执行，产生最终的代理盲签名结果σ。

Verify 算法由验证者V执行，验证代理盲签名的正确性，输入，输出“T”表示接受代理盲签名，或者“⊥”表示拒绝。

2.3 基于身份代理盲签名安全模型

代理盲签名主要应满足：不可伪造性和盲性。

首先讨论签名不可伪造性（Existential Unforgeable against adaptively Chosen Message Attack，EUF-CMA[22]）。

代理签名方案主要包含3 类敌手[20，21]：第一类敌手AI只能访问公开参数；第二类敌手AII除可访问公开参数外，还可访问代理签名者的私钥；第三类敌手AIII除可访问公开参数外，还可访问原始签名者的私钥。可见，AII（和AIII）蕴含了AI敌手。也就是说，代理签名方案应该在AII和AIII敌手攻击下可证明安全。

基于Paterson 的标准签名模型[17]，本文定义敌手A∈(AII,AIII)与挑战者B之间的游戏（IBPBS-EUF-CMA Game）模拟IBPBS 方案的不可伪造性。

IBPBS-EUF-CMA Game

系统建立：B执行系统建立算法，输出系统公共参数params，并发送给A。

询问：A自适应地执行多项式时间有界（次）的询问。

-KeyGen 询问，A提交一个用户身份u，B返回其私钥du；

-ProxyBlindSign 询问，A提交原始签名者身份uo、代理者身份up和授权书w给B，由B模拟代理者up，A模拟签名请求者U，共同交互完成代理盲签名σ。

伪造：询问阶段结束后，A输出伪造代理盲签名。

（1）对于AII敌手：要求AII在询问阶段从未请求对的KeyGen 询问和对的ProxyBlindSign询问。

（2）对于AIII敌手：要求AIII在询问阶段从未请求对的KeyGen 询问以及对的Proxy-BlindSign 询问。

定义1如果不存在概率多项式时间算法A，在时间t内以至少є的概率赢得IBPBS-EUF-CMA 游戏，那么IBPBS 方 案 满 足(є,t,qe,qs) -IBPBS-EUF-CMA 安 全。这里，A最多执行了qe次KeyGen 询问和qs次Proxy-BlindSign 询问。

下面，讨论盲性[3，22]。盲性是指签名者不能将最终签名结果与具体签名实例相对应，不能实现对盲签名消息的跟踪。参考文献[22]，本文形式化地定义敌手A与挑战者B之间的游戏（IBPBS-Blindness Game）模拟IBPBS 方案的盲性。

IBPBS-Blindness Game

系统建立：B执行系统建立算法，输出系统公共参数params，并发送给A。

准备：A选择两个等长且可区分的消息m0和m1、原始签名者与代理签名者身份(uo,up)以及授权书w，提交给B。

挑战：B随机选择比特位b∈{0,1}，请求A分别执行对消息(mb,w)和(m1-b,w)的代理盲签名。随后，B执行去盲算法，并返回对(mb,w)的最终代理盲签名给A。

应答：A输出对b的猜测b′，如果等式b′=b成立，那么A赢得游戏。

A赢得IBPBS-Blindness游戏的优势定义为：

AdvIBPBS-Blindness(A)=|2Pr[b′=b]-1|

定义2如果不存在多项式时间敌手A以不可忽略的优势赢得IBPBS-Blindness游戏，则IBPBS机制满足盲性。

3 基于身份的代理盲签名

Setup输入安全参数k，输出公共参数params={G1,G2,e,g,g1,g2,Q,u′,U,w′,W,m′,M,H1,H2}。其中，e：G1×G1→G2是满足条件的双线性映射；g是G1的生成元；α∈ℤq和g2∈G1由PKG 随机选择，g1=gα,Q=e(g1,g2)是PKG 的公钥，是PKG 的主密钥；PKG随机选择u′，w′，m′∈G1和长度分别为nu，nw和nm的向量U=(ui)，W=(wi) 和M=(mi)，向量中的元素ui，wi，mi∈G1；选择抗碰撞的Hash函数H1：{0,1}*→{0,1}nw和H2：{0,1}*→{0,1}nm分别用于将授权书和待签名消息映射到大小为nw和nm的消息空间。这里要求用户的身份ID 统一为nu位二进制串。

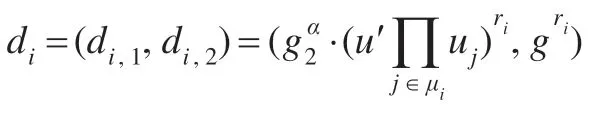
ProxyBlindSign用户U请求代理签名者up对消息m进行代理盲签名。

夏冰一边往后门走，一边回头看，不想踢翻了一个花盆，花盆掉进水池里，激起一股水花，一声闷响在静夜里格外刺耳。“谁？”夏冰听得身后方向传来一声询问，心里一惊，立即矮在树影里，紧握手枪，浑身冒汗。过了好一会儿，并不见人，才小心地站起来，四处打量。

输出对m的代理盲签名s=(s1,s2,s3,s4,s5,s6)。

Verify验证者V验证等式：

其中，mo、mp、ϖ、θ如前所述。若等式成立则接受签名；否则拒绝。

4 方案分析

4.1 正确性分析

本文方案的正确性由下列等式证明：

等式（1）表明用户私钥有效。

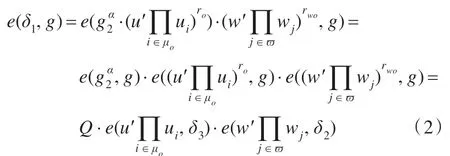
等式（2）表明代理签名授权与验证有效。

4.2 不可伪造性分析

证明假设存在(є,t,qe,qs)-forgerA，将构造一个算法B利用A，在时间t′内以至少є′的概率解决CDH问题。下面模拟B与A之间的游戏。

系统建立：B设置lu=2(qe+qs）和lm=2qs，随机选择整数ku，km和kw，满足条件：0 ≤ku≤nu、0 ≤km≤nm、0 ≤kw≤nw。对 于 给 定 的(qe,qs,nu,nm,nw)，假 设 有lu(nu+1)＜q、lm(nm+1)＜q、lw(nw+1)＜q。B随机选择整数x′←ℤlu，度为nu的向量X=(xi)，其中，X的每个元素xi满足xi←ℤlu。类似的，B构造参数z′←ℤlm和Z=(zj)，以及y′←ℤlw和Y=(yt)。随后，B随机选择s′,v′,d′←ℤp以及度为nu,nm,nw的向量S=(si)，V=(vj)和D=(dt)，分别满足si,vj,dt←ℤp。B定义三组函数如下：

这里，μ∈{1,2,…,nu}表示用户标识u中比特值等于1 的位置i的集合；θ∈{1,2,…,nm}表示H2(m) 中比特值等于1 的位置j的集合；ϖ⊆{1,2,…,nw}表示H1(w)中比特值等于1的位置t的集合。然后，B构建公共参数：

最后，B将公共参数{G1,G2,e,g,g1,g2,u′,U,w′,W,m′,M,H1,H2}发给A。这里，U=(ui)，M=(mj) 和W=(wt)，与文献[17]相同，存在下列等式：

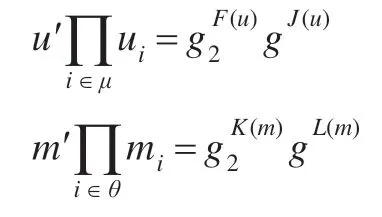
从A的视角来看，所有公共参数在空间上均匀分布。这里存在CDH 问题：。

询问：A自适应地执行多项式时间有界（次）的询问。

用户私钥满足下列等式：

-ProxyBlindSign 询问，A提交原始签名者身份uo、代理签名者身份up和授权书w，自己持有m。

如果F(uo)=0 modp∧T(ω)=0 modp，或者F(up)=0 modp∧T(ω)=0 modp，B终止游戏（其中ω=H1(w)）；

如果F(uo)≠0 modlu∧F(up)≠0 modlu，B首先执行KeyGen 询问计算do和dp，然后按照Delegate 算法和ProxyKeyGen 算法计算代理签名密钥；

如果F(uo)=0 modp∧T(ω)≠0 modlw，B不能计算do,1，按如下方式计算代理签名授权，首先随机选择ro∈ℤp和rwo∈ℤp，然后计算：

如果F(up)=0 modp∧T(ω)≠0 modlw，B不能计算dp,1，首先执行KeyGen 询问计算do，按如下方式计算代理签名密钥：随机选择rp∈ℤp和rwo∈ℤp，计算：

可以验证，psk=(psk1,psk2,psk3,psk4,psk5)是一个有效的代理签名密钥；

然后，由B模拟代理签名者up，A模拟签名请求者U，按照第3 章中的ProxyBlindSign 算法计算代理盲签名σ=(σ1,σ2,σ3,σ4,σ5,σ6)。

伪造：查询阶段结束以后，A输出原始签名者、代理签名者、授权书w*和消息m*的代理盲签名结果。这里，要求，并且，如果，那么A必然询问过的私钥。如果上述条件不满足，B终止游戏（其中ζ*=H2(m*)，ω*=H1(w*)）。

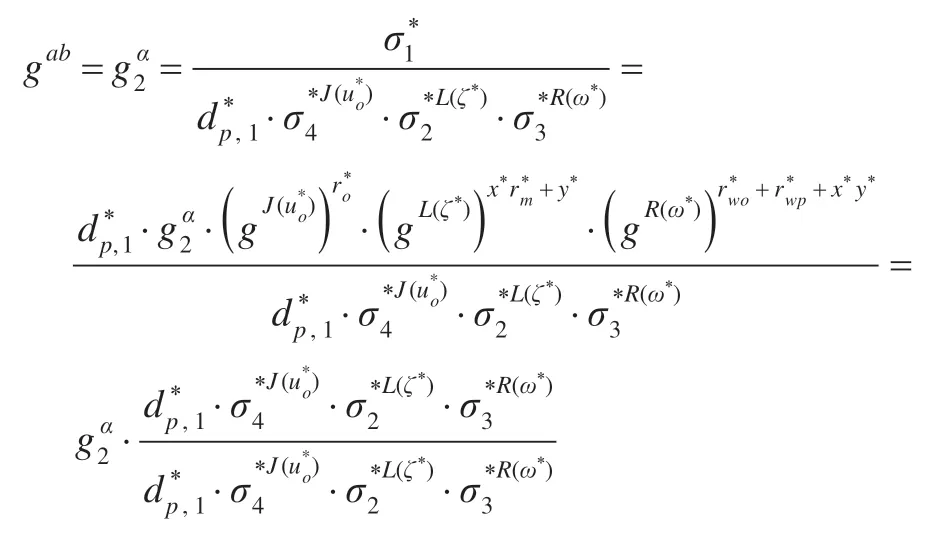
作为对CDH问题的回答。

作为对CDH 问题的回答。

游戏模拟到此结束，如果游戏没有终止，从以下几个方面分析B利用A求解CDH问题的概率。如果游戏没有终止，ProxyBlindSign 询问分为：（1）F(uo)≠0 modlu∧F(up)≠0 modlu；（2）F(uo)=0 modp∧T(ω)≠0 modlw；（3）F(up)=0 modp∧T(ω)≠0 modlw，3 个部分。

Ai F(ui)≠0 modlu

A*F(u*)=0 modp

Bj T(wj)≠0 modlw

B*T(w*)=0 modp C*K(m*)=0 modp

B没有终止游戏的概率为：

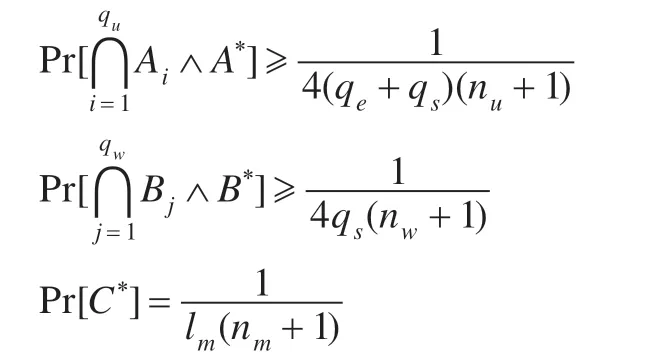
因此，如果游戏没有被终止，那么：

从算法的时间复杂度来看，在KeyGen 询问和ProxyBlindSign 询问中分别执行了O(nu)和O(2nu+nw)次乘法运算以及O(1)和O(1)次指数运算。令ρ和τ分别表示乘法运算和指数运算时间，那么算法B的时间复杂度为：

t′=t+O((qenu+qs(2nu+nw))ρ+(qe+qs)τ)

证毕。

4.3 盲性分析

定理2本文IBPBS 方案满足盲性。

证明本文采用与文献[22]类似的证明方案。设A是由代理签名者up控制的概率多项式时间算法，对于给定的(uo,up,mb,m1-b,w)、有效的代理盲签名(σ1,σ2,σ3,σ4,σ5,σ6)和签名发布中产生的中间结果（这里，b,i∈{0,1}），根据ProxyBlindSign 算法，有。考虑如下等式：

可见，盲因子(x,y)在代理盲签名的生成过程中总是存在且独立于A的视角，因此，A赢得IBPBS-Blindness游戏的优势是可忽略的。证毕。

5 结束语

基于Paterson 等人提出的标准模型下的身份签名方案，提出一种基于身份的代理盲签名方案。在Paterson的标准安全模型基础上，参考代理签名的敌手模型和盲签名的安全模型，本文形式化定义了基于身份代理盲签名的标准安全模型。通过安全模型的规约，本文方案被证明满足不可伪造性和盲性，具有可证明安全性。

[1] Mambo M，Usuda K，Okamoto E.Proxy signature for delegating signing operation[C]//Proc of the 3rd ACM Conf on Computer and Communications Security.New York：ACM Press，1996：48-57.

[2] Chaum D.Blind signatures for untraceable payments[C]//Proceeding of the Crypto’82，Plenum，NY，1982：199-203.

[3] Abe M，FujisakI E.How to date blind signatures[C]//Proceeding of the Cryptology-Aisa Crypt’96.Berlin Heidelberg：Springer-Verlag，1996：244-251.

[4] Lin W D，Jan J K.A security personal learning tools using a proxy blind signature scheme[C]//Proceedings of International Conference on Chinese Language Computing，Illinois，USA，2000：273-277.

[5] Lal S，Awasthi A K.Proxy blind signature scheme[J].Journal of Information Science and Engineering，2003，72.

[6] Dong Z，Zheng H，Chen K，et al.ID-based proxy blind signature[C]//Proceedings of the 18th International Conference on Advanced Information Networking and Applications（AINA 2004），2004，2：380-383.

[7] Lang W M，Yang Z K，Cheng W Q，et al.A new id-based proxy blind signature scheme[J].Wuhan University Journal of Natural Sciences，2005，10（3）：555-558.

[8] Yang M，Wang Y.A new efficient ID-based proxy blindsignature scheme[J].Journal of Electronics（China），2008，25（2）：226-231.

[9] Majhi B，Sahu D K，Subudhi R N.An efficient ID based proxy signature，proxy blind signature and proxy partial blind signature[C]//Proc Int Conf Information Technology（ICIT’08），LasVegas，NV，USA，2008：19-23.

[10] Yu Y，Zheng S，Yang Y.ID-based blind signature and proxy blind signature without trusted PKG[M]//Advances in Computer Science and Engineering.Berlin Heidelberg：Springer，2009：821-824.

[11] Tan Z.Efficient pairing-free provably secure identity- based proxy blind signature scheme[J].Security and Communication Networks，2013，6（5）：593-601.

[12] Zhang B，Xu Q.Certificateless proxy blind signature scheme from bilinear pairings[C]//Proceedings of the 2nd International Workshop on Knowledge Discovery and Data Mining（WKDD 2009），2009：573-576.

[13] 何滨，杜伟章.前向安全无证书代理盲签名方案的分析与改进[J].计算机工程与应用，2013，49（22）：104-109.

[14] Shamir A.Identity-based cryptosystems and signature schemes[C]//Proceedings of the CRYPTO 1984.Berlin Heidelberg：Springer，1985：47-53.

[15] Boneh D，Franklin M.Identity-based encryption from the weil pairing[C]//Proceedings of the CRYPTO 2001.Berlin Heidelberg：Springer，2001：213-229.

[16] Canetti R，Goldreich O，Halevi S.The random oracle methodology，revisited[J].Journal of the ACM（JACM），2004，51（4）：557-594.

[17] Paterson K G，Schuldt J C N.Efficient identity-based signatures secure in the standard model[C]//Proceeding of the Information Security and Privacy（ACISP 2006），Berlin Heidelberg：Springer-Verlag，2006：207-222.

[18] 谷科，贾维嘉，王四春，等.标准模型下的代理签名：构造模型与证明安全性[J].软件学报，2012，23（9）：2416-2429.

[19] 张延红，陈明.标准模型下增强的基于身份部分盲签名[J].四川大学学报：工程科学版，2014，46（1）：95-101.

[20] Huang X，Mu Y，Susilo W，Wu W.Proxy signature without random oracles[C]//Proc of MSN 2006，13-15 December，2006.Berlin Heidelberg：Springer，2006：473-484.

[21] Boldyreva A，Palacio A，Warinschi B.Secure proxy signature schemes for delegation of signing rights[J].Journal of Cryptology，2012，25（1）：57-115.

[22] Pointcheval D，Stern J.Security arguments for digital signatures and blind signatures[J].Journal of Cryptology，2000，13（3）：361-396.