基于距离区间概率测距的无线传感器网络定位算法研究

胡良梁

(重庆第二师范学院，重庆 400067)

1 概述

无线传感器网络具有自组织、分布式、多跳性等特性，能够实现传感数据的采集、传输及加工，目前在军事、农业及工业上有着广泛的应用。无线传感器网络由大量节点构成，其节点的位置信息至关重要。受规模及成本的限制，网络中大多数节点的位置信息未知，未知节点需要利用测距模型或逻辑跳距来测量相邻节点间的距离，再结合定位技术实现自身位置的获取。

测距技术根据测量原理可以分为物理测距和逻辑测距，物理测距是通过辅助设备来测量节点间的距离，逻辑测距是用跳数来表示节点间的距离。常用的物理测距技术包括三种：接收信号强度指示法(RSSI)[1]、基于到达时间的测距方法(TOA）[2]、到达时间差法(TDOA)[3]。RSSI（Received Signal Strength Indicator）是基于信号强度衰减的测距方法，通过模型将节点间信号衰减值转换成节点间距离，该方法不需要额外的硬件便可实现。通常RSSI测距模型是基于经验的测距模型，在实际应用中，信号受障碍物、反射、多径传播等影响，基于经验的测距模型中RSSI与距离映射存在多值问题，导致测距会存在较大的误差。本文利用基于距离区间概率的RSSI测距方法来消除多值问题，提高测距模型的测量精度，并减少定位算法的定位误差。

2 相关工作

2.1 基于经验的测距模型

大量的实验测试得出，信号强度衰减与距离存在一定的相关性。基于经验的测距模型如下：

其中Δ0为参考距离，一般取Δ0=1；P0表示节点离发射节点Δ0处的信号强度值；np为环境影响因子，其值依赖于部署的环境，一般取3～5；dkl表示相邻节点k，l之间的距离；Pkl表示相邻节点k，l之间的信号强度值。考虑到实际环境中信号传播会受环境、天气、障碍物等影响，在传播模型上引入服从正态分布的随机变量Xσ，如式(2)所示。

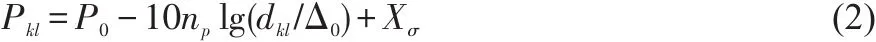
基于经验的测距模型简单实用，但在实际的传播过程中信号易受环境、天气、障碍物等影响，RSSI与距离d之间并非一一映射关系，会存在某一距离下存在多个RSSI值，因此基于经验的测距模型建立的＜RSSI，d＞的对应关系存在较大的误差。

2.2 基于距离区间概率的测距模型

为了解决基于经验的传播模型在实际应用中存在的多值问题，提高测距模型的测距精度，文献[4]提出了一种基于区间概率的测距模型。测距模型分两个阶段：(1)离线测量阶段；(2)在线测量阶段。

离线测量阶段通过实验建立起RSSI值与距离的映射＜Rk，Dk＞，其中Rk为实验测量中某个RSSI值，Dk是与之对应的距离值的集合，利用贝叶斯公式计算RSSI值为Rk时节点位于各个测量点的概率，将RSSI值与距离的映射＜Rk，Dk＞扩展为＜Rk，Dk＝{d1(Pk1)，d2(Pk2)，…，dn(Pkn)}＞，则最终得到RSSI值为Rk对应的映射距离可通过式（3）计算，并将Rk和d的映射关系存到映射关系数据库中。

在线测量阶段在某个位置上测量多个RSSI值，并将这些值与映射关系数据库中的能量值进行比较，取相等或者差值最小值的平均值作为移动节点的最终位置。

2.3 MDS-MAP定位算法[5]

设m维空间中有N个传感器节点，节点i的坐标xi=(xi1，xi2，…，xim),节点j的坐标xj=(xj1，xj2，…，xjm)，dij表示节点i与节点j之间的距离，则N个节点的距离矩阵为D，如式（4）所示。

对B进行奇异值分解为B=VΛVT的形式，其中Λ是矩阵B的特征值由大到小组成的对角线矩阵，V是特征值对应的特征向量组成的正交矩阵，取Λ前k个特征值构成Λk，取V前k个特征向量Vk，B可以表示成：

由式（5）和（6）可以得出k维空间坐标解：Xk=VkΛ1/2k，Xk为节点相对坐标，结合锚节点的坐标信息，可以将Xk转换成节点绝对坐标。

3 基于距离区间概率测距MDS-MAP定位算法

本文提出了一种改进的MDS-MAP定位算法，该算法利用基于距离区间概率测距方法消除传统测距模型中存在的多值问题。该算法包括如下步骤：（1）基于距离区间概率测距阶段；（2）距离矩阵D的建立；（3）对距离矩阵D采用MDSMAP方法求出各节点的绝对坐标。

第一阶段：基于距离区间概率测距

首先通过实验离线建立Rk和d的映射关系数据库。将节点通信半径R分成若干等分，在每个距离点上收集n个RSSI值，根据式（3），建立Rk和d的映射关系数据库。网络部署并初始化完成后，节点根据在线测量方法，将接收到的RSSI转化成节点间的最终距离。

第二阶段：对邻居节点的距离矩阵D'利用最短路径算法求出任意两个节点之间的距离，建立距离矩阵D。

第三阶段：对第二阶段中建立的距离矩阵D利用MDSMAP方法，获得k维网络的相对坐标系统，一般取k=2或k=3，结合锚节点坐标信息，将相对坐标系统转化成绝对坐标系统。

4 算法仿真验证

算法仿真是在MATLAB环境下进行。如图1所示，250个节点随机部署在一个100m*100m的方形区域里，其中含有5个锚节点，节点通信半径为R=15m,锚节点用*来表示，未知节点用小圆圈来表示。定位算法性能用平均定位误差来评价，其定义为未知节点真实坐标到估计坐标的欧氏距离与通信半径的比值。假设未知节点经定位后的估计坐标为(xe，ye)，其真实坐标为(xt，yt)，则单个节点定位误差为平均定位误差（其中(n-m)表示未定位节点的个数）。改进的MDS-MAP定位算法测距环节中的离线实验阶段，将节点通信半径为R分成30等分，并在每个距离点上采集100个RSSI。图2给出了改进的MDS-MAP定位算法与基于经验的传播模型（np=4）的MDS-MAP定位算法在不同通信半径下的对比分析图，从图中可以得出在不同的通信半径下，本文提出的改进算法的定位精度均优于基于经验的传播模型MDS-MAP算法。

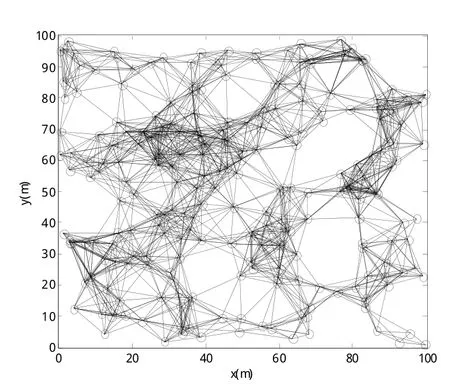
图1 方形区域邻居关系图

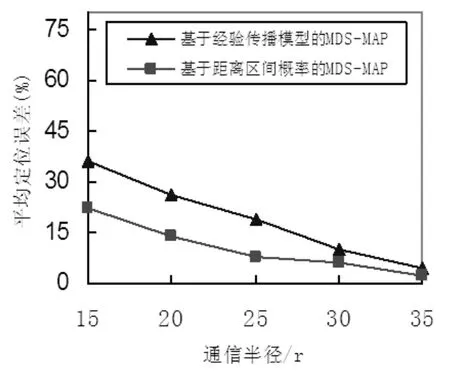
图2 不同通信半径下定位误差对比分析图

5 结论

传统的MDS-MAP算法在测距阶段当信号存在干扰或障碍物时，节点间的RSSI值与距离d存在多值问题，导致基于经验传播模型存在较大的测距误差。本文提出了一种改进的MDS-MAP定位算法，在测距阶段利用基于距离区间概率测距，消除RSSI值与距离d存在多值问题，提高了测距模型的抗干扰能力。改进算法提高了RSSI测量值的精度，进而提高了定位算法的精度。

[1]Bahl Paramvir,Padmanabhan Venkata N.RADAR:an inbuilding RF-based user Location and tracking system[A].Proceedings-IEEE INFOCOM[C],Tel Aviv,Isr,2000:775-784.

[2]L.Girod and D.estrin.Robust range estimation using acoustic and multimodal sensing[A].IEEE International Conference on Intelligent Robots and Systems[C],Maui,Hl,United states,2001:1312-1320.

[3]X.Cheng,T.A,G.Xue,D.Chen.TPS:A time-based Positioning scheme for outdoor Wireless sensor networks[A].Proceedings-IEEE INFOCOM[C],HongKong,China,2004:2685-2696.

[4]王媛媛,官娜娜.基于距离区间概率加权的RSSI测距方法[J].电子科技大学学报,2013.6（42）：862-868.

[5]Shang Y，Ruml W，Zhang Y.Localization from connectivity in sensor networks[J].IEEE Transactions on Parallel and Distributed Systems，2004，15（11）：961-974.