C-172R前起减震支柱密封圈寿命分布模型的研究

， 　

(1.中国民航飞行学院 航空工程学院, 四川 广汉　618307； 2.中国民航飞行学院 飞机修理厂, 四川 广汉　618307)

引言

Cessna172R型飞机作为最成功的轻型飞机之一，在全球范围内广泛使用。自2006年以来，某飞行学院共引进102架Cessna172R型飞机作为飞行员培训的初级教练机，但前起落架减震支柱漏油故障一直困扰着该机型。仅2007～2009年三年期间,该院172R型飞机共发生63次前起落架减震支柱渗油故障[1]。失效分析表明，减震支柱O形密封圈的扭曲损伤和断裂是导致该类型事故的主要原因，且数量呈上升趋势。因此，研究该部件的失效原理以及利用历史失效数据进行可靠性分析，确定寿命分布模型，不仅有助于提高该机型的安全水平，而且为合理制定维修计划、减少维护费用提供重要理论依据。

1　减震支柱O形密封圈的失效原理

172R型飞机前起落架减震支柱由内部装有混合油气的上、下支柱组成。上、下两支柱之间有一密封支撑环。减震支柱受外力作用时，密封支撑环和上部缸筒一起与下部缸筒产生相对运动，运动过程中动能与弹性势能相互转化，同时伴随摩擦转化为热能的消耗过程[2]。而整个运动过程中最容易出问题的地方是密封支撑环内的O形胶圈(如图1所示)。

Cessna172R型飞机前起落架减震支柱O形密封圈的失效主要是弹性变形失效和疲劳断裂失效。飞机在着陆或地面遇到颠簸时，减震支柱上、下缸筒产生相对运动，O形密封圈在该过程中主要受摩擦力。正常情况下，O形密封圈工作时应该在其外沿部位与缸筒的接触，因此密封圈的受摩擦位置也应该在其最大外沿处[3]。密封圈由于摩擦导致与缸筒接触的侧面出现微裂纹，该微裂纹在应力作用下导致应力集中，使零件局部应力大于平均应力，裂纹尖端的局部应力可能大于材料的强度极限，使裂纹不断扩大，而扩大化的裂纹将使局部应力现象更为严重。

图1　减震支柱结构图

并且减震支柱缸筒之间含有的液压油与高压氮气，对O形橡胶密封圈具有腐蚀作用。观察发现，密封在靠近化学浸蚀的一侧腐蚀情况严重，而靠近大气一侧的腐蚀较小[3]。摩擦应力作用下O形密封圈产生轻微裂纹，裂纹内液压油的pH值小于7，且随裂纹深度的增加而pH值越小。在该酸性环境下，丁腈橡胶的腐蚀速度加剧，同时裂纹在外部集中应力及腐蚀产物作用下加速了裂纹的扩张。这种在应力与腐蚀协同作用下导致零件结构破坏的现象称为应力腐蚀[4]。在应力腐蚀作用下，O形密封圈的破坏速度比两种因素单独作用时的破坏速度要快的多，最终导致O形密封圈的断裂失效。

以上从力学及化学角度对O形密封圈的失效做了简要分析，O形密封圈的损坏将导致漏油，致使减震支柱压力减小从而不能起到缓冲减震的作用。

2　非参数寿命分布估计与检验

Kolmogorov-Smirnov(K-S)检验，亦称D检验法，是一种非参数拟合优度(GOF)检验法。K-S单样本检验主要用来检验一组样本数据的实际分布是否与某一指定的理论分布相符合。它较χ2拟合优度检验法更为精确，还适用于小样本的情况[5]。

由于减震支柱O形密封圈寿命分布未知，因此根据该部件2007～2009年失效时间数据(见表1)，使用K-S非参数法进行分布模型的检验。

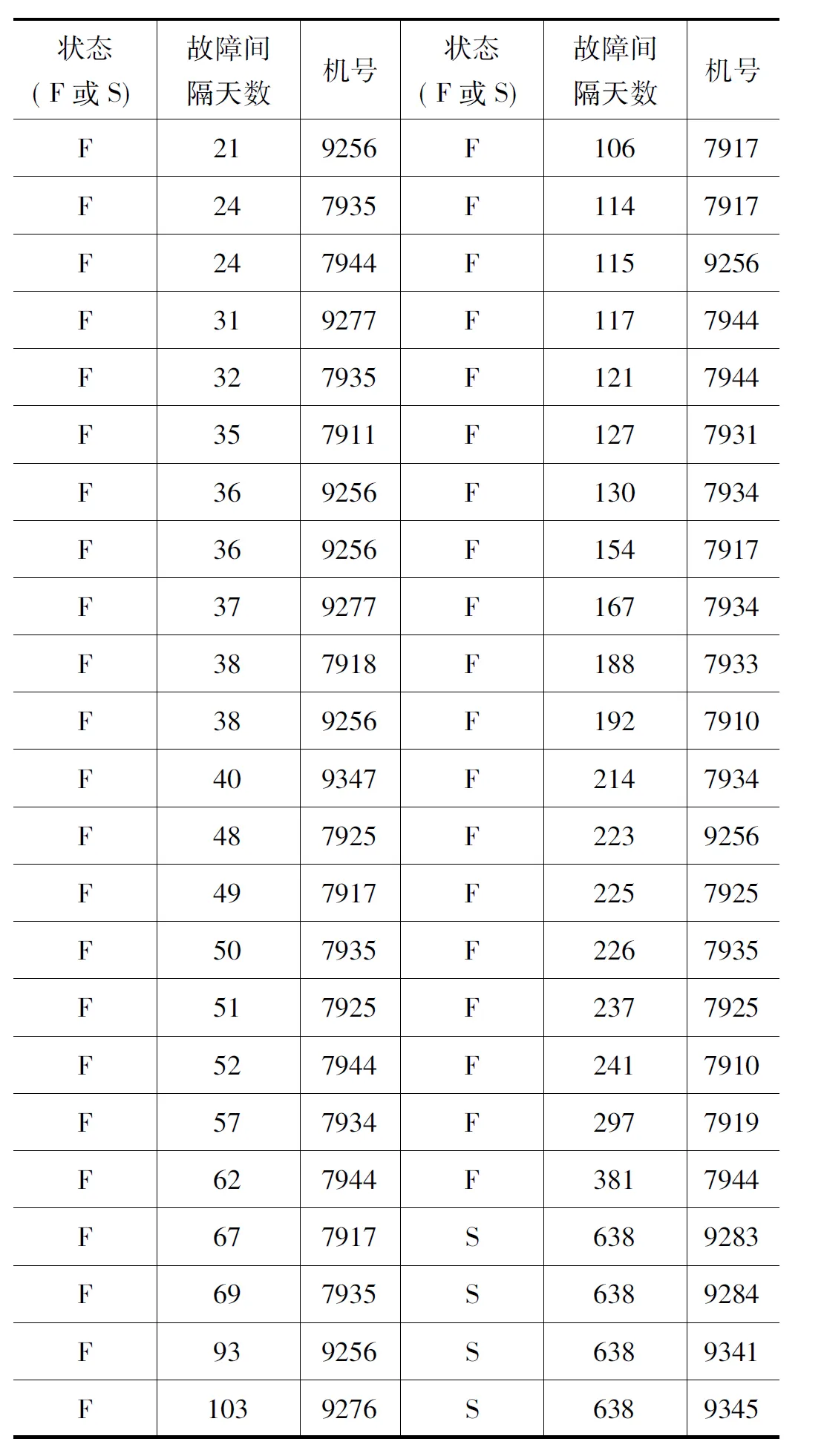
表1　失效时间统计表

注：F——失效；S——未失效截尾

D=maxFn(t)-F0(t)

(1)

式中，Fn(t)为一组随机样本的经验分布函数；F0(t)表示假设分布函数；D为两者绝对差的最大值。

根据样本容量n和显著水平α，查出临界值DC。将DC小于D的概率定义为拟合度，其值越大拟合效果越差。

本研究使用Weibull++软件进行分布平均拟合度的估计(见表2)及分布特征参数的求解(Weibull++是一款可靠性和寿命数据分析的专业软件，它提供了一系列标准的寿命数据分析、绘图和报表工具，并支持多种衍生应用分析[6])。

表2　平均拟合度计算结果

通过以上分析，该飞行学校C-172R飞机减震支柱O形密封圈失效数据更符合广义伽玛分布。

3　广义伽玛分布

广义伽玛分布最早由E.W.stacy于1962年提出，在可靠性理论、生存数据分析等领域得到广泛应用。作为一个灵活性很强的分布，可以用于拟合分布模型与参数未知的情况。随着参数取值的不同，广义伽玛分布为常见分布的特例(如威布尔分布、伽玛分布、对数正态分布、指数分布等)[7]，如图2所示。

图2　概率密度函数

广义伽玛函数为三参数分布，通常广义伽玛分布采用的参数为k、β和θ，此时广义伽玛分布的概率密度函数为：

(2)

其中θ>0为尺度参数，β>0和k>0为形状参数，Γ(x)为关于x的伽马函数，其定义式为:

(3)

该形式下，原始样本数据的数目的多少严重限制了其应用。即便是一个包含有200个数据或是更多样本点的样本，在最大似然估计方法下其结果也可能无法收敛。为克服该缺点将参数k、β及θ重新参数化，结果如下：

(4)

其中μ尺度参数，-∞<μ<∞；σ和λ为形状参数，σ>0，λ>0。虽然该转换简化了分布集中方面的运算，但是并未使人工处理方程过程变的简便。在允许λ取负值的情况下，以上概率密度函数变为：

(5)

该形式下广义伽玛分布的可靠性函数为：

(6)

(7)

根据可靠性基础理论，失效率函数：

(8)

由于该函数表达式过于复杂，本研究不予列出。

广义伽玛分布的可靠寿命函数TR的表达式为：

(9)

4　分布模型的参数估计

利用Weibull++对广义伽玛分布的相关参数进行求解，进而对零件的可靠性寿命作出预测。

寿命分布参数估计方法包括：概率图估计，在x轴的秩回归(RRX),在y轴的秩回归(RRY) 和极大似然估计(MLE)[8]。本研究选择最大似然估计法(MLE)进行分布参数估计，计算结果如表3及图3所示。

表3　分布参数估计

图3　似然函数剖面图

将表3特征参数计算结果带入式(5)～(9),得到：概率密度函数(见图4)。

图4　概率密度函数图

可靠性函数(见图5)。

R(t)=ΓΙ(0.35e-2.38ln(t)+9.26;0.35)

(11)

失效率函数：

图5　可靠性函数图

可靠寿命函数：

(13)

产品平均故障前工作时间(MTTF)是指产品发生63.2%不良时之预期时间，或称信赖度36.8%之时间。

t(R=0.368)=58.31天

基于安全寿命的维修时间间隔，是按照历史失效数据所确定的平均故障前工作时间除以分散系数得到的，即：

天

式中，TC为安全寿命，即维修时间间隔；MTTF为平均故障前工作时间；nf分散系数,一般取1.5。

因此，为提高提高飞行安全可靠性水平、降低事故发生的概率，建议将该零件的更换时间修改为35天。

5　结论

起落架系统的可靠性直接关系到飞机整机的可靠性水平，通过前起落架减震支柱O形密封圈寿命分布模型的研究，以及概率密度函数f(t)、可靠寿命函数TR、安全寿命TC等重要可靠性指标的确定，对O形密封圈设计改进和预防性维修检查时间间隔的确定都有重要意义。

参考文献：

[1]陈梁.对172R型飞机前起落架减震支柱故障的研究[J].科技信息,2011,(13): 506-507,467.

[2]罗裕富.Cessna172R型飞机前起落架原理及故障分析[J].中国高新技术企业, 2013,(10):52-53.

[3]夏祥泰,王志宏,刘国光,等.飞机起落架作动筒密封圈失效分析[J].失效分析与预防,2007,2(4):35-39.

[4]李向欣,孙立,那桂兰.关于金属应力腐蚀问题的分析[J].中国氯碱, 2004,(3):33-35.

[5]贺国芳,许海宝.可靠性数据的收集与分析[M]. 北京: 国防工业出版社, 1995.

[6]ReliaSoft Corporation. Weibull++培训手册[EB/OL].www.reliasoft.cn/products/papers.htm, 2014-06-23.

[7]E W Stacy. A Generalized of the Gamma Distribution [J].Annals of Mathematical Statistics,1962,(33):1187-1192.

[8]陈一鸣,黄安贻,李刚炎.气缸可靠性试验的数据处理[J].液压与气动,2009, (9):83-85.