高等数学教学中创新思维的培养

杨海霞

（兰州文理学院师范学院，甘肃 兰州 730000)

0 引言

高等数学是理工类的大学生必修的基础课,也是学习其他课程的一门工具,它扮演着越来越重要的角色.但大部分学生认为高等数学抽象乏味、枯燥难学,学习的主动性不高.为了搞好高等数学的教学,进一步激发学生的学习兴趣,教学不但应该传授数学知识,尤其要结合教学内容,适时地培养学生的创新思维和创造精神,提高高等数学教学的趣味性,思想性,培养学习的主动性,让数学学习变得简单起来.本文将结合高数数学的有关内容,从五个方面阐述如何在教学中培养学生的创新思维.

1 归纳思维

在高等数学中,许多重要结果的得出,都可以用到归纳思维,通过这些内容的学习和体验,可以逐步培养渗透学生的归纳思维.

例1 求某一函数的高阶导数时,通常的是求出其一阶、二阶（有时还要求出其三阶、四阶）导数,再归纳出n阶导数的表达式.

如：求余弦函数y==cosx的n阶导数.

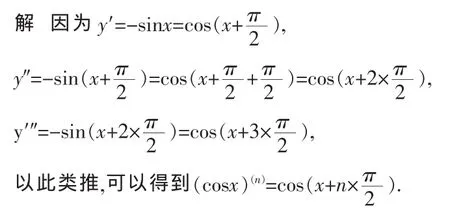
例 2 由两个可导函数的求导法则 （uv）′＝u′v＋uv′可归纳出任意有限个函数之积的法则.如:（u1u2…un）′＝u1′u2u3…un＋u1u2′u3…un＋…＋u1u2…un－1un′.

从一阶、二阶常系数线性齐次微分方程通解的结构及其求解方法,可以归纳出n阶常系数线性齐次方程通解的结构及其求解方法[1];多元函数求条件极值的拉格朗日乘数法,从两个自变量、一个约束条件,推广到n个自变量、m个约束条件,也是用归纳的方法得出的[2-3].著名的哥德巴赫猜想,费马猜想,素数定理等[4-5]都是通过大量观察、计算……,然后归纳得到的.

2 类比思维

类比就是由此去发现彼（或由彼去发现此）.在教学过程中,将新内容与已经熟悉的知识进行类比讲解,不但使学生易于接受、理解、掌握新知识,更重要的是可以培养、锻炼学生的类比思维,有利于开发他们的创造力.

例3 牛顿二项式展开公式和莱布尼茨公式的类比学习

这些公式比较繁琐,单纯记忆起来不方便,但通过将两个公式类比,发现将第一个公式中u＋v换成uv,将n次幂换成n阶导数(零阶导数理解为函数本身),就成了第二个公式,就易于理解和记忆.

例4 立体几何问题与平面几何问题的类比学习

在学习多元函数的微积分学时,应与已经学习过的一元函数的微积分相应的概念、理论、方法进行类比学习.

在学完了积分学后应将定积分、二重积分、三重积分、曲线积分、曲面积分进行类比,包括它们的定义、性质、计算方法、物理意义等等.通过类比学习，可以达到事半功倍的教学效果.

3 发散思维

在高等数学教学中,通过多种思路培养、训练学生的更广阔的思维,将所学知识能够活学活用,进一步开拓知识视野,提高解决问题的能力.

3.1 一题多解

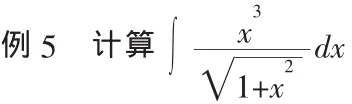
等等.

这道题目的计算过程中,使用了多种计算不定积分的方法,可以引导学生将所学知识活学活用,让同学们明白绝对不能以为获得一种方法以后,作业就完成了,问题就解决了,或把另外的解法当作浪费自己的时间.

（可以用洛必达法则;用等价无穷小的替换定理;用重要的极限；用三角公式变形；等等.）

3.2 一题多变

例7 求微分方程x2dx＝y2dx＋2xydy的通解

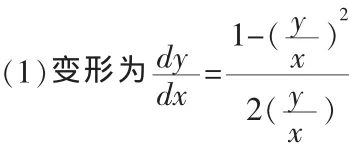
它是齐次微分方程,用齐次微分方程的解法求出其通解；

（2）变形为（x2－y2）dx－2xydy=0

所以它是全微分方程,可用全微分方程的解法求出其通解；

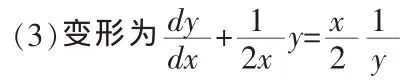
它就是伯努利方程,设z＝y2先化为线性微分方程,然后用线性微分方程的解法求出其通解[6].

4 逆向思维

是从已有的思路的反方向去思考问题.在高数的教学过程中,应渗透这种思维的培养,它可以开阔解决某些难题的思路,对解放思想、发现新生事物、开辟新的方向,往往能起到柳暗花明又一村的作用,可以更加激发学习数学的兴趣.

4.1 若遇到某些问题顺推不行,可以考虑逆推

例 8 求方程 ydx＋（x－lny）dy=0 的通解

解 利用逆向思维,将y视为自变量,x视为因变量 ,解题过程就会变得很容易.方程化为如下的线性方程：

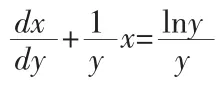
利用线性微分方程的通解公式很容易求出其通解

4.2 若遇到某些问题直接解决困难,想法间接解决

例10 将y=ln（1+x）展成x的幂级数.

解 若用直接展开法将函数展开成幂级数,展开过程中计算f（n）（x）的工作量大,还得讨论余项Rn（x）.间接方法,就变得很简便

5 合理的猜想

大科学家牛顿曾经说过：“没有大胆的猜想,就作不出大胆的发现.”纵观数学发展史,可以说,没有猜想就没有数学,更没有数学的发展.例如,著名的哥德巴赫猜想,费马猜想等.因此,在数学教学中应结合教材重视培养学生数学猜想的能力.

例如,在学习复合函数的求导法则时,利用已经学过的导数的含义（变化率）,引导学生合理的猜想出复合函数的求导法则.

例 11 若 y=f（u）,u＝φ（x）都是可导函数,求

通过大胆的猜想会给学生带来发现和成功的喜悦,不但可以牢牢记住这些内容,也逐渐提高数学猜想的能力,激发学习数学猜想的乐趣.

总之,在高等数学教学中渗透创新思维的培养,帮助学生在学习、研究、应用数学的过程中让数学变得活起来,更加深刻理解数学的内容、思想、方法及其应用,增强学习数学的热情,从而提高教学效果,逐步培养学生运用所学知识分析问题和解决问题的能力.著名教育家苏霍姆林斯基说：“思维就像一棵花,它是逐渐地积累生命汁液的,只要我们用这种汁液浇灌它的根,让它受到阳光照射,它的花朵就会绽开.”在数学教学中,创新思维必不可少.S

［1］同济大学应用数学系.高等数学[M].5版.北京:高等教育出版社,2004.

［2］华东师范大学数学系.数学分析[M].3版.北京:高等教育出版社,2001.

［3］刘玉琏.数学分析[M].2版.北京:高等教育出版社,1994.

［4］王树禾.数学思想史[M].北京:国防工业出版社,2003.

［5］朱家生.数学史[M].北京:高等教育出版社,2004.

［6］李心灿,等.高等数学一题多解200例选编[M].北京:机械工业出版社,2002.