一类未知参数的分数阶混沌系统投影同步的2种证明

孔德富，赵小山（天津职业技术师范大学理学院，天津　300222）

一类未知参数的分数阶混沌系统投影同步的2种证明

孔德富，赵小山
（天津职业技术师范大学理学院，天津300222）

摘要：基于分数阶稳定性理论，设计了一类普适的投影同步控制器与参数辨识规则，利用Lyapunov稳定性理论和J函数准则2种方法给予严格证明。数值仿真验证了该方法的有效性和正确性。

关键词：分数阶混沌系统；投影同步；参数识别

分数阶微积分与整数阶微积分几乎有相同的发展历史，但是近十几年来才成为国际上研究的热点。自1990年，Pecora和Carroll[1]首先提出了驱动-响应同步方法实现混沌同步以来，学者们定义了不同的混沌同步形式，如广义同步、完全同步、投影同步、延迟同步等[2-5]，并且提出了多种混沌同步方法，如滑膜控制、非线性控制、自适应控制等[6-8]。本文基于分数阶稳定性理论[9]，设计了投影同步控制器和参数辨识规则，并利用Lyapunov稳定性理论[10]和J函数准则[11-12]2种方法给予证明。

1　问题描述

考虑一个分数阶混沌系统为驱动系统，表示为如下形式：

对应的响应系统为：

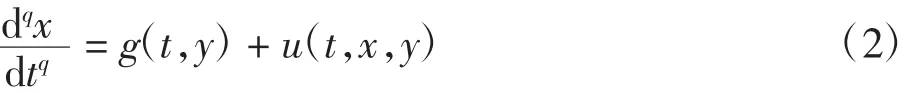
式中：x=（x1，x2，…，xn）T∈Rn，y=（y1，y2，…，yn）T∈Rn为相应的状态变量；u（t，x，y）为合适的控制器；0＜q＜1。由于系统的参数是不确定的，假设δ为系统中不确定参数的待估计值，δ为系统中不确定参数的真实值，则系统中不确定参数的估计误差为：

驱动系统（1）和相应系统（2）定义同步误差为：

式中：e=（e1，e2，…，en）T；ei=yi-αx（ii=1，2，…，n）；α称为比例因子。存在一个常数α（α≠0）使得：lim‖y -

t→∞αx‖=lim‖e‖=0，则称驱动系统（1）和响应系统（2）

t→∞之间实现了投影同步。

2　不确定的混沌系统投影同步与参数识别

定理1[9]对于非线性分数阶系统

式中：0＜q＜1；x=（x1，x2，…，xn）T为状态向量；A（x）∈Rn×n是系数矩阵。当含有状态变量的系数矩阵A（x）的所有特征值λi（i=1，2，…，n）实部都不大于零，即│arg（λi）│＞qπ/2时，系统（5）渐近稳定。

根据定理1，设计如下混沌系统投影同步与参数辨识规则。

文献[13]构造了一个具有3个非线性二次项的分数阶混沌系统，并将该系统作为驱动系统表示成如下形式：

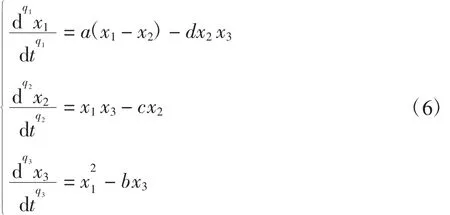
选取参数a=10、b=3、c=17、d=8，并且令q1=q2=q3=0.9，系统（6）存在混沌吸引子。如图1所示，可以清晰地看出该系统的运行轨迹为大小不等的2个双涡旋结构。

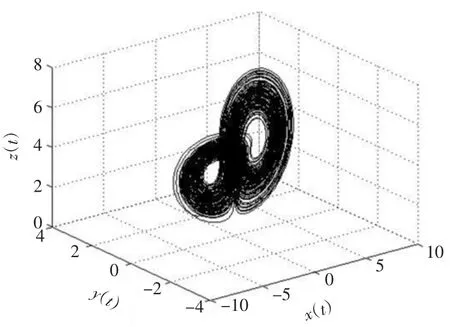
图1　系统（6）在x-y-z平面的吸引子

该系统所对应的响应系统为：

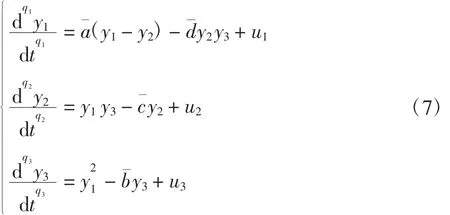
式中: a、b、c、d 分别为未知参数a、b、c、d的估计值。投影同步控制器为u=（u1，u2，u3）。

设投影同步误差为e1=y1-αx1、e2=y2-αx2、e3=y3-αx3，其中α为投影同步比例因子。未知参数估计误差设为：

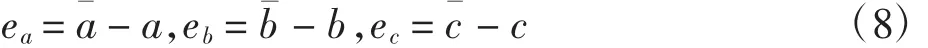
定理2当设计的投影同步控制器为：

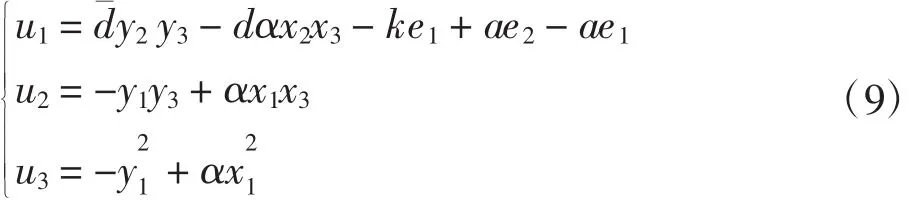
其中k≥0，未知参数辨识规则设计为：

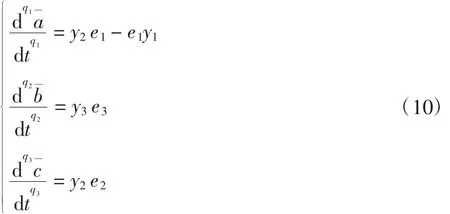
则驱动系统（6）和响应系统（7）达到投影同步，即：

证明根据系统方程（6）、（7）、（9），计算得到误差系统为：

针对该误差系统（11），设q1=q2=q3=q构造如下Lyapunov函数：

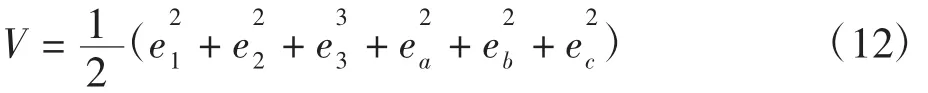
则V关于时间t的分数阶导数为：

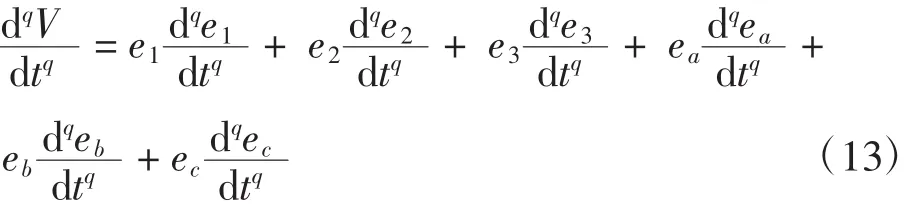
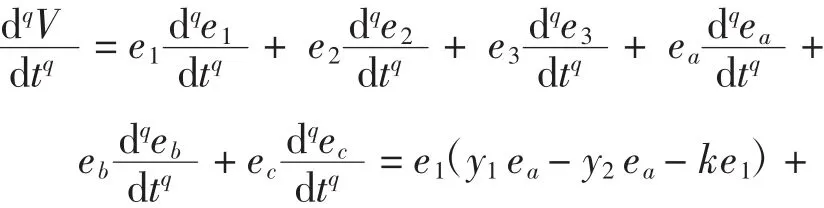
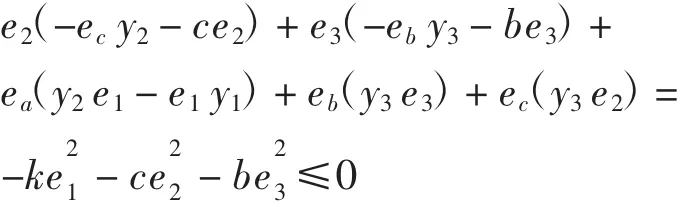
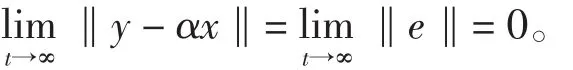
下面根据定理3，对误差系统（11）和参数辨识规则（10）进行证明。

证明构造如下形式的J函数：令q1=q2=q3=q

J=[e1，e2，e3，ea，eb，ec]·P6×·6

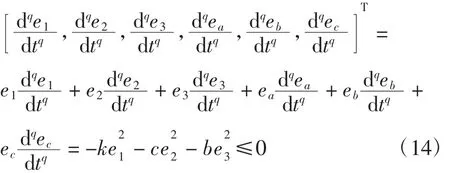
式中：k≥0；P6×6为6阶的单位矩阵。根据定理3，显然得出误差系统渐近稳定，同时不确定参数由估计值趋于真实值。

3　数值仿真

采用Matlab数值计算软件进行系统仿真。参数的真实值为（a，b，c）=（10，3，17），驱动系统（6）的初始值为（x（10），x（20），x（30））=（1，3，2），响应系统（7）的初始值为（y（10），y（20），y（30））=（-1，1，3），比例因子为α=0.3，同时k=10，参数估计值分别为（a，b，c）=（15，-1，1），得到投影同步误差图和参数辨识效果图。误差系统（11）的误差变化曲线如图2所示。由图2可以看到，误差函数e1和e3很快趋于0，同时e2随着时间t的增长最终也趋于0，也就是驱动系统和响应系统达到投影同步。未知参数辨识图如图3所示，由图3可以看出，a和b 很快由估计值趋近于真实值，c随着时间t的增长最终也趋于真实值，即所设计的辨识规则是正确的。

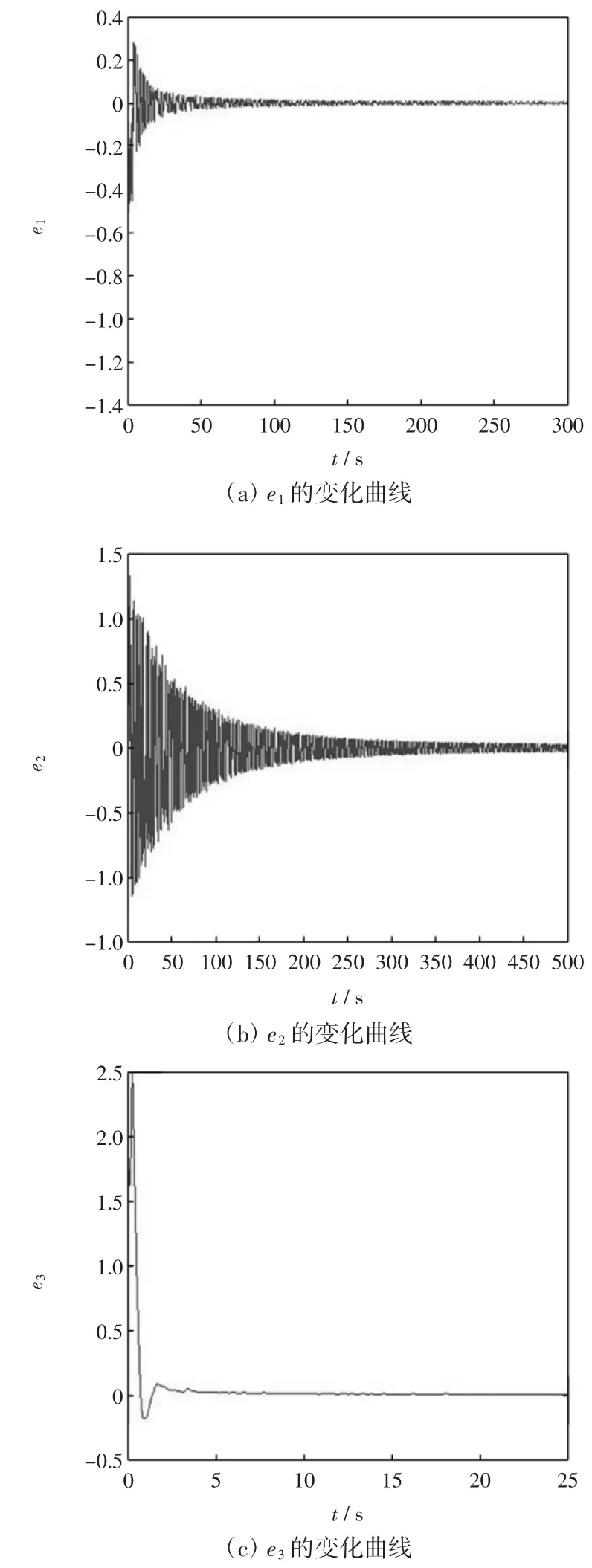
图2　误差系统（11）的误差变化曲线

4　结束语

基于分数阶稳定性理论，设计投影同步控制器与参数辨识规则，实现了驱动系统与响应系统的投影同步与参数辨识，利用Lyapunov稳定性理论和J函数法则给予证明，数值仿真验证了该方法的有效性和正确性。参考文献：

［1］PECORA L M，CARROLL T L. Synchronization in chaotic systems［J］. Physical Review Letters，1990，64（8）：821-827.

［2］李芳，胡爱花，徐振源.两个不相同系统的广义同步化［J］.物理学报，2006，55（2）：590-597.

［3］AGIZA H N，YASSEN M T. Synchronization of R觟ssler and Chen chaotic dynamical systems using active control［J］. Phys Lett A，2001，278（4）：191-197.

［4］MAINIERI R，REHACEK J. Projective synchronization in three-dimensional chaotic systems［J］. Phys Rev Lett，1999，82（15）：3042-3045.

［5］贾飞蕾，徐伟.一类参数不确定混沌系统的延迟同步［J］.物理学报，2007，56（6）：3101-3106.

［6］TAVAZOEI M S，HAERI M. Synchronization of chaotic fractional-order systems via active sliding mode controller［J］. Phys A Statistical Mechanics and Its Applications，2008，387 （1）：57-70.

［7］武相军，王兴元.基于非线性控制的超混沌Chen系统混沌同步［J］.物理学报，2006，55（12）：6261-6266.

［8］WANG Y，GUAN Z，WEN X. Adaptive synchronization for Chen chaotic system with fully unknown parameters［J］. Chaos，Solitons & Fractals，2004，19：899-903.

［9］张若洵，杨世平，刘永利.基于线性控制的分数阶统一混沌系统的同步［J］.物理学报，2010，59（3）：1549-1552.

［10］HAHN W. The Stability of Motion［M］. New York：Springer Press，1967.

［11］胡建兵，韩焱，赵灵冬.一种新的分数阶系统稳定理论及在back-stepping方法同步分数阶混沌系统中的应用［J］.物理学报，2009，58（04）：2235-2239.

［12］陈保颖，张家军，苑占江.分数阶Ruck lidge混沌系统的同步研究［J］.动力学与控制学报，2010，8（3）：234-238.

［13］杨叶红，肖剑，马珍珍.一个新分数阶混沌系统的同步和控制［J］.山东大学学报，2014，49（2）：76-84.

Two proofs for projective synchronization of one unknown parameter fractional-order chaotic system

KONG De-fu，ZHAO Xiao-shan
（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

Abstract：Based on the fractional-order stability theory，a universal projective synchronization controller and parameter identification rules are designed. The method is proved strictly by using Lyapunov stability theory and J function criterion. Numerical simulations are presented to verify the effectiveness and robustness of the control scheme.

Key words：fractional-order chaotic system；projective synchronization；parameter identification

作者简介：孔德富（1988—），男，硕士研究生；赵小山（1967—），男，副教授，博士，硕士生导师，研究方向为非线性动力系统分析.

基金项目：国家自然科学基金资助项目（11302158，11302148）；天津职业技术师范大学研究生创新基金资助项目（YC14-14）；天津市应用基础与前沿技术研究计划青年项目（15JCQNJC01600）.

收稿日期：2015-04-11

中图分类号：O415.5

文献标识码：A

文章编号：2095－0926（2015）03－0060－04