拉拉铜矿多岩层最终边坡稳定性数值模拟

吴淑冰，陈星明，2，张志贵，2，阿吉五作

（1.西南科技大学，四川绵阳621010；2.非煤矿山安全技术四川省高等学校重点实验室，四川绵阳621010；3.凉山矿业股份有限公司拉拉公司，四川凉山615000）

拉拉铜矿多岩层最终边坡稳定性数值模拟

吴淑冰1，陈星明1，2，张志贵1，2，阿吉五作3

（1.西南科技大学，四川绵阳621010；2.非煤矿山安全技术四川省高等学校重点实验室，四川绵阳621010；3.凉山矿业股份有限公司拉拉公司，四川凉山615000）

利用ANSYS有限元软件，基于强度折减原理，建立包含弹性及弹塑性两种本构的多岩层模型，对拉拉铜矿露天采场高边坡稳定性进行模拟分析，并给出边坡发生塑性破坏的过程。以塑性区从坡脚到坡顶贯通作为边坡破坏的标志，以《滑坡防治工程勘查规范》对边坡稳定安全系数划分的规定，判断在模拟得出的安全系数下边坡是否处于稳定状态。模拟分析表明，在不考虑节理裂隙和爆破振动等因素的影响下，拉拉铜矿原设计27°边坡角安全系数≥1.40，有足够的稳定性，当边坡角扩大到38°时，其安全系数仍可达到1.15，处于安全稳定状态。

多岩层边坡；ANSYS；强度折减法；Drucker-Prager准则

随着露天开采的延深，采场内所形成的高陡边坡规模是其他工程领域内所罕见的，边坡稳定性问题已成为主要的工程地质问题之一，因此有必要对边坡稳定性进行分析研究。边坡工程稳定性分析方法种类繁多，主要有极限平衡法、塑性极限分析法和有限元法［1-3］，各种分析方法都有各自的特点和适用范围［4-6］。近年来，计算机的飞速发展为利用数值模拟来研究边坡稳定性问题提供了便利，其中，有限元法是数值分析方法在边坡稳定评价中应用最早，也是最广泛的一种。

凉山矿业拉拉铜矿以铜矿为主要矿产资源，采用露天开采方式进行开采。矿山露天采场北部设计最低开采标高为＋1 890m，最高开采标高为＋2 224m，最终边坡高度334m，原始设计的最终边坡角约为27°。矿方计划扩大采矿权范围，开采低品位矿石，提出能否增加最终边坡角进行安全开采。

本文基于有限元强度折减法，根据矿山露天北部边坡赋存岩层的实际情况，不考虑边坡的节理裂隙及爆破振动等因素的影响，采用ANSYS有限元软件建立六个不同边坡角的多岩层边坡模型，对拉拉铜矿露天北部最终边坡角稳定性进行数值模拟研究，为矿山确定合理安全的最终边坡角提供依据。

1 有限元强度折减法理论及边坡失稳判据

1.1 强度折减法的基本原理

强度折减法是指将边坡体的抗剪强度指标黏聚力c和内摩擦角φ除以一个初始折减系数Fs进行折减，然后用折减后的cF和φF代替原来的c和φ作为新的强度参数参与下一轮的折减计算，并不断增大折减系数，如此不循环计算，直到边坡体发生剪切破坏，所对应的折减系数Fs为坡体的最小安全系数。强度折减法安全系数定义式为：

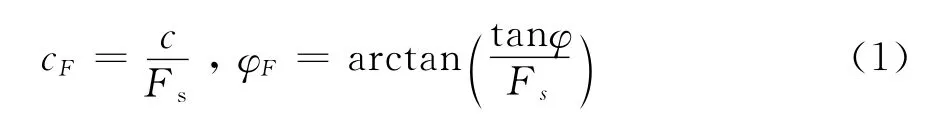
式中：cF—折减后的黏聚力；c—折减前的黏聚力；Fs—折减系数；φF—折减后的内摩擦角；φ—折减前的内摩擦角。

该式与经典极限平衡条分法所定义的强度储备系数（滑动面的抗剪强度与滑动面上实际剪力的比值）在本质上是一致的。

1.2 屈服准则

目前，许多流行的大型有限元软件如ANSYS以及MARC等均采用Drucker-Prager准则（以下简称D-P准则）：

式中：I1—张量第一不变量；J2—偏张量第二不变量；α、k—与黏聚力c和内摩擦角φ有关的常数。

在利用有限元进行数值模拟时，为与经典极限平衡条分法取得较一致的结果，通常通过变换公式（2）中的α和k，得到不同的D-P屈服准则［7］，如表1所示。

表1 各准则中参数α、k与c、φ的关系公式Table 1Relation formulas ofα、kandc、φin each criterion

1.3 边坡失稳破坏的判据

边坡失稳破坏判据目前还没有一个统一的标准，其中主要有两种观点最为常用：1）以有限元数值计算不收敛（发散）作为边坡失稳的标志；2）以塑性区从坡脚到坡顶贯通作为边坡破坏的标志。

郑颖人等人［8］认为上述两类判据所得到的安全系数相差不大，以计算收敛为判据求得的安全系数略大于以塑性区贯通求得的安全系数，两者相差1%左右，但以塑性区贯通判断边坡是否破坏失稳与极限状态假定一致且更客观一些，因此本文采用塑性区贯通原则来判断边坡是否失稳。

1.4 屈服准则及关联准则的选取

对于边坡问题，剪切因素造成了坡体的屈服，因而Mohr-Column准则是最适合用于边坡稳定性计算分析的准则，但该准则不利于实现数值计算，D-P准则更适合于数值计算［6，9］。而对D-P准则用于边坡稳定性分析不够精确的缺点，可通过修正得到适合不同条件下的D-P准则（如表1所示）。在利用ANSYS有限元软件进行边坡稳定性数值模拟计算时，其计算原理是通过弹性模型来计算滑体的位移和应力场，然后再通过定义单元表的形式将Mohr-Column准则引入，并对各个单元的屈服状态进行判断，从而得到满足Mohr-Column准则的边坡塑性区分布图，达到将M-C准则与D-P准则相结合、相互取长补短的目的。

郑颖人等［8-9］认为对于同一边坡，在使用同一屈服准则的情况下，不论采用非关联流动法则还是关联流动法则，所得的计算结果相差不大，但两者的相对误差随着内摩擦角的增大而增大，一般为3%～5%。张鲁渝等［10］认为采用关联流动法则所得到的破坏荷载比非关联流动法则的要大，当剪胀角为零时，边坡稳定系数更接近于极限平衡法，且与广义塑性力学理论相符，因此，本次模拟计算选择剪胀角为零即非关联流动法则所对应的DP5准则。

2 边坡数值模拟

2.1 模型建立

根据拉拉铜矿地质报告，矿山露天采场北部最终边坡所赋存的岩层从上往下分为四种岩组，依次为松散工程地质岩组、软质岩组、半坚硬岩组及坚硬岩组。各岩组的原始力学参数见表2，利用表1的转换公式，将表2的原始数据转换成DP5准则，所得的力学参数见表3。

将边坡模型设计为弹塑性层及弹性层两层，使模拟结果与设计概念相符［11］，构成最终边坡的四种岩组全部分布于弹塑性层上，弹性层的弹性模量与泊松比与坚硬岩组层相同。为了减小边界效应对计算结果的影响，取坡脚到左端边界的距离为坡高的1.5倍，即501m，坡顶到右端边界的距离为坡高的2倍，即668m，弹性层取300m，边坡模型及其网格划分如图1所示。本文建立27°、30°、33°、36°、38°、39°等六个边坡模型，初始折减系数都取值为1，此后每折减一次折减系数增加5%。通过模拟发现，边坡最顶层松散岩组层很不稳定，当设定边坡模型整体坡面角为27°时，刚进行初步计算该岩层就已经破坏（如图2所示），为了研究边坡整体的安全系数，将该岩层的坡度作减小处理，根据松散岩土的自然安息角及模拟结果，将此岩层的坡度设定为15°较为合适。

表2 各岩组的原始力学参数Table 2 Original mechanical parameters of all groups

表3 各岩组原始力学参数转换为DP5准则后的力学参数Table 3 Mechanical parameters of all groups after converting the original mechanical parameters to DP5criterion

图1 各岩组在边坡上的分布及网格划分示意图Fig.1 Distribution of all groups andmesh generation of the slope

2.2 计算与分析

模拟过程中采用平面应变问题，8节点单元类型，模型左右两侧水平约束，下部固定，上部为自由边界。计算考虑几何非线性（大变形）的影响，以塑性区从坡脚到坡顶贯通作为边坡破坏的标志。力和位移的收敛标准系数均取为0.000 01，一次性施加重力荷载，荷载子步设为1 000步。边坡模拟求解的内容为等效塑性应力。

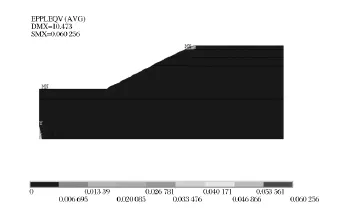
图2 松散岩层边坡角为27°、折减系数为1时塑性应变云图Fig.2 Plastic strain nephogram of loose rock formation at 27°when the reduction factor is 1

图3 Fs＝1时各边坡模型塑性应变云图Fig.3 Plastic strain nephogram of each slope model when the Fsis 1

图4 各边坡模型出现塑性贯通时塑性应变云图Fig.4 Plastic strain nephogram of each slope when the plastic transfixion occur

图3是初始状态即折减系数Fs为1时各边坡的塑性应变云图。

由图3的模拟结果可以看出，当折减系数（Fs）为1时，六个边坡模型都未发生塑性区贯通失稳，仍处于稳定状态。

图4是各边坡模型出现塑性贯通时塑性应变云图及所对应的折减系数。

由图4的模拟结果可以看出随着边坡角的增大，安全系数逐渐减小。当边坡角为27°、30°，折减系数达到1.40时，边坡只在坡脚出现破坏，整体未发生滑动，边坡处于稳定状态。当边坡角为33°、36°、38°、39°，折减系数分别达到1.35、1.25、1.15、1.10时，塑性区贯通，边坡发生剪切破坏，处于临界失稳状态，以此时的折减系数作为对应边坡的安全系数。根据表4可知，当折减系数Fs≥1.15，边坡是稳定的，所以在不考虑节理及爆破振动等影响因素的情况下，最终边坡角达到38°时边坡仍可保持稳定，从而说明拉拉铜矿露天北部原设计27°最终边坡角偏于保守，可扩大最终边坡角进行开采，但扩大之后的经济性还有待进一步研究。

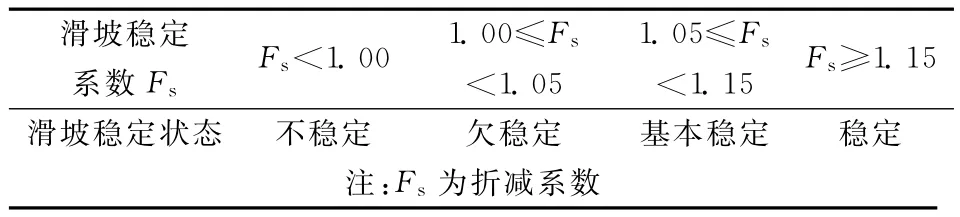
表4 《滑坡防治工程勘查规范》（DZ/T0218-2006）滑坡稳定状态划分Table 4 Classifications of landslide stable state in“specification of geological investigation for landslide stabilization”（DZ/T0218-2006）

3 结论

1）在合理地选用屈服准则并严格地控制有限元法的计算精度的情况下，将有限元强度折减法用于分析多岩层边坡的稳定性问题是可行的，该方法不仅能求出边坡稳定安全系数，并能直观的边坡失稳破坏的过程及滑动面的几何形状及位置。

2）拉拉铜矿北部最终边坡最上层的松散岩层的稳定性较差，在生产中为了保证安全，应先将该层先予以剥离或者采用削坡的方法，使其边坡角降低。

3）根据模拟结果及相关规范要求，在不考虑节理裂隙和爆破振动等因素影响的情况下，矿山原设计的27°最终边坡角的安全系数大于1.40，稳定性很好，当最终边坡角扩大到38°时安全系数为1.15，仍处于安全稳定状态，可见在保证安全的条件下可将最终边坡角扩大到38°。

［1］张鲁渝，时卫民，郑颖人.平面应变条件下土坡稳定有限元分析［J］.岩土工程学报，2002，24（4）：487-490.

［2］郑颖人，赵尚毅.有限元强度折减法在土坡与岩岩坡中的应用［J］.岩石力学与工程学报，2004，23（19）：3381-3388.

［3］刘正宇，李爱兵，邹平，等.丰山铜矿19线以西露天滑体边坡稳定性分析［J］.有色金属（矿山部分），2010，62（4）：43-46.

［4］宋登学，乔登攀.动静荷载作用下边坡的稳定性分析［J］.有色金属（矿山部分），2010，62（6）：46-48.

［5］郑 宏，李春光，李焯芬，等.求解安全系数的有限元法［J］.岩土工程学报，2002，24（5）：626-628.

［6］金文佳，杨 泽，侯克鹏，等.尖山边坡稳定性的三维动态数值模拟分析［J］.有色金属（矿山部分），2010，62（6）：42-45.

［7］赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24（3）：333-346.

［8］郑颖人.岩土材料屈服与破坏及边（滑）坡稳定分析方法研讨——"三峡库区地质灾害专题研讨会"交流讨论综述［J］.岩石力学与工程学报，2007，26（4）：649-661.

［9］赵尚毅，郑颖人，刘明维，等.基于Drucker-Prager准则的边坡安全系数定义及其转换［J］.岩石力学与工程学报，2006，25（增刊1）：2730-2734.

［10］张鲁渝，郑颖人，赵尚毅，等.有限元强度折减系数法计算土坡稳定安全系数的精度研究［J］.水利学报，2003（1）：21-27.

［11］王海斌，李永盛.边坡稳定性有限元分析的处理技巧［J］.岩石力学与工程学报，2005，24（13）：2386-2391.

Numerical simulation on multi-strata final slope stability of LaLa Copper Mine

WU Shubing1，CHEN Xingming1，2，ZHANG Zhigui1，2，AJI Wuzuo3
（1.Southwest University Science and Technology，Mianyang Sichuan 621010，China；2.Sichuan Province Higher Schools Key Laboratory of Non-Coal Mine Safety Technology，Mianyang Sichuan 621010，China；3.Lala Company，Liangshan Mining Co.，Ltd.，Liangshan Sichuan 615000，China）

Based on the strength reduction principle，the multi-strata slope model established by the finite element analysis software ANSYS contains two constitutive models which are elastic and elastic-plastic，to simulate and analyze the high slope stability of Lala open pit mine，and the plastic failure process is given.Using the plastic zone through from the toe to the top of slope as the sign of failure and estimating whether the slope still stabilization refer to the specification of geological investigation for landslide stabilization.The simulation analysis shows that：without considering the influence of blasting vibration and joint fissure factors，when the final slope angle is 27°，the safe coefficient is≥1.40，stability is sufficient.When the slope extended to 38°，the safety coefficient still can reach to 1.15，stability is sufficient too.

multi-strata slope；ANSYS；strength reduction method；Drucker-Prager

TD854＋.6

Α

1671-4172（2015）03-0098-05

吴淑冰（1989-），女，硕士，采矿工程专业，主要从事露天矿山境界及边坡稳定性方面的研究。

10.3969/j.issn.1671-4172.2015.03.022