三维有限元模拟伸直状态下不同软骨缺损面积对膝关节应力的影响

姬林松 李彦林 黄赞 贾笛 余洋 高寰宇 何川

昆明医科大学第一附属医院运动医学科（昆明650032）

软骨损伤在临床上常见， 未予治疗的损伤后期可能进展为骨关节炎，给患者带来极大痛苦[1]。 当前临床及动物模型研究均关注软骨损伤与骨关节炎之间的关系， 对于膝关节不同软骨缺损面积大小生物力学变化较少关注。 随着计算机虚拟技术的发展，建立膝关节三维数字模型模拟不同软骨缺损面积对膝关节接触应力影响成为可能[2，3]。 本研究利用正常人膝关节MRI二维图像，建立包含股骨、胫骨、内外侧半月板、内外侧副韧带、前后交叉韧带、髌骨及髌韧带的仿真膝关节数字化模型， 并分析位于股骨内侧髁不同软骨缺损面积对膝关节软骨及半月板接触应力的影响， 旨在明确软骨缺损与软骨退变的关系。

1 材料与方法

1.1 研究对象及主要仪器

随机选取1名健康成年男性为研究对象 （年龄27岁，身高160 cm，体重52 kg），无膝关节外伤史及风湿关节病史， 行X线及MRI检查排除膝关节骨折、 畸形、退变、半月板损伤、滑膜炎等病理变化。 GE1.5T超导型磁共振 （General Electric Company， 美国）。 戴尔工作站Precision T7500；CPU: Intel （至强）E5645 2.40 GHz 六核 （X2）； 内存：24 GB DDR3 1333 MHz； 硬盘：1 TB 7200转，SATA；显卡：NVIDIA Quadro4000 2 GB；操作系统：Windows7专业版（64 bit）。 交互式医学影像控制系统mimics 16.0软件 （Materialise's interactive medical image control system，Materialise公司，比利时，由西南交通大学计算机学院提供使用）。Geomagic Studio 12逆向工程软件（Geomagic公司，美国，由上海数造机电有限公司提供使用）。 Imgeware 13.0 逆向工程软件（EDS 公司， 美国， 由西南交通大学计算机学院提供使用）。Anasys 14.5有限元分析软件（ANSYS公司，美国，由西南交通大学计算机学院提供使用）。

1.2 研究方法

1.2.1 二维图像采集

采用GE 1.5 T 超导型磁共振机MRI 扫描， 获取二维图像，扫描体位：膝关节自然伸直并外旋10°～15°固定。 扫描参数设定为： 矢状位3D质子密度加权成像序列，TR 11000 ms，TE 25 ms； 层厚1.0 mm； 层间距0.2 mm；回波链14；激励2次；矩阵192/320；FOV 18。

1.2.2 建立三维模型

在计算机工作站上， 将膝关节MRI扫描图像以DICOM格式导入Mimics l6.0，定义上、下、左、右、前、后方向后，Mimics l6.0中显示出矢状位、冠状位、额状位的二维图像[4]。

在project Management>Contrast标签下调整窗宽窗位。 勾选“Fill holes”选项，单击Apply按钮,将分割结果保存为“蒙罩”。 使用区域增长功能将所要结构分离出来。 选择Segmentation> Region growing，将各个结构区域增长为不同颜色的蒙板， 将所需要的结构部分从二维图像中分离出。选择Segmentation> Calculate polylines命令计算膝关节内各种结构的轮廓线， 通过观察轮廓线判断膝关节内各种结构的蒙板边缘是否连续， 若发现不连续可以通过编辑蒙板工具进行编辑补充， 直到膝关节内各种结构的蒙板边缘连续完整， 然后重建出膝关节三维数字化模型。

1.2.3 建立三维数字化模型及定义弹性模量

将三维模型数据导入Geomagic Studio 12逆向工程软件，通过定位点配准、曲面优化等过程，运算出一个膝关节三维数字化模型。

在Hypermesh 11.0软件中对膝关节数字化模型进行网格划分，网格划分后最终构建成包含股骨、胫骨、腓骨、 内外侧副韧带等结构的完整膝关节三维有限元模型（见图1）。

图1 膝关节三维数字化模型及其部分相关结构

通过查阅文献，按表1定义弹性模量[5，6]。

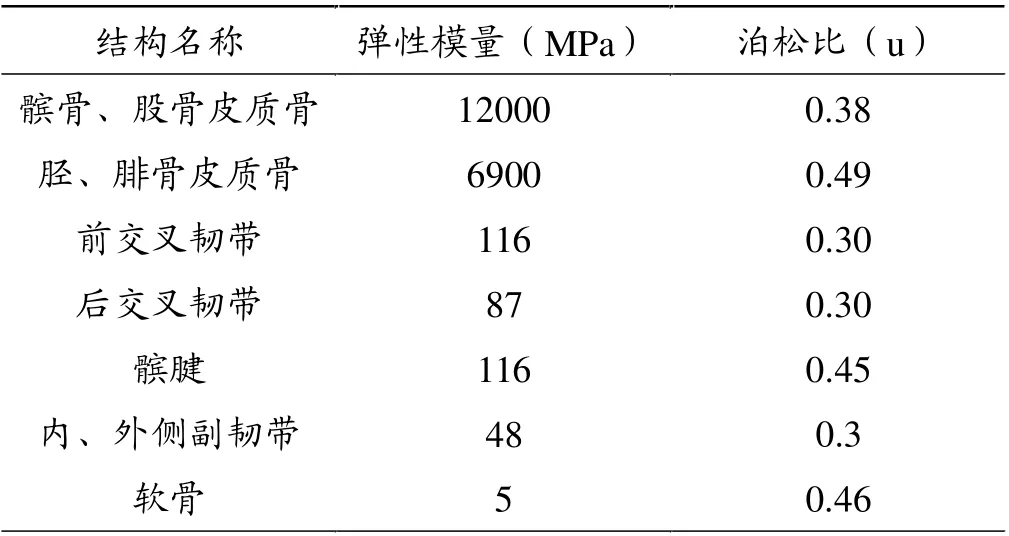
表1 膝关节三维数字化模型结构材料属性

1.2.4 软骨缺损模型建立

在膝关节数字化模型中于股骨内侧髁高负重区（内侧髁前部） 虚拟0.49 cm2, 0.80 cm2, 1.0 cm2, 1.70 cm2, 2.56 cm2, 3.24 cm2大小的缺损模型，深度足够达软骨下骨[2，7]。在股骨上施加1150 N垂直压应力，类似于步态周期中的伸直状态，以软骨缺损组为实验组、正常组为对照组分析膝关节软骨及半月板最大压应力与最大剪切应力。3名测试者分别对已建立的三维有限元模型进行分析， 分别得到关节软骨和半月板各部位应力分布图，经统计学计算得到3次分析结果的平均值及标准差。

1.2.5 统计学处理

2 结果

2.1 正常膝关节软骨有限元分析结果

由Von Mises应力分布图可见（图2）：对于正常膝关节，股骨内侧髁及外侧髁的前部软骨有较高的应力，最大压应力分别为2.9 ± 0.12 MPa和4.0 ± 0.17 MPa，双髁后部软骨最大压应力分别为0.9 ± 0.10 MPa 和0.7 ±0.09 MPa， 可见股骨内侧髁及外侧髁的前部为高负重区，而双髁后部为低负重区。 与股骨髁部类似，胫骨平台也存在高负重区与低负重区， 内侧胫骨平台及外侧平台软骨最大压应力分别为3.8 ± 0.11 MPa和1.9 ±0.25MPa。 而对于半月板，大部分应力集中于内侧半月板后角及外侧半月板前角， 最大压应力分别为3.1 ±0.12 MPa和5.1 ± 0.26 MPa。 故股骨髁及胫骨平台部软骨、半月板均存在低负重区及高负重区。

图2 正常膝关节软骨压应力分布情况

2.2 软骨缺损模型有限元分析结果

对正常膝关节软骨及半月板应力分析结果进行统计学分析，结果显示：软骨缺损组与正常组相比，股骨内侧髁及内侧胫骨平台关节软骨、 内侧半月板最大压应力及最大剪切应力均有统计学差异 （P＜0.05）（表2，表3）。 软骨缺损组与正常组相比，股骨外侧髁及外侧胫骨平台关节软骨、 外侧半月板最大压应力及最大剪切应力均无统计学差异（P＞0.05）。 由表2～4可见，软骨缺损组随着缺损面积增大， 软骨缺损边缘最大应力逐渐升高。 当缺损面积小于1.0 cm2时，缺损边缘最大剪切应力升高幅度较小，0.49 cm2与0.80 cm2缺损面积的剪切应力分别为2.5 ± 0.19 MPa和2.8 ± 0.16 MPa，相对于正常软骨（1.7 ± 0.22 MPa）分别增高了47% 和64%。 当缺损面积大于1.0 cm2时， 软骨缺损边缘应力集中非常明显。 1.0 cm2与1.70 cm2缺损面积的剪切应力分别为3.3± 0.10 MPa和3.4 ± 0.13 MPa， 相对于正常软骨 （1.7 ±0.22 MPa） 分别增高了94% 和100%。 2.56 cm2与3.24 cm2缺损面积的剪切应力分别为4.0 ± 0.15 MPa和4.5 ±0.08 MPa，相对于正常软骨（1.7 ± 0.22 MPa）分别增高了135% 和164%。

与剪切应力相似，由Von Mises应力分布图（图3）及表2可见缺损面积与软骨缺损边缘最大压应力之间的关系。 1.0 cm2与1.70 cm2缺损面积的压应力分别为5.5± 0.24 MPa和5.7 ± 0.19 MPa， 相对于正常软骨 （2.9 ±0.12 MPa）分别增高了89% 和97%。 2.56 cm2与3.24 cm2缺损面积的压应力分别为6.9 ± 0.20 MPa和8.1 ± 0.08 MPa， 相对于正常软骨 （2.9 ± 0.12 MPa） 分别增高了138% 和179%。 然而，缺损面积0.49 cm2与0.80 cm2的应力未见明显增高及重新分布， 压应力分别为4.5 ± 0.13 MPa和4.8 ± 0.15 MPa， 相对于正常软骨 （2.9 ± 0.12 MPa）分别增高了55% 和65.5%。

表2 软骨缺损组与正常组内侧间室最大压应力对比统计学分析（MPa ， ± s）

表2 软骨缺损组与正常组内侧间室最大压应力对比统计学分析（MPa ， ± s）

������� ��� �������� ��� ����� ��� 0.49 cm� 4.5���0.13� t=277.128�P=0.000� 4.4���0.23� t=8.660�P=0.�013� 6.3���0.22� t=55.426�P=0.000�0.80�cm�� 4.8���0.15� t=109.696�P=0.010� 6.8���0.23� t=58.260�P=0.000�1.0�cm�� 5.5���0.24� t=37.528�P=0.000� 4.6���0.25� t=9.897�P=0.001� 7.0���0.32� t=33.775�P=0.001�1.70�cm�� 5.7���0.19� t=69.282�P=0.001� 5.4���0.21� t=27.713��P=0.001� 7.8���0.26� t=58.147�P=0.000�2.56�cm�� 6.9���0.20� t=86.603�P=0.000� 6.6���0.22� t=44.089��P=0.000� 10.6���0.12� t=54.621�P=0.000�3.24�cm�� 8.1���0.08� t=225.167�P=0.000� 8.2���0.09� t=381.051�P=0.000� 11.8���0.33� t=71.756�P=0.000����� 2.9���0.12� � 3.8���0.11� � 3.1���0.12� �P=0.000� 8.5���0.05� t=135.677�

表3 软骨缺损组与正常组内侧间室最大剪切应力对比统计学分析（MPa ， ± s）

表3 软骨缺损组与正常组内侧间室最大剪切应力对比统计学分析（MPa ， ± s）

������� ��� �������� ��� ����� ��� 0.49 cm� 2.5���0.19� t=46.188��P=0.001� 3.5���0.18� t=190.53�P=0.003�0.80�cm�� 2.8���0.16� t=31.754��P=0.000� 2.4���0.05� t=25.981��P=0.002� 3.9���0.20� t=21.651�P=0.002�1.0�cm�� 3.3���0.10� t=23.094�P=0.001� 2.7���0.13� t=17.3216�P=0.006� 4.0���0.26� t=15.396�P=0.004�1.70�cm�� 3.4���0.13� t=32.717��P=0.002� 3.1���0.20� t=13.323��P=0.002� 4.5���0.32� t=15.155�P=0.004�2.56�cm�� 4.0���0.15� t=56.910��P=0.001� 3.9���0.22� t=20.785��P=0.001� 6.0���0.21� t=47.964�P=0.000�3.24�cm�� 4.5���0.08� t=34.641��P=0.000� 4.9���0.16� t=43.301�P=0.000� 6.8���0.09� t=762.102�P=0.000����� 1.7���0.22� � 2.1���0.07� � 2.4���0.08� �P=0.001� 5.1���0.19� t=225.167�

表4 缺损组股骨内侧髁软骨缺损边缘最大应力相对正常组升高百分比（%）

最大压应力及最大剪切应力升高幅度最大处均位于0.8 cm2和1.0 cm2之间，考虑0.8 cm2可能为分界线。 随着缺损面积增大，股骨内侧髁缺损边缘软骨、内侧半月板及内侧胫骨平台软骨无论是最大压应力及最大剪切应力，均明显升高。故股骨内侧髁软骨缺损对膝关节内侧间室应力影响较大， 尤其缺损面积较大者（>0.8 cm2），缺损边缘应力集中更为明显。 而且内侧半月板的最大压应力及最大剪切应力数值均较膝关节其他部位大。

图3 股骨内侧髁软骨缺损边缘最大压应力分布情况

3 讨论

本研究利用MRI二维图像重建的数字化模型包括股骨、胫骨、内外侧半月板、内外侧副韧带、前后交叉韧带、髌骨及髌韧带等膝关节主要结构，建立了高保真度的膝关节数字化模型， 从而确保获得的接触应力更接近实际情况。Pena等[2]报道的模型并未包括内外侧半月板、内外侧副韧带、前后交叉韧带、髌骨及髌韧带等主要结构，应用垂直应力时，由于没有韧带限制，股骨可能相对胫骨发生前移，模型过于简单。实验主要目的是研究膝关节处于伸直状态下股骨软骨、 胫骨软骨及半月板的应力变化，因伸直时髌骨受力非常小[5]，故未考虑髌骨软骨的应力变化。

对于正常膝关节，我们发现内侧半月板后角、外侧半月板的前角、 股骨内侧髁及内侧胫骨平台软骨均有较高的应力，说明上述部位为高负重区，与Bendjaballah等[8]的研究相符。

既往研究仅分析股骨内侧髁软骨缺损边缘应力变化[2]，而本实验对软骨缺损组与正常组股骨内外侧髁及内外侧胫骨平台关节软骨、 内外侧半月板最大压应力及最大剪切应力均进行了统计学分析。 结果发现无论是最大压应力峰值还是最大剪切应力峰值， 软骨缺损组与正常组相比， 股骨内侧髁及内侧胫骨平台关节软骨、内侧半月板均有统计学差异（P＜0.05），而股骨外侧髁及外侧胫骨平台的关节软骨、 外侧半月板均无统计学差异（P＞0.05）。 说明股骨内侧髁软骨缺损对膝关节内侧间室应力影响较大。Bingham等利用有限元方法分析，也发现内侧间室软骨接触变形要大于外侧间室，因为内外侧胫骨平台的解剖学差异， 内侧间室接触面积相对也要大些， 所以内侧间室软骨的接触应力大于外侧间室[9]。

由实验数据可知软骨缺损组股骨内侧髁的最大剪切及压应力均高于股骨外侧髁，而Papaioannou等在内外侧髁虚拟同样大小的缺损仍发现股骨内侧髁的应力高于股骨外侧髁[10]，Widuchowski等经过长期临床随访发现Outerbridge 1～4级股骨内侧髁软骨损伤例数均明显高于股骨外侧髁， 说明股骨内侧髁相对于股骨外侧髁更容易损伤[1]。所以我们建立的模型软骨缺损处位于内侧髁[11]。 而内侧半月板的最大压应力及最大剪切应力数值均较膝关节其他部位大， 说明内侧半月板在传递负荷、缓冲震荡、增加关节接触面等方面起着非常重要的作用[12]。

临床上选用骨膜、 自体软骨细胞移植等方法治疗软骨缺损的临界点有很多：0.75 cm2，1 cm2和1.2～1.6 cm2等[10]。 Pena等[2]发现面积较大的缺损（>1 cm2）边缘应力增加明显，所以他们认为>1 cm2是分界线。 而本实验结果显示剪切及压应力升高幅度最大位置均位于0.8 cm2和1.0 cm2之间， 但是缺损面积1.0 cm2和1.70 cm2之间应力升高并不是非常明显， 这提示分界线效应确实存在。0.8 cm2可能是重要的分界点，而Papaioannou等同样认为0.8 cm2是软骨缺损的分界线[10]。 既往研究表明，较大面积的软骨缺损相对小的软骨缺损常常有较差的临床结果， 可能预示着软骨的退变与软骨缺损面积有较大的关系[2]。 因为对于较大的软骨缺损，负重区域应力再分布导致缺损边缘软骨因负重增加而出现关节内流体压降低， 继而出现软骨营养不良及关节摩擦力增加，从而出现正常软骨退变[13]。

本实验仍存在一些局限性。 首先，实验分析膝关节伸直位时膝关节各部位的应力变化， 而没有进行动态模拟分析；其次，软骨缺损模型为不同面积的四方形，可能与临床的实际情况有一定差别。 尽管存在以上局限性， 本实验仍有助于了解不同缺损面积对膝关节应力变化的影响，为临床工作提供理论依据。

[1] Widuchowski W, Widuchowski J, Trzaska T. Articular cartilage defects: study of 25,124 knee arthroscopies.Knee,2007, 14(3): 177-182.

[2] Pena E, Calvo B, Martínez MA, et al. Effect of the size and location of osteochondral defects in degenerative arthritis. A finite element simulation. Comput Biol Med, 2007, 37(3):376-387.

[3] Dong YF, Hu GH, Zhang LL, et al. Accurate 3D reconstruction of subject-specific knee finite element model to simulate the articular cartilage defects. Journal of Shanghai Jiaotong University (Science), 2011, 16: 620-627.

[4] 黄赞, 李彦林, 胡猛, 等. 基于MRI 和CT 二维图像重建膝关节三维数字化模型的股骨髁扭转角差异性研究. 中国修复重建外科杂志, 2015, 2(29): 167-170.

[5] Pena E, Calvo B, Martinez MA, et al. Finite element analysis of the effect of meniscal tears and meniscectomies on human knee biomechanics. Clin Biomech (Bristol, Avon), 2005, 20(5): 498-507.

[6] Innocenti B, Truyens E, Labey L, et al. Can medio-lateral baseplate position and load sharing induce asymptomatic local bone resorption of the proximal tibia? A finite element study.J Orthop Surg Res, 2009, 4: 26.

[7] Saarakkala S, Julkunen P, Kiviranta P, et al. Depth-wise progression of osteoarthritis in human articular cartilage:investigation of composition, structure and biomechanics.Osteoarthritis Cartilage, 2010, 18(1): 73-81.

[8] Bendjaballah MZ, Shirazi-Adl A, Zukor D. Biomechanics of the human knee joint in compression: reconstruction, mesh generation and finite element analysis. Knee, 1995, 2(2): 69-79.

[9] Bingham J, Papannagari R, Van de Velde S, et al. In vivo cartilage contact deformation in the healthy human tibiofemoral joint. Rheumatology, 2008, 47(11): 1622-1627.

[10] Papaioannou G, Demetropoulos CK, King YH. Predicting the effects of knee focal articular surface injury with a patientspecific finite element model. Knee, 2010, 17(1): 61-68.

[11] Carter DR, Beaupre GS, Wong M, et al. The mechanobiology of articular cartilage development and degeneration. Clin Orthop Relat Res, 2004, 427(427 Suppl): S69-77.

[12] Scheller G, Sobau C, Bülow JU. Arthroscopic partial lateral meniscectomy in an otherwise normal knee: clinical,functional, and radiographic results of a long-term follow-up study. Arthroscopy, 2001, 17(9): 946-952.

[13] Dabiri Y, Li LP. Altered knee joint mechanics in simple compression associated with early cartilage degeneration.Comput Math Methods Med, 2013, 2013: 862903.