基于主从加权灰色关联的模型综合一致性检验*
2015-04-15宁小磊吴颖霞
宁小磊,吴颖霞,赵 娜
(1 中国华阴兵器试验中心制导武器试验鉴定仿真技术重点实验室,陕西华阴 714200;2 中国白城兵器试验中心,吉林白城 137000)
基于主从加权灰色关联的模型综合一致性检验*
宁小磊1,吴颖霞1,赵 娜2
(1 中国华阴兵器试验中心制导武器试验鉴定仿真技术重点实验室,陕西华阴 714200;2 中国白城兵器试验中心,吉林白城 137000)
为了全面检验仿真模型的一致性,提出了一种基于主从加权灰色关联的模型综合一致性检验方法。主加权过程依据各阶段的相对重要性对各个阶段赋权,分别计算各阶段的灰色关联度。从加权过程根据参考数据与行为序列数据之间的误差进行灰色关联系数的权值确定,最后进行综合一致性检验。同时,考虑了曲线之间的距离,减小了灰色关联模型验证的风险。最后,通过实例分析与比较验证了改进灰色关联度模型验证方法的有效性和实用性。
模型验证;一致性检验;灰色关联分析;主从加权;仿真
0 引言
系统建模与仿真技术已成为靶场工程师进行定型与鉴定工作最重要的手段之一,然而在实际应用时存在的最大难度是评估靶场所建立的系统模型的可信性,因为没有经过验证的模型根本无法获得各方的认可,仿真模型的有效性将直接影响系统建模与仿真技术在靶场的应用程度。目前,仿真模型有效性检验最基本、最直接的方法就是考察相同初始条件下仿真模型输出与实际系统输出是否一致[1]。灰色关联在序列一致性分析方面具有明显的优势[1-8],该方法对检验样本量的多少和分布规律没有严格要求,也不需要对数据进行预先处理,避免了人为因素影响检验结果。灰色关联分析有诸多优点,然而将其应用于模型验证时仍存在以下风险:1)灰色关联度是一个整体平均的概念,对系统工作各阶段“一视同仁”,实际上多个阶段对系统整体性能影响并不同。比如对具有主动段、中制导段和末制导段的弹道,使用者更关注主动段和末制导段性能,因此模型综合性检验中权重应该较大。2)在灰色关联度的计算过程中,对每个灰色关联系数“一视同仁”平均加权,实际上为了更精细的进行模型检验,仿真误差大的时序点对灰色关联结果贡献应更小。3)灰色关联度关注曲线形状而忽略曲线间的距离。文中根据靶场仿真模型综合检验的需求,同时为了减小模型验证的费用和风险,提出了一种基于主从加权灰色关联的仿真模型综合性一致性检验方法。主加权根据系统工作各阶段对整体性能的影响程度进行确定;从加权根据仿真数据与实际数据的误差进行确定,从加权的这一思想同时将距离接近性引入灰色关联度计算中,避免了灰色关联分析主要依据序列曲线几何形态的相似程度进行关联判断,并没有考虑曲线之间的接近程度,从而引起的决策风险。最后进行了仿真分析与算法验证。
1 基于主从加权灰色关联的模型综合一致性检验
1.1 主从灰色关联度模型构建
系统的工作过程通常包括多个阶段,人们对各个阶段的工作过程关注度并不同,且各个阶段对系统整体性能的影响程度也不同,因此各个阶段的仿真结果对系统整体仿真结果的一致性影响应该也不同。根据这一分析思路,在模型一致性检验时,应根据系统对象的实际特点,将其划分为各个阶段,根据各个阶段的相对重要性程度,采用层次分析等赋权方法确定各阶段的权重,最后进行综合一致性计算。称此过程为主加权。
同时,灰色关联度更关注曲线的形状,并不过多关注曲线间的相对距离,但在仿真领域曲线间的相对距离才是最重要的仿真误差。为了减小这一缺陷引起的决策风险,文中通过负指数形式将距离概念引入对各个灰色关联系数进行赋权,最终的结果是仿真误差大的时序点对灰色关联度贡献小。称这一过程为从加权。根据以上两过程进行灰色关联分析称为主从加权灰色关联分析。
具体模型构建如下:
设系统参考序列为:
系统行为序列为:
定义灰色关联系数为
γ(x0,xi)=(exp(-|x0(k)-x1(k)|)/ξ)α×
(1)
式中,α,β∈(0,1)且满足α+β=1,为调节系数,它们反映了系数对灰色关联系数的影响程度,实际上也是平衡曲线形状与曲线距离的参数。ξ为比例系数,根据实际经验获取。
假设根据系统工作特性将其划分为m个阶段,则主从加权灰色关联度为:
(2)
主从加权灰色关联度计算过程如图1所示。

图1 主从加权灰色关联度计算流程
1.2 基于主从加权灰色关联的模型综合一致性检验
基于主从加权灰色关联的模型综合一致性检验的步骤如图2所示。

图2 改进的灰色关联模型验证
2 实例应用与分析
2.1 算例1——改进模型的优势分析
本算例说明主从加权灰色关联较常规灰色关联的优势:
算例具体描述如下:
参考序列:x0=[44 65 64 43 40]
行为序列:xi= [44 65 64 43 40]+
η×[10 10 10 10 10]
式中:η为系数,取不同值便得到与参考序列不同的行为序列。如图3给出了η=0.1∶0.1∶1时的参考序列和行为序列。

图3 参考序列和行为序列曲线图
为了便于分析,使用常规灰色关联度模型(GR)、主从加权灰色关联度模型(WGR)和TIC分别进行计算,计算结果如表1所示。由表1可以看出,GR对此算例不敏感,其关联度均为0.333 3,这说明GR忽略了曲线距离;WGR和TIC计算结果均表明随着行为序列距离参考序列越来越远,其关联度越小,这与实际情况相符合,也说明该方法的有效性。同时,取了3组α、β值进行了计算,α值较大时,说明在关联分析中更关注曲线距离,α值较小时,说明在关联分析中更关注曲线形状。

表1 各关联度模型的计算结果
2.2 算例2——改进模型的应用
以某型导弹飞行速度为研究对象,对其综合一致性进行检验。该型号导弹发射后,发动机点火进行加速,加速结束后,导弹自由飞行。根据导弹的实际飞行过程,可将其分为2个阶段,加速段和自由飞行段。图4给出了一次飞行试验数据和两次仿真试验数据曲线。
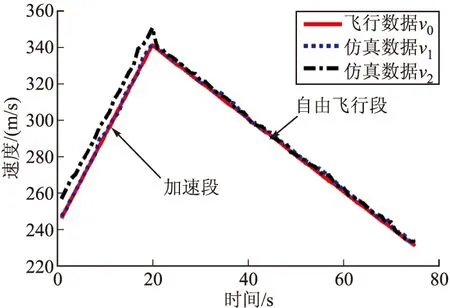
图4 飞行试验和仿真试验数据曲线图
使用GR、WGR和TIC分别求取加速段和自由飞行段的灰色关联度,如表2所示。从图4可以看出,在加速段,模型1的精度好于模型2,GR、WGR和TIC三种方法均给出了正确的关联结果;自由飞行段GR、WGR和TIC三种方法也给出了一致的关联结果,说明该方法的有效性。
最后可以对飞行试验数据与仿真试验数据的一致性进行综合性检验。假设通过层次分析法得到加速段和自由飞行段的权重为w=[0.6 0.4],则加权综合结果为:γ1=0.853 1,γ2=0.600 6。若直接使用灰色关联方法,则其关联结果分别为γ1=0.842 4,γ2=0.699 0。两种方法都说明模型1与实际飞行结果一致性更好,选择模型1模拟实际飞行过程。
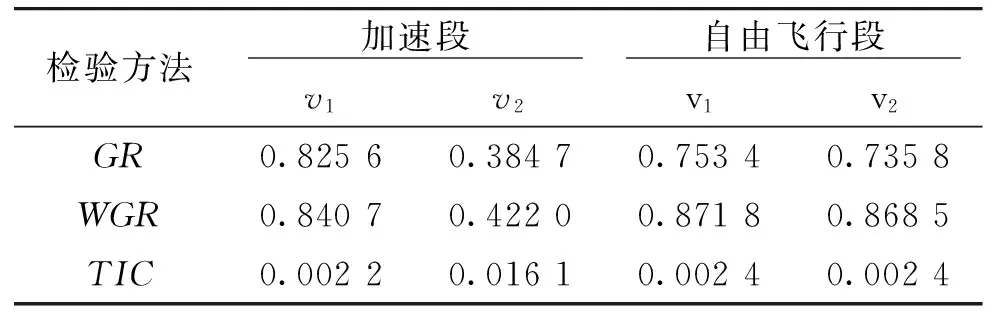
表2 各关联度模型的计算结果
3 结束语
仿真模型一致性检验是靶场进行仿真试验最重要的内容之一,文中针对靶场仿真模型验证的特殊需求,以及将常规灰色关联分析应用于模型验证时存在的风险,提出了一种基于主从加权灰色关联的模型综合一致性检验方法。该方法根据系统工作特点以及系统各阶段对系统整体性能的影响程度,使用层次分析等赋权方法对数据进行了综合一致性检验。同时通过负指数形式将曲线距离以从加权的形式引入灰色关联系数计算中,减小了灰色关联分析的风险。最后,通过算例检验了主从加权灰色关联的有效性和可行性。
[1] 魏华梁, 李钟武. 灰色关联分析及其在导弹系统仿真模型验证中的应用 [J]. 系统工程与电子技术, 1997, 19(2): 55-61.
[2] 胡玉伟, 马萍, 杨明, 等. 基于改进灰色关联分析的仿真数据综合一致性检验方法 [J]. 北京理工大学学报, 2013, 33(7): 711-715.
[3] 孙勇成, 周献中, 李桂芳, 等. 基于灰色关联分析的仿真模型验证及其改进 [J]. 系统仿真学报, 2005, 17(3): 522-525.
[4] 刘思峰. 灰色系统理论及其应用 [M]. 北京: 科学出版社, 1999.
[5] 胡方, 黄建国, 张群飞. 基于灰色系统理论的水下航行器效能评估方法研究 [J]. 西北工业大学学报, 2007, 25(3): 411-415.
[6] 宁小磊, 赵娜, 吕永佳, 等. 基于阵灰色关联分析的仿真模型验证方法研究 [J]. 弹箭与制导学报, 2014, 34(3): 203-205.
[7] 李群, 吴勇, 张建东. 基于相似理论的综合航电系统仿真可信度研究 [J]. 弹箭与制导学报, 2006, 26(2): 804-807.
[8] 郑昕, 吴勇, 孙琦. 基于广义相似论的航空电子综合系统仿真可信度研究 [J]. 弹箭与制导学报, 2009, 29(4): 255-258.
Study on Comprehensive Consistency Test of Models Based on Double Weighted Gray Relational
NING Xiaolei1,WU Yingxia1,ZHAO Na2
(1 Key Laboratory of Guided Weapons Test and Evaluation Simulation Technology, Huayin Ordnance Test Center of China,Shaanxi Huayin 714200, China; 2 Baicheng Ordnance Test Center of China, Jilin Baicheng 137000, China)
In order to improve quality of consistency test, a new relational model named double weighted gray relational was proposed. The first structure was main frame of the new model, in which the process of system was divided into many phases by its practical characteristics in work, and then different phases were weighted by its contribution to the whole system. The second weight was to improve the accuracy of model. Its weight was fixed by the distance of reference data and test data. By doing this, the new model was in view of the similarity by subtraction and the nearness by division between the simulation and flight-test time series, so it had higher accuracy and reliability. Finally, two case studies were given to show reasonability and validity of the improved model.
validation of simulation models; consistency test; gray relational analysis; double weighted; simulation
2014-07-29
宁小磊(1985-),男,陕西华阴人,工程师,硕士研究生,研究方向:兵器试验鉴定技术。
TJ761.12
A
