潜射远程弹道导弹弹道折合方法研究*

佟力永,王浩宇,肖 凡

(1 海军装备部,北京 100800;2海军潜艇学院,山东青岛 266042)

潜射远程弹道导弹弹道折合方法研究*

佟力永1,王浩宇1,肖 凡2

(1 海军装备部,北京 100800;2海军潜艇学院,山东青岛 266042)

针对潜射远程弹道导弹弹道折合,用数理统计分析方法建立了初始误差折合模型,用平台漂移原理建立了工具误差折合模型,用线性假设的方法建立了其它误差折合模型。提出了基于试验数据、误差折合模型和弹道仿真的弹道折合方法,详细阐述了该方法的实施步骤。验证及计算表明,弹道复现结果与试验数据吻合度好,折合结果与理论分析一致。

潜射远程弹道导弹;弹道折合;初始误差;误差模型;弹道仿真

0 引言

远程弹道导弹的飞行试验受国土面积、国际环境、外交政治等诸多因素的影响,难以进行全射程试验。因此,由小射程试验数据,精确预示大射程或者全射程下的落点对于射程、精度等战术技术指标的考核具有重要意义,采用的方法一般是弹道折合。弹道折合涉及误差分离、折合,弹道建模及仿真等技术。潜射方式相对静基座发射方式,误差源增多,诸元计算更加复杂,尤其是潜射远程弹道导弹,误差影响更为明显,其弹道折合也最为困难。文献[1-2]利用改进的主成分方法,并采用遗传算法选择最佳主成分子集,有效提高了工具误差折合精度;文献[3]对远程反舰导弹试验弹道折合进行了分析,重点研究了自控终点散布的折合,文献[4-5]研究了海态环境下的初始误差和工具误差的分离方法。上述成果对研究潜射远程弹道导弹弹道折合在某些方面具有借鉴作用,但均未对该问题进行全面分析。文中就潜射方式下,远程弹道导弹的弹道折合问题进行系统研究。

1 弹道折合的基本思路

潜射远程导弹弹道折合应该尽可能的考虑各种干扰因素,尽量准确的建立各种误差模型,根据试验弹的运动轨迹建立精确的控制和弹道仿真模型。弹道折合的关键是由试验数据建立折合状态下相关参数合理的预测模型,这其中的关键就是各种误差的折合。潜射方式下,导弹发射时的定位、定向、初速误差对导弹飞行轨迹及落点影响较大,弹道折合时应该重点研究。本方法弹道折合采取如下三大步:根据试验数据进行误差分离→结合误差分离结果建立折合状态下的误差模型→折合状态下弹道仿真,得出折合结果。具体过程如图1所示。其中,虚线“初始误差分离[4]”表示这一部分工作可能不进行(试验弹道为静基座状态);虚线“初始误差”表示这部分数据可能不存在(试验弹道为静基座状态)。

图1 潜射方式弹道折合基本思路

2 误差建模

弹道折合是建立在试验数据误差分离的基础之上,关键是折合状态下各项误差模型的确定。下面就误差建模的相关问题进行研究。

2.1 初始误差

所谓初始误差是指由潜射方式引起的误差,包括定位、定向误差[4]及初速误差[4]。根据小射程试验发射方式的不同,初始误差的折合方法也不同。如果小射程试验的发射基座与大射程为同一潜艇或者同型号的潜艇,这种情况下初始误差无需折合,直接采用小射程试验数据的初始误差分离结果;如果不是上述情况,则需要生成初始误差,以供潜射方式大射程使用,不论小射程试验是静基座还是其它型号的潜艇,初始误差的生成文中采取相同的方法:统计生成法,具体做法如下。

首先,对大射程状态下的发射潜艇相关试验数据进行统计分析[6],建立定位、定向以及速度误差的统计模型[6],然后依据统计模型产生随机数据,作为初始误差数据。

定位、定向及速度误差分解成标量为9个元素,设Xi为测量均值,Si为样本方差,由概率统计知识,Si为标准差δi的一致估计量,因此,可设初始误差Yi的统计模型为:

(1)

通过式(1)采取随机抽样的方法对每发的初始误差进行赋值。

2.2 工具误差

剔除初始误差影响后,不同发射方式及不同射程情况下,假定工具误差系数与环境函数无关,则工具误差具有相同的规律,因此,搞清楚小射程试验状态下的工具误差模型,潜射大射程下工具误差模型也就确定了。惯性平台是工具误差产生的主要部件,其漂移角由陀螺仪漂移、平台回路静态及动态误差组成,设αip表示i方向上平台的漂移角,则T时刻的误差如下[7]:

(2)

其中,漂移误差模型[7]为:

静态误差模型[7]为:

动态误差模型[7]为:

各项系数具体含义见文献[7],限于篇幅这里不再赘述。

通过小射程试验数据,分离出式(2)中各项误差系数,潜射大射程弹道折合时即可运用式(2)进行工具误差的实时修正。

2.3 其它误差

其它误差是指除初始误差和工具误差后影响弹道折合精度的其它各项误差,主要包括方法误差、中段误差和再入误差。制导方法误差、中段误差和再入误差对弹道折合精度的影响相对较小,利用遥外测数据信息,采用适当的误差分析方法[8],可求解出制导方法误差、中段误差及再入误差。随着制导方案的完善,方法误差的影响已经非常小,远程导弹弹道折合时可以不予考虑。

(3)

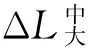
3 折合流程

弹道折合建立在误差分离基础之上,误差分离这里不进行研究,具体方法可以参见文献[1,4-5,9]等相关资料。小射程试验数据误差分离完毕后,弹道折合的流程如图2所示。

图2 弹道折合流程图

大射程标准弹道仿真:初始误差置零,同时将大射程飞行程序、平台误差系数地面测定值、发射点信息代入弹道仿真软件进行仿真,获取全弹道数据。

初始误差生成:小射程试验的发射基座与大射程发射为同一潜艇或者同型号的潜艇时,采用小射程试验数据的初始误差分离结果作为初始误差;若不是上述情况,则根据需要生成数据的数量视情况采用式(1)生成初始误差数据。

工具误差生成:采用试验数据误差分离结果标定式(2)中各误差系数,作为工具误差的计算公式。

大射程干扰弹道仿真:将生成的初始误差、工具误差和其它误差,大射程飞行程序和发射点信息代入弹道仿真软件进行仿真,获取干扰弹道全弹道数据。

折合结果分析:通过“大射程干扰弹道仿真”结果可得折合弹道数据;对比“大射程干扰弹道仿真”和“大射程标准弹道仿真”结果可得各项误差数据。

4 验证及算例

依据第3节中所述折合步骤,对某型号的两次潜射1 500 km试验数据进行6 000 km的大射程折合,为了便于说明,两次试验分别命名为S1和S2,S1采用潜艇A发射,S2以及待折合大射程均采用潜艇B发射,A与B为不同型号潜艇。表1为试验数据误差分离结果,作为弹道折合输入数据的一部分,由于工具误差系数项目较多,限于篇幅表中没有列举。

表1 试验数据误差分离结果

将S1和S2的相关数据代入,按照第3节中“大射程标准弹道仿真”的方法,即可得到大射程下S1和S2对应的理论速度;按照第3节中“大射程干扰弹道仿真”的方法,即可得到大射程下S1和S2对应的折合速度。图3为大射程下标准弹道的速度与干扰弹道速度差,折合后的落点误差与试验落点误差关系如表2所示。由表2有,随着射程的增大,干扰对纵向偏差的影响呈减弱的趋势,对横向偏差的影响明显加强,这与理论定性分析的结果[7]一致。

图3 大射程下标准弹道与干扰弹道速度差

落点偏差/m 试验S1 试验 大射程折合 试验S2 试验 大射程折合纵向偏差ΔL L10.563L1 L20.313L2横向偏差ΔH H11.685H1 H22.143H2

5 结论

文中建立了潜射远程导弹弹道折合时初始误差、工具误差及其它误差的生成模型,提出了基于试验数据、误差折合模型和弹道仿真的弹道折合方法,以及实施步骤。弹道复现和算例表明,文中所提出的方法易于实施,折合结果可信度高,能够有效解决潜射远程导弹弹道折合的难题。

[1] 夏青, 杨华波, 张士峰, 等. 基于遗传算法的工具误差分离与弹道折合 [J]. 系统仿真学报, 2007, 19(18): 4130-4133.

[2] 杨华波, 张士峰, 夏青. 弹道折合的遗传主成方法 [J]. 飞行器测控学报, 2007, 26(6): 54-58.

[3] 李鹏波, 蔡洪, 张湘平. 远程反舰导弹试验弹道折合方法研究 [J]. 战术导弹技术, 1998(3): 11-15.

[4] 胡正东, 杨华波, 张士峰. 潜射导弹初始误差与制导工具误差分离研究 [J]. 弹箭与制导学报, 2006, 26(3): 46-52.

[5] 姚静, 段小君, 周海银. 海态制导工具系统误差建模与参数估计 [J]. 弹道学报, 2005, 17(1): 33-39.

[6] 张金槐, 蔡洪. 飞行器试验统计学 [M]. 长沙: 国防科技大学出版社, 2004.

[7] 陈世年. 控制系统设计 [M]. 北京: 宇航出版社, 1996.

[8] 张金槐, 贾沛然, 唐雪梅. 远程火箭精度分析与评估 [M]. 长沙: 国防科技大学出版社, 1995.

[9] 蒋小勇. 潜射弹道导弹弹艇误差分离技术研究 [D]. 长沙: 国防科技大学, 2008.

Research on Trajectory Conversion Method for Submarine-launched Long Range Ballistic Missiles

TONG Liyong1,WANG Haoyu1,XIAO Fan2

(1 Navy Armament Division, Beijing 100800, China; 2 Navy Submarine Academy, Shandong Qingdao 266042, China)

An initial error conversion model of submarine-launched long range ballistic missiles was established by mathematical statistical analysis method. A platform tool error conversion model was established by platform drift principles, and other error conversion models were established by linear hypothesis method. A trajectory conversion method was proposed based on test data, error conversion models and trajectory simulation. The implementation steps of the method were elaborated. Validation and calculations show that ballistic reproduction corresponds with the experimental data, and the conversion results are consistent with the theoretical analysis.

submarine-launched long range ballistic missile; trajectory conversion; initial eror; error model; trajectory simulation

2014-07-26

佟力永(1978-),男,辽宁凌海人,工程师,硕士,研究方向:导弹性能分析与设计。

V417.7

A