一种基于Pareto排序的混合多目标进化算法

吴坤安，严宣辉，陈振兴

福建师范大学 数学与计算机科学学院，福州 350007

1 引言

最优化问题是工业设计、城市规划和管理科学领域广泛研究和探讨的问题，其中仅有一个目标函数的最优化问题称为单目标优化问题，目标函数超过一个并且需要同时处理的最优化问题称为多目标优化问题（Multi-objective Optimization Problems，MOPs）。对于多目标优化问题，一个解对于某个目标来说可能是较好的，而对于其他目标来讲可能是较差的。因此，存在一个折衷解的集合，称为Pareto最优解集（Pareto-optimal set）或非支配解集（non-dominated set）[1]。

自从Schaffer首次将矢量评价遗传算法VEGA[2]应用于MOPs求解以来，各种各样的多目标进化算法从传统的进化算法到成熟的最新技术都已被广泛应用到不同的领域中。基于算法所采用的选择机制，这些多目标进化算法可划分为以下三类：聚集函数法、基于群体的方法、基于Pareto的方法。聚集函数方法是将被优化的所有子目标聚集为单个目标，从而将多目标优化问题转化成单目标的优化问题。这种方法的最大困难在于怎样设置每个目标的权值；基于群体的方法主要依靠群体的进化来实现分别搜索，每一代进化时，依次针对每个子目标利用比例选择法产生r子群体，每个子群体大小为N/r（N为进化群体大小，r为子目标数），各子群体独立的执行进化操作，然后，再将r个子群体合并为一个群体大小为N的总群体，并执行进化操作。这种方法的缺点是对于一个好的折衷解，考虑了所有的子目标，但它对于单个子目标来说就不是最优解，这样的解在选择操作时可能会被“丢弃”。目前，大多数多目标进化算法归属于基于Pareto的方法，该方法的主要特征是在选择机制中融入了Pareto最优的概念，具有代表性的算法有 Niched Pareto Genetic Algorithm（NPGA）[3]、Nondominated Sorting Genetic Algorithm（NSGA）以及其改进版本 NSGA-II[4]，Pareto Envelope-based Selection Algorithm for Multiobjective Optimization（PESA）以及其改进版本 PESAII[5]，Strength Pareto Evolutionary Algorithm（SPEA）以及其改进版本SPEA2[6]。相关研究还可参看文献[7-9]。

在多目标进化算法的研究中，如何提升算法的收敛性和解集的多样性是算法设计的两个核心内容。在基于Pareto优化的多目标进化算法中，进化过程中每一代的主要工作就是构造非支配集以逐步地逼近Pareto前沿面，所以非支配集的构造是算法的重点。多目标进化的交叉、变异算子的参数，一般靠人为经验设置且固定不变，这不仅存在很大的偶然性而且对算法的收敛性和多样性都有影响。一些算法如NSGA-II采用的模拟二进制交叉算子SBX（Simulated Binary Crossover），对解空间搜索能力相对较弱，也一定程度上影响了算法的性能。

针对上面的问题，提出一种基于Pareto排序的混合多目标进化算法PHMOEA（HybridMulti-objective Evolutionary Algorithm Based on the Pareto Sort）。主要改进思想有以下几点：（1）在PHMOEA中，相入了干扰集（Interference Sets）用以刺激并优化非支配集的构造，从而改善解集的多样性和算法的收敛性；（2）在交叉算子中利用Pareto等级来自动调整相关参数，形成在交叉过程中的自适应运算并使得优秀个体基因尽可能的得到保留；（3）在变异操作中使用差分变异策略，并引入极端集（Extreme Set）中的个体来生成差异向量，从而提高解集的分布性。

2 Pareto多目标优化问题的相关定义

多目标优化问题又称为多标准优化问题。不失一般性，一个具有n个决策变量，m个目标变量的多目标优化问题可表述为：

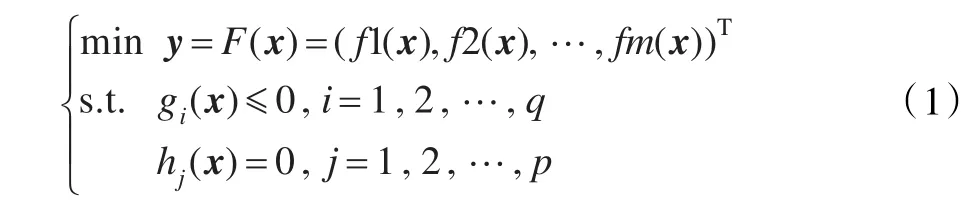
其中，x=(x1，x2，…，xn)∈X⊂Rn为n维的决策矢量，X为n维的决策空间，y=(y1，y2，…，ym)∈Y⊂Rm为m维的目标矢量，Y为m维的目标空间。目标函数F(x)定义了m个由决策空间向目标空间的的映射函数；gi(x)≤0，(i=1，2，…，q)定义了q个不等式的约束；hj(x)=0，(j=1，2，…，p)定义了p个等式约束。进一步，定义集合Ω={x|gi(x)≤0，hj(x)=0}为问题的可行域。在此基础上，给出以下几个重要定义。

定义1（Pareto支配）设f：Rn→Rm，xA，xB∈Ω⊆Rn。称个体xA支配个体xB当且仅当：

记作xA≻xB。

定义2（Pareto最优解）个体x*∈Ω被称为Pareto最优解（或非支配解），当且仅当满足以下条件：

定义3（Pareto最优解集）Pareto最优解集是所有Pareto最优解组成的集合，定义如下：

定义4（Pareto前沿面）Pareto最优解集P*中所有Pareto最优解对应的目标矢量组成的曲面称为Pareto前沿面PF*：

定义5（极端集）在多目标进化算法中，对于单个目标每代最优的点称之为极值点，所有目标的极值点集合称为极端集。

3 PHMOEA算法设计与描述

基于Pareto的多目标进化算法，是通过构造进化群体的非支配集，并使非支配集在进化过程中不断逼近真正的Pareto最优前沿面。一个进化群体的非支配集，实际上也是当前进化群体的最优个体集合。进化算法的每一次迭代，或每一代进化，都是为了构造更好的非支配集。在算法收敛之前，这样的非支配集是局部最优解集。由此可见，非支配集的好坏决定了进化算法的收敛性和多样性的好坏。本文通过设置一个外部干扰集，在进化过程中通过提高算法的搜索空间来达到不断影响并优化非支配集构造，从而提高算法的收敛性和解集的多样性。

多目标优化算法开始时，一般很难一下定位到最优解。所以，在算法初始阶段，越是难优化的问题越需要加强全局搜索能力，一旦定位到最优解的大致位置，越需要加强局部搜索能力，即加强精细的局部搜索。本文设计的交叉和变异操作都有一定自适应调整功能，较好地平衡了全局搜索与局部搜索。

3.1 种群的构造

在一般Pareto进化算法中，算法开始时随机产生一个初始群体Pt，在此基础上采用选择、交叉和变异操作产生一个新群体Qt，Pt和Qt的群体规模均为N，将Pt和Qt并入到大小为2N的Rt（初始t=0）中，然后根据Pareto排序从Rt选取个体进入Pt+1，直至Pt+1的规模为N。

图1 算法原始状态

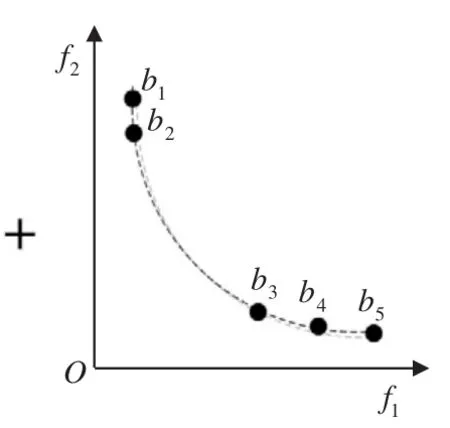
图2 干扰集产生

图3 干扰集的作用

3.2 交叉算子

针对二进制交叉算子SBX的缺点，本文采用算术交叉算法，一般以实数编码的交叉算子公式如下：

其中，λ为参数，在进化算法中一般根据经验设定，存在很大的偶然性。在精英保留机制的进化算法中，进化过程中的交叉运算中，都希望前一代较优的个体基因，在进化时尽可能得以保留；例如在公式（6）中，希望将前一代较优个体基因尽可能地保存在中。基于这一想法，本文重新定义了交叉算子的参数λ，让其与个体在群体中所处的等级相关联：

在计算运行初期，由于Pareto等级的关系，λ的变化较大，但随着进化的发展，种群中个体都趋向同一Pareto前沿面，λ趋于常值0.5，从而实现了交叉过程中的自适应调整。由于前一代较优个体基因被保留在中，所以在后面的变异操作中，将被赋予更大的概率进行变异操作。

3.3 变异算子

极值的引用会极大地提高算法的寻优效率[10]，变异操作在引用差分算法DE[11]的基础上，引用每代中的极值点并与所在Pareto等级相联系：

其中，xe，G为第G代极端集中的一个极值点，xe，G为G代种群中不等于xe，G的任意个体，n为xr1，G所在Pareto等级，m为种群中Pareto等级的最大值。

在算法的初期，种群分布区域较为宽广，个体差异较大，产生的差分向量 xe，G-xr1，G值较大，对个体xr1，G的扰动较大，从而实现算法的全局搜索。在进化的后期，种群的个体分布在最优解的附近，差分向量 xe，G-xr1，G的值较小，对个体xr1，G有微调作用，实现了算法的局部搜索。从整体上实现了变异算子的自适应操作。

为了检验极端值和差分变异的效果，将PHMOEA和NSGA-II算法在目标函数为2维的ZDT[12]测试函数上进行验证；设种群大小为100，迭代次数为50代，对比结果如图4所示。

在图4中，Ptrue即红线表示理论Pareto最优解。从图4中可以看出，PHMOEA算法的多样性明显好于NSGA-II，并且在收敛性上也强于NSGA-II。

在利用差分策略变异后，多目标进化算法存在这样一个问题：选择只在vi，G+1和xr1，G这两个个体比较支配关系后就做出取舍，显然这样的操作对MOEA来讲是不合适的，因为在MOEA中每个个体的优劣是和整个群体的状态相关的。为了避免上述问题，本文提出的选择操作将所有目标个体和由其产生的全部新个体一起构建一个新群体R。然后在群体R中，根据支配关系做出选择。

3.4 种群维护

基于Pareto排序的个体选择可以保证解沿着Pareto前沿进化，另一方面根据个体的拥挤距离的大小比较选择，可以使得群体的多样性、均匀性得到有效保护与维持。按照个体的密度估计方法[4]来评价每一个个体的拥挤距离度量，群体中每一个体i有两种可以比较的属性：

（1）非劣级别irank，irank表示个体i在种群中所在的Pareto等级，等级越小，个体越优。

（2）拥挤距离度量idistance，idistance表示个体i在种群中的聚集距离，距离越大被选中的可能性越大。

基于此，下面介绍具体的选择操作——拥挤二元锦标赛选择算子，在该算子中，个体i和j在联赛中获胜是基于下面的两个比较中的一个成立即可：

（1）个体i比j有比较好的非劣级别，即irank＜jrank。

图4 PHMOEA与NSGA-II在ZDT函数上50次迭代结果

（2）若i和j有相同的非劣级别，但i有较好的拥挤距离，即irank=jrank，且idistance＞jdistance。

3.5 算法主要流程

基于Pareto排序的混合多目标进化算法PHMOEA主要流程如下：

步骤1初始化大小为N的种群Pt和空的大小为2N+M的集合Rt（初始时t=0）（参见3.1节描述）。

步骤2从初始种群Pt中用二元锦标赛方法选取个体，进行交叉操作（根据公式（6）、（7））得到Pt(c)。

步骤3对Pt(c)中的个体采用公式（8）所述变异算子，进行变异操作，得到一个新群体Pt(c+m)，Pt和Pt(c+m)的群体规模均为N。

步骤4生成大小为M的干扰集ISt，将Pt、Pt(c+m)和ISt并入到Rt中，对Rt所有个体进行Pareto分层排序，并按Pareto等级从低到高并根据需要计算某个层次中的所有个体的拥挤距离依次进入Pt+1，直至Pt+1的规模为N。

步骤5若不满足终止条件，转步骤2。

步骤6否则，算法终止，现有种群即为所得Pareto最优解集。

4 性能测试实验与结果

为了验证PHMOEA算法在多目标优化问题上的求解性能，将其与NSGA-II和SPEA2算法在Schaffer[13]、Fonseca[14]、Kursawe[15]和 2 目标的 ZDT[12]、3 目标 DTLZ[16]测试函数集上进行实验对比。所有实验均在硬件配置为Intel®CoreTMCPU 2.80 GHz，内存4 GB的PC上进行。

参数设置如表1（n表示决策变量个数），其中PHMOEA中干扰集的大小设为15。

表1 算法参数值设置

算法性能对比采用通用的两个性能评价标准：

（1）Generational Distance[17]（GD）指标γ。γ测量算法最终获得的非支配解集Q与理论Pareto最优解近似集P*的逼近程度：

式中，di为Q中第i个体与P*之间在目标空间中的最小欧式距离；γ的值越小，说明算法获得的非支配解Q越接近真实的Pareto前沿，算法收敛性越好。

（2）Spread[17]度量指标 Δ。 Δ用来衡量算法最终获得的非支配解集Q中个体的分布均匀性及扩展程度：

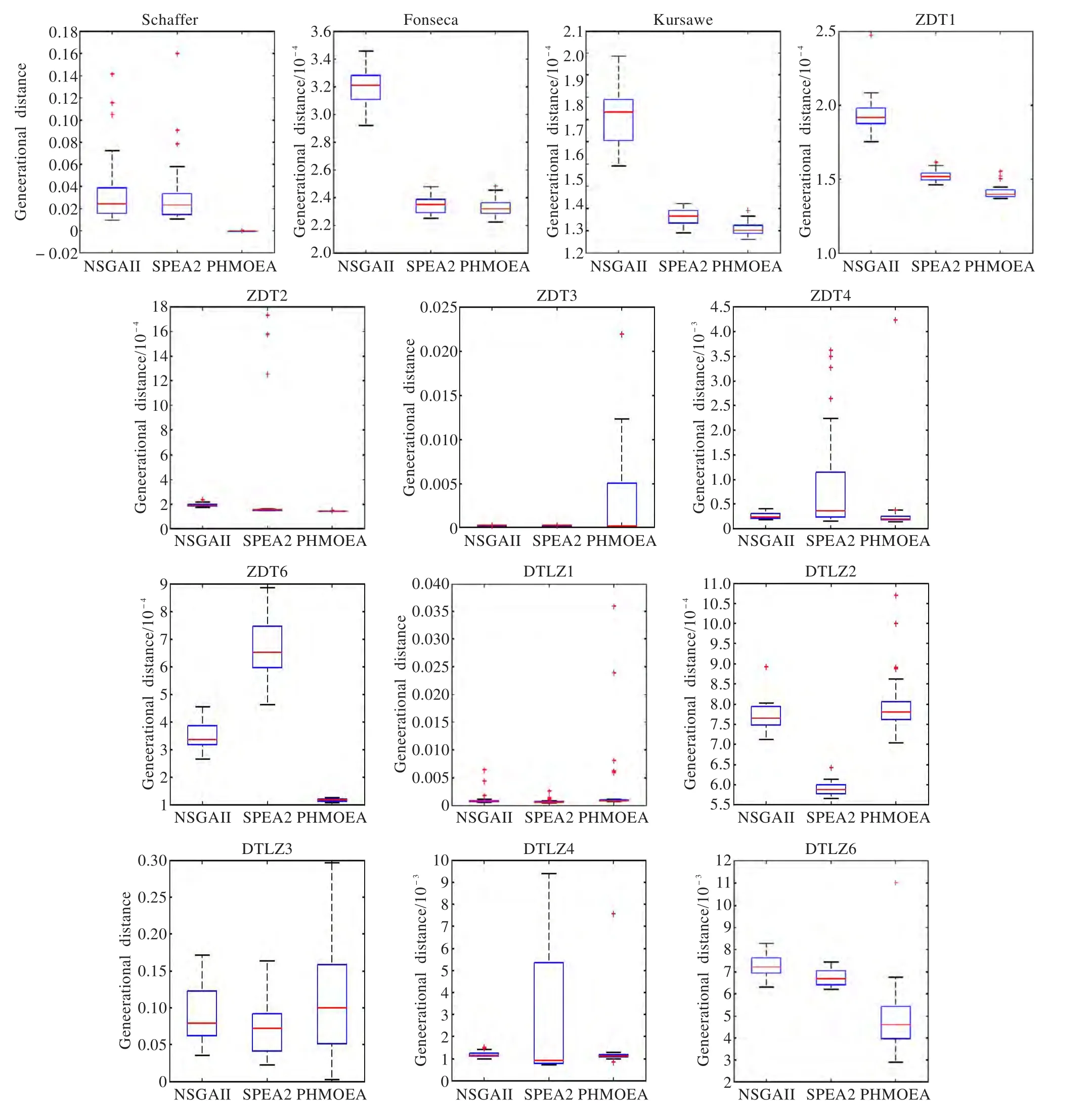
图5 NSGA-II、SPEA2和PHMOEA求解13个测试问题的GD指标的统计盒图

所有算法在各个测试函数上的初始种群大小NP均设置为100，迭代次数为250，交叉变异概率及其他指标同上。为了直观地看出算法对于各种测试问题的统计结果，利用盒图（boxplot）来统计数值。盒图是一种统计分析的重要工具，它可以很好地反应数据的统计分布情况。本文用该工具表现NSGA-II、SPEA2、PHMOEA这3种算法独立运行30次得到的解统计特性。其中，盒子的上下两条线分别表示样本的上下四分位数，盒子中间的水平线为样本的中位数，盒子上下的虚线表示样本的其余部分（野值除外），样本最大值为虚线顶端，样本最小值为虚线底端，“+”表示野值，盒子的切口为样本的置信区间。

从图5可以看出NSGA-II在ZDT3、DTLZ2和DTLZ3上的收敛性好于PHMOEA，在其他10个测试函数问题上PHMOEA收敛性均好于NSGA-II；而SPEA2在ZDT3、DTLZ1、DTLZ2和DTLZ3的收敛性较好，其他9个测试函数上PHMOEA效果较好。从图6中可以看出NSGA-II算法在DTLZ1、DTLZ2、和DTLZ6的多样性上较好，在其他10个测试函数上PHMOEA效果较好；SPEA2在DTLZ2、DTLZ4和DTLZ6多样性较好，在其他10个测试函数问题上PHMOEA效果较好。

在PHMOEA中，由于干扰集的加入，增加了Pareto排序的时间，但算法在交叉、变异操作上的时间效率较高，因此算法整体上的时间效率并不差。实验结果表明，PHMOEA在收敛性和多样性综合方面表现良好，与其他几种著名的算法相比有一定的优势。

5 结束语

在多目标进化算法的研究中，提升算法的收敛性和解集的多样性是算法设计的两个核心内容。本文提出一种基于Pareto排序的混合多目标进化算法PHMOEA，在Pareto排序的基础上，引入了干扰集以刺激并优化非支配集的构造，从而提高算法的收敛性和解集多样性，同时利用个体的Pareto等级和极端集改进了交叉和变异策略。通过和经典的NSGA-II和SPEA2算法在Schaffer、Fonseca、Kursawe和5个ZDT测试函数，5个DTLZ测试函数总共13个测试函数的实验结果对比和分析，说明了本文算法的有效性。

图6 NSGA-II、SPEA2和PHMOEA求解13个测试问题的Spread指标统计盒图

[1]Deb K.Multi-objective optimization using evolutionary algorithms[M].Chichester UK：Wiley，2001.

[2]Schaffer J D.Multiple objective optimization with vector evaluated genetic algorithms[C]//Proc of the Int’l Conf on Genetic Algorithms and their Application，1985：93-100.

[3]Horn J，Nafpliotis N，Goldberg D E.A niched Pareto genetic algorithm for multi-objective optimization[C]//Proc of the 1st IEEE Congress on Evolutionary Computation，1994：82-87.

[4]Deb K，Pratap A，Agarwal S，et al.A fast and elitist multiobjective genetic algorithm：NSGA-II[J].IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197.

[5]Corne D W，Knowles J D，Oates M J.PESA-II：regionbased selection in evolutionary multiobjective optimization[C]//Proc of the Genetic and Evolutionary Computation.SanFrancisco：MorganKaufmannPublisher，2001：283-290.

[6]Zitzler E L M，Thiele L.SPEA2：improving the strength pareto evolutionary algorithm[M]//Evolution Methods for Design，Optimization and Control with Applications to Industrial Problems.Berlin：Springer-Verlag，2002：95-100.

[7]公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究[J].软件学报，2009，20（2）：271-289.

[8]郑金华.多目标进化算法及其应用[M].北京：科学出版社，2010.

[9]刘鎏，李敏强.多目标优化进化算法及应用研究[D].天津：天津大学，2009.

[10]胡劲松，郑启伦.基于极值组合分析遗传算法之误[J].计算机学报，2003，26（12）：1759-1764.

[11]Storn R，Price K.Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11（4）：341-359.

[12]Zitzler E，Deb K，Thiele L.Comparison of multi-objective evolutionary：empirical results[J].Evolutionary Computation，2000，8（2）：173-195.

[13]Schaffer J D.Multi-objective optimization with vector evaluated genetic algorithms[C]//Proc of Int Conf on Genetic Algorithms and Their Applications，1985：93-100.

[14]Fonseca C M，Fleming P J.Multiobjective optimization and multiple constrant handling with evolutinary algorithms—Part II[J].IEEE Trans on Syst，Man：Cybern A，1998，28：38-47.

[15]Kursawe F.A variant of evolution stragies for vector optimization[M]//Parallel Problem Solving from Nature-PPSN.Berlin：Springer，1991：193-197.

[16]Deb K，Thiele L，Laumanns M，et al.Scalable test problems for evolutionary multiobjective optimization[M]//Evolutionary Multiobjective Optimization，Theoretical Advance and Applications.Berlin Germany：Springer-Verlag，2005：825-830.

[17]Lixin T，Xianpeng W.A hybrid multiobjective evolutionary algorithm formultiobjective optimization problems[J].IEEE Transactions on Evolutionary Computation，2013，17（1）：20-45.